В геометрии двенадцатиугольником ( двенадцатиугольником ) называется любой двенадцатиугольник .

Правильный двенадцатиугольник — это фигура со сторонами одинаковой длины и внутренними углами одинакового размера. Он имеет двенадцать линий отражательной симметрии и вращательную симметрию порядка 12. Правильный двенадцатиугольник представлен символом Шлефли {12} и может быть построен как усеченный шестиугольник , t{6}, или дважды усеченный треугольник , tt{3}. Внутренний угол при каждой вершине правильного двенадцатиугольника равен 150°.
Площадь правильного двенадцатиугольника со стороной длиной a определяется по формуле:
А в терминах апофемы r (см. также вписанную фигуру ) площадь равна:
В терминах радиуса описанной окружности R площадь равна: [1]
Размах S додекагона — это расстояние между двумя параллельными сторонами, равное удвоенной апофеме. Простая формула для площади (при заданной длине стороны и размахе):
Это можно проверить с помощью тригонометрического соотношения:
Периметр правильного двенадцатиугольника через радиус описанной окружности равен: [2]
Периметр в терминах апофемы равен:
Этот коэффициент в два раза больше коэффициента, найденного в уравнении апофемы для площади. [3]
Так как 12 = 2 2 × 3, то правильный двенадцатиугольник можно построить с помощью циркуля и линейки :

Коксетер утверждает, что каждый зоногон (2- метровый угольник, противоположные стороны которого параллельны и имеют одинаковую длину) можно разбить на m ( m -1)/2 параллелограммов. [4] В частности, это верно для правильных многоугольников с равным числом сторон, в этом случае все параллелограммы являются ромбами. Для правильного додекагона m = 6, и его можно разделить на 15: 3 квадрата, 6 широких ромбов с углом 30° и 6 узких ромбов с углом 15°. Это разложение основано на проекции многоугольника Петри 6-куба с 15 из 240 граней. Последовательность OEIS A006245 определяет число решений как 908, включая до 12-кратные вращения и хиральные формы в отражении.
Одним из способов использования блоков математических манипулятивных шаблонов является создание ряда различных двенадцатиугольников. [5] Они связаны с ромбическими разрезами, когда 3 ромба по 60° объединены в шестиугольники, полушестиугольные трапеции или разделены на 2 равносторонних треугольника.
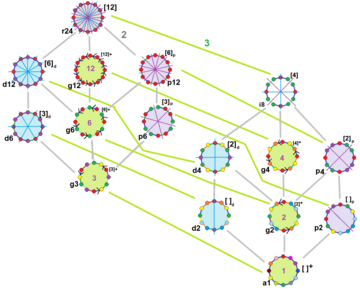
Правильный додекагон имеет симметрию Dih 12 , порядок 24. Существует 15 различных подгрупп диэдральных и циклических симметрий. Каждая подгруппа симметрии допускает одну или несколько степеней свободы для неправильных форм. Только подгруппа g12 не имеет степеней свободы, но может рассматриваться как направленные ребра .
Правильный двенадцатиугольник может заполнить вершину плоскости другими правильными многоугольниками четырьмя способами:
Вот три примера периодических плоских мозаик , которые используют правильные двенадцатиугольники, определяемые конфигурацией их вершин :
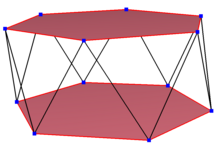
Косой додекагон — это косой многоугольник с 12 вершинами и ребрами, но не лежащий на одной плоскости. Внутренность такого додекагона обычно не определена. Косой зигзагообразный додекагон имеет вершины, чередующиеся между двумя параллельными плоскостями.
Правильный косой додекагон является вершинно-транзитивным с равными длинами сторон. В 3-мерном пространстве это будет зигзагообразный косой додекагон, который можно увидеть в вершинах и боковых ребрах шестиугольной антипризмы с той же симметрией D 5d , [2 + ,10], порядок 20. Додекаграммическая антипризма, s{2,24/5} и додекаграммическая скрещенная антипризма, s{2,24/7} также имеют правильные косые додекагоны.
Правильный додекагон является многоугольником Петри для многих многогранников более высокой размерности, рассматриваемых как ортогональные проекции на плоскости Коксетера . Примерами в 4 измерениях являются 24-ячейник , плосконосый 24-ячейник , 6-6 дуопризма , 6-6 дуопирамида . В 6 измерениях 6-куб , 6-ортоплекс , 2 21 , 1 22 . Это также многоугольник Петри для большого 120-ячейника и большого звёздчатого 120-ячейника .
Додекаграмма — это 12-сторонний звездчатый многоугольник, представленный символом {12/n}. Существует один правильный звездчатый многоугольник : {12/5}, использующий те же вершины, но соединяющий каждую пятую точку. Существуют также три соединения: {12/2} сокращается до 2{6} как два шестиугольника , а {12/3} сокращается до 3{4} как три квадрата , {12/4} сокращается до 4{3} как четыре треугольника, а {12/6} сокращается до 6{2} как шесть вырожденных двуугольников .
Более глубокие усечения правильного додекагона и додекаграмм могут производить изогональные ( вершинно-транзитивные ) промежуточные формы звездчатого многоугольника с равноотстоящими вершинами и двумя длинами ребер. Усеченный шестиугольник является додекагоном, t{6}={12}. Квазиусеченный шестиугольник, перевернутый как {6/5}, является додекаграммой: t{6/5}={12/5}. [7]
В печатных заглавных буквах буквы E , H и X (и I в шрифте с засечками ) имеют двенадцатиугольные очертания. Крест — это двенадцатиугольник, как и логотип автомобильного подразделения Chevrolet .

Правильный двенадцатиугольник занимает видное место во многих зданиях. Torre del Oro — двенадцатиугольная военная сторожевая башня в Севилье , на юге Испании , построенная династией Альмохадов . Церковь Вера-Крус начала тринадцатого века в Сеговии , Испания, имеет двенадцатиугольную форму. Другим примером являются Порта ди Венере (Ворота Венеры) в Спелло , Италия , построенные в I веке до нашей эры, с двумя двенадцатиугольными башнями, называемыми «Башнями Проперция».

К обычным двенадцатиугольным монетам относятся: