ползать по мостовой

Механизм деформации кристаллического твердого тела

Диаграмма, показывающая, как атомы и вакансии перемещаются через зерно в рамках механизма ползучести Кобла.

В материаловедении ползучесть Кобла , форма диффузионной ползучести , является механизмом деформации кристаллических твердых тел. В отличие от других механизмов диффузионной ползучести, ползучесть Кобла похожа на ползучесть Набарро-Херринга тем, что она доминирует при более низких уровнях напряжения и более высоких температурах, чем механизмы ползучести, использующие скольжение дислокаций . ^[1] Ползучесть Кобла происходит посредством диффузии атомов в материале вдоль границ зерен . Этот механизм наблюдается в поликристаллах или вдоль поверхности в монокристалле , что создает чистый поток материала и скольжение границ зерен.

Американский ученый-материаловед Роберт Л. Кобл впервые изложил свою теорию о том, как материалы ползут через границы зерен и при высоких температурах в оксиде алюминия . Здесь он, как известно, заметил другой механизм ползучести, который больше зависел от размера зерна. ^[2]

Скорость деформации материала, испытывающего ползучесть по Коблу, определяется по формуле: $${\displaystyle {\begin{aligned}{\frac {d\varepsilon _{C}}{dt}}\equiv {\dot {\varepsilon }}_{C}&=A_{C}{\frac {\delta '}{d^{3}}}{\frac {\sigma \Omega }{k_{\rm {B}}T}}D_{0}\exp \left(-{\frac {Q_{f}+Q_{m}}{k_{\rm {B}}T}}\right)\\[4pt]&=A_{C}{\frac {\delta '}{d^{3}}}{\frac {\sigma \Omega }{k_{\rm {B}}T}}D_{\rm {GB}}\end{aligned}}}$$

${\displaystyle A_{c}}$является геометрическим префактором

${\displaystyle \sigma }$это приложенное напряжение,

${\displaystyle d}$средний диаметр зерна,

${\displaystyle \delta '}$ширина границы зерна,

${\displaystyle D_{\rm {GB}}=D_{0}\exp \left(-{\tfrac {Q_{f}\,+\,Q_{m}}{k_{\rm {B}}T}}\right)}$ - коэффициент диффузии в границах зерен,

${\displaystyle Q_{f}}$- энергия образования вакансии ,

${\displaystyle Q_{m}}$это энергия активации диффузии вдоль границы зерна

${\displaystyle k_{\rm {B}}}$постоянная Больцмана ,

${\displaystyle T}$это термодинамическая температура (в кельвинах )

${\displaystyle \Omega }$атомный объем материала.

Вывод

Ползучесть ковша, диффузионный механизм, управляется градиентом концентрации вакансий (или масс). Изменение концентрации вакансий от ее равновесного значения определяется как ${\displaystyle \Delta C}$ ${\displaystyle C_{0}}$

${\displaystyle \Delta C=C_{0}{\frac {\sigma \Omega }{kT}}}$

Это можно увидеть, заметив, что и взяв высокотемпературное расширение, где первый член в правой части - это концентрация вакансий от растягивающего напряжения, а второй член - это концентрация из-за сжимающего напряжения. Это изменение концентрации происходит перпендикулярно к оси приложенного напряжения, в то время как параллельно напряжению нет никаких изменений в концентрации вакансий (из-за того, что разрешенное напряжение и работа равны нулю). ^[2] ${\displaystyle \Delta C\propto C_{0}e^{\sigma \Omega /kT}-C_{0}e^{-\sigma \Omega /kT}}$

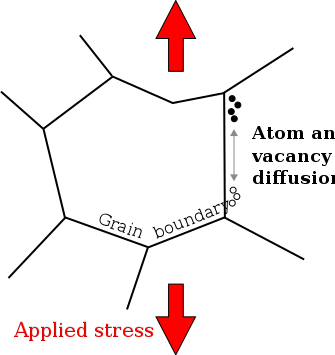
Продолжаем, предполагая, что зерно сферическое, чтобы соответствовать выводу для ползучести Набарро–Херринга ; однако мы включим геометрические константы в константу пропорциональности . Если мы рассмотрим концентрацию вакансий поперек зерна под приложенным растягивающим напряжением, то заметим, что на экваторе (перпендикулярно приложенному напряжению) концентрация вакансий больше, чем на полюсах (параллельно приложенному напряжению). Следовательно, между полюсами и экватором зерна существует поток вакансий. Поток вакансий определяется первым законом Фика на границе: коэффициент диффузии , умноженный на градиент концентрации вакансий. Для градиента мы берем среднее значение, заданное как , где мы разделили общую разницу концентраций на длину дуги между экватором и полюсом, а затем умножаем на ширину и длину границы . ${\displaystyle A}$ ${\displaystyle D_{v}}$ ${\displaystyle \Delta C/(\pi R/2)}$ ${\displaystyle \delta '}$ ${\displaystyle 2\pi R}$

${\displaystyle J_{v}=A'D_{v}{\frac {\Delta C}{\pi R/2}}\delta '(2\pi R)}$

где - константа пропорциональности. Отсюда следует, что изменение объема из-за потока вакансий, диффундирующих из источника площадью, равно потоку вакансий, умноженному на атомный объем : ${\displaystyle A'}$ ${\displaystyle \pi R^{2}dR/dt}$ ${\displaystyle \pi R^{2}}$ ${\displaystyle J_{v}}$ ${\displaystyle \Omega }$

${\displaystyle J_{v}\Omega =\pi R^{2}dR/dt=\pi R^{3}{\dot {\epsilon }}}$

где второе равенство следует из определения скорости деформации: . Отсюда можно определить скорость деформации: ${\displaystyle {\dot {\epsilon }}=(1/R)(dR/dt)}$

${\displaystyle {\dot {\epsilon }}_{C}={\frac {J_{v}\Omega }{\pi R^{3}}}=AD_{v}\Delta C\Omega {\frac {\delta '}{R^{3}}}=AD_{GB}{\frac {\sigma \Omega }{kT}}{\frac {\delta '}{R^{3}}}}$

где имеет поглощенные константы и коэффициент диффузии вакансий через границу зерна . ${\displaystyle A'\rightarrow A}$ ${\displaystyle D_{GB}=D_{v}C_{0}\Omega }$

Сравнение с другими механизмами ползучести

Набарро–Селедка

Ползучесть Кобла и ползучесть Набарро–Херринга являются тесно связанными механизмами. Оба они являются диффузионными процессами, движущимися одним и тем же градиентом концентрации вакансий, происходят в условиях высокой температуры и низкого напряжения, и их производные схожи. ^[1] Для обоих механизмов скорость деформации линейно пропорциональна приложенному напряжению , и существует экспоненциальная зависимость от температуры. Разница в том, что при ползучести Кобла массоперенос происходит вдоль границ зерен, тогда как при ползучести Набарро–Херринга диффузия происходит через кристалл. Из-за этого ползучесть Набарро–Херринга не зависит от толщины границ зерен и имеет более слабую зависимость от размера зерна . При ползучести Набарро–Херринга скорость деформации пропорциональна в отличие от зависимости для ползучести Кобла. При рассмотрении чистой скорости диффузионной ползучести сумма обеих скоростей диффузии имеет решающее значение, поскольку они работают в параллельных процессах. ${\displaystyle {\dot {\epsilon }}}$ ${\displaystyle \sigma }$ ${\displaystyle d}$ ${\displaystyle d^{-2}}$ ${\displaystyle d^{-3}}$

Энергия активации для ползучести Набарро-Херринга, в общем, отличается от ползучести Кобла. Это можно использовать для определения того, какой механизм является доминирующим. Например, энергия активации для переползания дислокации такая же, как для Набарро-Херринга, поэтому, сравнивая температурную зависимость режимов низкого и высокого напряжения, можно определить, является ли доминирующей ползучесть Кобла или ползучесть Набарро-Херринга. ^[3]

Исследователи обычно используют эти соотношения для определения того, какой механизм доминирует в материале; изменяя размер зерна и измеряя, как это влияет на скорость деформации, они могут определить значение in и сделать вывод о том, какой механизм ползучести — Кобла или Набарро–Херринга — является доминирующим. ^[4] ${\displaystyle n}$ ${\displaystyle {\dot {\epsilon }}~\alpha ~d^{n}}$

Ползучесть дислокаций

При умеренном и высоком напряжении доминирующий механизм ползучести больше не является линейным по приложенному напряжению . Ползучесть дислокаций, иногда называемая степенным законом ползучести (PLC), имеет степенную зависимость от приложенного напряжения в диапазоне от 3 до 8. ^[1] Движение дислокаций связано с атомной и решеточной структурой кристалла, поэтому разные материалы по-разному реагируют на напряжение, в отличие от ползучести по Коблу, которая всегда линейна. Это позволяет легко идентифицировать два механизма, найдя наклон vs . ${\displaystyle \sigma }$ ${\displaystyle \log {\dot {\epsilon }}}$ ${\displaystyle \log {\sigma }}$

Подъем-скольжение дислокаций и ползучесть Кобла вызывают скольжение по границам зерен . ^[1]

Карты механизма деформации

Чтобы понять температурные и стрессовые режимы, в которых ползучесть по Коблу доминирует для материала, полезно взглянуть на карты механизмов деформации. Эти карты отображают нормализованное напряжение в зависимости от нормализованной температуры и разграничивают, где конкретные механизмы ползучести доминируют для данного материала и размера зерна (некоторые карты имитируют 3-ю ось, чтобы показать размер зерна). Эти карты следует использовать только в качестве руководства, поскольку они основаны на эвристических уравнениях. ^[1] Эти карты полезны для определения механизма ползучести, когда известны рабочие напряжения и температура для применения, чтобы направлять проектирование материала.

Скольжение по границам зерен

Поскольку ползучесть Coble подразумевает массовый перенос вдоль границ зерен, без надлежащего размещения внутри материала будут образовываться трещины или пустоты. Скольжение по границам зерен — это процесс, при котором зерна перемещаются, чтобы предотвратить разделение на границах зерен. ^[1] Этот процесс обычно происходит во временных масштабах, значительно превышающих диффузию масс (на порядок быстрее). Из-за этого скорость скольжения по границам зерен обычно не имеет значения для определения материальных процессов. Однако некоторые границы зерен, такие как когерентные границы или там, где структурные особенности препятствуют движению границ зерен, могут замедлить скорость скольжения по границам зерен до точки, когда это необходимо учитывать. Процессы, лежащие в основе скольжения по границам зерен, те же самые, что и те, которые вызывают диффузионную ползучесть ^[1]

Этот механизм был первоначально предложен Эшби и Верраллом в 1973 году как ползучесть с переключением зерен. ^[5] Он конкурирует с ползучестью Кобла; однако переключение зерен будет доминировать при больших напряжениях, в то время как ползучесть Кобла будет доминировать при низких напряжениях.

Эта модель предсказывает скорость деформации с пороговой деформацией для переключения зерен . ^[1] ${\displaystyle 0.72\gamma /d}$

${\displaystyle {\dot {\epsilon }}_{GS}\propto {\frac {\Omega }{kT}}{\frac {\delta 'D_{GB}}{d^{3}}}(\sigma -{\frac {0.72\gamma }{d}})}$

Связь с ползучестью по Коблу становится ясной, если рассмотреть первый член, который зависит от толщины границ зерен и обратного размера зерна в кубе . ${\displaystyle \delta '}$ ${\displaystyle d^{-3}}$

Ссылки

1. Кортни, Томас (2000). Механическое поведение материалов . стр. 293-353.
2. Coble, Robert L. (15 октября 1962 г.). «Модель ползучести, контролируемой граничной диффузией, в поликристаллических материалах». Журнал прикладной физики . 34 (6): 1679–1682. doi :10.1063/1.1702656.
3. "MIT OCW 3.22 Механические свойства материалов. Весна 2008. PSET 5. Решения" (PDF) .
4. Мейерс, Марк Андре; Чавла, Кришан Кумар (2008). Механическое поведение материалов . Издательство Кембриджского университета. С. 555–557.
5. MF Ashby, RA Verrall, Диффузионно-аккомодированное течение и сверхпластичность, Acta Metall. 21 (1973) 149–163, https://doi.org/10.1016/0001-6160(73)90057-6