Диффузия

Перенос растворенных веществ из области с самой высокой концентрацией в область с самой низкой концентрацией

Некоторые частицы растворяются в стакане воды. Сначала все частицы находятся около одного верхнего угла стакана. Если частицы беспорядочно перемещаются («диффузируются») в воде, они в конечном итоге распределяются беспорядочно и равномерно из области высокой концентрации в область низкой и организуются (диффузия продолжается, но без чистого потока ).

Покадровая съемка диффузии красителя, растворенного в воде, в гель.

Диффузия с микроскопической и макроскопической точек зрения. Первоначально молекулы растворенного вещества находятся слева от барьера (фиолетовая линия), а справа их нет. Барьер удаляется, и растворенное вещество диффундирует, заполняя весь контейнер. Вверху: Одна молекула движется хаотично. В середине: При большем количестве молекул наблюдается статистическая тенденция, что растворенное вещество заполняет контейнер все более и более равномерно. Внизу: При огромном количестве молекул растворенного вещества вся хаотичность исчезает: растворенное вещество, по-видимому, движется плавно и детерминированно из областей с высокой концентрацией в области с низкой концентрацией. Микроскопической силы, толкающей молекулы вправо, нет , но она , по-видимому, есть на нижней панели. Эта кажущаяся сила называется энтропийной силой .

Трехмерная визуализация диффузии фиолетового красителя в воде.

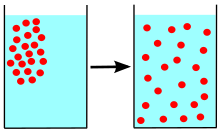
Диффузия — это чистое перемещение чего-либо (например, атомов, ионов, молекул, энергии), как правило, из области с более высокой концентрацией в область с более низкой концентрацией. Диффузия обусловлена ​​градиентом свободной энергии Гиббса или химического потенциала . Возможна диффузия «вверх» из области с более низкой концентрацией в область с более высокой концентрацией, как при спинодальном разложении . Диффузия — это стохастический процесс из-за присущей диффундирующей сущности случайности и может использоваться для моделирования многих реальных стохастических сценариев. Поэтому диффузия и соответствующие математические модели используются в нескольких областях за пределами физики, таких как статистика , теория вероятностей , теория информации , нейронные сети , финансы и маркетинг .

Концепция диффузии широко используется во многих областях, включая физику ( диффузия частиц ), химию , биологию , социологию , экономику , статистику , науку о данных и финансы (диффузия людей, идей, данных и ценовых значений). Однако центральная идея диффузии является общей для всех них: вещество или совокупность, подвергающиеся диффузии, распространяются из точки или места, в котором наблюдается более высокая концентрация этого вещества или совокупности.

Градиент — это изменение значения величины; например, концентрации, давления или температуры с изменением другой переменной, обычно расстояния . Изменение концентрации на расстоянии называется градиентом концентрации , изменение давления на расстоянии называется градиентом давления , а изменение температуры на расстоянии называется градиентом температуры .

Слово «диффузия» происходит от латинского слова diffundere , что означает «распространяться».

Отличительной чертой диффузии является то, что она зависит от случайного блуждания частиц и приводит к смешиванию или переносу масс без необходимости направленного объемного движения. Объемное движение, или объемный поток, является характеристикой адвекции . ^[1] Термин конвекция используется для описания комбинации обоих явлений переноса .

Если процесс диффузии можно описать законами Фика , то он называется нормальной диффузией (или фиковской диффузией); в противном случае он называется аномальной диффузией (или нефиковской диффузией).

При рассмотрении степени диффузии используются две шкалы длины в двух различных сценариях:

1. Броуновское движение импульсивного точечного источника (например, одиночного распыления духов) — квадратный корень из среднего квадрата смещения от этой точки. В фикковской диффузии это , где — размерность этого броуновского движения; ${\displaystyle {\sqrt {2nDt}}}$ ${\displaystyle n}$
2. Постоянный источник концентрации в одном измерении — длина диффузии. В фикковской диффузии это . ${\displaystyle 2{\sqrt {Dt}}}$

Диффузия против объемного потока

«Объемный поток» — это движение/поток всего тела из-за градиента давления (например, вода, вытекающая из крана). «Диффузия» — это постепенное движение/рассеивание концентрации внутри тела без чистого движения материи. Примером процесса, в котором происходит как объемное движение , так и диффузия, является человеческое дыхание. ^[2]

Во-первых, происходит процесс «объемного потока». Легкие расположены в грудной полости , которая расширяется как первый шаг внешнего дыхания. Это расширение приводит к увеличению объема альвеол в легких, что вызывает снижение давления в альвеолах. Это создает градиент давления между воздухом снаружи тела при относительно высоком давлении и альвеолами при относительно низком давлении. Воздух движется вниз по градиенту давления через дыхательные пути легких и в альвеолы ​​до тех пор, пока давление воздуха и давление в альвеолах не станут равными, то есть движение воздуха объемным потоком прекращается, как только больше нет градиента давления.

Во-вторых, происходит процесс «диффузии». Воздух, поступающий в альвеолы, имеет более высокую концентрацию кислорода, чем «застоявшийся» воздух в альвеолах. Увеличение концентрации кислорода создает градиент концентрации кислорода между воздухом в альвеолах и кровью в капиллярах, которые окружают альвеолы. Затем кислород перемещается путем диффузии вниз по градиенту концентрации в кровь. Другим следствием поступления воздуха в альвеолы ​​является то, что концентрация углекислого газа в альвеолах уменьшается. Это создает градиент концентрации для углекислого газа, чтобы диффундировать из крови в альвеолы, так как свежий воздух имеет очень низкую концентрацию углекислого газа по сравнению с кровью в организме.

В-третьих, есть еще один процесс «объемного потока». Затем насосное действие сердца перекачивает кровь по всему телу. Когда левый желудочек сердца сокращается, объем уменьшается, что увеличивает давление в желудочке. Это создает градиент давления между сердцем и капиллярами, и кровь движется по кровеносным сосудам объемным потоком вниз по градиенту давления.

Распространение в контексте различных дисциплин

Диффузионные печи, используемые для термического окисления

Существует два способа ввести понятие диффузии : либо феноменологический подход, начинающийся с законов диффузии Фика и их математических следствий, либо физический и атомистический подход, рассматривающий случайное блуждание диффундирующих частиц . ^[3]

В феноменологическом подходе диффузия — это перемещение вещества из области высокой концентрации в область низкой концентрации без объемного движения . Согласно законам Фика, поток диффузии пропорционален отрицательному градиенту концентраций. Он идет из областей более высокой концентрации в области более низкой концентрации. Некоторое время спустя были разработаны различные обобщения законов Фика в рамках термодинамики и неравновесной термодинамики . ^[4]

С атомистической точки зрения диффузия рассматривается как результат случайного блуждания диффундирующих частиц. При молекулярной диффузии движущиеся молекулы в газе, жидкости или твердом теле самодвижутся под действием кинетической энергии. Случайное блуждание мелких частиц во взвешенном состоянии в жидкости было открыто в 1827 году Робертом Брауном , который обнаружил, что мельчайшие частицы, взвешенные в жидкой среде и достаточно большие, чтобы быть видимыми под оптическим микроскопом, демонстрируют быстрое и непрерывное нерегулярное движение частиц, известное как броуновское движение. Теория броуновского движения и атомистические основы диффузии были разработаны Альбертом Эйнштейном . ^[5] Понятие диффузии обычно применяется к любому предмету, включающему случайные блуждания в ансамблях индивидуумов.

В химии и материаловедении диффузия также относится к движению молекул жидкости в пористых твердых телах. ^[6] В пористых твердых телах различают различные типы диффузии. Молекулярная диффузия происходит, когда столкновение с другой молекулой более вероятно, чем столкновение со стенками пор. В таких условиях коэффициент диффузии аналогичен коэффициенту диффузии в незамкнутом пространстве и пропорционален средней длине свободного пробега. Диффузия Кнудсена происходит, когда диаметр поры сопоставим или меньше средней длины свободного пробега диффундирующей через пору молекулы. При этом условии столкновение со стенками пор постепенно становится более вероятным, а коэффициент диффузии ниже. Наконец, существует конфигурационная диффузия, которая происходит, если молекулы имеют сопоставимый размер с размером поры. При этом условии коэффициент диффузии намного ниже по сравнению с молекулярной диффузией, и небольшие различия в кинетическом диаметре молекулы вызывают большие различия в коэффициенте диффузии .

Биологи часто используют термины «чистое движение» или «чистая диффузия» для описания движения ионов или молекул путем диффузии. Например, кислород может диффундировать через клеточные мембраны, пока за пределами клетки сохраняется более высокая концентрация кислорода. Однако, поскольку движение молекул является случайным, иногда молекулы кислорода выходят из клетки (против градиента концентрации). Поскольку за пределами клетки находится больше молекул кислорода, вероятность того , что молекулы кислорода войдут в клетку, выше, чем вероятность того, что молекулы кислорода покинут клетку. Следовательно, «чистое» движение молекул кислорода (разница между числом молекул, входящих в клетку или выходящих из нее) происходит в клетку. Другими словами, происходит чистое движение молекул кислорода вниз по градиенту концентрации.

История диффузии в физике

В рамках времени диффузия в твердых телах использовалась задолго до создания теории диффузии. Например, Плиний Старший ранее описал процесс цементации , который производит сталь из элемента железа (Fe) посредством диффузии углерода. Другой пример хорошо известен на протяжении многих столетий, диффузия цветов витражного стекла или фаянса и китайской керамики .

В современной науке первое систематическое экспериментальное исследование диффузии было проведено Томасом Грэхемом . Он изучал диффузию в газах, и основное явление было описано им в 1831–1833 годах: ^[7]

«...газы различной природы, когда они соприкасаются, не располагаются в соответствии со своей плотностью, наиболее тяжелые внизу, а более легкие наверху, но они самопроизвольно диффундируют, взаимно и равномерно, друг через друга и таким образом остаются в тесном состоянии смеси в течение любого промежутка времени».

Измерения Грэхема способствовали выводу Джеймсом Клерком Максвеллом в 1867 году коэффициента диффузии CO2 _в воздухе. Погрешность составляет менее 5%.

В 1855 году Адольф Фик , 26-летний демонстратор анатомии из Цюриха, предложил свой закон диффузии . Он использовал исследования Грэхема, заявив, что его цель — «разработка фундаментального закона для операции диффузии в одном элементе пространства». Он утверждал глубокую аналогию между диффузией и проводимостью тепла или электричества, создав формализм, аналогичный закону Фурье для теплопроводности (1822) и закону Ома для электрического тока (1827).

Роберт Бойль продемонстрировал диффузию в твердых телах в 17 веке ^[8] путем проникновения цинка в медную монету. Тем не менее, диффузия в твердых телах не изучалась систематически до второй половины 19 века. Уильям Чандлер Робертс-Остин , известный британский металлург и бывший помощник Томаса Грэхема, систематически изучал диффузию в твердом состоянии на примере золота в свинце в 1896 году. : ^[9]

«... Моя давняя связь с исследованиями Грэма сделала для меня почти долгом попытаться распространить его работу по диффузии жидкостей на металлы».

В 1858 году Рудольф Клаузиус ввел понятие средней длины свободного пробега . В том же году Джеймс Клерк Максвелл разработал первую атомистическую теорию процессов переноса в газах. Современная атомистическая теория диффузии и броуновского движения была разработана Альбертом Эйнштейном , Марианом Смолуховским и Жаном-Батистом Перреном . Людвиг Больцман , развивая атомистические основы макроскопических процессов переноса , ввел уравнение Больцмана , которое служило математикам и физикам источником идей и проблем процессов переноса на протяжении более 140 лет. ^[10]

В 1920–1921 годах Дьёрдь де Хевеши измерил самодиффузию с помощью радиоизотопов . Он изучал самодиффузию радиоактивных изотопов свинца в жидком и твердом свинце.

Яков Френкель (иногда Яков/Якоб Френкель) предложил и развил в 1926 году идею диффузии в кристаллах через локальные дефекты (вакансии и межузельные атомы). Он пришел к выводу, что процесс диффузии в конденсированных средах представляет собой совокупность элементарных скачков и квазихимических взаимодействий частиц и дефектов. Он ввел несколько механизмов диффузии и нашел константы скорости из экспериментальных данных.

Некоторое время спустя Карл Вагнер и Вальтер Х. Шоттки развили идеи Френкеля о механизмах диффузии. В настоящее время общепризнано, что атомные дефекты необходимы для опосредования диффузии в кристаллах. ^[9]

Генри Эйринг с соавторами применил свою теорию абсолютных скоростей реакции к квазихимической модели диффузии Френкеля. ^[11] Аналогия между кинетикой реакции и диффузией приводит к различным нелинейным версиям закона Фика. ^[12]

Базовые модели диффузии

Определение диффузионного потока

Каждая модель диффузии выражает поток диффузии с использованием концентраций, плотностей и их производных. Поток — это вектор , представляющий количество и направление переноса. При наличии небольшой площади с нормалью перенос физической величины через площадь за время равен ${\displaystyle \mathbf {J} }$ ${\displaystyle \Delta S}$ ${\displaystyle {\boldsymbol {\nu }}}$ ${\displaystyle N}$ ${\displaystyle \Delta S}$ ${\displaystyle \Delta t}$

${\displaystyle \Delta N=(\mathbf {J} ,{\boldsymbol {\nu }})\,\Delta S\,\Delta t+o(\Delta S\,\Delta t)\,,}$

где — внутренний продукт , а — обозначение с маленькой буквой «о» . Если мы используем обозначение векторной площади , то ${\displaystyle (\mathbf {J} ,{\boldsymbol {\nu }})}$ ${\displaystyle o(\cdots )}$ ${\displaystyle \Delta \mathbf {S} ={\boldsymbol {\nu }}\,\Delta S}$

${\displaystyle \Delta N=(\mathbf {J} ,\Delta \mathbf {S} )\,\Delta t+o(\Delta \mathbf {S} \,\Delta t)\,.}$

Размерность диффузионного потока равна [поток] = [количество]/([время]·[площадь]). Диффундирующей физической величиной может быть число частиц, масса, энергия, электрический заряд или любая другая скалярная экстенсивная величина . Для ее плотности, , уравнение диффузии имеет вид ${\displaystyle N}$ ${\displaystyle n}$

${\displaystyle {\frac {\partial n}{\partial t}}=-\nabla \cdot \mathbf {J} +W\,,}$

где - интенсивность любого локального источника этой величины (например, скорость химической реакции). Для уравнения диффузии граничные условия отсутствия потока можно сформулировать как на границе, где - нормаль к границе в точке . ${\displaystyle W}$ ${\displaystyle (\mathbf {J} (x),{\boldsymbol {\nu }}(x))=0}$ ${\displaystyle {\boldsymbol {\nu }}}$ ${\displaystyle x}$

Нормальный градиент концентрации одного компонента

Первый закон Фика: Диффузионный поток, , пропорционален отрицательному градиенту пространственной концентрации, : ${\displaystyle \mathbf {J} }$ ${\displaystyle n(x,t)}$

${\displaystyle \mathbf {J} =-D(x)\,\nabla n(x,t),}$

где D — коэффициент диффузии . Соответствующее уравнение диффузии (второй закон Фика) имеет вид

${\displaystyle {\frac {\partial n(x,t)}{\partial t}}=\nabla \cdot (D(x)\,\nabla n(x,t))\,.}$

В случае, если коэффициент диффузии не зависит от , второй закон Фика можно упростить до ${\displaystyle x}$

${\displaystyle {\frac {\partial n(x,t)}{\partial t}}=D\,\Delta n(x,t)\ ,}$

где оператор Лапласа , ${\displaystyle \Delta }$

${\displaystyle \Delta n(x,t)=\sum _{i}{\frac {\partial ^{2}n(x,t)}{\partial x_{i}^{2}}}\ .}$

Многокомпонентная диффузия и термодиффузия

Закон Фика описывает диффузию примеси в среде. Концентрация этой примеси должна быть мала, а градиент этой концентрации также должен быть мал. Движущей силой диффузии в законе Фика является антиградиент концентрации, . ${\displaystyle -\nabla n}$

В 1931 году Ларс Онзагер ^[13] включил многокомпонентные транспортные процессы в общий контекст линейной неравновесной термодинамики. Для многокомпонентного транспорта,

${\displaystyle \mathbf {J} _{i}=\sum _{j}L_{ij}X_{j}\,,}$

где - поток -й физической величины (компоненты), -й термодинамическая сила и - матрица Онзагера кинетических коэффициентов переноса . ${\displaystyle \mathbf {J} _{i}}$ ${\displaystyle i}$ ${\displaystyle X_{j}}$ ${\displaystyle j}$ ${\displaystyle L_{ij}}$

Термодинамические силы для процессов переноса были введены Онзагером как пространственные градиенты производных плотности энтропии (он использовал термин «сила» в кавычках или «движущая сила»): ${\displaystyle s}$

${\displaystyle X_{i}=\nabla {\frac {\partial s(n)}{\partial n_{i}}}\,,}$

где - "термодинамические координаты". Для переноса тепла и массы можно взять (плотность внутренней энергии), а - концентрация го компонента. Соответствующие движущие силы - пространственные векторы ${\displaystyle n_{i}}$ ${\displaystyle n_{0}=u}$ ${\displaystyle n_{i}}$ ${\displaystyle i}$

${\displaystyle X_{0}=\nabla {\frac {1}{T}}\ ,\;\;\;X_{i}=-\nabla {\frac {\mu _{i}}{T}}\;(i>0),}$потому что ${\displaystyle \mathrm {d} s={\frac {1}{T}}\,\mathrm {d} u-\sum _{i\geq 1}{\frac {\mu _{i}}{T}}\,{\rm {d}}n_{i}}$

где T — абсолютная температура, а — химический потенциал th-го компонента. Следует подчеркнуть, что отдельные уравнения диффузии описывают смешение или массоперенос без объемного движения. Поэтому члены с изменением общего давления пренебрегаются. Это возможно для диффузии малых примесей и для малых градиентов. ${\displaystyle \mu _{i}}$ ${\displaystyle i}$

Для линейных уравнений Онзагера мы должны взять термодинамические силы в линейном приближении вблизи равновесия:

${\displaystyle X_{i}=\sum _{k\geq 0}\left.{\frac {\partial ^{2}s(n)}{\partial n_{i}\,\partial n_{k}}}\right|_{n=n^{*}}\nabla n_{k}\ ,}$

где производные вычисляются в равновесии . Матрица кинетических коэффициентов должна быть симметричной ( взаимные соотношения Онзагера ) и положительно определенной ( для роста энтропии ). ${\displaystyle s}$ ${\displaystyle n^{*}}$ ${\displaystyle L_{ij}}$

Уравнения переноса следующие:

${\displaystyle {\frac {\partial n_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=-\sum _{j\geq 0}L_{ij}\operatorname {div} X_{j}=\sum _{k\geq 0}\left[-\sum _{j\geq 0}L_{ij}\left.{\frac {\partial ^{2}s(n)}{\partial n_{j}\,\partial n_{k}}}\right|_{n=n^{*}}\right]\,\Delta n_{k}\ .}$

Здесь все индексы i , j , k = 0, 1, 2, ... связаны с внутренней энергией (0) и различными компонентами. Выражение в квадратных скобках представляет собой матрицу коэффициентов диффузии ( i , k  > 0), термодиффузии ( i  > 0, k  = 0 или k  > 0, i  = 0) и теплопроводности ( i = k = 0 ). ${\displaystyle D_{ik}}$

При изотермических условиях T  = константа. Соответствующий термодинамический потенциал — это свободная энергия (или свободная энтропия ). Термодинамические движущие силы изотермической диффузии — это антиградиенты химических потенциалов, , а матрица коэффициентов диффузии — это ${\displaystyle -(1/T)\,\nabla \mu _{j}}$

${\displaystyle D_{ik}={\frac {1}{T}}\sum _{j\geq 1}L_{ij}\left.{\frac {\partial \mu _{j}(n,T)}{\partial n_{k}}}\right|_{n=n^{*}}}$

( я, к  > 0).

В определении термодинамических сил и кинетических коэффициентов присутствует внутренняя произвольность, поскольку они неизмеримы по отдельности, а измерять можно только их комбинации. Например, в оригинальной работе Онзагера ^[13] термодинамические силы включают дополнительный множитель T , тогда как в Курсе теоретической физики ^[14] этот множитель опущен, но знак термодинамических сил противоположен. Все эти изменения дополняются соответствующими изменениями коэффициентов и не влияют на измеряемые величины. ${\textstyle \sum _{j}L_{ij}X_{j}}$

Недиагональная диффузия должна быть нелинейной.

Формализм линейной необратимой термодинамики (Онзагер) порождает системы линейных уравнений диффузии в виде

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=\sum _{j}D_{ij}\,\Delta c_{j}.}$

Если матрица коэффициентов диффузии диагональна, то эта система уравнений представляет собой просто набор развязанных уравнений Фика для различных компонентов. Предположим, что диффузия недиагональна, например, , и рассмотрим состояние с . В этом состоянии . Если в некоторых точках, то становится отрицательным в этих точках за короткое время. Следовательно, линейная недиагональная диффузия не сохраняет положительность концентраций. Недиагональные уравнения многокомпонентной диффузии должны быть нелинейными. ^[12] ${\displaystyle D_{12}\neq 0}$ ${\displaystyle c_{2}=\cdots =c_{n}=0}$ ${\displaystyle \partial c_{2}/\partial t=D_{12}\,\Delta c_{1}}$ ${\displaystyle D_{12}\,\Delta c_{1}(x)<0}$ ${\displaystyle c_{2}(x)}$

Приложенные силы

Соотношение Эйнштейна (кинетическая теория) связывает коэффициент диффузии и подвижность (отношение конечной скорости дрейфа частицы к приложенной силе ). ^[15] Для заряженных частиц:

${\displaystyle D={\frac {\mu \,k_{\text{B}}T}{q}},}$

где D — константа диффузии , μ — «подвижность», k _B — постоянная Больцмана , T — абсолютная температура , а q — элементарный заряд , то есть заряд одного электрона.

Ниже, чтобы объединить в одной формуле химический потенциал μ и подвижность, мы используем для подвижности обозначение . ${\displaystyle {\mathfrak {m}}}$

Диффузия через мембрану

Подход, основанный на подвижности, был далее применен Т. Теорелем. ^[16] В 1935 году он исследовал диффузию ионов через мембрану. Суть своего подхода он сформулировал в формуле:

поток равен подвижности × концентрации × силе на грамм-ион .

Это так называемая формула Теорелла . ^{[ необходима цитата ]} Термин «грамм-ион» («грамм-частица») используется для количества вещества, которое содержит число Авогадро ионов (частиц). Общепринятый современный термин — моль .

Сила в изотермических условиях состоит из двух частей:

1. Сила диффузии, вызванная градиентом концентрации: . ${\displaystyle -RT{\frac {1}{n}}\,\nabla n=-RT\,\nabla (\ln(n/n^{\text{eq}}))}$
2. Электростатическая сила, вызванная градиентом электрического потенциала: . ${\displaystyle q\,\nabla \varphi }$

Здесь R — газовая постоянная, T — абсолютная температура, n — концентрация, равновесная концентрация отмечена верхним индексом «eq», q — заряд, φ — электрический потенциал.

Простым, но решающим отличием формулы Теорелла от законов Онзагера является фактор концентрации в выражении Теорелла для потока. В подходе Эйнштейна–Теорелла, если для конечной силы концентрация стремится к нулю, то поток также стремится к нулю, тогда как уравнения Онзагера нарушают это простое и физически очевидное правило.

Общая формулировка формулы Теорелла для неидеальных систем в изотермических условиях имеет вид ^[12]

${\displaystyle \mathbf {J} ={\mathfrak {m}}\exp \left({\frac {\mu -\mu _{0}}{RT}}\right)(-\nabla \mu +({\text{external force per mole}})),}$

где μ - химический потенциал , μ ₀ - стандартное значение химического потенциала. Выражение представляет собой так называемую активность . Она измеряет "эффективную концентрацию" вида в неидеальной смеси. В этой записи формула Теорелла для потока имеет очень простой вид ^[12] ${\displaystyle a=\exp \left({\frac {\mu -\mu _{0}}{RT}}\right)}$

${\displaystyle \mathbf {J} ={\mathfrak {m}}a(-\nabla \mu +({\text{external force per mole}})).}$

Стандартное выведение активности включает нормировочный фактор и для малых концентраций , где - стандартная концентрация. Поэтому эта формула для потока описывает поток нормализованной безразмерной величины : ${\displaystyle a=n/n^{\ominus }+o(n/n^{\ominus })}$ ${\displaystyle n^{\ominus }}$ ${\displaystyle n/n^{\ominus }}$

${\displaystyle {\frac {\partial (n/n^{\ominus })}{\partial t}}=\nabla \cdot [{\mathfrak {m}}a(\nabla \mu -({\text{external force per mole}}))].}$

Баллистическая шкала времени

Модель Эйнштейна игнорирует инерцию рассеивающейся части. Альтернативное уравнение Ланжевена начинается со второго закона движения Ньютона: ^[17]

${\displaystyle m{\frac {d^{2}x}{dt^{2}}}=-{\frac {1}{\mu }}{\frac {dx}{dt}}+F(t)}$

где

• x — позиция.
• μ — подвижность частицы в жидкости или газе, которую можно рассчитать с помощью соотношения Эйнштейна (кинетическая теория) .
• m — масса частицы.
• F — случайная сила, приложенная к частице.
• т - время.

Решая это уравнение, можно получить зависящую от времени константу диффузии в пределе больших времен и когда частица значительно плотнее окружающей жидкости, ^[17]

${\displaystyle D(t)=\mu \,k_{\rm {B}}T(1-e^{-t/(m\mu )})}$

где

• k _B — постоянная Больцмана ;
• T — абсолютная температура .
• μ — подвижность частицы в жидкости или газе, которую можно рассчитать с помощью соотношения Эйнштейна (кинетическая теория) .
• m — масса частицы.
• т - время.

В длинных временных масштабах результат Эйнштейна восстанавливается, но в коротких временных масштабах баллистический режим также объясняется. Более того, в отличие от подхода Эйнштейна, скорость может быть определена, что приводит к теореме о флуктуации-диссипации , связывающей конкуренцию между трением и случайными силами при определении температуры. ^{[17] : 3.2}

Прыжки на поверхности и в твердых телах

Диффузия в монослое: колебания вблизи временных положений равновесия и скачки в ближайшие свободные места.

Диффузия реагентов на поверхности катализатора может играть важную роль в гетерогенном катализе. Модель диффузии в идеальном монослое основана на прыжках реагентов на ближайшие свободные места. Эта модель была использована для окисления CO на Pt при низком давлении газа .

Система включает несколько реагентов на поверхности. Их поверхностные концентрации равны Поверхность представляет собой решетку мест адсорбции. Каждая молекула реагента заполняет место на поверхности. Часть мест свободна. Концентрация свободных мест равна . Сумма всех (включая свободные места) постоянна, плотность мест адсорбции b . ${\displaystyle A_{1},A_{2},\ldots ,A_{m}}$ ${\displaystyle c_{1},c_{2},\ldots ,c_{m}.}$ ${\displaystyle z=c_{0}}$ ${\displaystyle c_{i}}$

Модель скачка дает для диффузионного потока ( i  = 1, ...,  n ): ${\displaystyle A_{i}}$

${\displaystyle \mathbf {J} _{i}=-D_{i}[z\,\nabla c_{i}-c_{i}\nabla z]\,.}$

Соответствующее уравнение диффузии имеет вид: ^[12]

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=-\operatorname {div} \mathbf {J} _{i}=D_{i}[z\,\Delta c_{i}-c_{i}\,\Delta z]\,.}$

В силу закона сохранения, и имеем систему из m уравнений диффузии. Для одного компонента получаем закон Фика и линейные уравнения, так как . Для двух и более компонентов уравнения нелинейные. ${\displaystyle z=b-\sum _{i=1}^{n}c_{i}\,,}$ ${\displaystyle (b-c)\,\nabla c-c\,\nabla (b-c)=b\,\nabla c}$

Если все частицы могут меняться местами со своими ближайшими соседями, то простое обобщение дает

${\displaystyle \mathbf {J} _{i}=-\sum _{j}D_{ij}[c_{j}\,\nabla c_{i}-c_{i}\,\nabla c_{j}]}$

${\displaystyle {\frac {\partial c_{i}}{\partial t}}=\sum _{j}D_{ij}[c_{j}\,\Delta c_{i}-c_{i}\,\Delta c_{j}]}$

где - симметричная матрица коэффициентов, характеризующих интенсивности скачков. Свободные места (вакансии) следует рассматривать как особые «частицы» с концентрацией . ${\displaystyle D_{ij}=D_{ji}\geq 0}$ ${\displaystyle c_{0}}$

Различные версии этих моделей скачков подходят также для простых механизмов диффузии в твердых телах.

Пористая среда

Для диффузии в пористых средах основными уравнениями являются (если Φ постоянна): ^[18]

${\displaystyle \mathbf {J} =-\phi D\,\nabla n^{m}}$

${\displaystyle {\frac {\partial n}{\partial t}}=D\,\Delta n^{m}\,,}$

где D — коэффициент диффузии, Φ — пористость, n — концентрация, m  > 0 (обычно m  > 1, случай m  = 1 соответствует закону Фика).

Необходимо позаботиться о том, чтобы правильно учесть пористость (Φ) пористой среды как в терминах потока, так и в терминах накопления. ^[19] Например, когда пористость стремится к нулю, молярный поток в пористой среде стремится к нулю для заданного градиента концентрации. При применении дивергенции потока члены пористости сокращаются, и формируется второе уравнение выше.

Для диффузии газов в пористой среде это уравнение является формализацией закона Дарси : объемный поток газа в пористой среде равен

${\displaystyle q=-{\frac {k}{\mu }}\,\nabla p}$

где k — проницаемость среды, μ — вязкость , p — давление.

Адвективный молярный поток определяется как

J  =  nq

и для закона Дарси дает уравнение диффузии в пористой среде с m  =  γ  + 1. ${\displaystyle p\sim n^{\gamma }}$

В пористых средах средняя линейная скорость (ν) связана с объемным потоком следующим образом:

${\displaystyle \upsilon =q/\phi }$

Объединение адвективного молярного потока с диффузионным потоком дает уравнение адвективной дисперсии

${\displaystyle {\frac {\partial n}{\partial t}}=D\,\Delta n^{m}\ -\nu \cdot \nabla n^{m},}$

Для инфильтрации подземных вод приближение Буссинеска дает то же самое уравнение с  m  = 2.

Для плазмы с высоким уровнем излучения уравнение Зельдовича -Райзера дает m  > 4 для теплопередачи.

Диффузия в физике

Коэффициент диффузии в кинетической теории газов

Случайные столкновения частиц в газе.

Коэффициент диффузии — это коэффициент в первом законе Фика , где J — диффузионный поток ( количество вещества ) на единицу площади за единицу времени, n (для идеальных смесей) — концентрация, x — положение [длина]. ${\displaystyle D}$ ${\displaystyle J=-D\,\partial n/\partial x}$

Рассмотрим два газа с молекулами одинакового диаметра d и массы m ( самодиффузия ). В этом случае элементарная теория свободного пробега диффузии дает для коэффициента диффузии

${\displaystyle D={\frac {1}{3}}\ell v_{T}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}m}}}{\frac {T^{3/2}}{Pd^{2}}}\,,}$

где k _B — постоянная Больцмана , T — температура , P — давление , — средняя длина свободного пробега , а v _T — средняя тепловая скорость: ${\displaystyle \ell }$

${\displaystyle \ell ={\frac {k_{\rm {B}}T}{{\sqrt {2}}\pi d^{2}P}}\,,\;\;\;v_{T}={\sqrt {\frac {8k_{\rm {B}}T}{\pi m}}}\,.}$

Мы видим, что коэффициент диффузии в приближении средней длины свободного пробега растет с ростом T как T ^3/2 и уменьшается с ростом P как 1/ P. Если мы используем для P закон идеального газа P  =  RnT с полной концентрацией n , то мы видим, что для данной концентрации n коэффициент диффузии растет с ростом T как T ^1/2 , а для данной температуры он уменьшается с полной концентрацией как 1/ n .

Для двух различных газов, A и B, с молекулярными массами m _A , m _B и молекулярными диаметрами d _A , d _B оценка средней длины свободного пробега коэффициента диффузии A в B и B в A равна:

${\displaystyle D_{\rm {AB}}={\frac {2}{3}}{\sqrt {\frac {k_{\rm {B}}^{3}}{\pi ^{3}}}}{\sqrt {{\frac {1}{2m_{\rm {A}}}}+{\frac {1}{2m_{\rm {B}}}}}}{\frac {4T^{3/2}}{P(d_{\rm {A}}+d_{\rm {B}})^{2}}}\,,}$

Теория диффузии в газах, основанная на уравнении Больцмана

В кинетике Больцмана смеси газов каждый газ имеет свою собственную функцию распределения, , где t - момент времени, x - положение, а c - скорость молекулы i -го компонента смеси. Каждый компонент имеет свою среднюю скорость . Если скорости не совпадают, то имеет место диффузия . ${\displaystyle f_{i}(x,c,t)}$ ${\textstyle C_{i}(x,t)={\frac {1}{n_{i}}}\int _{c}cf(x,c,t)\,dc}$ ${\displaystyle C_{i}(x,t)}$

В приближении Чепмена–Энскога все функции распределения выражаются через плотности сохраняющихся величин: ^[10]

• индивидуальные концентрации частиц (частиц на объем), ${\textstyle n_{i}(x,t)=\int _{c}f_{i}(x,c,t)\,dc}$
• плотность импульса ( m _i — масса i- й частицы), ${\textstyle \sum _{i}m_{i}n_{i}C_{i}(x,t)}$
• плотность кинетической энергии $${\displaystyle \sum _{i}\left(n_{i}{\frac {m_{i}C_{i}^{2}(x,t)}{2}}+\int _{c}{\frac {m_{i}(c_{i}-C_{i}(x,t))^{2}}{2}}f_{i}(x,c,t)\,dc\right).}$$

Кинетическая температура T и давление P определяются в трехмерном пространстве как

${\displaystyle {\frac {3}{2}}k_{\rm {B}}T={\frac {1}{n}}\int _{c}{\frac {m_{i}(c_{i}-C_{i}(x,t))^{2}}{2}}f_{i}(x,c,t)\,dc;\quad P=k_{\rm {B}}nT,}$

где - общая плотность. ${\textstyle n=\sum _{i}n_{i}}$

Для двух газов разность скоростей определяется выражением: ^[10] ${\displaystyle C_{1}-C_{2}}$

${\displaystyle C_{1}-C_{2}=-{\frac {n^{2}}{n_{1}n_{2}}}D_{12}\left\{\nabla \left({\frac {n_{1}}{n}}\right)+{\frac {n_{1}n_{2}(m_{2}-m_{1})}{Pn(m_{1}n_{1}+m_{2}n_{2})}}\nabla P-{\frac {m_{1}n_{1}m_{2}n_{2}}{P(m_{1}n_{1}+m_{2}n_{2})}}(F_{1}-F_{2})+k_{T}{\frac {1}{T}}\nabla T\right\},}$

где — сила, приложенная к молекулам i -го компонента, — коэффициент термодиффузии. ${\displaystyle F_{i}}$ ${\displaystyle k_{T}}$

Коэффициент D ₁₂ положителен. Это коэффициент диффузии. Четыре члена в формуле для C ₁ − C ₂ описывают четыре основных эффекта диффузии газов:

1. ${\displaystyle \nabla \,\left({\frac {n_{1}}{n}}\right)}$описывает поток первой компоненты из областей с большим отношением n ₁ / n в области с меньшими значениями этого отношения (и, аналогично, поток второй компоненты из больших n ₂ / n в меньшие n ₂ / n , поскольку n ₂ / n  = 1 –  n ₁ / n );
2. ${\displaystyle {\frac {n_{1}n_{2}(m_{2}-m_{1})}{n(m_{1}n_{1}+m_{2}n_{2})}}\nabla P}$описывает поток более тяжелых молекул в области с более высоким давлением, а более легких молекул в области с более низким давлением, это бародиффузия;
3. ${\displaystyle {\frac {m_{1}n_{1}m_{2}n_{2}}{P(m_{1}n_{1}+m_{2}n_{2})}}(F_{1}-F_{2})}$описывает диффузию, вызванную разницей сил, приложенных к молекулам разных типов. Например, в гравитационном поле Земли более тяжелые молекулы должны опускаться вниз, или в электрическом поле заряженные молекулы должны двигаться, пока этот эффект не будет уравновешен суммой других членов. Этот эффект не следует путать с бародиффузией, вызванной градиентом давления.
4. ${\displaystyle k_{T}{\frac {1}{T}}\nabla T}$описывает термодиффузию — диффузионный поток, вызванный градиентом температуры.

Все эти эффекты называются диффузией , поскольку они описывают различия в скоростях различных компонентов в смеси. Поэтому эти эффекты не могут быть описаны как массовый перенос и отличаются от адвекции или конвекции.

В первом приближении ^[10]

• $${\displaystyle D_{12}={\frac {3}{2n(d_{1}+d_{2})^{2}}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}}$$для жестких сфер;
• $${\displaystyle D_{12}={\frac {3}{8nA_{1}({\nu })\Gamma (3-{\frac {2}{\nu -1}})}}\left[{\frac {kT(m_{1}+m_{2})}{2\pi m_{1}m_{2}}}\right]^{1/2}\left({\frac {2kT}{\kappa _{12}}}\right)^{\frac {2}{\nu -1}}}$$для отталкивающей силы ${\displaystyle \kappa _{12}r^{-\nu }.}$

Число определяется квадратурами (формулы (3.7), (3.9), гл. 10 классической книги Чепмена и Коулинга ^[10] ) ${\displaystyle A_{1}({\nu })}$

Мы видим, что зависимость от T для жестких сфер та же, что и для простой теории среднего свободного пробега, но для законов силового отталкивания показатель степени другой. Зависимость от полной концентрации n для данной температуры всегда имеет тот же характер, 1/ n .

В приложениях к газовой динамике диффузионный поток и объемный поток должны быть объединены в одну систему уравнений переноса. Объемный поток описывает перенос массы. Его скорость V является средней скоростью массы. Она определяется через плотность импульса и концентрации массы:

${\displaystyle V={\frac {\sum _{i}\rho _{i}C_{i}}{\rho }}\,.}$

где - массовая концентрация i- го вида, - массовая плотность. ${\displaystyle \rho _{i}=m_{i}n_{i}}$ ${\textstyle \rho =\sum _{i}\rho _{i}}$

По определению скорость диффузии i- го компонента равна , . Массоперенос i- го компонента описывается уравнением неразрывности ${\displaystyle v_{i}=C_{i}-V}$ ${\textstyle \sum _{i}\rho _{i}v_{i}=0}$

${\displaystyle {\frac {\partial \rho _{i}}{\partial t}}+\nabla (\rho _{i}V)+\nabla (\rho _{i}v_{i})=W_{i}\,,}$

где - чистая скорость производства массы в химических реакциях, . ${\displaystyle W_{i}}$ ${\textstyle \sum _{i}W_{i}=0}$

В этих уравнениях член описывает адвекцию i -го компонента, а член представляет диффузию этого компонента. ${\displaystyle \nabla (\rho _{i}V)}$ ${\displaystyle \nabla (\rho _{i}v_{i})}$

В 1948 году Уэнделл Х. Фурри предложил использовать форму скоростей диффузии, найденную в кинетической теории, в качестве основы для нового феноменологического подхода к диффузии в газах. Этот подход был далее развит FA Williams и SH Lam. ^[20] Для скоростей диффузии в многокомпонентных газах ( N компонентов) они использовали

${\displaystyle v_{i}=-\left(\sum _{j=1}^{N}D_{ij}\mathbf {d} _{j}+D_{i}^{(T)}\,\nabla (\ln T)\right)\,;}$

${\displaystyle \mathbf {d} _{j}=\nabla X_{j}+(X_{j}-Y_{j})\,\nabla (\ln P)+\mathbf {g} _{j}\,;}$

${\displaystyle \mathbf {g} _{j}={\frac {\rho }{P}}\left(Y_{j}\sum _{k=1}^{N}Y_{k}(f_{k}-f_{j})\right)\,.}$

Здесь — матрица коэффициентов диффузии, — коэффициент термодиффузии, — объемная сила на единицу массы, действующая на i -й вид, — доля парциального давления i - го вида (и — парциальное давление), — массовая доля i -го вида, и ${\displaystyle D_{ij}}$ ${\displaystyle D_{i}^{(T)}}$ ${\displaystyle f_{i}}$ ${\displaystyle X_{i}=P_{i}/P}$ ${\displaystyle P_{i}}$ ${\displaystyle Y_{i}=\rho _{i}/\rho }$ ${\textstyle \sum _{i}X_{i}=\sum _{i}Y_{i}=1.}$

Поскольку носители генерируются (зеленые: электроны и фиолетовые: дырки) из-за света, падающего на центр собственного полупроводника, они диффундируют к двум концам. Электроны имеют более высокую константу диффузии, чем дырки, что приводит к меньшему количеству избыточных электронов в центре по сравнению с дырками.

Диффузия электронов в твердых телах

Когда плотность электронов в твердых телах не находится в равновесии, происходит диффузия электронов. Например, когда смещение приложено к двум концам куска полупроводника, или свет падает на один конец (см. правый рисунок), электроны диффундируют из областей с высокой плотностью (в центре) в области с низкой плотностью (два конца), образуя градиент электронной плотности. Этот процесс генерирует ток, называемый диффузионным током .

Диффузионный ток также можно описать первым законом Фика.

${\displaystyle J=-D\,\partial n/\partial x\,,}$

где J — плотность диффузионного тока ( количество вещества ) на единицу площади в единицу времени, n (для идеальных смесей) — электронная плотность, x — положение [длина].

Диффузия в геофизике

Аналитические и численные модели, решающие уравнение диффузии для различных начальных и граничных условий, были популярны для изучения широкого спектра изменений на поверхности Земли. Диффузия широко использовалась в исследованиях эрозии отступления склона холма, эрозии обрыва, деградации уступа сброса, отступления террасы/береговой линии волнореза, врезания аллювиального канала, отступления прибрежного шельфа и выдвижения дельты. ^[21] Хотя поверхность Земли не является буквально диффузной во многих из этих случаев, процесс диффузии эффективно имитирует целостные изменения, которые происходят на протяжении десятилетий или тысячелетий. Модели диффузии также могут использоваться для решения обратных граничных задач, в которых некоторая информация об осадочной среде известна из палеоэкологической реконструкции, а уравнение диффузии используется для вычисления притока осадков и временных рядов изменений рельефа. ^[22]

Диализ

Схема полупроницаемой мембраны во время гемодиализа , где кровь красная, диализирующая жидкость синяя, а мембрана желтая.

Диализ работает по принципу диффузии растворенных веществ и ультрафильтрации жидкости через полупроницаемую мембрану . Диффузия является свойством веществ в воде; вещества в воде имеют тенденцию перемещаться из области высокой концентрации в область низкой концентрации. ^[23] Кровь течет по одной стороне полупроницаемой мембраны, а диализат, или специальная диализная жидкость, течет по противоположной стороне. Полупроницаемая мембрана представляет собой тонкий слой материала, который содержит отверстия различных размеров, или поры. Более мелкие растворенные вещества и жидкость проходят через мембрану, но мембрана блокирует прохождение более крупных веществ (например, эритроцитов и крупных белков). Это повторяет процесс фильтрации, который происходит в почках, когда кровь поступает в почки, и более крупные вещества отделяются от более мелких в клубочках . ^[23]

Случайное блуждание (случайное движение)

Объяснено кажущееся случайное движение атомов, ионов или молекул. Вещества кажутся движущимися случайным образом из-за столкновений с другими веществами. Из книги iBook Cell Membrane Transport , бесплатная лицензия предоставлена ​​IS3D, LLC, 2014.

Одно из распространенных заблуждений заключается в том, что отдельные атомы, ионы или молекулы движутся хаотично, что на самом деле не так. На анимации справа ион на левой панели, по-видимому, движется «хаотично» в отсутствие других ионов. Однако, как показывает правая панель, это движение не случайно, а является результатом «столкновений» с другими ионами. Таким образом, движение одного атома, иона или молекулы в смеси кажется случайным, если рассматривать его изолированно. Движение вещества в смеси путем «случайного блуждания» регулируется кинетической энергией внутри системы, на которую могут влиять изменения концентрации, давления или температуры. (Это классическое описание. В меньших масштабах квантовые эффекты, как правило, не будут пренебрежимо малыми. Таким образом, изучение движения одного атома становится более тонким, поскольку частицы в таких малых масштабах описываются амплитудами вероятности, а не детерминированными мерами положения и скорости.)

Разделение диффузии и конвекции в газах

В то время как броуновское движение многомолекулярных мезоскопических частиц (вроде зерен пыльцы, изученных Брауном) можно наблюдать под оптическим микроскопом, молекулярную диффузию можно исследовать только в тщательно контролируемых экспериментальных условиях. Со времен экспериментов Грэхема хорошо известно, что необходимо избегать конвекции, и это может быть нетривиальной задачей.

При нормальных условиях молекулярная диффузия доминирует только на длинах в диапазоне от нанометра до миллиметра. На больших масштабах длины транспорт в жидкостях и газах обычно обусловлен другим явлением транспорта — конвекцией . Для разделения диффузии в этих случаях требуются особые усилия.

Напротив, теплопроводность через твердые среды является повседневным явлением (например, металлическая ложка, частично погруженная в горячую жидкость). Это объясняет, почему диффузия тепла была объяснена математически до диффузии массы.

Другие типы диффузии

• Анизотропная диффузия , также известная как уравнение Пероны-Малика, усиливает высокие градиенты
• Атомная диффузия в твердых телах
• Бома диффузия , распространение плазмы через магнитные поля
• Вихревая диффузия в грубом описании турбулентного течения
• Истечение газа через небольшие отверстия
• Электронная диффузия, приводящая к возникновению электрического тока, называемого диффузионным током.
• Облегченная диффузия , присутствующая в некоторых организмах
• Газовая диффузия , используемая для разделения изотопов
• Уравнение теплопроводности , диффузия тепловой энергии
• Ито-диффузия , математизация броуновского движения, непрерывный случайный процесс.
• Кнудсеновская диффузия газа в длинных порах с частыми столкновениями со стенками
• Полет Леви
• Молекулярная диффузия , диффузия молекул из более плотных областей в менее плотные.
• Диффузия импульса , например диффузия гидродинамического поля скорости
• Рассеивание фотонов
• Плазменная диффузия
• Случайное блуждание , ^[24] модель диффузии
• Обратная диффузия , против градиента концентрации, при разделении фаз
• Вращательная диффузия , случайная переориентация молекул
• Спиновая диффузия , диффузия спиновых магнитных моментов в твердых телах
• Поверхностная диффузия , диффузия адчастиц на поверхности
• Такси — это направленная двигательная активность животного в ответ на раздражитель.
  • Кинезис — это ненаправленная двигательная активность животного в ответ на раздражитель.
• Транскультурная диффузия , распространение культурных черт по географическому региону
• Турбулентная диффузия , перенос массы, тепла или импульса в турбулентной жидкости.

Смотрите также

• Аномальная диффузия  – процесс диффузии с нелинейной зависимостью от времени.
• Уравнение конвекции-диффузии  – комбинация уравнений диффузии и конвекции (адвекции)
• Агрегация, ограниченная диффузией
• Уравнения Даркена
• Изобарическая контрдиффузия  – диффузия газа через ткани тела при постоянном общем давлении.
• Сорбция  – физический или химический процесс, посредством которого одно вещество присоединяется к другому.
• Осмос  – миграция молекул в область с более низкой концентрацией растворенного вещества.
• Теория перколяции  – Математическая теория поведения связанных кластеров в случайном графе.
• Социальные сети  – журналPages displaying wikidata descriptions as a fallbackPages displaying short descriptions with no spaces

Ссылки

1. JG Kirkwood , RL Baldwin, PJ Dunlop, LJ Gosting, G. Kegeles (1960) Уравнения потока и системы отсчета для изотермической диффузии в жидкостях. Журнал химической физики 33(5):1505–13.
2. Muir, DCF (1966-10-01). «Объемный поток и диффузия в дыхательных путях легких». British Journal of Diseases of the Chest . 60 (4): 169–176. doi :10.1016/S0007-0971(66)80044-X. ISSN  0007-0971. PMID  5969933.
3. J. Philibert (2005). Полтора столетия диффузии: Фик, Эйнштейн, до и после. Архивировано 13 декабря 2013 г. в Wayback Machine Diffusion Fundamentals, 2, 1.1–1.10.
4. SR Де Гроот, П. Мазур (1962). Неравновесная термодинамика . Северная Голландия, Амстердам.
5. А. Эйнштейн (1905). «Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flussigkeiten suspendierten Teilchen». Энн. Физ . 17 (8): 549–60. Бибкод : 1905АнП...322..549Е. дои : 10.1002/andp.19053220806 .
6. Пескармона, ПП (2020). Гитис, В.; Ротенберг, Г. (ред.). Справочник по пористым материалам. Том 4. Сингапур: WORLD SCIENTIFIC. стр. 150–151. doi :10.1142/11909. ISBN 978-981-12-2328-0.
7. Диффузионные процессы , Симпозиум Томаса Грэма, ред. Дж. Н. Шервуда, А. В. Чедвика, В. М. Мьюира, Ф. Л. Суинтона, Гордона и Брича, Лондон, 1971.
8. Л.В. Барр (1997), В: Распространение материалов, DIMAT 96 , изд. Х.Мерер, Хр. Герциг, Н. А. Столвейк, Х. Брахт, Scitec Publications, Том 1, стр. 1–9.
9. Х. Мерер; Н. А. Столвейк (2009). «Герои и яркие моменты в истории распространения» (PDF) . Основы диффузии . 11 (1): 1–32.
10. S. Chapman, TG Cowling (1970) Математическая теория неоднородных газов: изложение кинетической теории вязкости, теплопроводности и диффузии в газах , Cambridge University Press (3-е издание), ISBN 052140844X . 
11. JF Kincaid; H. Eyring; AE Stearn (1941). «Теория абсолютных скоростей реакции и ее применение к вязкости и диффузии в жидком состоянии». Chem. Rev. 28 ( 2): 301–65. doi :10.1021/cr60090a005.
12. AN Gorban , HP Sargsyan и HA Wahab (2011). "Квазихимические модели многокомпонентной нелинейной диффузии". Математическое моделирование природных явлений . 6 (5): 184–262. arXiv : 1012.2908 . doi : 10.1051/mmnp/20116509 . S2CID  18961678.
13. Онзагер, Л. (1931). «Взаимные отношения в необратимых процессах. I». Physical Review . 37 (4): 405–26. Bibcode :1931PhRv...37..405O. doi : 10.1103/PhysRev.37.405 .
14. Л. Д. Ландау , Е. М. Лифшиц (1980). Статистическая физика . Т. 5 (3-е изд.). Баттерворт-Хайнеман . ISBN 978-0-7506-3372-7.
15. S. Bromberg, KA Dill (2002), Молекулярные движущие силы: статистическая термодинамика в химии и биологии, Garland Science, ISBN 0815320515 . 
16. T. Teorell (1935). «Исследования «эффекта диффузии» при ионном распределении. Некоторые теоретические соображения». Труды Национальной академии наук Соединенных Штатов Америки . 21 (3): 152–61. Bibcode :1935PNAS...21..152T. doi : 10.1073/pnas.21.3.152 . PMC 1076553 . PMID  16587950. 
17. Bian, Xin; Kim, Changho; Karniadakis, George Em (2016-08-14). "111 лет броуновского движения". Soft Matter . 12 ( 30): 6331–6346. Bibcode : 2016SMat...12.6331B. doi : 10.1039/c6sm01153e. PMC 5476231. PMID  27396746. 
18. JL Vázquez (2006), Уравнение пористой среды. Математическая теория, Oxford Univ. Press, ISBN 0198569033 . 
19. Stauffer, Philip H.; Vrugt, Jasper A.; Turin, H. Jake; Gable, Carl W.; Soll, Wendy E. (2009). «Распутывание диффузии из адвекции в ненасыщенных пористых средах: экспериментальные данные, моделирование и неопределенность параметров». Vadose Zone Journal . 8 (2): 510. Bibcode : 2009VZJ.....8..510S. doi : 10.2136/vzj2008.0055. ISSN  1539-1663. S2CID  46200956.
20. SH Lam (2006). "Многокомпонентная диффузия снова" (PDF) . Физика жидкостей . 18 (7): 073101–073101–8. Bibcode : 2006PhFl...18g3101L. doi : 10.1063/1.2221312.
21. Пастернак, Грегори Б.; Браш, Грейс С.; Хилгартнер, Уильям Б. (2001-04-01). «Влияние исторических изменений в землепользовании на доставку осадков в субэстуарную дельту залива Чесапик». Процессы на поверхности Земли и формы рельефа . 26 (4): 409–27. Bibcode : 2001ESPL...26..409P. doi : 10.1002/esp.189. ISSN  1096-9837. S2CID  129080402.
22. Грегори Б. Пастернак. «Гидравлология, геоморфология и экогидравлика водоразделов :: Моделирование TFD». pasternack.ucdavis.edu . Получено 12 июня 2017 г.
23. Словарь медицины, сестринского дела и профессий здравоохранения Мосби . 7-е изд. Сент-Луис, Миссури; Мосби: 2006
24. Вайс, Г. (1994). Аспекты и приложения случайного блуждания . Северная Голландия. ISBN 978-0444816061.