Точка Ферма

В евклидовой геометрии точка Ферма треугольника , также называемая точкой Торричелли или точкой Ферма –Торричелли , — это точка, такая, что сумма трех расстояний от каждой из трех вершин треугольника до этой точки является наименьшей возможной ^[1] или, что то же самое, геометрической медианой трех вершин. Она так названа, потому что эта проблема была впервые поднята Ферма в частном письме Эванджелисте Торричелли , который ее решил.

Точка Ферма дает решение задач геометрической медианы и дерева Штейнера для трех точек.

Строительство

Точка Ферма треугольника с наибольшим углом, не превышающим 120°, — это просто его первый изогонический центр или X(13) ^[2] , который строится следующим образом:

Постройте равносторонний треугольник на каждой из двух произвольно выбранных сторон данного треугольника.
Проведите линию от каждой новой вершины к противоположной вершине исходного треугольника.
Две прямые пересекаются в точке Ферма.

Альтернативный метод следующий:

На каждой из двух произвольно выбранных сторон постройте равнобедренный треугольник с основанием на рассматриваемой стороне, углами в 30 градусов при основании и третьей вершиной каждого равнобедренного треугольника, лежащей вне исходного треугольника.
Для каждого равнобедренного треугольника нарисуйте окружность, в каждом случае с центром в новой вершине равнобедренного треугольника и с радиусом, равным каждой из двух новых сторон этого равнобедренного треугольника.
Пересечение внутри исходного треугольника между двумя окружностями является точкой Ферма.

Если угол треугольника больше 120°, точка Ферма находится в вершине тупого угла.

В дальнейшем «Случай 1» означает, что треугольник имеет угол, превышающий 120°. «Случай 2» означает, что ни один из углов треугольника не превышает 120°.

Расположение X(13)

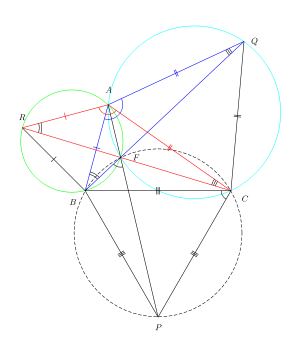
На рис. 2 показаны равносторонние треугольники $△ ARB, △ AQC, △ CPB ,$ присоединенные к сторонам произвольного треугольника $△ ABC$ . Вот доказательство, использующее свойства точек, лежащих на одной окружности, чтобы показать, что три линии $RC, BQ, AP$ на рис. 2 пересекаются в точке $F$ и пересекают друг друга под углами 60°.

Треугольники $△ RAC, △ BAQ$ равны , поскольку второй является поворотом первого на 60° вокруг $A$ . Следовательно, $∠$ $ARF$ $= ∠$ $ABF$ и $∠$ $AQF$ $= ∠$ $ACF$ . По обратной теореме о вписанном угле, $примененной$ к отрезку $AF$ , точки $ARBF$ являются конокружными (они лежат на одной окружности). Аналогично, точки AFCQ являются конокружными.

$∠ ARB = 60°$ , поэтому $∠ AFB = 120°$ , используя теорему о вписанном угле . Аналогично, $∠ AFC = 120°$ .

Итак , $∠ BFC = 120°$ . Следовательно, $∠ BFC + ∠ BPC = 180°$ . Используя теорему о вписанном угле , это означает, что точки $BPCF$ лежат на одной окружности. Итак, используя теорему о вписанном угле, примененную к отрезку $BP$ , $∠ BFP = ∠ BCP = 60°$ . Поскольку $∠ BFP + ∠ BFA = 180°$ , точка $F$ лежит на отрезке $AP$ . Итак, прямые $RC, BQ, AP$ пересекаются в одной точке. ЧТЭД

Это доказательство применимо только в случае 2, так как если $∠ BAC > 120°$ , точка $A$ лежит внутри описанной окружности $△ BPC,$ что меняет относительные положения $A$ и $F.$ Однако его легко модифицировать для случая 1. Тогда $∠ AFB = ∠ AFC = 60°,$ следовательно, $∠ BFC = ∠ AFB + ∠ AFC = 120°$ , что означает, что $BPCF$ является конциклической, поэтому $∠ BFP = ∠ BCP = 60° = ∠ BFA$ . Следовательно, $A$ лежит на $FP$ .

Прямые, соединяющие центры окружностей на рис. 2, перпендикулярны отрезкам $AP, BQ, CR$ . Например, прямая, соединяющая центр окружности, содержащей $△ ARB$ , и центр окружности, содержащей $△ AQC$ , перпендикулярна отрезку $AP$ . Таким образом, прямые, соединяющие центры окружностей, также пересекаются под углом 60°. Следовательно, центры окружностей образуют равносторонний треугольник. Это известно как теорема Наполеона .

Расположение точки Ферма

Традиционная геометрия

Дан любой евклидов треугольник $△ ABC$ и произвольная точка $P$ пусть Целью этого раздела является определение точки $P$ $0$ такой, что для всех Если такая точка существует, то она будет точкой Ферма. В дальнейшем $Δ$ будет обозначать точки внутри треугольника и будет считаться включающей его границу $Ω$ . $d(P)=|PA|+|PB|+|PC|.$ $d(P_{0})<d(P)$ $P\neq P_{0}.$

Ключевым результатом, который будет использован, является правило «собачьей ноги», которое утверждает, что если треугольник и многоугольник имеют одну общую сторону, а остальная часть треугольника лежит внутри многоугольника, то треугольник имеет меньший периметр, чем многоугольник:

Если

AB

— общая сторона, продлим

AC,

чтобы пересечь многоугольник в точке

X.

Тогда периметр многоугольника равен, по неравенству треугольника :

{\text{периметр}}>|AB|+|AX|+|XB|=|AB|+|AC|+|CX|+|XB|\geq |AB|+|AC|+|BC|.

Пусть $P$ будет любой точкой вне $Δ$ . Свяжите каждую вершину с ее удаленной зоной; то есть полуплоскостью за (расширенной) противоположной стороной. Эти 3 зоны покрывают всю плоскость, за исключением самой $Δ$ , и $P$ явно лежит либо в одной, либо в двух из них. Если $P$ находится в двух (скажем, пересечение зон $B$ и $C$ ), то установка подразумевает по правилу изгиба дуги. Альтернативно, если $P$ находится только в одной зоне, скажем, в зоне $A$ , то где $P'$ - пересечение $AP$ и $BC$ . Таким образом, для каждой точки $P$ вне $Δ$ существует точка $P'$ в $Ω$ такая, что $P'=A$ $d(P')=d(A)<d(P)$ $d(P')<d(P)$ $d(P')<d(P).$

Случай 1. Треугольник имеет угол ≥ 120°.

Без потери общности предположим, что угол при $A$ ≥ 120°. Постройте равносторонний треугольник $△ AFB$ и для любой точки $P$ в $Δ$ (кроме самой $A$ ) постройте $Q$ так, чтобы треугольник $△ AQP$ был равносторонним и имел указанную ориентацию. Тогда треугольник $△ ABP$ является поворотом на 60° треугольника $△ AFQ$ вокруг $A$ , так что эти два треугольника конгруэнтны, и отсюда следует, что это просто длина пути $CPQF$ . Поскольку $P$ ограничено лежать внутри $△$ $ABC$ , по правилу изгиба дуги длина этого пути превышает Поэтому для всех Теперь позвольте $P$ находиться вне $Δ$ . Из вышесказанного следует, что существует точка , такая что и как следует, что для всех $P$ вне $Δ$ . Таким образом, для всех , что означает, что $A$ является точкой Ферма для $Δ$ . Другими словами, точка Ферма лежит в тупоугольной вершине . $d(P)=|CP|+|PQ|+|QF|$ $|AC|+|AF|=d(A).$ $d(A)<d(P)$ $P\in \Delta ,P\neq A.$ $P'\in \Omega$ $d(P')<d(P)$ $d(A)\leq d(P')$ $d(A)<d(P)$ $d(A)<d(P)$ $P\neq A$

Случай 2. Треугольник не имеет углов ≥ 120°.

Постройте равносторонний треугольник $△ BCD$ , пусть $P$ — любая точка внутри $Δ$ , и постройте равносторонний треугольник $△ CPQ$ . Тогда $△ CQD$ — это поворот на 60° $△ CPB$ вокруг $C,$ поэтому

d(P)=|PA|+|PB|+|PC|=|AP|+|PQ|+|QD|

что является просто длиной пути $APQD$ . Пусть $P 0$ будет точкой пересечения $AD$ и $CF.$ Эту точку обычно называют первым изогоническим центром. Проделайте то же упражнение с $P 0$ , что и с $P$ , и найдите точку $Q 0$ . По угловому ограничению $P 0$ лежит внутри $△ ABC$ . Более того, $△ BCF$ является поворотом $△ BDA$ на 60° вокруг $B$ , поэтому $Q 0$ должна лежать где-то на $AD$ . Поскольку $∠ CDB = 60°,$ то $Q 0$ лежит между $P 0$ и $D$ , что означает $AP 0 Q 0 D$ является прямой линией, поэтому Более того, если то либо $P$ , либо $Q$ не будут лежать на $AD$ , что означает Теперь позвольте $P$ находиться вне $Δ$ . Из вышеизложенного следует, что существует точка , такая что и как следует, что для всех $P$ вне $Δ$ . Это означает, что $P$ $0$ является точкой Ферма для $Δ$ . Другими словами, точка Ферма совпадает с первым изогоническим центром . $d(P_{0}=|AD|.$ $P\neq P_{0}$ $d(P_{0})=|AD|<d(P).$ $P'\in \Omega$ $d(P')<d(P)$ $d(P_{0})\leq d(P')$ $d(P_{0})<d(P)$

Векторный анализ

Пусть $O, A, B, C, X$ — любые пять точек на плоскости. Обозначим векторы через $a$ $,$ $b$ $,$ $c$ $,$ $x$ соответственно, и пусть $i$ $,$ $j$ $,$ $k$ — единичные векторы из $O$ вдоль $a$ $,$ $b$ $,$ $c$ . ${\overrightarrow {OA}},\ {\overrightarrow {OB}},\ {\overrightarrow {OC}},\ {\overrightarrow {OX}}$

{\begin{aligned}|\mathbf {a} |&=\mathbf {a\cdot i} =(\mathbf {a} -\mathbf {x})\mathbf {\,\cdot \,i } +\mathbf {x\cdot i} \leq |\mathbf {a} -\mathbf {x} |+\mathbf {x\cdot i} ,\\|\mathbf {b} |&=\mathbf {b\cdot j} =(\mathbf {b} -\mathbf {x} )\mathbf {\,\ cdot \,j} +\mathbf {x\cdot j} \leq |\mathbf {b} -\mathbf {x} |+\mathbf {x\cdot j} ,\\|\mathbf {c} |&=\mathbf {c\cdot k} =(\mathbf {c} -\mathbf {x} )\mathbf {\,\cdot \,k} +\mathbf {x\cdot k} \leq |\mathbf {c} -\ mathbf {x} |+\mathbf {x\cdot k} .\end{aligned}}

Добавление $a, b, c$ дает

|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |\leq |\mathbf {a} -\mathbf {x} |+|\mathbf {b} -\mathbf {x} |+|\mathbf {c} -\mathbf {x} |+\mathbf {x} \cdot (\mathbf {i} +\mathbf {j} +\mathbf {k} ).

Если $a, b, c$ пересекаются в точке $O$ под углом 120°, то $i + j + k = 0$ , поэтому

|\mathbf {a} |+|\mathbf {b} |+|\mathbf {c} |\leq |\mathbf {a} -\mathbf {x} |+|\mathbf {b} -\mathbf {x} |+|\mathbf {c} -\mathbf {x} |

для всех $x$ . Другими словами,

|OA|+|OB|+|OC|\leq |XA|+|XB|+|XC|

и, следовательно, $O$ является точкой Ферма $△ ABC$ .

Этот аргумент не работает, когда треугольник имеет угол $∠ C > 120°$ , поскольку нет точки $O$ , где $a, b, c$ пересекаются под углом 120°. Тем не менее, это легко исправить, переопределив $k = - (i + j)$ и поместив $O$ в $C$ так, чтобы $c = 0$ . Обратите внимание, что $| k | \leq 1$ , поскольку угол между единичными векторами $i, j$ равен $∠ C$ , что превышает 120°. Поскольку

|\mathbf {0} |\leq |\mathbf {0} -\mathbf {x} |+\mathbf {x\cdot k} ,

третье неравенство все еще остается в силе, остальные два неравенства не изменяются. Доказательство теперь продолжается, как указано выше (складывая три неравенства и используя $i + j + k = 0$ ), чтобы прийти к тому же выводу, что $O$ (или в этом случае $C$ ) должна быть точкой Ферма $△ ABC$ .

Множители Лагранжа

Другой подход к нахождению точки внутри треугольника, от которой сумма расстояний до вершин треугольника минимальна, заключается в использовании одного из методов математической оптимизации , а именно метода множителей Лагранжа и теоремы косинусов .

Проведем линии из точки внутри треугольника к его вершинам и назовем их $X, Y, Z.$ Также пусть длины этих линий будут $x, y, z$ соответственно. Пусть угол между $X$ и $Y$ будет $α$ , $Y$ и $Z$ будет $β$ . Тогда угол между $X$ и $Z$ будет $π - α - β$ . Используя метод множителей Лагранжа, мы должны найти минимум лагранжиана $L$ , который выражается как:

L=x+y+z+\lambda _{1}(x^{2}+y^{2}-2xy\cos(\alpha )-a^{2})+\lambda _{2}(y^{2}+z^{2}-2yz\cos(\beta )-b^{2})+\lambda _{3}(z^{2}+x^{2}-2zx\cos(\alpha +\beta )-c^{2})

где $a, b, c$ — длины сторон треугольника.

Приравнивая каждую из пяти частных производных к нулю и исключая $λ$ $1$ $,$ $λ$ $2$ $,$ $λ$ $3 ,$ в конечном итоге получаем $sin$ $α$ $= sin$ $β$ и $sin($ $α$ $+$ $β$ $) = - sin$ $β$ , так что $α$ $=$ $β$ $= 120°$ . Однако исключение — долгое и утомительное дело, и конечный результат охватывает только Случай 2. ${\tfrac {\partial L}{\partial x}},{\tfrac {\partial L}{\partial y}},{\tfrac {\partial L}{\partial z}},{\tfrac {\partial L}{\partial \alpha }},{\tfrac {\partial L}{\partial \beta }}$

Характеристики

Если наибольший угол треугольника не больше 120°, то X (13) является точкой Ферма.
Углы, образованные сторонами треугольника в точке X (13), все равны 120° (случай 2) или 60°, 60°, 120° (случай 1).
Описанные окружности трех построенных равносторонних треугольников пересекаются в точке X (13).
Трилинейные координаты для первого изогонического центра, X (13): ^[3]

{\begin{aligned}&\csc \left(A+{\tfrac {\pi }{3}}\right):\csc \left(B+{\tfrac {\pi }{3}}\right):\csc \left(C+{\tfrac {\pi }{3}}\right)\\&=\sec \left(A-{\tfrac {\pi }{6}}\right):\sec \left(B-{\tfrac {\pi }{6}}\right):\sec \left(C-{\tfrac {\pi }{6}}\right).\end{aligned}}

Трилинейные координаты для второго изогонического центра, X (14): ^[4]

{\begin{aligned}&\csc \left(A-{\tfrac {\pi }{3}}\right):\csc \left(B-{\tfrac {\pi }{3}}\right):\csc \left(C-{\tfrac {\pi }{3}}\right)\\&=\sec \left(A+{\tfrac {\pi }{6}}\right):\sec \left(B+{\tfrac {\pi }{6}}\right):\sec \left(C+{\tfrac {\pi }{6}}\right).\end{aligned}}

Трилинейные координаты точки Ферма:

1-u+uvw\sec \left(A-{\tfrac {\pi }{6}}\right):1-v+uvw\sec \left(B-{\tfrac {\pi }{6}}\right):1-w+uvw\sec \left(C-{\tfrac {\pi }{6}}\right)

где

u, v, w

обозначают соответственно булевы переменные

(A < 120°), (B < 120°), (C < 120°)

Изогональное сопряжение X (13) — это первая изодинамическая точка X (15): ^[5]

\sin \left(A+{\tfrac {\pi }{3}}\right):\sin \left(B+{\tfrac {\pi }{3}}\right):\sin \left(C+{\tfrac {\pi }{3}}\right).

Изогональное сопряжение X (14) — это вторая изодинамическая точка X (16): ^[6]

\sin \left(A-{\tfrac {\pi }{3}}\right):\sin \left(B-{\tfrac {\pi }{3}}\right):\sin \left(C-{\tfrac {\pi }{3}}\right).

Следующие треугольники являются равносторонними:
- антипедальный треугольник X ( 13)
- Антипедальный треугольник X (14)
- Педальный треугольник X (15)
- Педальный треугольник X (16)
- Описанный треугольник X ( 15)
- Описанный треугольник X (16)
Прямые X (13) X (15) и X (14) X (16) параллельны прямой Эйлера . Три прямые пересекаются в точке бесконечности Эйлера, X (30).
Точки X (13), X (14), центр описанной окружности и центр девяти точек лежат на окружности Лестера .
Линия X (13) X (14) пересекает линию Эйлера в средней точке X (2) и X (4). ^[7]
Точка Ферма лежит в открытом ортоцентроидальном диске, проколотом в его собственном центре, и может быть любой точкой в нем. ^[8]

Псевдонимы

Изогонические центры X (13) и X (14) также известны как первая точка Ферма и вторая точка Ферма соответственно. Альтернативами являются положительная точка Ферма и отрицательная точка Ферма . Однако эти разные названия могут сбивать с толку и, возможно, их лучше избегать. Проблема в том, что большая часть литературы размывает различие между точкой Ферма и первой точкой Ферма , тогда как только в случае 2 выше они фактически одинаковы.

История

Этот вопрос был предложен Ферма, как вызов Эванджелисте Торричелли . Он решил задачу аналогично Ферма, хотя и использовал пересечение описанных окружностей трех правильных треугольников. Его ученик Вивиани опубликовал решение в 1659 году. ^[9]

Смотрите также

Геометрическая медиана или точка Ферма–Вебера — точка, минимизирующая сумму расстояний до более чем трех заданных точек.
Теорема Лестера
Треугольный центр
Наполеон указывает
проблема Вебера

Ссылки

^ Разрубить узел - Точка Ферма и обобщения
^ Кимберлинг, Кларк (1994). «Центральные точки и центральные линии в плоскости треугольника». Mathematics Magazine . 67 (3): 163–187. doi :10.1080/0025570X.1994.11996210. JSTOR 2690608. MR 1573021.См. X ₁₃ , стр. 174.
↑ Запись X(13) в Энциклопедии центров треугольников, архивирована 19 апреля 2012 г. на Wayback Machine.
↑ Запись X(14) в Энциклопедии центров треугольников, архивирована 19 апреля 2012 г. на Wayback Machine.
↑ Запись X(15) в Энциклопедии центров треугольников, архив 19 апреля 2012 г., на Wayback Machine
↑ Запись X(16) в Энциклопедии центров треугольников, архивирована 19 апреля 2012 г. на Wayback Machine.
^ Кимберлинг, Кларк. «Энциклопедия треугольных центров».
^ Кристофер Дж. Брэдли и Джефф К. Смит, «Расположение центров треугольников», Forum Geometricorum 6 (2006), 57--70. http://forumgeom.fau.edu/FG2006volume6/FG200607index.html
^ Вайсштейн, Эрик В. «Точки Ферма». MathWorld .

Внешние ссылки

«Задача Ферма-Торричелли», Энциклопедия математики , EMS Press , 2001 [1994]
Точка Ферма Криса Буше, проект «Демонстрации Вольфрама» .
Обобщение Ферма-Торричелли в зарисовках динамической геометрии Интерактивный зарисовок обобщает точку Ферма-Торричелли.
Практический пример точки Ферма