Джон Уоллис

Английский математик (1616–1703)

Джон Уоллис ( / ˈ w ɒ l ɪ s / ; [ ^2] лат . Wallisius ; 3 декабря [ OS 23 ноября] 1616 — 8 ноября [ OS 28 октября] 1703) — английский священнослужитель и математик , которому отчасти приписывают разработку исчисления бесконечно малых .

Между 1643 и 1689 годами Уоллис служил главным криптографом парламента , а позднее — королевского двора. ^[3] Ему приписывают введение символа ∞ для обозначения понятия бесконечности . ^[4] Он также использовал 1/∞ для обозначения бесконечно малых величин . Он был современником Ньютона и одним из величайших интеллектуалов раннего возрождения математики . ^[5]

Биография

Образование

• Кембридж, Массачусетс, Оксфорд, ДД
• Гимназия в Тентердене, Кент, 1625–1631 гг.
• Школа Мартина Гольбича в Фелстеде, Эссекс, 1631–1632 гг.
• Кембриджский университет, Эммануэль-колледж, 1632–1640; бакалавр искусств, 1637; магистр искусств, 1640.
• DD в Оксфорде в 1654 году

Семья

14 марта 1645 года он женился на Сюзанне Глайнд ( ок.  1600 – 16 марта 1687). У них было трое детей:

1. Энн, леди Бленкоу (4 июня 1656 г. – 5 апреля 1718 г.), вышла замуж за сэра Джона Бленкоу (30 ноября 1642 г. – 6 мая 1726 г.) в 1675 г., у них было потомство ^[6]
2. Джон Уоллис (26 декабря 1650 г. – 14 марта 1717 г.), ^[7] депутат парламента от Уоллингфорда в 1690–1695 гг., женился на Элизабет Харрис (ум. 1693 г.) 1 февраля 1682 г., дети: сын и две дочери
3. Элизабет Уоллис (1658–1703 ^[8] ), вышла замуж за Уильяма Бенсона (1649–1691) из Таустера, умерла, не оставив потомства

Жизнь

Джон Уоллис родился в Эшфорде, Кент . Он был третьим из пяти детей преподобного Джона Уоллиса и Джоанны Чепмен. Первоначально он получил образование в школе в Эшфорде, но в 1625 году после вспышки чумы перешел в школу Джеймса Мовата в Тентердене . Уоллис впервые познакомился с математикой в ​​1631 году в школе Фелстеда (тогда известной как школа Мартина Холбича в Фелстеде); ему нравилась математика, но его обучение было нерегулярным, поскольку «математика в то время у нас редко рассматривалась как академическое занятие, а скорее как механическое» (Scriba 1970). В школе в Фелстеде Уоллис научился говорить и писать на латыни . К этому времени он также свободно владел французским , греческим и ивритом . ^[9] Поскольку предполагалось, что он должен был стать врачом, в 1632 году его отправили в колледж Эммануэля в Кембридже . ^[10] Там он вел акт о учении о кровообращении ; говорят, что это был первый случай в Европе, когда эта теория была публично поддержана в диспуте. Однако его интересы были сосредоточены на математике. Он получил степень бакалавра искусств в 1637 году и степень магистра в 1640 году, после чего вступил в сан священника. С 1643 по 1649 год он служил неголосующим писцом в Вестминстерской ассамблее . Он был избран в стипендию в Куинс-колледже в Кембридже в 1644 году, из которого он был вынужден уйти после женитьбы. ^{[ необходима цитата ]}

В течение всего этого времени Уоллис был близок к парламентской партии, возможно, из-за его контактов с Гольбичем в школе Фельстеда. Он оказал им большую практическую помощь в расшифровке роялистских депеш. Качество криптографии в то время было неоднозначным; несмотря на индивидуальные успехи таких математиков, как Франсуа Виет , принципы, лежащие в основе разработки и анализа шифров, были очень плохо поняты. Большинство шифров были методами ad hoc, полагающимися на секретный алгоритм , в отличие от систем, основанных на переменном ключе . Уоллис понял, что последние были гораздо более безопасными, - даже описывая их как «невзламываемые», хотя он не был достаточно уверен в этом утверждении, чтобы поощрять раскрытие криптографических алгоритмов. Он также был обеспокоен использованием шифров иностранными державами, отклонив, например, просьбу Готфрида Лейбница от 1697 года обучить ганноверских студентов криптографии. ^[11]

Вернувшись в Лондон — в 1643 году он был назначен капелланом в церкви Св. Гавриила Фенчерча — Уоллис присоединился к группе ученых, которая позже превратилась в Королевское общество . Он, наконец, смог удовлетворить свои математические интересы, освоив Clavis Mathematicae Уильяма Отреда за несколько недель в 1647 году. Вскоре он начал писать собственные трактаты, затрагивая широкий круг тем, что он продолжал делать до конца своей жизни. Уоллис написал первый обзор математических концепций в Англии, где он обсуждал индо-арабскую систему. ^[12]

Уоллис присоединился к умеренным пресвитерианам, подписав протест против казни Карла I , чем вызвал длительную враждебность со стороны независимых. Несмотря на их сопротивление, в 1649 году он был назначен на кафедру геометрии Сэвилиан в Оксфордском университете, где и прожил до своей смерти 8 ноября [ OS 28 October] 1703 года. В 1650 году Уоллис был рукоположен в священники. После этого он провел два года с сэром Ричардом Дарли и леди Вер в качестве частного капеллана . В 1661 году он был одним из двенадцати пресвитерианских представителей на Савойской конференции . ^{[ необходима цитата ]}

Помимо своих математических работ он писал по теологии , логике , английской грамматике и философии, а также участвовал в разработке системы обучения глухого мальчика говорению в Littlecote House . ^{[13] Ранее} Уильям Холдер научил глухого мужчину, Александра Попхэма, говорить «ясно и отчетливо, и с хорошим и изящным тоном». ^[14] Позже Уоллис присвоил себе эту заслугу, что заставило Холдера обвинить Уоллиса в том, что он «обшаривает своих соседей и украшает себя их добычей». ^[15]

Назначение Уоллиса профессором геометрии в Оксфордском университете

Парламентский визит в Оксфорд , начавшийся в 1647 году, устранил многих старших академиков со своих должностей, включая в ноябре 1648 года профессоров геометрии и астрономии Сэвилиан. В 1649 году Уоллис был назначен профессором геометрии Сэвилиан. Уоллис, по-видимому, был выбран в основном по политическим мотивам (как, возможно, и его предшественник-роялист Питер Тернер , который, несмотря на назначение на две профессорские должности, так и не опубликовал ни одной математической работы); хотя Уоллис был, возможно, ведущим криптографом страны и входил в неформальную группу ученых, которая позже стала Королевским обществом , у него не было особой репутации как математика. Тем не менее, назначение Уоллиса оказалось в полной мере оправданным его последующей работой в течение 54 лет, которые он прослужил профессором Сэвилиан. ^[16]

Вклад в математику

Опера Математика , 1699

Валлис внес значительный вклад в тригонометрию , исчисление , геометрию и анализ бесконечных рядов . В своей Opera Mathematica I (1695) он ввел термин « непрерывная дробь ».

Аналитическая геометрия

В 1655 году Валлис опубликовал трактат о конических сечениях , в котором они были определены аналитически. Это была самая ранняя книга, в которой эти кривые рассматривались и определялись как кривые второй степени . Она помогла устранить некоторые из кажущихся трудностей и неясностей работы Рене Декарта по аналитической геометрии .

В «Трактате о конических сечениях » Уоллис популяризировал символ ∞ для обозначения бесконечности. Он писал: «Я предполагаю, что любая плоскость (следуя геометрии неделимых Кавальери) состоит из бесконечного числа параллельных линий или, как я бы предпочел, из бесконечного числа параллелограммов одинаковой высоты; (пусть высота каждого из них будет бесконечно малой частью 1/∞ всей высоты, и пусть символ ∞ обозначает бесконечность) и высота всех их составит высоту фигуры». ^[17]

Интегральное исчисление

Arithmetica Infinitorum , важнейшая из работ Уоллиса, была опубликована в 1656 году. В этом трактате были систематизированы и расширены методы анализа Декарта и Кавальери , но некоторые идеи были открыты для критики. Он начал, после короткого трактата о конических сечениях, с разработки стандартной нотации для степеней, распространив их с положительных целых чисел на рациональные числа :

${\displaystyle x^{0}=1}$

${\displaystyle x^{-1}={\frac {1}{x}}}$

${\displaystyle x^{-n}={\frac {1}{x^{n}}}{\text{ etc.}}}$

${\displaystyle x^{1/2}={\sqrt {x}}}$

${\displaystyle x^{2/3}={\sqrt[{3}]{x^{2}}}{\text{ etc.}}}$

${\displaystyle x^{1/n}={\sqrt[{n}]{x}}}$

${\displaystyle x^{p/q}={\sqrt[{q}]{x^{p}}}}$

Оставив многочисленные алгебраические приложения этого открытия, он затем приступил к поиску, путем интегрирования , площади, заключенной между кривой y = x ^m , осью x и любой ординатой x = h , и доказал, что отношение этой площади к площади параллелограмма на том же основании и той же высоты равно 1/( m  + 1), расширяя квадратурную формулу Кавальери . Он, по-видимому, предполагал, что тот же результат будет верен и для кривой y = ax ^m , где a — любая константа, а m — любое число, положительное или отрицательное, но он обсуждал только случай параболы , в которой m = 2, и гиперболы, в которой m = −1. В последнем случае его интерпретация результата неверна. Затем он показал, что аналогичные результаты можно записать для любой кривой вида

${\displaystyle y=\sum _{m}^{}ax^{m}}$

и, следовательно, если ординату y кривой можно разложить по степеням x , то можно определить ее площадь: так, он говорит, что если уравнение кривой имеет вид y = x ⁰ + x ¹ + x ² + ..., то ее площадь будет равна x + x ² /2 + x ³ /3 + ... . Затем он применил это к квадратуре кривых y = ( x − x ² ) ⁰ , y = ( x − x ² ) ¹ , y = ( x − x ² ) ² и т. д., взятых между пределами x  = 0 и x  = 1. Он показывает, что площади равны соответственно 1, 1/6, 1/30, 1/140 и т. д. Затем он рассмотрел кривые вида y = x ^{1/ m} и установил теорему о том, что площадь, ограниченная этой кривой и линиями x  = 0 и x  = 1, равна площади прямоугольника на том же основании и той же высоте, что и m  : m  + 1. Это эквивалентно вычислению

${\displaystyle \int _{0}^{1}x^{1/m}\,dx.}$

Он проиллюстрировал это с помощью параболы, в этом случае m = 2. Он сформулировал, но не доказал, соответствующий результат для кривой вида y = x ^{p / q} .

Уоллис проявил значительную изобретательность в приведении уравнений кривых к формам, данным выше, но, поскольку он не был знаком с биномиальной теоремой , он не мог осуществить квадратуру окружности , уравнение которой имеет вид , поскольку он не мог разложить его по степеням x . Однако он установил принцип интерполяции . Таким образом, поскольку ордината окружности является геометрическим средним ординат кривых и , можно было бы предположить, что в качестве приближения площадь полукруга , которая равна , может быть взята как геометрическое среднее значений ${\displaystyle y={\sqrt {1-x^{2}}}}$ ${\displaystyle y={\sqrt {1-x^{2}}}}$ ${\displaystyle y=(1-x^{2})^{0}}$ ${\displaystyle y=(1-x^{2})^{1}}$ ${\displaystyle \int _{0}^{1}\!{\sqrt {1-x^{2}}}\,dx}$ ${\displaystyle {\tfrac {1}{4}}\pi }$

${\displaystyle \int _{0}^{1}(1-x^{2})^{0}\,dx\ {\text{ and }}\int _{0}^{1}(1-x^{2})^{1}\,dx,}$

то есть, и ; это эквивалентно принятию или 3,26... в качестве значения π. Но, утверждал Уоллис, на самом деле у нас есть ряд ... и поэтому член, интерполированный между и, должен быть выбран так, чтобы подчиняться закону этого ряда. ^{[ необходимо разъяснение ]} Это, с помощью сложного метода, который здесь подробно не описан, приводит к значению для интерполированного члена, которое эквивалентно принятию ${\displaystyle 1}$ ${\displaystyle {\tfrac {2}{3}}}$ ${\displaystyle 4{\sqrt {\tfrac {2}{3}}}}$ ${\displaystyle 1,{\tfrac {1}{6}},{\tfrac {1}{30}},{\tfrac {1}{140}},}$ ${\displaystyle 1}$ ${\displaystyle {\tfrac {1}{6}}}$

${\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdots }$

(который теперь известен как продукт Уоллиса ).

В этой работе также обсуждаются образование и свойства непрерывных дробей , поскольку эта тема приобрела известность благодаря использованию этих дробей Брункером .

Несколько лет спустя, в 1659 году, Уоллис опубликовал трактат, содержащий решение задач на циклоиду , предложенных Блезом Паскалем . В нем он попутно объяснил, как принципы, изложенные в его Arithmetica Infinitorum, могут быть использованы для выпрямления алгебраических кривых, и дал решение задачи по выпрямлению (т. е. нахождению длины) полукубической параболы x ³ = ay ² , открытой в 1657 году его учеником Уильямом Нейлом . Поскольку все попытки выпрямить эллипс и гиперболу были (обязательно) безрезультатными, предполагалось, что никакие кривые не могут быть выпрямлены, как, собственно, и утверждал Декарт. Логарифмическая спираль была выпрямлена Эванджелистой Торричелли и была первой кривой линией (кроме окружности), длина которой была определена, но расширение Нилом и Уоллисом до алгебраической кривой было новым. Циклоида была следующей выпрямленной кривой; это сделал Кристофер Рен в 1658 году. ^{[ необходима цитата ]}

В начале 1658 года аналогичное открытие, независимое от открытия Нейла, сделал ван Хейраэт , и оно было опубликовано ван Схутеном в его издании «Геометрии» Декарта в 1659 году. Метод ван Хейраэта заключается в следующем. Он предполагает, что кривая отнесена к прямоугольным осям; если это так, и если ( x , y ) — координаты любой точки на ней, а n — длина нормали, ^{[ необходимо разъяснение ]} и если другая точка с координатами ( x , η ) взята так, что η  : h = n  : y , где h — константа; тогда, если ds — элемент длины искомой кривой, то посредством подобных треугольников мы имеем ds  : dx = n  : y . Следовательно, h ds = η dx . Следовательно, если площадь геометрического места точки ( x , η ) может быть найдена, то первая кривая может быть выпрямлена. Таким образом, ван Хейраэт осуществил выпрямление кривой y ³ = ax ^{2 ,} но добавил, что выпрямление параболы y ² = ax невозможно, поскольку оно требует квадратуры гиперболы. Решения, данные Нейлом и Уоллисом, несколько похожи на решения, данные ван Хейраэтом, хотя общее правило не сформулировано, а анализ неуклюж. Третий метод был предложен Ферма в 1660 году, но он неэлегантный и трудоемкий.

Столкновение тел

Теория столкновения тел была предложена Королевским обществом в 1668 году для рассмотрения математиками. Уоллис, Кристофер Рен и Христиан Гюйгенс прислали правильные и похожие решения, все основанные на том, что сейчас называется сохранением импульса ; но, в то время как Рен и Гюйгенс ограничили свою теорию совершенно упругими телами ( упругое столкновение ), Уоллис также рассматривал несовершенно упругие тела ( неупругое столкновение ). За этим в 1669 году последовала работа по статике (центры тяжести), а в 1670 году — по динамике : они дают удобный синопсис того, что тогда было известно по этому вопросу.

Алгебра

В 1685 году Уоллис опубликовал «Алгебру» , которой предшествовал исторический отчет о развитии предмета, содержащий много ценной информации. Второе издание, выпущенное в 1693 году и составившее второй том его «Оперы» , было значительно расширено. Эта алгебра примечательна тем, что содержит первое систематическое использование формул. Данная величина здесь представлена ​​числовым отношением, которое она имеет к единице того же рода величины: таким образом, когда Уоллис хочет сравнить две длины, он рассматривает каждую как содержащую столько-то единиц длины. Это, возможно, станет яснее, если заметить, что соотношение между пространством, описываемым в любой момент времени частицей, движущейся с постоянной скоростью, Уоллис обозначает формулой

с = vt ,

где s — число, представляющее отношение описываемого пространства к единице длины; в то время как предыдущие авторы обозначили бы то же самое отношение, указав, что эквивалентно предложению

с1  : с2 = v1 t1  : v2 _t2 ._​​​​​_​

Числовая прямая

Говоря о движении вперед и отступлении от точки , Уоллис в «Трактате по алгебре» писал , что «... так же верно проектирует Точку , как проектировал Точку ... И каждый проектирует (по крайней мере, в той же Бесконечной Линии) одну Единственную Точку: И только одну». ${\displaystyle A}$ ${\displaystyle -3}$ ${\displaystyle D}$ ${\displaystyle +3}$ ${\displaystyle C}$ 

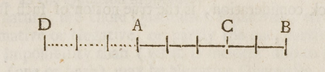
Уоллис считается создателем числовой прямой «для отрицательных величин» ^[18] и «для операциональных целей». ^[19] Это основано на отрывке из его трактата по алгебре 1685 года, в котором он ввел числовую прямую для иллюстрации законности отрицательных величин: ^[20]

Однако это предположение (отрицательных величин) не является ни бесполезным, ни абсурдным; если его правильно понимать. И хотя, что касается голой алгебраической нотации, оно подразумевает величину, меньшую, чем ничто: Однако, когда дело доходит до физического применения, оно обозначает как реальную величину, как если бы знак был ; но если его интерпретировать в противоположном смысле... , означает ярды вперед; а , означает ярды назад. ${\displaystyle +}$ ${\displaystyle +3}$ ${\displaystyle 3}$ ${\displaystyle -3}$ ${\displaystyle 3}$

Было отмечено, что в более ранней работе Уоллис пришел к выводу, что отношение положительного числа к отрицательному больше бесконечности. Аргумент включает в себя частное и рассмотрение того, что происходит при приближении и пересечении точки с положительной стороны. ^[21] Уоллис был не одинок в своих размышлениях: Леонард Эйлер пришел к такому же выводу, рассматривая геометрическую прогрессию , оцененную при , а затем рассуждая аналогично Уоллису (он разрешил парадокс, различая различные виды отрицательных чисел). ^[18] ${\displaystyle {\tfrac {1}{x}}}$ ${\displaystyle x}$ ${\displaystyle x=0}$ ${\displaystyle {\tfrac {1}{1-x}}=1+x+x^{2}+\cdots }$ ${\displaystyle x=2}$

Геометрия

Обычно ему приписывают доказательство теоремы Пифагора с использованием подобных треугольников . Однако Сабит ибн Курра (901 г. н. э.), арабский математик, шестью веками ранее создал обобщение теоремы Пифагора, применимое ко всем треугольникам. Разумно предположить, что Уоллис был знаком с работой Сабита. ^[22]

Уоллис также был вдохновлен работами исламского математика Садра аль-Туси, сына Насира ад-Дина аль-Туси , в частности книгой аль-Туси, написанной в 1298 году о постулате о параллельных линиях . Книга была основана на мыслях его отца и представляла один из самых ранних аргументов в пользу неевклидовой гипотезы, эквивалентной постулату о параллельных линиях. Прочитав это, Уоллис затем написал о своих идеях, поскольку он развивал свои собственные мысли о постулате, пытаясь доказать его также с помощью подобных треугольников. ^[23]

Он обнаружил, что пятый постулат Евклида эквивалентен постулату, который в настоящее время называется «постулатом Уоллиса» в его честь. Этот постулат гласит, что «На данной конечной прямой всегда можно построить треугольник, подобный данному треугольнику». Этот результат был включен в тенденцию, пытающуюся вывести пятый постулат Евклида из остальных четырех постулатов, что сегодня известно как невозможное. В отличие от других авторов, он понял, что неограниченный рост треугольника не гарантируется четырьмя первыми постулатами. ^[24]

Калькулятор

Другим аспектом математических навыков Уоллиса была его способность производить устные вычисления. Он плохо спал и часто делал устные вычисления, лежа без сна в своей постели. Однажды ночью он вычислил в уме квадратный корень числа с 53 цифрами. Утром он продиктовал 27-значный квадратный корень числа, все еще полностью по памяти. Это был подвиг, который считался выдающимся, и Генри Ольденбург , секретарь Королевского общества, послал коллегу, чтобы выяснить, как Уоллис это сделал. Это было сочтено достаточно важным, чтобы заслужить обсуждение в Philosophical Transactions of the Royal Society 1685 года. ^{[25] [26]}

Теория музыки

Уоллис перевел на латынь труды Птолемея и Вриенния, а также комментарий Порфирия к Птолемею. Он также опубликовал три письма Генри Ольденбургу относительно настройки. Он одобрил равномерную темперацию , которая использовалась в органах Англии. ^[27]

Другие работы

Опера Математика , 1657

Его Institutio logicae , опубликованный в 1687 году, был очень популярен. ^[4] Grammatica linguae Anglicanae была работой по английской грамматике , которая оставалась в печати вплоть до восемнадцатого века. Он также публиковал работы по теологии. ^[4]

Уоллис как криптограф

Работая капелланом леди Вир в 1642 году, Уоллис получил зашифрованное письмо о падении Чичестера , которое он сумел расшифровать в течение двух часов. Это положило начало его карьере криптографа. Он был умеренным сторонником парламентской стороны в Первой гражданской войне в Англии и поэтому работал расшифровщиком перехваченной корреспонденции для лидеров парламента. За свои услуги он был вознагражден житиями Святого Гавриила и Святого Мартина в Лондоне . ^[28]

Из-за своих парламентских симпатий Уоллис не был нанят в качестве криптографа после Реставрации Стюартов , ^[29] но после Славной революции его разыскал лорд Ноттингем и часто нанимал для расшифровки зашифрованной перехваченной корреспонденции, хотя он считал, что не всегда получал адекватное вознаграждение за свою работу. ^[a] Король Вильгельм III с 1689 года также нанимал Уоллиса в качестве криптографа, иногда почти ежедневно. Курьеры приносили ему письма для расшифровки и ждали перед его кабинетом результат. Король проявлял личный интерес к работе и благополучию Уоллиса, о чем свидетельствует письмо, которое он отправил голландскому великому пенсионарию Энтони Хейнсиусу в 1689 году. ^[29]

В эти ранние дни правления Вильгельма получение перехваченных иностранных писем было проблемой для англичан, поскольку у них еще не было ресурсов иностранных Черных палат , но союзники, такие как курфюрст Бранденбургский, не имевшие собственных Черных палат, время от времени делали подарки в виде перехваченной корреспонденции, как, например, письмо короля Франции Людовика XIV королю Польши Яну III Собескому , которое король Вильгельм в 1689 году использовал, чтобы вызвать кризис во франко-польских дипломатических отношениях. Он был довольно открыт в этом, и Уоллис был вознагражден за свою роль. ^[31] Но Уоллис занервничал, что французы могут предпринять против него действия. ^[32]

Отношения Валлиса с немецким математиком Готфридом Вильгельмом Лейбницем были сердечными. Но Лейбниц также интересовался криптографией и пытался заставить Валлиса раскрыть некоторые из его торговых секретов, что Валлис отказался сделать из патриотических принципов. ^[33]

Смит приводит пример кропотливой работы, проделанной Уоллисом, описанный им самим в письме Ричарду Хэмпдену от 3 августа 1689 года. В нем он дает подробный отчет о своей работе над конкретным письмом и о тех частях, с которыми он столкнулся. ^[34]

Переписка Уоллиса также показывает подробности того, как он защищал себя, когда считал, что его недооценивают, финансово или иным образом. Он с энтузиазмом лоббировал как от своего имени, так и от имени своих родственников, о чем свидетельствуют письма лорду Ноттингему, Ричарду Хэмпдену и депутату Харборду Харборду , которые цитирует Смит. ^[35] В письме английскому посланнику в Пруссии Джеймс Джонстон Уоллис горько жалуется, что придворный прусского курфюрста по имени Смето поступил с ним несправедливо в вопросе справедливой компенсации за услуги, оказанные курфюрсту. В письме он приводит подробности того, что он сделал, и дает советы по простому подстановочному шифру для использования самим Джонстоном. ^[36]

Вклад Уоллиса в искусство криптографии носил не только «технологический» характер. Де Леу отмечает, что даже «чисто научный» вклад Уоллиса в науку лингвистики в области «рациональности» естественного языка , как он развивался с течением времени, сыграл роль в развитии криптологии как науки. Разработка Уоллисом модели английской грамматики, независимой от более ранних моделей, основанных на латинской грамматике, является примером того, как другие науки помогли развить криптологию, по его мнению. ^[37]

Уоллис пытался научить своего сына Джона и внука от дочери Энн, Уильяма Бленкоу, приемам ремесла. С Уильямом он был настолько успешен, что смог убедить правительство разрешить внуку получать ежегодную пенсию в размере 100 фунтов стерлингов , которую Уоллис получал в качестве компенсации за свою криптографическую работу. ^[38]

Уильям Бленкоу в конечном итоге стал преемником Уоллиса на посту официального криптографа королевы Анны после его смерти в 1703 году. ^[39]

Смотрите также

• 31982 Джонваллис , астероид, названный в его честь
• Невидимый колледж
• John Wallis Academy — бывшая школа ChristChurch в Эшфорде, переименованная в 2010 году.
• Конический край Уоллиса
• Интегралы Уоллиса

Примечания

1. Смит цитирует его порой язвительные письма Ноттингему и другим. ^[30]

Ссылки

1. Джозеф Фредерик Скотт, Математические работы Джона Уоллиса (1616-1703) , Тейлор и Фрэнсис, 1938, стр. 109.
2. Словарь Random House.
3. Смит, Дэвид Юджин (1917). «Джон Уоллис как криптограф». Бюллетень Американского математического общества . 24 (2): 82–96. doi : 10.1090/s0002-9904-1917-03015-7 . MR  1560009.
4. Чисхолм, Хью , ред. (1911). "Уоллис, Джон"  . Encyclopaedia Britannica . Том 28 (11-е изд.). Cambridge University Press. стр. 284–285.
5. Кернс, ДА (1958). «Джон Уоллис и комплексные числа». Учитель математики . 51 (5): 373–374. JSTOR  27955680.
6. Джоан Тёрск (2005). «Бленкоу, Энн, леди Бленкоу (1656–1718)». Оксфордский национальный биографический словарь . Оксфордский национальный биографический словарь (онлайн-ред.). Oxford University Press. doi :10.1093/ref:odnb/41326 . Получено 21 августа 2023 г. . (Требуется подписка или членство в публичной библиотеке Великобритании.)
7. "УОЛЛИС, Джон (1650-1717), из Саунднесса, Неттлбед, Оксон". История парламента онлайн . Получено 21 августа 2023 г.
8. "Элизабет Уоллис". Early Modern Letters Online : Person . Получено 21 августа 2023 г.
9. Юл, Г. Удни (1939). «Джон Уоллис, DD, FRS». Заметки и записи Лондонского королевского общества . 2 (1): 74–82. doi :10.1098/rsnr.1939.0012. JSTOR  3087253.
10. "Уоллис, Джон (WLS632J)". База данных выпускников Кембриджа . Кембриджский университет.
11. Кан, Дэвид (1967), Дешифровщики: История тайнописи , Нью-Йорк: Macmillan, стр. 169, LCCN  63016109
12. 4
13. «Находка может положить конец 350-летнему научному спору». BBC. 26 июля 2008 г. Получено 5 мая 2018 г.
14. W. Holder, W. (1668). «Об эксперименте, касающемся глухоты». Philosophical Transactions of the Royal Society 3, стр. 665–668.
15. Холдер, Философские труды Королевского общества , приложение, 10.
16. Джон Уоллис: Хронология, maths.ox.ac.uk. Доступ 19 апреля 2024 г.
17. Скотт, Дж. Ф. 1981. Математические работы Джона Уоллиса, доктора богословия, члена Королевского общества (1616–1703) . Chelsea Publishing Co., Нью-Йорк, штат Нью-Йорк. стр. 18.
18. Heeffer, Albrecht (10 марта 2011 г.). «Исторические возражения против числовой прямой». Наука и образование . 20 (9): 863–880 [872–876]. Bibcode :2011Sc&Ed..20..863H. doi :10.1007/s11191-011-9349-0. hdl : 1854/LU-1891046 . S2CID  120058064.
19. Нуньес, Рафаэль (2017). «Насколько математика «зашита», если она вообще есть: биологическая эволюция, развитие и существенная роль культуры» (PDF) . В Sera, Maria D.; Carlson, Stephanie M.; Maratsos, Michael (ред.). Симпозиум по детской психологии в Миннесоте: системы культуры и развития, том 38 . John Wiley & Sons, Inc. стр. 83–124 [96]. doi :10.1002/9781119301981.ch3.
20. Уоллис, Джон (1685). Трактат по алгебре, как исторической, так и практической. Лондон: Ричард Дэвис. С. 265. MPIWG:GK8U243K.
21. Мартинес, Альберто А. (2006). Отрицательная математика: как математические правила могут быть положительно сложены. Princeton University Press. стр. 22. ISBN 978-0-691-12309-7. Получено 9 июня 2013 г.
22. Джозеф, ГГ (2000). Гребень павлина: неевропейские корни математики (2-е изд.). Penguin. стр. 337. ISBN 978-0-14-027778-4.
23. Математика Египта, Месопотамии, Китая, Индии и ислама: Справочник Виктор Дж. Кац Издательство Принстонского университета Архивировано 1 октября 2016 г. на Wayback Machine
24. Бертон, Дэвид М. (2011), История математики / Введение (7-е изд.), McGraw-Hill, стр. 566, ISBN 978-0-07-338315-6
25. Доктор Уоллис (1685) «Два отрывка из журнала Фил. общества Оксфорда; один содержит статью, переданную 31 марта 1685 года преподобным доктором Уоллисом, президентом этого общества, относительно силы памяти, применяемой с должным вниманием; …», Philosophical Transactions of the Royal Society of London , 15  : 1269-1271. Доступно в сети по адресу: Royal Society of London ^{[ постоянная нерабочая ссылка ]}
26. Хоппен, К. Теодор (2013), Обычный ученый семнадцатого века: исследование Дублинского философского общества, 1683–1708, Routledge Library Editions: История и философия науки, т. 15, Routledge, стр. 157, ISBN 9781135028541
27. Дэвид Дамшодер и Дэвид Рассел Уильямс, Теория музыки от Царлино до Шенкера: Библиография и руководство (Стайтвесант, Нью-Йорк: Pendragon Press, 1990), стр. 374.
28. Смит, стр. 83
29. De Leeuw (1999), стр. 138
30. Смит, стр. 83-86
31. Смит, стр. 87
32. Де Леу (1999), стр. 139
33. Смит, стр. 83-84.
34. Смит, стр. 85-87
35. Смит, стр. 89-93.
36. Смит, стр. 94-96.
37. Де Леув (2000), стр. 9
38. Cave, E., ed. (1788). «Оригинальное письмо доктора Уоллиса с некоторыми подробностями его пенсии». The Gentleman's Magazine . 63 (июнь 1788 г.): 479–480 . Получено 20 августа 2023 г.
39. Де Леу (1999), стр.143

Источники

• Первоначальный текст этой статьи взят из общедоступного источника:
• WW Рауз Болл (1908). «Краткий обзор истории математики» (4-е изд.).
• Leeuw, K. de (1999). «Черная палата в Голландской республике во время войны за испанское наследство и ее последствий, 1707-1715» (PDF) . Исторический журнал . 42 (1): 133–156. doi :10.1017/S0018246X98008292. S2CID  162387765 . Получено 3 августа 2023 г. .
• Leeuw, K. de (2000). «Использование кодов и шифров в Голландской Республике, в основном в XVIII веке». Криптология и государственное управление в Голландской Республике (PDF) . Амстердам. С. 6–51 . Получено 4 августа 2023 г.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Смит, Дэвид Юджин (1917). «Джон Уоллис как криптограф». Бюллетень Американского математического общества . 24 (2): 82–96. doi : 10.1090/s0002-9904-1917-03015-7 . MR  1560009.
• Scriba, CJ (1970). «Автобиография Джона Уоллиса, члена Королевского общества». Заметки и записи Лондонского королевского общества . 25 : 17–46. doi :10.1098/rsnr.1970.0003. S2CID  145393357.
• Стедалл, Жаклин, 2005, «Arithmetica Infinitorum» в книге Айвора Граттана-Гиннесса « Значительные труды по западной математике» . Elsevier: 23–32.
• Гвиччардини, Никколо (2012) «Джон Уоллис как редактор математических трудов Ньютона», Заметки и записи Лондонского королевского общества 66(1): 3–17. Ссылка Jstor
• Стедалл, Жаклин А. (2001) «О нашей собственной нации: рассказ Джона Уоллиса о математическом обучении в средневековой Англии», Historia Mathematica 28: 73.
• Уоллис, Дж. (1691). Седьмое письмо, касающееся священной Троицы, вызванное вторым письмом от У. Дж. / Джона Уоллиса ... (Ранние английские книги онлайн). Лондон: Напечатано для Tho. Parkhurst ...

Внешние ссылки

• Переписка Джона Уоллиса в EMLO
• "Уоллис, Джон (1616-1703)"  . Национальный биографический словарь . Лондон: Smith, Elder & Co. 1885–1900.
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Джон Уоллис», Архив истории математики Мактьютора , Университет Сент-Эндрюс
• Страница проекта Галилео
• «Архивные материалы, касающиеся Джона Уоллиса». Национальный архив Великобритании .
• Портреты Джона Уоллиса в Национальной портретной галерее в Лондоне
• Работы Джона Уоллиса в Post-Reformation Digital Library
• Джон Уоллис (1685) Трактат алгебры - цифровое факсимиле, Библиотека Линды Холл
• Уоллис, Джон (1685). Трактат алгебры, как исторический, так и практический. Показывающий ее происхождение, прогресс и развитие от времени к времени и какими шагами она достигла той высоты, на которой находится сейчас. Оксфорд: Ричард Дэвис. doi :10.3931/e-rara-8842.
• Хатчинсон, Джон (1892). «Джон Уоллис»  . Люди Кента и кентишмены (подписное издание). Кентербери: Кросс и Джекман. С. 139–140.