Алфавитная система счисления — это тип системы счисления . Разработанная в классической античности , она процветала в раннем Средневековье . [1] В алфавитных системах счисления числа записываются с использованием символов алфавита , слоговой азбуки или другой системы письма . В отличие от акрофонических систем счисления , где число представлено первой буквой лексического названия числа, алфавитные системы счисления могут произвольно назначать буквы числовым значениям. Некоторые системы, включая арабскую , грузинскую и еврейскую , используют уже установленный алфавитный порядок . [1] Алфавитные системы счисления возникли из греческих цифр около 600 г. до н. э. и в значительной степени вымерли к 16 веку. [1] После развития позиционных систем счисления , таких как индо-арабские цифры , использование алфавитных систем счисления сократилось до преимущественно упорядоченных списков, пагинации , религиозных функций и гадательной магии. [1]
Первой засвидетельствованной алфавитной системой счисления является греческая алфавитная система (названная ионической или милетской системой из-за ее происхождения на западе Малой Азии ). Структура системы следует структуре египетских демотических цифр ; греческие буквы заменили египетские знаки. Первые примеры греческой системы датируются VI веком до н. э. и были написаны буквами архаичного греческого письма, использовавшегося в Ионии . [2]
Другие культуры, контактировавшие с Грецией, переняли эту числовую нотацию, заменив греческие буквы своей собственной письменностью; к ним относятся евреи в конце II века до н. э. Готический алфавит перенял свои собственные алфавитные цифры вместе с греческой письменностью. [3] В Северной Африке коптская система была разработана в IV веке н. э., [4] а система геэз в Эфиопии была разработана около 350 года н. э. [5] Обе были разработаны на основе греческой модели.
Арабы разработали свою собственную алфавитную систему счисления, абджадские цифры , в 7 веке нашей эры и использовали ее для математических и астрологических целей даже в 13 веке, намного позже введения индо -арабской системы счисления . [6] После принятия христианства армяне и грузины разработали свою алфавитную систему счисления в 4 или начале 5 века, в то время как в Византийской империи кириллические цифры и глаголица были введены в 9 веке. Алфавитные системы счисления были известны и использовались на севере, в Англии, Германии и России, на юге, в Эфиопии, на востоке, в Персии, и в Северной Африке от Марокко до Средней Азии. [ необходима цитата ]
К XVI веку нашей эры большинство алфавитных систем счисления вымерли или использовались мало, будучи вытесненными арабскими позиционными и западными цифрами в качестве обычных цифр в торговле и управлении по всей Европе и на Ближнем Востоке. [1]
Новейшие алфавитные системы цифр, используемые в настоящее время, все они позиционные, являются частью тактильных систем письма для людей с нарушением зрения . Несмотря на то, что шрифт Брайля 1829 года имел простую шифро-позиционную систему, скопированную с западных цифр с отдельным символом для каждой цифры, ранний опыт работы со студентами заставил его разработчика Луи Брайля упростить систему, сократив количество доступных шаблонов (символов) со 125 до 63, поэтому ему пришлось перепрофилировать дополнительный символ, чтобы обозначить буквы a–j как цифры. Помимо этой традиционной системы, еще одна была разработана во Франции в 20 веке, а еще одна — в США.
Алфавитная система счисления использует буквы алфавита в определенном порядке для обозначения цифр.
В греческом языке буквы назначаются соответствующим числам в следующих наборах: от 1 до 9, от 10 до 90, от 100 до 900 и т. д. Десятичные знаки представлены одним символом. По мере того, как алфавит заканчивается, более высокие числа представляются различными методами умножения. Однако, поскольку системы письма имеют разное количество букв, другие системы письма не обязательно группируют числа таким образом. Греческий алфавит состоит из 24 букв; три дополнительные буквы должны были быть включены, чтобы достичь 900. В отличие от греческого, 22 буквы еврейского алфавита позволяли выражать числа до 400. 28 согласных знаков арабского абджада могли представлять числа до 1000. Древние арамейские алфавиты имели достаточно букв, чтобы достичь 9000. В математических и астрономических рукописях использовались другие методы для представления больших чисел. Римские цифры и аттические цифры , обе из которых также были алфавитными системами счисления, со временем стали более лаконичными, но требовали от своих пользователей знания гораздо большего количества знаков. Акрофонические цифры не относятся к этой группе систем, поскольку их буквенно-цифровые обозначения не следуют порядку алфавита.
Эти различные системы не имеют единой объединяющей черты или особенности. Наиболее распространенной структурой является шифро-аддитивная с десятичной основой, с использованием мультипликативно-аддитивной структуризации для более высоких чисел или без нее. Исключения включают армянскую нотацию Ширакаци , которая является мультипликативно-аддитивной и иногда использует основу 1000, а также греческую и арабскую астрономические системы обозначений.
В таблицах ниже показаны алфавитно-цифровые конфигурации различных систем письма.
Греческие алфавитные цифры – «ионийские» или «милетские цифры» – (минускульные буквы)
Некоторые числа, представленные греческими буквами :
В еврейской письменности всего двадцать два согласных знака, поэтому числа можно выразить отдельными знаками только до 400. Более высокие сотни – 500, 600, 700, 800 и 900 – можно записать только с помощью различных кумулятивно-аддитивных комбинаций нижних сотен (направление письма – справа налево): [7]
Армянские числительные (минускульные буквы):
В отличие от многих алфавитных систем счисления, армянская система не использует умножение на 1000 или 10000 для выражения более высоких значений. Вместо этого более высокие значения были записаны полностью с использованием лексических цифр. [8]
По мере того, как алфавит заканчивался, для выражения более высоких чисел в разных системах использовались различные методы умножения. В греческой алфавитной системе для чисел, кратных 1000, знак хаста помещался слева под знаком цифры, чтобы указать, что его следует умножить на 1000. [9]
С помощью второго уровня мультипликативного метода – умножения на 10 000 – числовой набор мог быть расширен. Наиболее распространенный метод, используемый Аристархом , включал размещение числовой фразы над большим символом M (M = мириады = 10 000) для обозначения умножения на 10 000. [10] Этот метод мог выражать числа до 100 000 000 (10 8 ).
20 704 − (2 ⋅ 10 000 + 700 + 4) можно представить как:
Согласно отчету Паппа Александрийского , Аполлоний Пергский использовал другой метод. В нем цифры выше M = мириады = 10 000 представляли показатель степени 10 000. Число, которое нужно было умножить на M, записывалось после символа M. [11] Этот метод мог выразить 5 462 360 064 000 000 как:
Буквенные цифры отличались от слов особыми знаками, чаще всего горизонтальной чертой над числовой фразой, но иногда и точками, расположенными по обе стороны от нее. Последнее проявилось в греческом алфавите знаком хаста .
= 285
В эфиопских цифрах , известных как Geʽez , знаки имеют отметки как над ними, так и под ними, чтобы указать, что их значение является числовым. Эфиопские цифры являются исключением, где числовые знаки не являются буквами их письменности. Эта практика стала универсальной с 15-го века. [12]
Цифровые знаки эфиопских цифр со знаками как над, так и под буквами:
Направление цифр соответствует направлению системы письма. Написание слева направо в греческих, коптских, эфиопских, готских, армянских, грузинских, глаголических и кириллических алфавитных цифрах, а также в нотации Ширакаци. Написание справа налево встречается в еврейских и сирийских алфавитных цифрах, арабских цифрах абджад и фесских цифрах. [ необходима цитата ]
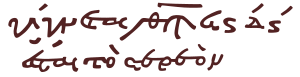
Единичные дроби были методом выражения дробей. В греческой алфавитной нотации единичные дроби обозначались знаменателем — буквенным цифровым знаком — за которым следовали небольшие акценты или штрихи, помещенные справа от цифры, известные как керайя (ʹ). Таким образом, γʹ обозначало одну треть, δʹ — одну четвертую и т. д. Эти дроби были аддитивными и также назывались египетскими дробями .
Например: δ´ ϛ´ = 1 ⁄ 4 + 1 ⁄ 6 = 5 ⁄ 12 .
Смешанное число можно записать так: ͵θϡϟϛ δ´ ϛ´ = 9996 + 1 ⁄ 4 + 1 ⁄ 6

Во многих астрономических текстах особый набор алфавитных систем счисления смешивает свои обычные алфавитные цифры с основанием 60, например, вавилонские шестидесятеричные системы . Во II веке до н. э. появился гибрид вавилонской нотации и греческих алфавитных цифр, который использовался для выражения дробей. [13] В отличие от вавилонской системы, греческое основание 60 не использовалось для выражения целых чисел.
В этой шестидесятеричной позиционной системе с подбазой 10 для выражения дробей использовались четырнадцать буквенных цифр (единицы от 1 до 9 и декады от 10 до 50) для записи любого числа от 1 до 59. Они могли быть числителем дроби. Позиционный принцип использовался для знаменателя дроби, которая записывалась с показателем степени 60 (60, 3600, 216000 и т. д.). Шестидесятеричные дроби могли использоваться для выражения любого дробного значения, при этом последовательные позиции представляли 1/60, 1/60 2 , 1/60 3 и т. д. [14] Первым крупным текстом, в котором появилась эта смешанная система, был Альмагест Птолемея , написанный во 2 веке нашей эры. [15]
Астрономические дроби (со знаками греческого алфавита):
Эта смешанная система не использовала точку основания , но астрономические дроби имели специальный знак для обозначения нуля в качестве заполнителя. Некоторые поздние вавилонские тексты использовали похожий заполнитель. Греки переняли эту технику, используя свой собственный знак, форма и характер которого со временем изменились от ранних рукописей (I век н.э.) до алфавитной записи. [16]
Эта шестидесятеричная система обозначений была особенно полезна в астрономии и математике из-за деления окружности на 360 градусов (с подразделениями 60 минут на градус и 60 секунд на минуту). В комментарии Теона Александрийского (IV в. н. э.) к Альмагесту числовая фраза ͵αφιε κ ιε выражает 1515 ( ͵αφιε ) градусов, 20 ( κ ) минут и 15 ( ιε ) секунд. [17] Значение градуса указывается в обычных десятичных алфавитных цифрах, включая использование мультипликативной хасты для 1000, в то время как последние две позиции записываются в шестидесятеричных дробях.
Арабы переняли астрономические дроби непосредственно у греков, а еврейские астрономы использовали шестидесятеричные дроби, но греческие числовые знаки были заменены их собственными буквенными числовыми знаками для выражения как целых чисел, так и дробей.