Инъективный объект

В математике , особенно в области теории категорий , понятие инъективного объекта является обобщением понятия инъективного модуля . Это понятие важно в когомологиях , в теории гомотопий и в теории модельных категорий . Двойственное понятие — это понятие проективного объекта .

Определение

Объект `Q` является инъективным, если для данного мономорфизма `f` : `X` → `Y` любой `g` : `X` → `Q` можно расширить до `Y` .

Объект в категории называется инъективным, если для каждого мономорфизма и каждого морфизма существует морфизм, продолжающийся до , т . е. такой, что . ^[1] $Q$ $\mathbf {C}$ $f:X\to Y$ $g:X\to Q$ $h:Y\to Q$ $г$ $Y$ ${\ displaystyle h \ circ f = g}$

То есть каждый морфизм проходит через каждый мономорфизм . $X\to Q$ $X\hookrightarrow Y$

Морфизм в приведенном выше определении не обязательно должен однозначно определяться и . $ч$ $е$ $г$

В локально малой категории это эквивалентно требованию, чтобы функтор hom переносил мономорфизмы в сюръективные отображения множеств. $\operatorname {Hom} _ {\mathbf {C} }(-,Q)$ $\mathbf {C}$

В абелевых категориях

Понятие инъективности было впервые сформулировано для абелевых категорий , и это до сих пор является одной из основных областей его применения. Когда категория Q является абелевой, объект Q инъективен тогда и только тогда, когда его hom -функтор Hom _C (–, Q ) точен . $\mathbf {C}$ $\mathbf {C}$

Если - точная последовательность в такой, что Q инъективен, то последовательность расщепляется . $0\к Q\к U\к V\к 0$ $\mathbf {C}$

Достаточно инъективных и инъективных оболочек

Говорят, что категория имеет достаточно инъективных элементов , если для каждого объекта X из существует мономорфизм X в инъективный объект. $\mathbf {C}$ $\mathbf {C}$

Мономорфизм g называется существенным мономорфизмом , если для любого морфизма f композиция fg является мономорфизмом только в том случае, если f является мономорфизмом. $\mathbf {C}$

Если g — существенный мономорфизм с областью X и инъективной кообластью G , то G называется инъективной оболочкой X. Тогда инъективная оболочка определяется X однозначно с точностью до неканонического изоморфизма. ^[1]

Примеры

В категории абелевых групп и групповых гомоморфизмов Ab инъективный объект обязательно является делимой группой . Если принять аксиому выбора, то понятия эквивалентны.
В категории (левых) модулей и гомоморфизмов модулей R — Mod инъективный объект является инъективным модулем . R - Mod имеет инъективные оболочки (как следствие, R - Mod имеет достаточно инъективных форм).
В категории метрических пространств Met инъективный объект — это инъективное метрическое пространство , а инъективная оболочка метрического пространства — это его узкая оболочка .
В категории пространств T0 и непрерывных отображений инъективный объект всегда является топологией Скотта на непрерывной решетке и, следовательно, всегда трезв и локально _{компактен} .

Использование

Если в абелевой категории достаточно инъектив, мы можем формировать инъективные резольвенты , т. е. для данного объекта X мы можем сформировать длинную точную последовательность

0\to X\to Q^{0}\to Q^{1}\to Q^{2}\to \cdots

и затем можно определить производные функторы данного функтора F , применив F к этой последовательности и вычислив гомологии полученной (не обязательно точной) последовательности. Этот подход используется для определения функторов Ext и Tor , а также различных теорий когомологий в теории групп , алгебраической топологии и алгебраической геометрии . Используемые категории обычно представляют собой категории функторов или категории пучков модулей O _X в некотором кольцевом пространстве ( X , O _X ) или, в более общем смысле, любую категорию Гротендика .

Обобщение

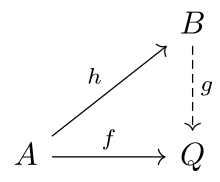
Пусть – категория и пусть – класс морфизмов . $\mathbf {C}$ ${\mathcal {H}}$ $\mathbf {C}$

Объект называется -инъективным, если для каждого морфизма и каждого морфизма в существует морфизм с . $Q$ $\mathbf {C}$ ${\mathcal {H}}$ $f:A\to Q$ ${\ displaystyle h: A \ to B}$ ${\mathcal {H}}$ $g:B\to Q$ ${\ displaystyle g \ circ h = f}$

Если – класс мономорфизмов , мы возвращаемся к инъективным объектам, рассмотренным выше. ${\mathcal {H}}$

Говорят, что категория имеет достаточное количество -инъективных объектов , если для каждого объекта X из существует -морфизм из X в -инъективный объект. $\mathbf {C}$ ${\mathcal {H}}$ $\mathbf {C}$ ${\mathcal {H}}$ ${\mathcal {H}}$

-Морфизм g in называется -существенным , если для любого морфизма f составной fg находится в только в том случае, если f находится в . ${\mathcal {H}}$ $\mathbf {C}$ ${\mathcal {H}}$ ${\mathcal {H}}$ ${\mathcal {H}}$

Если g — -существенный морфизм с областью определения X и -инъективной кообластью G , то G называется -инъективной оболочкой X. ^[1] ${\mathcal {H}}$ ${\mathcal {H}}$ ${\mathcal {H}}$

Примеры H -инъективных объектов

В категории симплициальных множеств инъективными объектами по отношению к классу анодинных расширений являются кановские комплексы . ${\mathcal {H}}$
В категории частично упорядоченных множеств и монотонных отображений полные решетки образуют инъективные объекты для класса порядковых вложений , а пополнение Дедекинда – МакНила частично упорядоченного множества является его -инъективной оболочкой. ${\mathcal {H}}$ ${\mathcal {H}}$

Смотрите также

Проективный объект

Примечания

^ abc Адамек, Иржи; Херрлих, Хорст; Стрекер, Джордж (1990). «Раздел 9. Инъективные объекты и существенные вложения». Абстрактные и конкретные категории: Кошачья радость (PDF) . Перепечатки по теории и приложениям категорий, № 17 (2006), стр. 1–507. ориг. Джон Уайли. стр. 147–155.