Закон косинусов

Свойство всех треугольников на евклидовой плоскости

Рис. 1 – Треугольник. Углы α (или A ), β (или B ) и γ (или C ) противолежат сторонам a , b и c соответственно .

В тригонометрии закон косинусов (также известный как формула косинусов или правило косинусов ) связывает длины сторон треугольника с косинусом одного из его углов . Для треугольника со сторонами и противоположными соответствующими углами и (см. рис. 1) закон косинусов гласит: ${\displaystyle a,}$ ${\displaystyle b,}$ ${\displaystyle c,}$ ${\displaystyle \alpha ,}$ ${\displaystyle \beta ,}$ ${\displaystyle \gamma }$

${\displaystyle {\begin{aligned}c^{2}&=a^{2}+b^{2}-2ab\cos \gamma ,\\[3mu]a^{2}&=b^{2}+c^{2}-2bc\cos \alpha ,\\[3mu]b^{2}&=a^{2}+c^{2}-2ac\cos \beta .\end{aligned}}}$

Закон косинусов обобщает теорему Пифагора , справедливую только для прямоугольных треугольников : если угол прямой, то и закон косинусов сводится к ${\displaystyle \gamma }$ ${\displaystyle \cos \gamma =0,}$ ${\displaystyle c^{2}=a^{2}+b^{2}.}$

Закон косинусов полезен для решения треугольника , когда заданы все три или две стороны и прилежащий к ним угол.

Использование при решении треугольников.

Рис. 3 – Применение закона косинусов: неизвестная сторона и неизвестный угол.

Учитывая стороны треугольника b и c и угол γ, иногда есть два решения для a .

Теорема используется при решении треугольников , т.е. для нахождения (см. рисунок 3):

• третья сторона треугольника, если известны две стороны и угол между ними:
  $${\displaystyle c={\sqrt {a^{2}+b^{2}-2ab\cos \gamma }}\,;}$$
• углы треугольника, если известны три стороны:
  $${\displaystyle \gamma =\arccos \left({\frac {a^{2}+b^{2}-c^{2}}{2ab}}\right)\,;}$$
• третья сторона треугольника, если известны две стороны и угол, противоположный одной из них (эту сторону также можно найти двумя применениями закона синусов ): ^[1]

$${\displaystyle a=b\cos \gamma \pm {\sqrt {c^{2}-b^{2}\sin ^{2}\gamma }}\,.}$$

Эти формулы дают большие ошибки округления при вычислениях с плавающей запятой , если треугольник очень острый, т. е. если c мало по отношению к a , а b или γ мало по сравнению с 1. Можно даже получить результат, немного превышающий единицу. для косинуса угла.

Третья показанная формула является результатом решения квадратного уравнения a ² − 2 ab cos γ + b ² − c ² = 0 . Это уравнение может иметь 2, 1 или 0 положительных решений, что соответствует количеству возможных треугольников с учетом данных. Оно будет иметь два положительных решения, если b sin γ < c < b , только одно положительное решение, если c = b sin γ , и не иметь решения, если c < b sin γ . Эти разные случаи также объясняются неоднозначностью сравнения сторон и углов .

История

Книга II « Начал» Евклида , составленная ок. 300 г. до н.э., основанный на материале, написанном на столетие или два старше, содержит геометрическую теорему, соответствующую закону косинусов, но выраженную на современном языке площадей прямоугольников; Эллинистическая тригонометрия возникла позже, а синус и косинус сами по себе впервые появились столетия спустя в Индии.

Случаи тупоугольных и остроугольных треугольников (соответствующие двум случаям отрицательного или положительного косинуса) рассматриваются отдельно в предложениях II.12 и II.13: ^[2]

Предложение 12.
В тупоугольных треугольниках квадрат на стороне, стягивающей тупой угол, больше квадратов на сторонах, содержащих тупой угол, в два раза больше прямоугольника, содержащегося на одной из сторон вокруг тупого угла, а именно на том, на котором перпендикуляр падает, и прямая отсекается снаружи перпендикуляром к тупому углу.

-  Элементы Евклида , перевод Томаса Л. Хита . ^[2]

Предложение 13 содержит аналогичное утверждение для остроугольных треугольников. В своем комментарии (ныне утерянном и сохранившемся лишь в виде фрагментарных цитат) Герон Александрийский представил доказательства обратного как в II.12, так и в II.13. ^[3]

Рис. 2 – Тупоугольный треугольник ABC с перпендикуляром BH

Используя обозначения, показанные на рис. 2, формулировку предложения II.12 Евклида можно представить более кратко (хотя и анахронично) формулой

${\displaystyle AB^{2}=CA^{2}+CB^{2}+2(CA)(CH).}$

Чтобы преобразовать это в знакомое выражение закона косинусов, замените и ${\displaystyle AB=c,}$ ${\displaystyle CA=b,}$ ${\displaystyle CB=a,}$ ${\displaystyle CH=a\cos(\pi -\gamma )\ }$ ${\displaystyle =-a\cos \gamma .}$

Предложение II.13 не использовалось во времена Евклида для решения треугольников, но позже оно использовалось таким образом при решении астрономических задач аль -Бируни (11 век) и Иоганнесом де Мюрисом (14 век). ^[4] Нечто, эквивалентное сферическому закону косинусов , использовалось (но не было сформулировано в целом) аль-Хорезми (9 век), аль-Баттани (9 век) и Нилакантой (15 век). ^[5]

Джамшид аль-Каши , персидский математик и астроном XV века, вычисливший самые точные тригонометрические таблицы своего времени, писал о решении треугольников в своем «Мифтах аль-Хисаб» ( «Ключ арифметики» , 1427 г.), включая следующий метод нахождения третья сторона с учетом двух сторон и прилежащего к ним угла: ^[6]

Версия закона косинусов Аль-Каши (случай, когда γ тупой), выраженная в современных алгебраических обозначениях.

Другой случай , когда известны две стороны и угол между ними, а остальные неизвестны. Мы умножаем одну из сторон на синус [известного] угла один раз и на синус его дополнения, другой раз преобразуем, и вычитаем второй результат из другой стороны, если угол острый, и прибавляем его, если угол равен тупой. Затем мы возводим результат в квадрат и добавляем к нему квадрат первого результата. Извлекаем квадратный корень из суммы, чтобы получить оставшуюся часть....

-  Мифтах аль-Хисаб Аль- Каши ,
     перевод Нуха Айдина, Лахдара Хаммуди и Гады Бакбука ^[7]

Используя современные алгебраические обозначения и соглашения, это можно было бы записать

${\displaystyle c={\sqrt {(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}}}}$

когда острый или ${\displaystyle \gamma }$

${\displaystyle c={\sqrt {\left(b+a\left|\cos \gamma \right|\right)^{2}+\left(a\sin \gamma \right)^{2}}}}$

когда тупо (когда тупо, современное соглашение таково, что оно отрицательное и положительное; исторически синусы и косинусы считались отрезками прямой с неотрицательной длиной). Возведя обе части в квадрат, разложив квадрат бинома и затем применив тригонометрическое тождество Пифагора, мы получаем знакомый закон косинусов: ${\displaystyle \gamma }$ ${\displaystyle \gamma }$ ${\displaystyle \cos \gamma }$ ${\displaystyle \cos(\pi -\gamma )=-\cos \gamma }$ ${\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1,}$

${\displaystyle {\begin{aligned}c^{2}&=b^{2}-2ba\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\[5mu]&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}}$

Во Франции закон косинусов иногда называют теоремой д'Аль-Каши . ^{[8] [9]}

Метод Аль-Каши, по сути, аналогичен методу, рекомендованному для решения таких треугольников в книге Насира ад-Дина ат-Туси « Китаб аль-Шакл аль-катта» ( «Книга о полном четырехугольнике» , ок. 1250 г.), но с описанными шагами. явно, вместо того, чтобы оставлять детали читателю. ^[10]

Теорема была впервые записана с использованием алгебраических обозначений Франсуа Вьета в 16 веке. В начале XIX века современные алгебраические обозначения позволили записать закон косинусов в его нынешней символической форме. ^[11]

Доказательства

Используя теорему Пифагора

Доказательство закона косинусов в остроугольных и тупоугольных треугольниках с помощью теоремы Пифагора.

Тупоугольный треугольник ABC с высотой BH.

Случай тупого угла

Евклид доказал эту теорему, применив теорему Пифагора к каждому из двух прямоугольных треугольников на рис. 2 ( AHB и CHB ). Используя d для обозначения отрезка CH и h для высоты BH , треугольник AHB дает нам

${\displaystyle c^{2}=(b+d)^{2}+h^{2},}$

и треугольник CHB дает

${\displaystyle d^{2}+h^{2}=a^{2}.}$

Разложение первого уравнения дает

${\displaystyle c^{2}=b^{2}+2bd+d^{2}+h^{2}.}$

Подставив в это второе уравнение, можно получить следующее:

${\displaystyle c^{2}=a^{2}+b^{2}+2bd.}$

Это 12-е предложение Евклида из второй книги « Начал» . ^[12] Чтобы преобразовать его в современную форму закона косинусов, заметим, что

${\displaystyle d=a\cos(\pi -\gamma )=-a\cos \gamma .}$

Случай острого угла

Доказательство Евклидом его предложения 13 идет по той же схеме, что и его доказательство предложения 12: он применяет теорему Пифагора к обоим прямоугольным треугольникам, образованным путем опускания перпендикуляра на одну из сторон, охватывающих угол γ, и использует квадрат разности для упрощения .

Еще одно доказательство в остром случае

Рис. 6 – Краткое доказательство с использованием тригонометрии для случая острого угла

Используя больше тригонометрии, закон косинусов можно вывести, применив теорему Пифагора только один раз. Фактически, используя прямоугольный треугольник в левой части рис. 6, можно показать, что:

${\displaystyle {\begin{aligned}c^{2}&=(b-a\cos \gamma )^{2}+(a\sin \gamma )^{2}\\&=b^{2}-2ab\cos \gamma +a^{2}\cos ^{2}\gamma +a^{2}\sin ^{2}\gamma \\&=b^{2}+a^{2}-2ab\cos \gamma ,\end{aligned}}}$

используя тригонометрическое тождество ${\displaystyle \cos ^{2}\gamma +\sin ^{2}\gamma =1.}$

Это доказательство нуждается в небольшой модификации, если b < a cos( γ ) . В этом случае прямоугольный треугольник, к которому применяется теорема Пифагора, выходит за пределы треугольника ABC . Единственное влияние, которое это оказывает на расчет, заключается в том, что величина b − a cos( γ ) заменяется на a cos( γ ) − b . Поскольку эта величина входит в расчет только через свой квадрат, остальная часть доказательства не затрагивается. Однако эта проблема возникает только тогда, когда β тупой, и ее можно избежать, отразив треугольник вокруг биссектрисы γ .

Ссылаясь на рис. 6, стоит отметить, что если угол, противоположный стороне a, равен α , то:

${\displaystyle \tan \alpha ={\frac {a\sin \gamma }{b-a\cos \gamma }}.}$

Это полезно для прямого расчета второго угла, когда заданы две стороны и прилежащий угол.

С трёх высот

Рис. 5 – Остроугольный треугольник с перпендикуляром

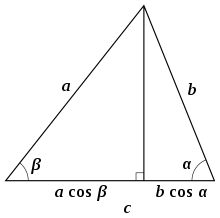
Высота , проходящая через вершину C, представляет собой отрезок, перпендикулярный стороне c . Расстояние от подножия высоты до вершины А плюс расстояние от подножия высоты до вершины В равно длине стороны с (см. рис. 5). Каждое из этих расстояний можно записать как произведение одной из других сторон на косинус прилежащего угла: ^[13]

${\displaystyle c=a\cos \beta +b\cos \alpha .}$

(Это по-прежнему верно, если α или β тупые, и в этом случае перпендикуляр выходит за пределы треугольника.) Умножение обеих сторон на c дает

${\displaystyle c^{2}=ac\cos \beta +bc\cos \alpha .}$

Те же шаги работают так же хорошо, если рассматривать любую из других сторон как основание треугольника:

${\displaystyle {\begin{aligned}a^{2}&=ac\cos \beta +ab\cos \gamma ,\\[3mu]b^{2}&=bc\cos \alpha +ab\cos \gamma .\end{aligned}}}$

Взяв уравнение для и вычитая уравнения для и ${\displaystyle c^{2}}$ ${\displaystyle b^{2}}$ ${\displaystyle a^{2},}$

${\displaystyle {\begin{aligned}c^{2}-a^{2}-b^{2}&={\color {BlueGreen}{\cancel {\color {Black}ac\cos \beta }}}+{\color {Peach}{\cancel {\color {Black}bc\cos \alpha }}}-{\color {BlueGreen}{\cancel {\color {Black}ac\cos \beta }}}-{\color {Peach}{\cancel {\color {Black}bc\cos \alpha }}}-2ab\cos \gamma \\c^{2}&=a^{2}+b^{2}-2ab\cos \gamma .\end{aligned}}}$

Это доказательство не зависит от теоремы Пифагора , поскольку оно основано только на определении косинуса в прямоугольном треугольнике и алгебраически получает квадраты длин сторон. Другие доказательства обычно явно ссылаются на теорему Пифагора и являются более геометрическими, рассматривая cos  γ как метку длины определенного отрезка прямой. ^[13]

В отличие от многих доказательств, в этом унифицировано рассматриваются случаи тупых и острых углов γ .

Декартовы координаты

Рис. 4 – Доказательство координатной геометрии

Рассмотрим треугольник со сторонами длиной a , b , c , где θ — это угол, противоположный стороне длины c . Этот треугольник можно поместить в декартову систему координат со стороной a , выровненной по оси x , и углом θ , расположенным в начале координат, путем нанесения на график компонентов трех точек треугольника, как показано на рис. 4:

${\displaystyle A=(b\cos \theta ,b\sin \theta ),B=(a,0),{\text{ and }}C=(0,0).}$

По формуле расстояния ,

${\displaystyle c={\sqrt {(a-b\cos \theta )^{2}+(0-b\sin \theta )^{2}}}.}$

Возведение в квадрат обеих сторон и упрощение

${\displaystyle {\begin{aligned}c^{2}&=(a-b\cos \theta )^{2}+(-b\sin \theta )^{2}\\&=a^{2}-2ab\cos \theta +b^{2}\cos ^{2}\theta +b^{2}\sin ^{2}\theta \\&=a^{2}+b^{2}(\sin ^{2}\theta +\cos ^{2}\theta )-2ab\cos \theta \\&=a^{2}+b^{2}-2ab\cos \theta .\end{aligned}}}$

Преимущество этого доказательства в том, что оно не требует рассмотрения различных случаев, когда треугольник остроугольный, прямоугольный или тупоугольный.

Используя теорему Птолемея

Доказательство закона косинусов с помощью теоремы Птолемея.

На схеме треугольник ABC со сторонами AB = c , BC = a и AC = b нарисован внутри описанной окружности, как показано. Треугольник ABD построен равным треугольнику ABC , причем AD = BC и BD = AC . Перпендикуляры из D и C пересекают основание AB в точках E и F соответственно. Затем:

${\displaystyle {\begin{aligned}&BF=AE=BC\cos {\hat {B}}=a\cos {\hat {B}}\\\Rightarrow \ &DC=EF=AB-2BF=c-2a\cos {\hat {B}}.\end{aligned}}}$

Теперь закон косинусов выражается прямым применением теоремы Птолемея к вписанному четырехугольнику ABCD :

${\displaystyle {\begin{aligned}&AD\times BC+AB\times DC=AC\times BD\\\Rightarrow \ &a^{2}+c(c-2a\cos {\hat {B}})=b^{2}\\\Rightarrow \ &a^{2}+c^{2}-2ac\cos {\hat {B}}=b^{2}.\end{aligned}}}$

Очевидно, что если угол B прямой , то ABCD — прямоугольник, и применение теоремы Птолемея приводит к теореме Пифагора :

${\displaystyle a^{2}+c^{2}=b^{2}.\quad }$

Сравнивая области

Рис. 7а – Доказательство закона косинусов для острого угла γ методом «вырезания и склеивания».

Рис. 7б – Доказательство закона косинусов для тупого угла γ методом «вырезания и склеивания».

Закон косинусов можно также доказать, вычислив площади . Изменение знака по мере того, как угол γ становится тупым, делает необходимым различие падежей.

Напомним, что

• a ² , b ² и c ² — площади квадратов со сторонами a , b и c соответственно;
• если γ острый, то ab cos γ — площадь параллелограмма со сторонами a и b , образующими угол γ′ =π/2− γ ;
• если γ тупой, и поэтому cos γ отрицательен, то − ab cos γ — это площадь параллелограмма , стороны a и b которого образуют угол γ′ = γ −π/2.

Острый случай. На рис. 7а показан семиугольник , разрезанный на более мелкие части (двумя разными способами), что дает доказательство закона косинусов. Различные части

• розовым цветом обозначены области a ² , b ² слева и области 2 ab cos γ и c ² справа;
• синим цветом треугольник ABC слева и справа;
• серым цветом — вспомогательные треугольники, все конгруэнтные ABC , одинаковое число (а именно 2) как слева, так и справа .

Равенство площадей слева и справа дает

${\displaystyle \,a^{2}+b^{2}=c^{2}+2ab\cos \gamma \,.}$

Тупой случай. На рисунке 7б шестиугольник разрезается на более мелкие части двумя разными способами, что дает доказательство закона косинусов в случае, когда угол γ тупой. У нас есть

• розовым цветом обозначены области a ² , b ² и -2 ab cos γ слева и c ² справа;
• синим цветом треугольник ABC дважды, слева и справа.

Равенство площадей слева и справа дает

${\displaystyle \,a^{2}+b^{2}-2ab\cos(\gamma )=c^{2}.}$

Строгое доказательство должно будет включать доказательства того, что различные фигуры конгруэнтны и, следовательно, имеют одинаковую площадь. Для этого воспользуемся теорией равных треугольников .

Использование геометрии круга

Рис. 8а – Треугольник ABC (розовый), вспомогательный круг (голубой) и вспомогательный прямоугольный треугольник (желтый)

Рис. 8б – Треугольник ABC (розовый), вспомогательный круг (голубой) и два вспомогательных прямоугольных треугольника (желтый)

Рис. 9 – Доказательство закона косинусов с использованием силы точечной теоремы.

Используя геометрию круга , можно дать более геометрическое доказательство, чем используя одну лишь теорему Пифагора . Алгебраические манипуляции (в частности, биномиальная теорема ) избегаются.

Случай острого угла γ , где a > 2 b cos γ . Опустите перпендикуляр из A на a = BC , создав отрезок длиной b cos γ . Дублируйте прямоугольный треугольник , чтобы сформировать равнобедренный треугольник ACP . Постройте круг с центром A и радиусом b и его касательной h = BH , проходящей через B. Касательная h образует прямой угол с радиусом b ( Начала Евклида : Книга 3, Предложение 18; или см. здесь ), поэтому желтый треугольник на рисунке 8 является прямым. Примените теорему Пифагора , чтобы получить

${\displaystyle c^{2}=b^{2}+h^{2}.}$

Затем используйте теорему о касательном секущем ( Начала Евклида : Книга 3, Предложение 36), которая гласит, что квадрат касательной, проходящей через точку B вне круга, равен произведению двух отрезков прямой (из B ), созданных любым секущим . круга через B. В данном случае: BH ² = BC · BP , или

${\displaystyle h^{2}=a(a-2b\cos \gamma ).}$

Подстановка в предыдущее уравнение дает закон косинусов:

${\displaystyle c^{2}=b^{2}+a(a-2b\cos \gamma ).}$

Обратите внимание, что h ² — это степень точки B относительно окружности. Использование теоремы Пифагора и теоремы о касательном секущем можно заменить однократным применением теоремы о мощности точки .

Случай острого угла γ , где a < 2 b cos γ . Опустите перпендикуляр из A на a = BC , создав отрезок длиной b cos γ . Дублируйте прямоугольный треугольник , чтобы сформировать равнобедренный треугольник ACP . Постройте круг с центром A и радиусом b , а также хордой , проходящей через B , перпендикулярной c = AB , половина которой равна h = BH . Примените теорему Пифагора , чтобы получить

${\displaystyle b^{2}=c^{2}+h^{2}.}$

Теперь используйте теорему о хорде ( Начала Евклида : Книга 3, Предложение 35), которая гласит, что если две хорды пересекаются, произведение двух отрезков, полученных на одной хорде, равно произведению двух отрезков, полученных на другой хорде. . В данном случае: BH ² = BC · BP , или

${\displaystyle h^{2}=a(2b\cos \gamma -a).}$

Подстановка в предыдущее уравнение дает закон косинусов:

${\displaystyle b^{2}=c^{2}+a(2b\cos \gamma -a)\,.}$

Обратите внимание, что степень точки B относительно окружности имеет отрицательное значение − h ² .

Случай тупого угла γ . В этом доказательстве напрямую используется сила точечной теоремы, без вспомогательных треугольников, полученных путем построения касательной или хорды. Постройте круг с центром B и радиусом a (см . рисунок 9), который пересекает секущие через A и C в C и K. Степень точки A относительно окружности равна как AB ² − BC ² , так и AC · AK . Поэтому,

${\displaystyle {\begin{aligned}c^{2}-a^{2}&{}=b(b+2a\cos(\pi -\gamma ))\\&{}=b(b-2a\cos \gamma ),\end{aligned}}}$

что является законом косинусов.

Используя алгебраические меры для отрезков линий (допуская отрицательные числа в качестве длин отрезков), случай тупого угла ( CK > 0 ) и острого угла ( CK < 0 ) можно рассматривать одновременно.

Используя закон синусов

Используя закон синусов и зная, что сумма углов треугольника должна составлять 180 градусов, мы имеем следующую систему уравнений (три неизвестных — это углы):

${\displaystyle {\frac {c}{\sin \gamma }}={\frac {b}{\sin \beta }},}$

${\displaystyle {\frac {c}{\sin \gamma }}={\frac {a}{\sin \alpha }},}$

${\displaystyle \alpha +\beta +\gamma =\pi .}$

Тогда, воспользовавшись третьим уравнением системы, получим систему двух уравнений с двумя переменными:

${\displaystyle {\frac {c}{\sin \gamma }}={\frac {b}{\sin(\alpha +\gamma )}},}$

${\displaystyle {\frac {c}{\sin \gamma }}={\frac {a}{\sin \alpha }},}$

где мы использовали тригонометрическое свойство, заключающееся в том, что синус дополнительного угла равен синусу угла.

Использование тождества (см. Тождества суммы углов и разностей )

${\displaystyle \sin(\alpha +\gamma )=\sin \alpha \cos \gamma +\sin \gamma \cos \alpha }$

приводит к

${\displaystyle c(\sin \alpha \cos \gamma +\sin \gamma \cos \alpha )=b\sin \gamma ,}$

${\displaystyle c\sin \alpha =a\sin \gamma .}$

Разделив всю систему на cos γ , мы получим:

${\displaystyle c(\sin \alpha +\tan \gamma \cos \alpha )=b\tan \gamma ,}$

${\displaystyle {\frac {c\sin \alpha }{\cos \gamma }}=a\tan \gamma ,}$

${\displaystyle {\frac {c^{2}\sin ^{2}\alpha }{\cos ^{2}\gamma }}=a^{2}\tan ^{2}\gamma .}$

Следовательно, из первого уравнения системы можно получить

${\displaystyle {\frac {c\sin \alpha }{b-c\cos \alpha }}=\tan \gamma }$

Подставив это выражение во второе уравнение и воспользовавшись

${\displaystyle 1+\tan ^{2}\gamma ={\frac {1}{\cos ^{2}\gamma }}}$

мы можем получить одно уравнение с одной переменной:

${\displaystyle c^{2}\sin ^{2}\alpha \left[1+{\frac {c^{2}\sin ^{2}\alpha }{(b-c\cos \alpha )^{2}}}\right]=a^{2}\cdot {\frac {c^{2}\sin ^{2}\alpha }{(b-c\cos \alpha )^{2}}}}$

Умножив на ( b − c cos α ) ² , мы можем получить следующее уравнение:

${\displaystyle (b-c\cos \alpha )^{2}+c^{2}\sin ^{2}\alpha =a^{2}.}$

Из этого следует

${\displaystyle b^{2}-2bc\cos \alpha +c^{2}\cos ^{2}\alpha +c^{2}\sin ^{2}\alpha =a^{2}.}$

Вспоминая тождество Пифагора , получаем закон косинусов:

${\displaystyle a^{2}=b^{2}+c^{2}-2bc\cos \alpha .}$

Использование векторов

Обозначим

${\displaystyle {\overrightarrow {CB}}={\vec {a}},\ {\overrightarrow {CA}}={\vec {b}},\ {\overrightarrow {AB}}={\vec {c}}}$

Поэтому,

${\displaystyle {\vec {c}}={\vec {a}}-{\vec {b}}}$

Взяв скалярное произведение каждой стороны с собой:

${\displaystyle {\vec {c}}\cdot {\vec {c}}=({\vec {a}}-{\vec {b}})\cdot ({\vec {a}}-{\vec {b}})}$

${\displaystyle \Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+\Vert {\vec {b}}\Vert ^{2}-2\,{\vec {a}}\cdot {\vec {b}}}$

Использование личности

${\displaystyle {\vec {u}}\cdot {\vec {v}}=\Vert {\vec {u}}\Vert \,\Vert {\vec {v}}\Vert \cos \angle ({\vec {u}},\ {\vec {v}})}$

приводит к

${\displaystyle \Vert {\vec {c}}\Vert ^{2}=\Vert {\vec {a}}\Vert ^{2}+{\Vert {\vec {b}}\Vert }^{2}-2\,\Vert {\vec {a}}\Vert \!\;\Vert {\vec {b}}\Vert \cos \angle ({\vec {a}},\ {\vec {b}})}$

Результат следующий.

Равнобедренный случай

Когда a = b , т. е. когда треугольник равнобедренный , причем две стороны, лежащие на угле γ , равны, закон косинусов существенно упрощается. А именно, поскольку a ² + b ² = 2 a ² = 2 ab , закон косинусов принимает вид

${\displaystyle \cos \gamma =1-{\frac {c^{2}}{2a^{2}}}}$

или

${\displaystyle c^{2}=2a^{2}(1-\cos \gamma ).}$

Аналог тетраэдров

Аналогичное утверждение начинается с того, что α , β , γ , δ считаются площадями четырех граней тетраэдра . Обозначим двугранные углы через и т. д. Тогда ^[14] ${\displaystyle {\widehat {\beta \gamma }}}$

${\displaystyle \alpha ^{2}=\beta ^{2}+\gamma ^{2}+\delta ^{2}-2\left[\beta \gamma \cos \left({\widehat {\beta \gamma }}\right)+\gamma \delta \cos \left({\widehat {\gamma \delta }}\right)+\delta \beta \cos \left({\widehat {\delta \beta }}\right)\right].}$

Версия подходит для небольших углов

Когда угол γ мал, а прилегающие стороны a и b имеют одинаковую длину, правая часть стандартной формы закона косинусов подвергается катастрофическому сокращению в числовых приближениях. В ситуациях, когда это важно, может оказаться полезной математически эквивалентная версия закона косинусов, подобная формуле хаверсинуса :

${\displaystyle {\begin{aligned}c^{2}&=(a-b)^{2}+4ab\sin ^{2}\left({\frac {\gamma }{2}}\right)\\&=(a-b)^{2}+4ab\operatorname {haversin} (\gamma ).\end{aligned}}}$

В пределе бесконечно малого угла закон косинусов вырождается в формулу длины дуги окружности c = a γ .

В сферической и гиперболической геометрии

Сферический треугольник решается по закону косинусов.

Версии, аналогичные закону косинусов для евклидовой плоскости, справедливы и на единичной сфере и в гиперболической плоскости. В сферической геометрии треугольник определяется тремя точками u , v и w на единичной сфере и дугами больших кругов , соединяющими эти точки. Если эти большие круги образуют углы A , B и C с противоположными сторонами a , b , c, то сферический закон косинусов утверждает, что выполняются оба следующих соотношения:

${\displaystyle {\begin{aligned}\cos a&=\cos b\cos c+\sin b\sin c\cos A\\\cos A&=-\cos B\cos C+\sin B\sin C\cos a.\end{aligned}}}$

В гиперболической геометрии пара уравнений известна под общим названием гиперболический закон косинусов . Первое - это

${\displaystyle \cosh a=\cosh b\cosh c-\sinh b\sinh c\cos A}$

где sinh и cosh — гиперболические синус и косинус , а второй —

${\displaystyle \cos A=-\cos B\cos C+\sin B\sin C\cosh a.}$

Как и в евклидовой геометрии, можно использовать закон косинусов для определения углов A , B , C по знанию сторон a , b , c . В отличие от евклидовой геометрии, в обеих неевклидовых моделях возможен и обратный процесс: углы A , B , C определяют стороны a , b , c .

Смотрите также

• Полусторонняя формула
• Закон синусов
• Закон касательных
• Закон котангенсов
• Список тригонометрических тождеств
• Формула Молвейде

Рекомендации

1. Указанные стороны и угол можно найти с помощью закона синусов, оставляя до двух вариантов угла . Любой выбор имеет решающее значение , поскольку сумма трех внутренних углов образует прямой угол. Наконец, можно найти другое применение закона синусов. ${\displaystyle b,c}$ ${\displaystyle \gamma ,}$ ${\displaystyle \sin \beta }$ ${\displaystyle \beta }$ ${\displaystyle \alpha }$ ${\displaystyle a}$ ${\displaystyle c,\gamma ,\alpha }$
2. Евклид. Томас Л. Хит (ред.). «Элементы». Перевод Томаса Л. Хита . Проверено 24 января 2023 г.
3. Хит, Томас (1956) [1908]. "Введение" . Тринадцать книг элементов Евклида (2-е изд.).
4. Кеннеди, ES; Мурувва, Ахмад (1958). «Бируни о солнечном уравнении». Журнал ближневосточных исследований . 17 (2): 112–121. JSTOR  542617.
   Йоханнес де Мюрис благодарит анонимного автора за соответствующий раздел своей работы De Arte Mesurandi . См. Ван Браммелен, Глен (2009). Математика неба и земли . Издательство Принстонского университета. стр. 240–241.
5. Ван Браммелен, Глен (2012). Небесная математика: Забытое искусство сферической тригонометрии . Издательство Принстонского университета. п. 98.
6. Азарян, Мохаммад К. (2000). «Мефтаб Аль-Хесаб: Краткое содержание». Миссурийский журнал математических наук . 12 (2): 75–95. дои : 10.35834/2000/1202075 .
7. Айдын, Нух; Хаммуди, Лахдар; Бакбук, Гада (2020). «Мифтах аль-Хисаб» Аль-Каши, Том II: Геометрия . Биркхойзер. п. 31. дои : 10.1007/978-3-030-61330-3.
8. Пиковер, Клиффорд А. (2009). Книга по математике: от Пифагора до 57-го измерения. Стерлинг Паблишинг Компани, Инк. 106. ИСБН 9781402757969.
9. Программа математики de première générale (на французском языке). Министерство национального образования и молодежи. 2022. С. 11, 12.
10. Нашир ад-Дин аль-Туси (1891). «Гл. 3.2: Sur la manière de Calculer les Côtés et les angulars d'un треугольника les uns par les autres». Traité du Quadrilatère, приписываемый Насируддинелю-Тусси (на французском языке). Перевод Каратеодори, Александр Паша . Типография и литография Османие. п. 69. На двух котах и ​​под углом. [...] Que si l'angle donné est состоит из двух частей AB AC, abaissez de B sur AC la perpendiculaire BE. Vous aurez ainsi le треугольник прямоугольник [BEA] не знает границ le Côté AB и l'angle A; он снова BE, EA и т. д. снова в предыдущих случаях; в. à. д. в этом случае BE, CE sont connus; on connaîtra dès lors BC et l'angle C, comme nous l'avons expliqué [Учитывая [...], что угол A заключен между двумя сторонами AB AC, опустите от B до AC перпендикуляр BE. Таким образом, у вас будет прямоугольный треугольник [BEA], у которого мы знаем сторону AB и угол A; в этом треугольнике вычисляют BE, EA, и задача сводится к одному из предыдущих случаев; то есть к случаю, когда известны BE, CE; таким образом, мы будем знать BC и угол C, как мы объяснили.]
11. Например, у Карно, Лазар (1803 г.). Геометрия положения. ЖБМ Дюпра. п. 202.
12. Версия Java-апплета профессора Д. Э. Джойса из Университета Кларка.
13. Александр Богомольный приписывает это доказательство учителю Джону Молокачу (2011), но оно может быть старше. Богомольный, Александр . «Закон косинусов (независимый от теоремы Пифагора)». Разрежьте узел . Проверено 9 января 2024 г.
14. Кейси, Джон (1889). Трактат о сферической тригонометрии: и ее применении к геодезии и астрономии с многочисленными примерами . Лондон: Лонгманс, Грин и компания. п. 133.

Внешние ссылки

• «Теорема косинуса», Математическая энциклопедия , EMS Press , 2001 [1994]
• Несколько выводов закона косинуса, в том числе вывод Евклида при разрезании узла.
• Интерактивный апплет закона косинусов