Прямое восхождение (сокращенно RA ; символ α ) — угловое расстояние конкретной точки, измеренное на восток вдоль небесного экватора от Солнца в день мартовского равноденствия до ( часового круга ) рассматриваемой точки над Землей. [1] В сочетании со склонением эти астрономические координаты определяют местоположение точки на небесной сфере в экваториальной системе координат .
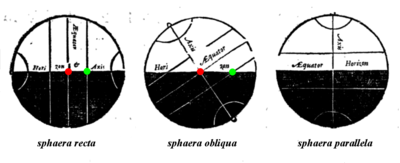
Старый термин, прямое восхождение ( лат . ascensio recta ) [ 2 ] относится к восхождению , или точке на небесном экваторе, которая поднимается вместе с любым небесным объектом , видимым с экватора Земли , где небесный экватор пересекает горизонт под прямым углом . Он контрастирует с косым восхождением , точкой на небесном экваторе, которая поднимается вместе с любым небесным объектом, видимым с большинства широт на Земле, где небесный экватор пересекает горизонт под косым углом . [3]


Прямое восхождение — это небесный эквивалент земной долготы . И прямое восхождение, и долгота измеряют угол от основного направления (нулевой точки) на экваторе . Прямое восхождение измеряется от Солнца в день мартовского равноденствия, т. е. от Первой точки Овна , которая является местом на небесной сфере , где Солнце пересекает небесный экватор с юга на север в день мартовского равноденствия и в настоящее время находится в созвездии Рыб . Прямое восхождение измеряется непрерывно по полному кругу от этого выравнивания Земли и Солнца в пространстве, этого равноденствия, измерение увеличивается к востоку. [4]
При наблюдении с Земли (за исключением полюсов) отмечено, что объекты, имеющие 12 ч прямого восхождения, дольше всего видны (появляются в течение ночи) в мартовское равноденствие; те, у которых 0 ч прямого восхождения (кроме Солнца), делают это в сентябрьское равноденствие. В эти даты в полночь такие объекты достигнут («кульминируют» в) своей наивысшей точки (своего меридиана). Насколько высоко, зависит от их склонения; если склонение 0° (т. е. на небесном экваторе ), то на экваторе Земли они находятся прямо над головой (в зените ).
Для прямого восхождения можно было бы выбрать любую угловую единицу , но обычно ее измеряют в часах ( ч ), минутах ( м ) и секундах ( с ), причем 24 ч эквивалентны полному кругу . Астрономы выбрали эту единицу для измерения прямого восхождения, потому что они измеряют местоположение звезды, измеряя время ее прохождения через самую высокую точку на небе при вращении Земли . Линия, проходящая через самую высокую точку на небе, называемая меридианом , является проекцией линии долготы на небесную сферу. Поскольку полный круг содержит 24 ч прямого восхождения или 360° ( градусов дуги ), 1/24 окружности измеряется как 1 час прямого восхождения, или 15°; 1/1440 окружности измеряется как 1 м прямого восхождения или 15 минут дуги (также пишется как 15′); и 1/86400 окружности содержит 1 с прямого восхождения или 15 секунд дуги (также пишется как 15″). Полный круг, измеренный в единицах прямого восхождения, содержит 24 × 60 × 60 =86 400 с , или 24 × 60 =1 440 м , или 24 ч . [5]
Поскольку прямые восхождения измеряются в часах ( вращении Земли ), их можно использовать для определения положения объектов на небе. Например, если звезда с RA = 1 ч 30 м 00 с находится на своем меридиане, то звезда с RA = 20 ч 00 м 00 с будет на/на своем меридиане (в своей кажущейся наивысшей точке) на 18,5 сидерических часов позже.
Звездный часовой угол, используемый в небесной навигации , похож на прямое восхождение, но увеличивается на запад, а не на восток. Обычно измеряется в градусах (°), является дополнением прямого восхождения по отношению к 24 ч . [6] Важно не путать звездный часовой угол с астрономическим понятием часового угла , который измеряет угловое расстояние объекта на запад от местного меридиана .
Ось Земли описывает небольшую окружность (относительно ее небесного экватора) медленно на запад вокруг небесных полюсов , совершая один цикл примерно за 26 000 лет. Это движение, известное как прецессия , заставляет координаты неподвижных небесных объектов непрерывно, хотя и довольно медленно, меняться. Поэтому экваториальные координаты (включая прямое восхождение) по своей сути являются относительными к году их наблюдения, и астрономы указывают их со ссылкой на конкретный год, известный как эпоха . Координаты из разных эпох должны быть математически повернуты, чтобы соответствовать друг другу или соответствовать стандартной эпохе. [7] Прямое восхождение для «неподвижных звезд» на экваторе увеличивается примерно на 3,1 секунды в год или 5,1 минуты за столетие, но для неподвижных звезд вдали от экватора скорость изменения может быть любой от отрицательной бесконечности до положительной бесконечности. (К этому следует добавить собственное движение звезды.) За цикл прецессии в 26 000 лет «неподвижные звезды», которые находятся далеко от полюсов эклиптики , увеличивают прямое восхождение на 24 ч, или примерно на 5,6' за столетие, тогда как звезды в пределах 23,5° от полюса эклиптики претерпевают чистое изменение на 0 ч. Прямое восхождение Полярной звезды быстро увеличивается — в 2000 г. н. э. оно составляло 2,5 ч, но когда она приблизится к северному небесному полюсу в 2100 г., ее прямое восхождение составит 6 ч. Северный полюс эклиптики в Драконе и Южный полюс эклиптики в Золотой Рыбе всегда имеют прямое восхождение 18 ч и 6 ч соответственно.
В настоящее время используется стандартная эпоха J2000.0 , которая приходится на 1 января 2000 года в 12:00 TT . Префикс "J" указывает на то, что это юлианская эпоха . До J2000.0 астрономы использовали последовательные бесселевские эпохи B1875.0, B1900.0 и B1950.0. [8]
Концепция прямого восхождения была известна по крайней мере еще со времен Гиппарха , который измерял звезды в экваториальных координатах во II веке до н. э. Однако Гиппарх и его последователи составляли свои звездные каталоги в эклиптических координатах , а использование прямого восхождения ограничивалось особыми случаями.
С изобретением телескопа астрономы получили возможность наблюдать небесные объекты более подробно, при условии, что телескоп можно было удерживать направленным на объект в течение определенного периода времени. Самый простой способ сделать это — использовать экваториальную монтировку , которая позволяет выровнять телескоп с одним из двух его шарниров параллельно оси Земли. Моторизованный часовой привод часто используется с экваториальной монтировкой, чтобы компенсировать вращение Земли . Поскольку экваториальная монтировка стала широко использоваться для наблюдений, в то же время для простоты была принята экваториальная система координат, которая включает прямое восхождение. Затем экваториальные монтировки можно было точно наводить на объекты с известным прямым восхождением и склонением с помощью установочных кругов . Первым звездным каталогом, в котором использовались прямое восхождение и склонение, была Historia Coelestis Britannica Джона Флемстида (1712, 1725).
