Анализ выживаемости

Отделение статистики

Анализ выживаемости — это раздел статистики , посвященный анализу ожидаемой продолжительности времени до наступления одного события, например, смерти в биологических организмах и отказа в механических системах. Эта тема называется теорией надежности , анализом надежности или инженерией надежности в инженерии , анализом продолжительности или моделированием продолжительности в экономике и анализом истории событий в социологии . Анализ выживаемости пытается ответить на определенные вопросы, например, какова доля популяции, которая выживет после определенного времени? Из тех, кто выживет, с какой скоростью они умрут или выйдут из строя? Можно ли учитывать несколько причин смерти или отказа? Как определенные обстоятельства или характеристики увеличивают или уменьшают вероятность выживания ?

Чтобы ответить на такие вопросы, необходимо определить «продолжительность жизни». В случае биологического выживания смерть однозначна, но для механической надежности отказ может быть нечетко определен, поскольку вполне могут быть механические системы, в которых отказ является частичным, вопросом степени или иным образом не локализован во времени . Даже в биологических проблемах некоторые события (например, сердечный приступ или отказ другого органа) могут иметь ту же самую неоднозначность. Теория , изложенная ниже, предполагает четко определенные события в определенное время; другие случаи могут лучше рассматриваться с помощью моделей, которые явно учитывают неоднозначные события.

В более общем смысле анализ выживания включает моделирование данных времени до события; в этом контексте смерть или отказ считаются «событием» в литературе по анализу выживания — традиционно для каждого субъекта происходит только одно событие, после которого организм или механизм умирает или ломается. Модели повторяющихся событий или повторяющихся событий ослабляют это предположение. Изучение повторяющихся событий актуально для надежности систем , а также во многих областях социальных наук и медицинских исследований.

Введение в анализ выживаемости

Анализ выживаемости используется несколькими способами:

• Для описания времени выживания членов группы
  • Таблицы продолжительности жизни
  • Кривые Каплана–Майера
  • Функция выживания
  • Функция опасности
• Сравнить время выживания двух или более групп
  • Логранговый тест
• Описать влияние категориальных или количественных переменных на выживаемость
  • Регрессия пропорциональных рисков Кокса
  • Параметрические модели выживания
  • Деревья выживания
  • Выживание случайных лесов

Определения общих терминов в анализе выживаемости

В анализах выживаемости обычно используются следующие термины:

• Событие: смерть, возникновение заболевания, рецидив заболевания, выздоровление или другой интересующий опыт
• Время: время от начала периода наблюдения (например, хирургического вмешательства или начала лечения) до (i) события, или (ii) окончания исследования, или (iii) потери контакта или выхода из исследования.
• Цензурирование / Цензурированное наблюдение: Цензурирование происходит, когда у нас есть некоторая информация об индивидуальном времени выживания, но мы не знаем точное время выживания. Субъект цензурируется в том смысле, что ничего не наблюдается или не известно о нем после времени цензурирования. Цензурированный субъект может иметь или не иметь событие после окончания времени наблюдения.
• Функция выживания S(t): вероятность того, что субъект проживет дольше времени t.

Пример: данные о выживаемости при остром миелоидном лейкозе

В этом примере используется набор данных по выживаемости при остром миелоидном лейкозе «aml» из пакета «survival» в R. Набор данных взят из Miller (1997) ^[1] , и вопрос заключается в том, следует ли продлевать («поддерживать») стандартный курс химиотерапии для дополнительных циклов.

Набор данных AML, отсортированный по времени выживания, показан в поле.

• Время обозначается переменной «время», которая является временем выживания или цензурирования.
• Событие (рецидив рака ОМЛ) обозначается переменной «статус». 0  = нет события (цензурировано), 1  = событие (рецидив)
• Группа лечения: переменная «x» указывает, проводилась ли поддерживающая химиотерапия.

Последнее наблюдение (11) на 161 неделе цензурировано. Цензурирование указывает на то, что у пациента не было события (отсутствие рецидива рака aml). Другой субъект, наблюдение 3, был цензурирован на 13 неделе (обозначено статусом = 0). Этот субъект находился в исследовании всего 13 недель, и рак aml не рецидивировал в течение этих 13 недель. Возможно, что этот пациент был включен в исследование ближе к концу, поэтому его можно было наблюдать только 13 недель. Также возможно, что пациент был включен в исследование на ранней стадии, но был потерян для последующего наблюдения или выбыл из исследования. Таблица показывает, что другие субъекты были цензурированы на 16, 28 и 45 неделе (наблюдения 17, 6 и  9 со статусом = 0). У всех остальных субъектов произошли события (рецидив рака aml) во время участия в исследовании. Интерес представляет вопрос о том, наступает ли рецидив у пациентов, находящихся на поддерживающей терапии, позже, чем у пациентов, не находящихся на поддерживающей терапии.

График Каплана–Майера для данных AML

Функция выживания S ( t ) — это вероятность того, что субъект проживет дольше времени t . S ( t ) теоретически является гладкой кривой, но обычно ее оценивают с помощью кривой Каплана–Майера (КМ). На графике показан график КМ для данных aml, и его можно интерпретировать следующим образом:

• Ось x — это время от нуля (когда началось наблюдение) до последней наблюдаемой точки времени.
• Ось Y — доля выживших субъектов. В нулевой момент времени 100% субъектов живы без какого-либо события.
• Сплошная линия (похожая на лестницу) показывает последовательность возникновения событий.
• Вертикальное падение указывает на событие. В таблице aml, показанной выше, у двух субъектов были события на пятой неделе, у двух были события на восьмой неделе, у одного было событие на девятой неделе и т. д. Эти события на пятой неделе, восьмой неделе и т. д. обозначены вертикальными падениями на графике KM в эти временные точки.
• На самом правом конце графика KM есть отметка на 161 неделе. Вертикальная отметка указывает на то, что пациентка была цензурирована в это время. В таблице данных aml пять субъектов были цензурированы на 13, 16, 28, 45 и 161 неделе. На графике KM есть пять отметок, соответствующих этим цензурированным наблюдениям.

Таблица продолжительности жизни для данных AML

Таблица жизни суммирует данные о выживании с точки зрения количества событий и доли выживших в каждой точке времени события.  Показана таблица жизни для данных aml, созданная с помощью программного обеспечения R.

Таблица жизни суммирует события и долю выживших в каждой точке времени события. Столбцы в таблице жизни имеют следующую интерпретацию:

• время указывает временные точки, в которые происходят события.
• n.risk — это количество субъектов, находящихся в группе риска непосредственно перед моментом времени t. «Риск» означает, что у субъекта не было события до момента времени t, и он не подвергался цензуре до или во время t.
• n.event — количество субъектов, у которых произошли события в момент времени t.
• выживаемость — это доля выживших, определяемая с помощью оценки предела произведения Каплана–Майера.
• std.err — стандартная ошибка оценки выживаемости. Стандартная ошибка оценки предела произведения Каплана–Майера рассчитывается с использованием формулы Гринвуда и зависит от числа подверженных риску (n.risk в таблице), числа смертей (n.event в таблице) и доли выживших (survival в таблице).
• нижний 95% ДИ и верхний 95% ДИ представляют собой нижнюю и верхнюю 95% доверительные границы для доли выживших.

Логранговый тест: Тестирование различий в выживаемости в данных AML

Тест лог-ранга сравнивает время выживания двух или более групп. В этом примере используется тест лог-ранга для разницы в выживании в группах с поддерживаемым и неподдерживаемым лечением в данных AML. На графике показаны графики KM для данных AML, разбитых по группам лечения, что обозначено переменной «x» в данных.

График Каплана–Майера по группам лечения в ОМЛ

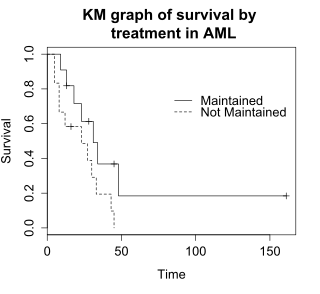
Нулевая гипотеза для логрангового теста заключается в том, что группы имеют одинаковую выживаемость. Ожидаемое число субъектов, выживающих в каждой точке времени в каждой из них, корректируется с учетом числа субъектов, находящихся в группе риска, в группах в каждое время события. Логранговый тест определяет, значительно ли отличается наблюдаемое число событий в каждой группе от ожидаемого числа. Формальный тест основан на статистике хи-квадрат. Когда логранговая статистика велика, это свидетельствует о разнице во времени выживания между группами. Логранговая статистика приблизительно имеет распределение хи-квадрат с одной степенью свободы, а p-значение рассчитывается с использованием критерия хи-квадрат .

Для данных примера логранговый тест на разницу в выживаемости дает p-значение p=0,0653, что указывает на то, что группы лечения не имеют существенных различий в выживаемости, предполагая уровень альфа 0,05. Размер выборки из 23 субъектов скромен, поэтому мало возможностей для обнаружения различий между группами лечения. Тест хи-квадрат основан на асимптотическом приближении, поэтому к p-значению следует относиться с осторожностью для небольших размеров выборки .

Регрессионный анализ пропорциональных рисков Кокса (PH)

Кривые Каплана–Майера и логранговые тесты наиболее полезны, когда предикторная переменная является категориальной (например, препарат против плацебо) или принимает небольшое количество значений (например, дозы препарата 0, 20, 50 и 100 мг/день), которые можно рассматривать как категориальные. Логранговый тест и кривые КМ не работают легко с количественными предикторами, такими как экспрессия генов, количество лейкоцитов или возраст. Для количественных предикторных переменных альтернативным методом является регрессионный анализ пропорциональных рисков Кокса . Модели Кокса PH также работают с категориальными предикторными переменными, которые кодируются как индикаторные или фиктивные переменные {0,1}. Логранговый тест является особым случаем анализа Кокса PH и может быть выполнен с помощью программного обеспечения Кокса PH.

Пример: регрессионный анализ пропорциональных рисков Кокса для меланомы

В этом примере используется набор данных по меланоме из главы 14 Далгаарда. ^[2]

Данные находятся в пакете R ISwR. Регрессия пропорциональных рисков Кокса с использованием  R дает результаты, показанные в рамке.

Выходные данные регрессии пропорциональных рисков Кокса для данных по меланоме. Предикторная переменная — пол 1: женский, 2: мужской.

Результаты регрессии Кокса интерпретируются следующим образом.

• Пол кодируется как числовой вектор (1: женский, 2: мужской).  Сводка R для модели Кокса дает отношение рисков (HR) для второй группы относительно первой группы, то есть мужчины против женщин.
• coef = 0,662 — предполагаемый логарифм отношения рисков для мужчин и женщин.
• exp(coef) = 1,94 = exp(0,662) - Логарифм отношения рисков (coef= 0,662) преобразуется в отношение рисков с использованием exp(coef). Сводка для модели Кокса дает отношение рисков для второй группы относительно первой группы, то есть мужчины против женщин. Оценочное отношение рисков 1,94 указывает на то, что у мужчин более высокий риск смерти (более низкие показатели выживаемости), чем у женщин, в этих данных.
• se(coef) = 0,265 — стандартная ошибка логарифмического отношения рисков.
• z = 2,5 = coef/se(coef) = 0,662/0,265. Разделив coef на его стандартную ошибку, получим z-оценку.
• p=0,013. Значение p, соответствующее z=2,5 для пола, равно p=0,013, что указывает на значительную разницу в выживаемости в зависимости от пола.

В сводном выводе также приводятся верхний и нижний 95% доверительные интервалы для коэффициента риска: нижняя 95% граница = 1,15; верхняя 95% граница = 3,26.

Наконец, вывод дает p-значения для трех альтернативных тестов общей значимости модели:

• Тест отношения правдоподобия = 6,15 на 1 df, p=0,0131
• Тест Вальда = 6,24 на 1 df, p=0,0125
• Результат (логарифмический ранг) теста = 6,47 на 1 df, p=0,0110

Эти три теста асимптотически эквивалентны. Для достаточно больших N они дадут схожие результаты. Для малых N они могут несколько отличаться. Последняя строка, «Score (logrank) test» — это результат для логрангового теста с p=0,011, тот же результат, что и логранговый тест, поскольку логранговый тест является особым случаем регрессии Кокса PH. Тест отношения правдоподобия имеет лучшее поведение для небольших размеров выборки, поэтому он, как правило, предпочтителен.

Модель Кокса с использованием ковариаты в данных по меланоме

Модель Кокса расширяет логранговый тест, позволяя включать дополнительные ковариаты. ^[3] В этом примере используется набор данных меланомы, где предикторные переменные включают непрерывный ковариат, толщину опухоли (имя переменной = «толстая»).

Гистограммы толщины опухоли меланомы

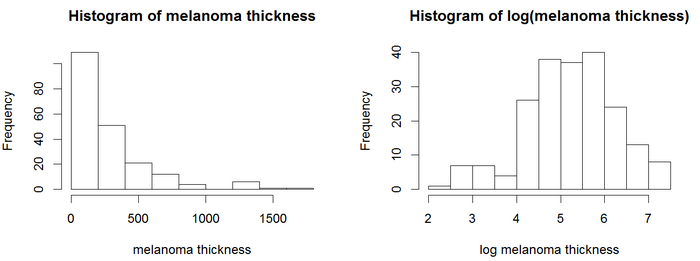
В гистограммах значения толщины положительно скошены и не имеют гауссово -подобного, симметричного распределения вероятностей . Регрессионные модели, включая модель Кокса, обычно дают более надежные результаты с нормально распределенными переменными. ^{[ необходима цитата ]} Для этого примера мы можем использовать логарифмическое преобразование. Логарифм толщины опухоли выглядит более нормально распределенным, поэтому модели Кокса будут использовать логарифм толщины. Анализ PH Кокса дает результаты в поле.

Вывод PH Кокса для набора данных меланомы с ковариацией логарифма толщины опухоли

Значение p для всех трех общих тестов (вероятность, Вальд и оценка) является значимым, что указывает на значимость модели. Значение p для log(thick) составляет 6,9e-07, с отношением рисков HR = exp(coef) = 2,18, что указывает на сильную связь между толщиной опухоли и повышенным риском смерти.

Напротив, p-значение для пола теперь p=0,088. Коэффициент риска HR = exp(coef) = 1,58 с 95% доверительным интервалом от 0,934 до 2,68. Поскольку доверительный интервал для HR включает 1, эти результаты указывают на то, что пол вносит меньший вклад в разницу в HR после учета толщины опухоли и только тенденцию к значимости. Изучение графиков log(толщины) по полу и t-теста log(толщины) по полу указывают на то, что существует значительная разница между мужчинами и женщинами в толщине опухоли, когда они впервые обращаются к врачу.

Модель Кокса предполагает, что опасности пропорциональны. Предположение о пропорциональности опасности можно проверить с помощью  функции R cox.zph(). Значение p, меньшее 0,05, указывает на то, что опасности не пропорциональны. Для данных по меланоме мы получаем p=0,222. Следовательно, мы не можем отвергнуть нулевую гипотезу о пропорциональности опасностей. Дополнительные тесты и графики для проверки модели Кокса описаны в цитируемых учебниках.

Расширения моделей Кокса

Модели Кокса можно расширить для учета вариаций простого анализа.

• Стратификация. Субъекты могут быть разделены на слои, где субъекты внутри слоя, как ожидается, будут относительно более похожи друг на друга, чем на случайно выбранных субъектов из других слоев. Предполагается, что параметры регрессии одинаковы во всех слоях, но для каждого слоя может существовать разная базовая опасность. Стратификация полезна для анализов с использованием подобранных субъектов, для работы с подгруппами пациентов, такими как разные клиники, и для работы с нарушениями предположения о пропорциональной опасности.
• Изменяющиеся во времени ковариаты. Некоторые переменные, такие как пол и группа лечения, обычно остаются неизменными в клиническом исследовании. Другие клинические переменные, такие как уровень сывороточного белка или доза сопутствующих лекарств, могут меняться в ходе исследования. Модели Кокса могут быть расширены для таких изменяющихся во времени ковариатов.

Древовидные модели выживания

Модель регрессии Кокса PH является линейной моделью. Она похожа на линейную регрессию и логистическую регрессию. В частности, эти методы предполагают, что для разделения групп (живые, мертвые) или для оценки количественного ответа (время выживания) достаточно одной линии, кривой, плоскости или поверхности.

В некоторых случаях альтернативные разбиения дают более точную классификацию или количественные оценки. Один из наборов альтернативных методов — это древовидные модели выживания, ^{[4] [5] [6],} включая случайные леса выживания. ^[7] Древовидные модели выживания могут давать более точные прогнозы, чем модели Кокса. Изучение обоих типов моделей для заданного набора данных — разумная стратегия.

Пример анализа дерева выживания

В этом примере анализа дерева выживаемости используется  пакет R "rpart". ^[8] Пример основан на 146  пациентах с раком простаты стадии C в наборе данных stagec в rpart. Rpart и пример stagec описаны в Atkinson and Therneau (1997), ^[9] , который также распространяется как виньетка пакета rpart. ^[8]

Переменные на этапах:

• pgtime : время до прогрессирования или последнего наблюдения без прогрессирования
• pgstat : статус на момент последнего наблюдения (1=выполнено, 0=отцензурировано)
• возраст : возраст на момент постановки диагноза
• eet : ранняя эндокринная терапия (1=нет, 0=да)
• плоидность : диплоидный/тетраплоидный/анеуплоидный ДНК-рисунок
• g2 : % клеток в фазе G2
• степень : степень опухоли (1-4)
• Глисон : оценка по шкале Глисона (3-10)

Полученное в результате анализа дерево выживания показано на рисунке.

Дерево выживаемости для набора данных рака простаты

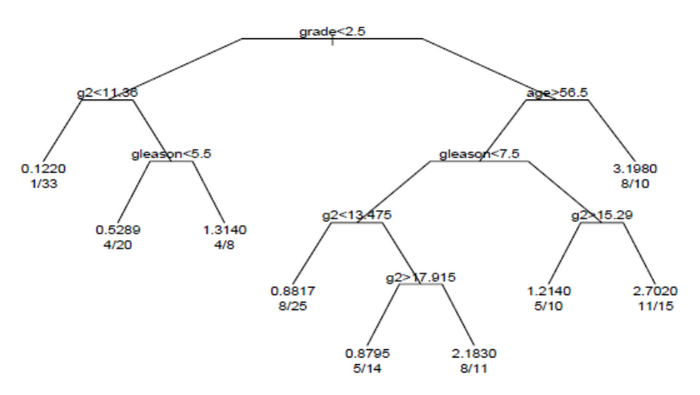
Каждая ветвь в дереве указывает на разделение по значению переменной. Например, корень дерева разделяет субъектов с оценкой < 2,5 против субъектов с оценкой 2,5 или выше. Конечные узлы указывают количество субъектов в узле, количество субъектов, у которых есть события, и относительную частоту событий по сравнению с корнем. В узле слева значения 1/33 указывают, что у одного из 33 субъектов в узле было событие, и что относительная частота событий составляет 0,122. В узле справа внизу значения 11/15 указывают, что у 11 из 15 субъектов в узле было событие, и относительная частота событий составляет 2,7.

Выживание случайных лесов

Альтернативой построению одного дерева выживания является построение множества деревьев выживания, где каждое дерево строится с использованием выборки данных, и усреднение деревьев для прогнозирования выживания. ^[7] Это метод, лежащий в основе моделей случайного леса выживания. Анализ случайного леса выживания доступен в  пакете R "randomForestSRC". ^[10]

Пакет randomForestSRC включает в себя пример анализа случайного леса выживаемости с использованием набора данных pbc. Эти данные взяты из исследования первичного билиарного цирроза печени (PBC) клиники Майо, проведенного между 1974 и 1984 годами. В этом примере модель выживания случайного леса дает более точные прогнозы выживаемости, чем модель Cox PH. Ошибки прогнозирования оцениваются с помощью повторной выборки bootstrap .

Модели выживания на основе глубокого обучения

Недавние достижения в глубоком репрезентативном обучении были распространены на оценку выживаемости. Модель DeepSurv ^[11] предлагает заменить логарифмически линейную параметризацию модели CoxPH на многослойный персептрон. Дальнейшие расширения, такие как Deep Survival Machines ^[12] и Deep Cox Mixtures ^[13], включают использование моделей смесей скрытых переменных для моделирования распределения времени до события как смеси параметрических или полупараметрических распределений при совместном обучении представлений входных ковариатов. Подходы глубокого обучения показали превосходную производительность, особенно на сложных модальностях входных данных, таких как изображения и клинические временные ряды.

Общая формулировка

Функция выживания

Объектом первостепенного интереса является функция выживания , условно обозначаемая S , которая определяется как

$${\displaystyle S(t)=\Pr(T>t)}$$где t — некоторое время, T — случайная величина, обозначающая время смерти, а «Pr» означает вероятность . То есть функция выживания — это вероятность того, что время смерти наступит позже некоторого указанного времени t . Функция выживания также называется функцией выживания или функцией выживаемости в задачах биологического выживания и функцией надежности в задачах механического выживания. В последнем случае функция надежности обозначается R ( t ).

Обычно предполагается, что S (0) = 1, хотя оно может быть меньше 1,  если существует вероятность немедленной смерти или отказа.

Функция выживания должна быть невозрастающей: S ( u ) ≤ S ( t ), если u ≥ t . Это свойство следует непосредственно, поскольку T > u подразумевает T > t . Это отражает представление о том, что выживание до более позднего возраста возможно только в том случае, если достигнуты все более молодые возрасты. Учитывая это свойство, функция распределения продолжительности жизни и плотность событий ( F и f ниже) хорошо определены.

Обычно предполагается, что функция выживания стремится к нулю по мере увеличения возраста без ограничений (т. е. S ( t ) → 0 при t → ∞), хотя предел может быть больше нуля, если вечная жизнь возможна. Например, мы могли бы применить анализ выживания к смеси стабильных и нестабильных изотопов углерода ; нестабильные изотопы рано или поздно распадутся, но стабильные изотопы будут существовать бесконечно.

Функция распределения времени жизни и плотность событий

Соответствующие величины определяются в терминах функции выживания.

Функция распределения продолжительности жизни , условно обозначаемая F , определяется как дополнение функции выживания,

$${\displaystyle F(t)=\Pr(T\leq t)=1-S(t).}$$Если F дифференцируема , то производная, которая является функцией плотности распределения времени жизни, условно обозначается f ,

$${\displaystyle f(t)=F'(t)={\frac {d}{dt}}F(t).}$$Функцию f иногда называют плотностью событий ; это частота случаев смерти или отказа за единицу времени.

Функцию выживания можно выразить через функции распределения вероятностей и плотности вероятности.

$${\displaystyle S(t)=\Pr(T>t)=\int _{t}^{\infty }f(u)\,du=1-F(t).}$$Аналогично, функцию плотности событий выживания можно определить как

$${\displaystyle s(t)=S'(t)={\frac {d}{dt}}S(t)={\frac {d}{dt}}\int _{t}^{\infty }f(u)\,du={\frac {d}{dt}}[1-F(t)]=-f(t).}$$В других областях, таких как статистическая физика, функция плотности событий выживания известна как плотность времени первого прохождения .

Функция опасности и кумулятивная функция опасности

Функция опасности , условно обозначаемая или , определяется как частота событий в момент времени, обусловленная выживанием до момента времени или позже (то есть ). Предположим, что элемент выжил в течение некоторого времени , и мы хотим получить вероятность того, что он не выживет в течение дополнительного времени : ${\displaystyle \lambda }$ ${\displaystyle h}$ ${\displaystyle t}$ ${\displaystyle t}$ ${\displaystyle T\geq t}$ ${\displaystyle t}$ ${\displaystyle dt}$

$${\displaystyle h(t)=\lim _{dt\rightarrow 0}{\frac {\Pr(t\leq T<t+dt)}{dt\cdot S(t)}}={\frac {f(t)}{S(t)}}=-{\frac {S'(t)}{S(t)}}.}$$Сила смертности является синонимом функции риска , которая используется, в частности, в демографии и актуарной науке , где она обозначается как . Термин «уровень риска» является еще одним синонимом. ${\displaystyle \mu }$

Сила смертности функции выживания определяется как ${\displaystyle \mu (x)=-{d \over dx}\ln(S(x))={\frac {f(x)}{S(x)}}}$

Сила смертности также называется силой отказа. Это функция плотности вероятности распределения смертности.

В актуарной науке уровень риска — это уровень смертности для жизней в возрасте . Для жизни в возрасте , сила смертности лет спустя — это сила смертности для -летнего. Уровень риска также называется уровнем отказов. Уровень риска и уровень отказов — это названия, используемые в теории надежности. ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle t}$ ${\displaystyle (x+t)}$

Любая функция является функцией опасности тогда и только тогда, когда она удовлетворяет следующим свойствам: ${\displaystyle h}$

1. ${\displaystyle \forall x\geq 0\left(h(x)\geq 0\right)}$,
2. ${\displaystyle \int _{0}^{\infty }h(x)dx=\infty }$.

Фактически, коэффициент риска обычно более информативен относительно основного механизма отказа, чем другие представления распределения срока службы.

Функция опасности должна быть неотрицательной, , а ее интеграл по должен быть бесконечным, но не ограниченным иным образом; она может быть возрастающей или убывающей, немонотонной или прерывистой. Примером является функция опасности кривой ванны , которая велика для малых значений , уменьшается до некоторого минимума, а затем снова увеличивается; это может моделировать свойство некоторых механических систем либо выходить из строя вскоре после эксплуатации, либо гораздо позже, по мере старения системы. ${\displaystyle \lambda (t)\geq 0}$ ${\displaystyle [0,\infty ]}$ ${\displaystyle t}$

Функцию опасности можно альтернативно представить в терминах кумулятивной функции опасности , условно обозначаемой или : ${\displaystyle \Lambda }$ ${\displaystyle H}$

$${\displaystyle \,\Lambda (t)=-\log S(t)}$$поэтому перестановка знаков и возведение в степень

$${\displaystyle \,S(t)=\exp(-\Lambda (t))}$$или дифференцируя (с цепным правилом)

$${\displaystyle {\frac {d}{dt}}\Lambda (t)=-{\frac {S'(t)}{S(t)}}=\lambda (t).}$$Название «кумулятивная функция риска» происходит от того факта, что

$${\displaystyle \Lambda (t)=\int _{0}^{t}\lambda (u)\,du}$$что представляет собой «накопление» опасности с течением времени.

Из определения мы видим, что она неограниченно возрастает, когда t стремится к бесконечности (предполагая, что стремится к нулю). Это подразумевает, что не должно уменьшаться слишком быстро, поскольку по определению кумулятивный риск должен расходиться. Например, не является функцией риска любого распределения выживания, поскольку его интеграл сходится к 1. ${\displaystyle \Lambda (t)}$ ${\displaystyle S(t)}$ ${\displaystyle \lambda (t)}$ ${\displaystyle \exp(-t)}$

Функция выживания , кумулятивная функция риска , плотность , функция риска и функция распределения времени жизни связаны соотношением ${\displaystyle S(t)}$ ${\displaystyle \Lambda (t)}$ ${\displaystyle f(t)}$ ${\displaystyle \lambda (t)}$ ${\displaystyle F(t)}$ $${\displaystyle S(t)=\exp[-\Lambda (t)]={\frac {f(t)}{\lambda (t)}}=1-F(t),\quad t>0.}$$

Величины, полученные из распределения выживаемости

Будущая продолжительность жизни в данный момент времени — это время, оставшееся до смерти, учитывая выживаемость до возраста . Таким образом, это в настоящей нотации. Ожидаемая будущая продолжительность жизни — это ожидаемое значение будущей продолжительности жизни. Вероятность смерти в возрасте или до него , учитывая выживаемость до возраста , равна просто ${\displaystyle t_{0}}$ ${\displaystyle t_{0}}$ ${\displaystyle T-t_{0}}$ ${\displaystyle t_{0}+t}$ ${\displaystyle t_{0}}$

$${\displaystyle P(T\leq t_{0}+t\mid T>t_{0})={\frac {P(t_{0}<T\leq t_{0}+t)}{P(T>t_{0})}}={\frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}.}$$Следовательно, плотность вероятности будущей жизни равна

$${\displaystyle {\frac {d}{dt}}{\frac {F(t_{0}+t)-F(t_{0})}{S(t_{0})}}={\frac {f(t_{0}+t)}{S(t_{0})}}}$$и ожидаемая будущая продолжительность жизни составляет

$${\displaystyle {\frac {1}{S(t_{0})}}\int _{0}^{\infty }t\,f(t_{0}+t)\,dt={\frac {1}{S(t_{0})}}\int _{t_{0}}^{\infty }S(t)\,dt,}$$где второе выражение получено с помощью интегрирования по частям .

Для , то есть при рождении, это сводится к ожидаемой продолжительности жизни. ${\displaystyle t_{0}=0}$

В задачах надежности ожидаемый срок службы называется средним временем до отказа , а ожидаемый будущий срок службы называется средним остаточным сроком службы .

Поскольку вероятность дожития особи до возраста t или дольше равна S ( t ), по определению, ожидаемое число выживших в возрасте t из исходной популяции из n новорожденных равно n × S ( t ), предполагая одинаковую функцию выживания для всех особей. Таким образом, ожидаемая доля выживших равна S ( t ). Если выживание разных особей независимо, число выживших в возрасте t имеет биномиальное распределение с параметрами n и S ( t ), а дисперсия доли выживших равна S ( t ) × (1- S ( t ))/ n .

Возраст, в котором остается определенная доля выживших, можно найти, решив уравнение S ( t ) = q для t , где q — рассматриваемый квантиль . Обычно интерес представляет медианная продолжительность жизни , для которой q = 1/2, или другие квантили, такие как q = 0,90 или q = 0,99.

Цензура

Цензурирование — это форма проблемы с отсутствующими данными, при которой время до события не наблюдается по таким причинам, как прекращение исследования до того, как все набранные субъекты продемонстрировали интересующее событие, или субъект покинул исследование до того, как произошло событие. Цензурирование распространено в анализе выживаемости.

Если известен только нижний предел l для истинного времени события T , такой что T > l , это называется правым цензурированием . Правое цензурирование будет иметь место, например, для тех субъектов, чья дата рождения известна, но которые все еще живы, когда они потеряны для последующего наблюдения или когда исследование заканчивается. Мы обычно сталкиваемся с данными, цензурированными справа.

Если интересующее событие уже произошло до того, как субъект был включен в исследование, но неизвестно, когда оно произошло, то говорят, что данные подвергнуты левой цензуре . ^[14] Когда можно сказать только, что событие произошло между двумя наблюдениями или обследованиями, это интервальная цензура .

Левое цензурирование происходит, например, когда постоянный зуб уже появился до начала стоматологического исследования, направленного на оценку распределения его появления. В том же исследовании время появления цензурируется по интервалу, когда постоянный зуб присутствует во рту при текущем обследовании, но еще не присутствует при предыдущем обследовании. Интервальное цензурирование часто происходит в исследованиях ВИЧ/СПИДа. Действительно, время до сероконверсии ВИЧ можно определить только с помощью лабораторной оценки, которая обычно начинается после визита к врачу. Тогда можно сделать вывод, что сероконверсия ВИЧ произошла только между двумя обследованиями. То же самое относится к диагностике СПИДа, которая основана на клинических симптомах и должна быть подтверждена медицинским обследованием.

Также может случиться, что субъекты с продолжительностью жизни меньше некоторого порога могут вообще не наблюдаться: это называется усечением . Обратите внимание, что усечение отличается от левого цензурирования, поскольку для левого цензурированного данных мы знаем, что субъект существует, но для усеченного данных мы можем вообще не знать о субъекте. Усечение также распространено. В так называемом исследовании с отложенным входом субъекты вообще не наблюдаются, пока они не достигнут определенного возраста. Например, люди могут не наблюдаться, пока они не достигнут возраста поступления в школу. Любые умершие субъекты в дошкольной возрастной группе будут неизвестны. Данные, усеченные слева, распространены в актуарной работе для страхования жизни и пенсий . ^[15]

Данные с левой цензурой могут возникнуть, когда время выживания человека становится неполным на левой стороне периода наблюдения за человеком. Например, в эпидемиологическом примере мы можем контролировать пациента на предмет инфекционного заболевания, начиная с того времени, когда он или она получает положительный результат теста на инфекцию. Хотя мы можем знать правую сторону интересующей нас продолжительности, мы никогда не узнаем точное время воздействия инфекционного агента. ^[16]

Подгонка параметров к данным

Модели выживания можно рассматривать как обычные регрессионные модели, в которых переменной отклика является время. Однако вычисление функции правдоподобия (необходимой для подгонки параметров или выполнения других видов выводов) осложняется цензурированием. Функция правдоподобия для модели выживания при наличии цензурированных данных формулируется следующим образом. По определению функция правдоподобия — это условная вероятность данных при заданных параметрах модели. Принято считать, что данные независимы при заданных параметрах. Тогда функция правдоподобия — это произведение правдоподобия каждого элемента данных. Удобно разделить данные на четыре категории: нецензурированные, левоцензурированные, правоцензурированные и интервально цензурированные. Они обозначены как «unc.», «lc», «rc» и «ic» в уравнении ниже.

$${\displaystyle L(\theta )=\prod _{T_{i}\in unc.}\Pr(T=T_{i}\mid \theta )\prod _{i\in l.c.}\Pr(T<T_{i}\mid \theta )\prod _{i\in r.c.}\Pr(T>T_{i}\mid \theta )\prod _{i\in i.c.}\Pr(T_{i,l}<T<T_{i,r}\mid \theta ).}$$Для нецензурированных данных, равных возрасту смерти, имеем ${\displaystyle T_{i}}$

$${\displaystyle \Pr(T=T_{i}\mid \theta )=f(T_{i}\mid \theta ).}$$Для данных, цензурированных слева, таких, что известно, что возраст на момент смерти меньше , мы имеем ${\displaystyle T_{i}}$

$${\displaystyle \Pr(T<T_{i}\mid \theta )=F(T_{i}\mid \theta )=1-S(T_{i}\mid \theta ).}$$Для данных, цензурированных справа, таких, что известно, что возраст на момент смерти больше , мы имеем ${\displaystyle T_{i}}$

$${\displaystyle \Pr(T>T_{i}\mid \theta )=1-F(T_{i}\mid \theta )=S(T_{i}\mid \theta ).}$$Для интервала цензурированных данных, такого, что известно, что возраст на момент смерти меньше и больше , мы имеем ${\displaystyle T_{i,r}}$ ${\displaystyle T_{i,l}}$

$${\displaystyle \Pr(T_{i,l}<T<T_{i,r}\mid \theta )=S(T_{i,l}\mid \theta )-S(T_{i,r}\mid \theta ).}$$Важным приложением, в котором возникают данные, цензурированные по интервалу, являются данные о текущем состоянии, когда известно, что событие не произошло до времени наблюдения и произошло до времени следующего наблюдения. ${\displaystyle T_{i}}$

Непараметрическая оценка

Оценщик Каплана –Майера может использоваться для оценки функции выживания. Оценщик Нельсона–Аалена может использоваться для предоставления непараметрической оценки кумулятивной функции уровня риска. Эти оценщики требуют данных о продолжительности жизни. Периодические подсчеты случаев (когорты) и смертей (и выздоровлений) статистически достаточны для непараметрических оценок максимального правдоподобия и наименьших квадратов функций выживания без данных о продолжительности жизни.

Модели выживания в дискретном времени

В то время как многие параметрические модели предполагают непрерывное время, дискретные модели выживания могут быть сопоставлены с проблемой бинарной классификации. В дискретной модели выживания период выживания искусственно перевыбирается в интервалах, где для каждого интервала регистрируется бинарный целевой индикатор, если событие происходит в определенном временном горизонте. ^[17] Если бинарный классификатор (потенциально улучшенный с другой вероятностью, чтобы учитывать больше структуры проблемы) калибруется , то оценка классификатора является функцией опасности (т. е. условной вероятностью отказа). ^[17]

Описание преобразования данных о выживании в непрерывном времени в данные о выживании в дискретном времени. Индивидуум 4 цензурируется, а для индивидуума 5 событие происходит за пределами окна наблюдения 5.

Модели выживания в дискретном времени связаны с эмпирической вероятностью . ^{[18] [19]}

Качество соответствия

Степень соответствия моделей выживания можно оценить с помощью правил подсчета баллов . ^[20]

Компьютерное программное обеспечение для анализа выживаемости

В учебнике Кляйнбаума есть примеры анализа выживаемости с использованием SAS, R и других пакетов. ^[21] В учебниках Брострома ^[22] , Далгаарда ^[2] и Тейблмана и Кима ^[23] приведены примеры анализа выживаемости с использованием R (или с использованием S, и которые выполняются в R).

Распределения, используемые в анализе выживаемости

• Экспоненциальное распределение
• Распределение Вейбулла
• Логистическое распределение
• Гамма-распределение
• Экспоненциально-логарифмическое распределение
• Обобщенное гамма-распределение
• Гипертабастное распределение

Приложения

• Кредитный риск ^{[24] [25]}
• Уровень ложных обвинений заключенных, приговоренных к смертной казни ^[26]
• Сроки поставки металлических компонентов в аэрокосмической промышленности ^[27]
• Предикторы рецидивизма преступлений ^[28]
• Распределение выживаемости радиомеченых животных ^[29]
• Время насильственной смерти римских императоров ^[30]
• Межторговые интервалы ожидания для акций , торгуемых в электронном виде на фондовой бирже ^[31]

Смотрите также

• Модель ускоренного времени отказа
• Байесовский анализ выживаемости
• Кривая выживаемости клеток
• Цензурирование (статистика)
• Выбор портфеля с ограничениями по шансам
• Коэффициент отказов
• Частота превышения
• Оценка Каплана–Майера
• Тест логранга
• Максимальная вероятность
• Уровень смертности
• Среднее время безотказной работы
• Модели пропорциональных опасностей
• Теория надежности
• Время пребывания (статистика)
• Анализ последовательности в социальных науках
• Функция выживания
• Коэффициент выживаемости
• Дискретные по времени пропорциональные опасности

Ссылки

1. Миллер, Руперт Г. (1997), Анализ выживания , John Wiley & Sons, ISBN 0-471-25218-2
2. Dalgaard, Peter (2008), Введение в статистику с R (Второе издание), Springer, ISBN 978-0387790534
3. Saegusa, Takumi; Di, Chongzhi; Chen, Ying Qing (сентябрь 2014 г.). «Проверка гипотез для расширенной модели Кокса с коэффициентами, изменяющимися во времени». Biometrics . 70 (3): 619–628. doi :10.1111/biom.12185. ISSN  0006-341X. PMC 4247822 . 
4. Сигал, Марк Роберт (1988). «Регрессионные деревья для цензурированных данных». Биометрия . 44 (1): 35–47. doi :10.2307/2531894. JSTOR  2531894. S2CID  60974957.
5. Лебланк, Майкл; Кроули, Джон (1993). «Деревья выживания по доброте разделения». Журнал Американской статистической ассоциации . 88 (422): 457–467. doi :10.1080/01621459.1993.10476296. ISSN  0162-1459.
6. Ритчард, Гилберт; Габадинью, Алексис; Мюллер, Николас С.; Штудер, Маттиас (2008). «Истории событий в горнодобывающей промышленности: перспектива социальной науки». Международный журнал по интеллектуальному анализу данных, моделированию и управлению . 1 (1): 68. doi :10.1504/IJDMMM.2008.022538. ISSN  1759-1163.
7. Ishwaran, Hemant; Kogalur, Udaya B.; Blackstone, Eugene H.; Lauer, Michael S. (2008-09-01). "Случайные леса выживания". Annals of Applied Statistics . 2 (3). arXiv : 0811.1645 . doi : 10.1214/08-AOAS169 . ISSN  1932-6157. S2CID  2003897.
8. Therneau, Terry J.; Atkinson, Elizabeth J. "rpart: Recursive Partitioning and Regression Trees". CRAN . Получено 12 ноября 2021 г.
9. Аткинсон, Элизабет Дж.; Терно, Терри Дж. (1997). Введение в рекурсивное разбиение с использованием процедур RPART. Mayo Foundation.
10. Ишваран, Хемант; Когалур, Удайя Б. "randomForestSRC: Быстрые унифицированные случайные леса для выживания, регрессии и классификации (RF-SRC)". CRAN . Получено 12 ноября 2021 г.
11. Сингх, Джаред; Кацман, Л. (2018). «DeepSurv: персонализированная система рекомендаций по лечению с использованием глубокой нейронной сети пропорциональных рисков Кокса». Методология медицинских исследований BMC .
12. Нагпал, Чираг (2021). «Глубокие машины выживания: полностью параметрическая регрессия выживания и репрезентативное обучение для цензурированных данных с конкурирующими рисками». IEEE Journal of Biomedical and Health Informatics . 25 (8): 3163–3175. arXiv : 2003.01176 . doi : 10.1109/JBHI.2021.3052441. PMID  33460387. S2CID  211817982.
13. Нагпал, Чираг (2021). «Глубокие смеси Кокса для регрессии выживания». Конференция по машинному обучению для здравоохранения . arXiv : 2101.06536 .
14. Дарити, Уильям А. младший, ред. (2008). «Цензура, левая и правая». Международная энциклопедия социальных наук . Том 1 (2-е изд.). Macmillan. С. 473–474 . Получено 6 ноября 2016 г.
15. Ричардс, С. Дж. (2012). «Справочник параметрических моделей выживания для актуарного использования». Scandinavian Actuarial Journal . 2012 (4): 233–257. doi :10.1080/03461238.2010.506688. S2CID  119577304.
16. Сингх, Р.; Мукхопадхай, К. (2011). «Анализ выживаемости в клинических испытаниях: основы и области, которые необходимо знать». Perspect Clin Res . 2 (4): 145–148. doi : 10.4103/2229-3485.86872 . PMC 3227332. PMID  22145125 . 
17. Suresh, K., Severn, C. & Ghosh, D. Модели прогнозирования выживания: введение в дискретное моделирование. BMC Med Res Methodol 22, 207 (2022). https://doi.org/10.1186/s12874-022-01679-6 , https://bmcmedresmethodol.biomedcentral.com/articles/10.1186/s12874-022-01679-6
18. Эмпирическое правдоподобие в анализе выживания, Ган Ли (США), Рунзе Ли (США) и Май Чжоу (США), Современный многомерный анализ и планирование экспериментов. Март 2005 г., 337-349, https://www.ms.uky.edu/~mai/research/llz.pdf
19. Эмпирическая функция распределения с произвольно сгруппированными, цензурированными и усеченными данными, Брюс В. Тернбулл, Журнал Королевского статистического общества. Серия B (Методическая) Том 38, № 3 (1976), стр. 290-295 (6 страниц), https://apps.dtic.mil/sti/tr/pdf/ADA030940.pdf
20. Правильные правила подсчета очков для анализа выживания, Хироки Янагисава, https://arxiv.org/abs/2305.00621v3
21. Клейнбаум, Дэвид Г.; Клейн, Митчел (2012), Анализ выживания: Самостоятельное обучение (третье изд.), Springer, ISBN 978-1441966452
22. Бростром, Йоран (2012), Анализ истории событий с помощью R (первое издание), Chapman & Hall/CRC, ISBN 978-1439831649
23. Tableman, Mara; Kim, Jong Sung (2003), Анализ выживания с использованием S (первое издание), Chapman and Hall/CRC, ISBN 978-1584884088
24. Степанова, Мария; Томас, Лин (2002-04-01). «Методы анализа выживаемости для данных по персональным кредитам». Исследование операций . 50 (2): 277–289. doi :10.1287/opre.50.2.277.426. ISSN  0030-364X.
25. Гленнон, Деннис; Нигро, Питер (2005). «Измерение риска дефолта по кредитам для малого бизнеса: подход к анализу выживаемости». Журнал «Деньги, кредит и банковское дело» . 37 (5): 923–947. doi :10.1353/mcb.2005.0051. ISSN  0022-2879. JSTOR  3839153. S2CID  154615623.
26. Кеннеди, Эдвард Х.; Ху, Чэнь; О'Брайен, Барбара; Гросс, Сэмюэл Р. (2014-05-20). «Уровень ложного осуждения обвиняемых по уголовным делам, приговоренных к смертной казни». Труды Национальной академии наук . 111 (20): 7230–7235. Bibcode : 2014PNAS..111.7230G. doi : 10.1073/pnas.1306417111 . ISSN  0027-8424. PMC 4034186. PMID 24778209  . 
27. de Cos Juez, FJ; García Nieto, PJ; Martínez Torres, J.; Taboada Castro, J. (2010-10-01). "Анализ сроков изготовления металлических компонентов в аэрокосмической промышленности с помощью модели поддерживаемых векторов". Математическое и компьютерное моделирование . Математические модели в медицине, бизнесе и инжиниринге 2009. 52 (7): 1177–1184. doi : 10.1016/j.mcm.2010.03.017 . ISSN  0895-7177.
28. Спивак, Эндрю Л.; Дамфаус, Келли Р. (2006). «Кто возвращается в тюрьму? Анализ выживаемости рецидивистов среди взрослых правонарушителей, освобожденных в Оклахоме, 1985 – 2004». Исследования и политика в области правосудия . 8 (2): 57–88. doi :10.3818/jrp.8.2.2006.57. ISSN  1525-1071. S2CID  144566819.
29. Поллок, Кеннет Х.; Винтерстейн, Скотт Р.; Банк, Кристин М.; Кертис, Пол Д. (1989). «Анализ выживания в телеметрических исследованиях: пошаговый план входа». Журнал управления дикой природой . 53 (1): 7–15. doi :10.2307/3801296. ISSN  0022-541X. JSTOR  3801296.
30. Салех, Джозеф Хомер (2019-12-23). ​​«Статистический анализ надежности для самой опасной профессии: римский император». Palgrave Communications . 5 (1): 1–7. doi : 10.1057/s41599-019-0366-y . ISSN  2055-1045.
31. Kreer, Markus; Kizilersu, Ayse; Thomas, Anthony W. (2022). «Цензурированный алгоритм максимизации ожиданий для смесей: применение к межторговым временам ожидания». Physica A: Статистическая механика и ее приложения . 587 (1): 126456. Bibcode : 2022PhyA..58726456K. doi : 10.1016/j.physa.2021.126456. ISSN  0378-4371. S2CID  244198364.

Дальнейшее чтение

• Коллетт, Дэвид (2003). Моделирование данных о выживании в медицинских исследованиях (второе издание). Бока-Ратон: Chapman & Hall/CRC. ISBN 1584883251.
• Эландт-Джонсон, Регина; Джонсон, Норман (1999). Модели выживания и анализ данных . Нью-Йорк: John Wiley & Sons. ISBN 0471349925.
• Калбфляйш, доктор медицинских наук; Прентис, Росс Л. (2002). Статистический анализ данных о времени отказа . Нью-Йорк: Джон Уайли и сыновья. ISBN 047136357X.
• Лоулесс, Джеральд Ф. (2003). Статистические модели и методы для данных о продолжительности жизни (2-е изд.). Хобокен: John Wiley and Sons. ISBN 0471372153.
• Раусанд, М.; Хойланд, А. (2004). Теория надежности систем: модели, статистические методы и приложения . Хобокен: John Wiley & Sons. ISBN 047147133X.

Внешние ссылки

• Терно, Терри. "Пакет для анализа выживания в S". Архивировано из оригинала 2006-09-07.через страницу доктора Терно на сайте клиники Майо
• «Справочник по инженерной статистике». NIST/SEMATEK.
• SOCR , апплет анализа выживания и интерактивное обучающее занятие.
• Анализ времени выживания/отказа @ Статистика ' Учебник Страница
• Анализ выживаемости в R
• Lifelines, пакет Python для анализа выживания
• Анализ выживаемости в библиотеке NAG Fortran