
Трисекция угла — классическая задача построения с помощью циркуля и линейки в древнегреческой математике . Она касается построения угла, равного одной трети данного произвольного угла, с использованием только двух инструментов: неразмеченной линейки и циркуля .
В 1837 году Пьер Ванцель доказал, что задача, как она сформулирована, не может быть решена для произвольных углов. Однако некоторые специальные углы могут быть трисектированы: например, трисекция прямого угла тривиальна .
Можно трисекцию произвольного угла, используя инструменты, отличные от линейки и циркуля. Например, построение невзиса , также известное древним грекам, включает одновременное скольжение и вращение отмеченной линейки, чего нельзя было достичь с помощью оригинальных инструментов. Другие методы были разработаны математиками на протяжении столетий.
Поскольку она определяется простыми терминами, но сложна для доказательства неразрешимости, проблема трисекции угла часто становится предметом псевдоматематических попыток решения со стороны наивных энтузиастов. Эти «решения» часто включают ошибочные интерпретации правил или просто неверны. [1]
Используя только неразмеченную линейку и циркуль, греческие математики нашли способы разделить линию на произвольный набор равных отрезков, провести параллельные линии, разделить углы пополам , построить множество многоугольников и построить квадраты, площадь которых равна или вдвое больше площади заданного многоугольника.
Три проблемы оказались неуловимыми, а именно: трисекция угла, удвоение куба и квадратура круга . Задача трисекции угла звучит так:
Постройте угол , равный одной трети заданного произвольного угла (или разделите его на три равных угла), используя всего два инструмента:


Пьер Ванцель опубликовал доказательство невозможности классической трисекции произвольного угла в 1837 году. [2] Доказательство Ванцеля, перефразированное в современной терминологии, использует концепцию расширений поля , тему, которая теперь обычно объединяется с теорией Галуа . Однако Ванцель опубликовал эти результаты раньше Эвариста Галуа (чья работа, написанная в 1830 году, была опубликована только в 1846 году) и не использовал концепции, введенные Галуа. [3]
Задача построения угла заданной меры θ эквивалентна построению двух отрезков, отношение длин которых равно cos θ . От решения одной из этих двух задач можно перейти к решению другой с помощью построения циркулем и линейкой. Формула тройного угла дает выражение, связывающее косинусы исходного угла и его трисекции: cos θ = 4 cos 3 θ/3 − 3 cos θ/3 .
Отсюда следует, что при заданном отрезке, длина которого определена как единичная, задача трисекции угла эквивалентна построению отрезка, длина которого является корнем кубического многочлена . Эта эквивалентность сводит исходную геометрическую задачу к чисто алгебраической задаче.
Каждое рациональное число конструируемо. Каждое иррациональное число , конструируемое за один шаг из некоторых заданных чисел, является корнем многочлена степени 2 с коэффициентами в поле, порожденном этими числами. Следовательно, любое число, конструируемое последовательностью шагов, является корнем минимального многочлена, степень которого является степенью двойки . Угол π/3 радианы (60 градусов , пишется 60°) конструируемы . Приведенное ниже рассуждение показывает, что невозможно построить угол в 20°. Это означает, что угол в 60° не может быть разделен на три части, и, таким образом, произвольный угол не может быть разделен на три части.
Обозначим множество рациональных чисел через Q. Если бы 60° можно было разделить на три части, степень минимального многочлена cos 20° над Q была бы степенью двойки. Теперь пусть x = cos 20° . Обратите внимание, что cos 60° = cos π/3 = 1/2 . Тогда по формуле тройного угла, cos π/3 = 4 x 3 − 3 x и поэтому 4 x 3 − 3 x = 1/2 . Таким образом, 8 x 3 − 6 x − 1 = 0. Определим p ( t ) как многочлен p ( t ) = 8 t 3 − 6 t − 1 .
Так как x = cos 20° является корнем p ( t ) , минимальный многочлен для cos 20° является множителем p ( t ) . Так как p ( t ) имеет степень 3, если он редуцируется с помощью Q , то он имеет рациональный корень . По теореме о рациональном корне этот корень должен быть ±1, ± 1/2 , ± 1/4 или ± 1/8 , но ни один из них не является корнем. Следовательно, p ( t ) неприводимнад Q , а минимальный многочлен для cos 20° имеет степень 3 .
Таким образом, угол величиной 60° не может быть разделен на три равные части.
Однако некоторые углы можно трисектировать. Например, для любого конструируемого угла θ угол меры 3 θ можно тривиально трисектировать, игнорируя заданный угол и напрямую строя угол меры θ . Существуют углы, которые не конструируемы, но трисектируемы (несмотря на то, что сам угол в одну треть не конструируем). Например, 3π/7 такой угол: пять углов меры 3π/7 объединить, чтобы получить угол измерения 15π/7 , что представляет собой полный круг плюс желаемое π/7 .
Для положительного целого числа N угол меры 2π/Н является трисекущим тогда и только тогда, когда 3 не делит N . [4] [5] Напротив, 2π/Н конструируемотогда и только тогда, когда N является степенью числа 2 или произведением степени числа 2 на произведение одного или нескольких различных простых чисел Ферма .
Снова обозначим множество рациональных чисел через Q.
Теорема : Угол меры θ может быть разделен на три части тогда и только тогда, когда q ( t ) = 4 t 3 − 3 t − cos( θ ) приводим над расширением поля Q (cos( θ )) .
Доказательство представляет собой относительно простое обобщение приведенного выше доказательства того, что угол в 60° не является трисекторным. [6]
Для любого ненулевого целого числа N угол величиной 2π ⁄ N радиан можно разделить на n равных частей с помощью линейки и циркуля тогда и только тогда, когда n является либо степенью 2 , либо степенью 2, умноженной на произведение одного или нескольких различных простых чисел Ферма, ни одно из которых не делит N. В случае трисекции ( n = 3 , что является простым числом Ферма) это условие становится вышеупомянутым требованием, чтобы N не делилось на 3. [5]
Общую задачу трисекции угла можно решить, используя дополнительные инструменты и, таким образом, выходя за рамки изначальных греческих рамок циркуля и линейки.
Было предложено много неправильных методов трисекции общего угла. Некоторые из этих методов дают разумные приближения; другие (некоторые из которых упомянуты ниже) включают инструменты, не разрешенные в классической задаче. Математик Андервуд Дадли подробно описал некоторые из этих неудачных попыток в своей книге «Трисекторы» . [1]
Трисекция может быть аппроксимирована повторением метода циркуля и линейки для деления угла пополам. Геометрическая прогрессия 1/3 = 1/4 + 1/16 + 1/64 + 1/256 + ⋯ или 1/3 = 1/2 − 1/4 + 1/8 − 1/16 + ⋯ может быть использовано в качестве основы для деления пополам. Приближение любой степени точности может быть получено за конечное число шагов. [7]
Трисекция, как и многие конструкции, невозможные с помощью линейки и циркуля, может быть легко выполнена с помощью операций складывания бумаги, или оригами . Аксиомы Хузиты (типы операций складывания) позволяют строить кубические расширения (кубические корни) заданных длин, тогда как линейка и циркуль позволяют строить только квадратные расширения (квадратные корни).

Существует ряд простых соединений , которые можно использовать для создания инструмента для трисекции углов, включая трисектор Кемпе и веер Сильвестра или изоклиностат. [8]
В 1932 году Людвиг Бибербах опубликовал в Journal für die reine und angewandte Mathematik свою работу Zur Lehre von den kubischen Konstruktionen . [9] Там он утверждает (вольный перевод):
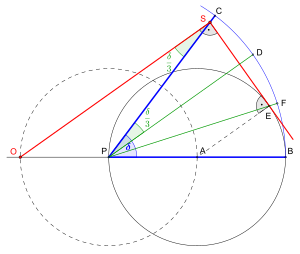
Построение начинается с рисования окружности, проходящей через вершину P угла, который нужно разделить на три части, с центром в точке A на ребре этого угла и имеющей точку B в качестве своей второй точки пересечения с ребром. Окружность с центром в точке P и того же радиуса пересекает линию, поддерживающую ребро в точках A и O.
Теперь прямоугольная линейка размещена на чертеже следующим образом: одна сторона ее прямого угла проходит через O ; вершина ее прямого угла расположена в точке S на прямой PC таким образом, что вторая сторона линейки касается в точке E окружности с центром в точке A. Отсюда следует, что исходный угол делится на три части прямой PE , а линия PD перпендикулярна SE и проходит через P. Эту линию можно провести либо снова с помощью прямоугольной линейки, либо с помощью традиционной линейки и построения циркуля . С помощью аналогичного построения можно улучшить местоположение точки E , используя то, что она является пересечением прямой SE и ее перпендикуляра , проходящего через A.
Доказательство: Нужно доказать равенства углов и Три прямые OS , PD и AE параллельны. Поскольку отрезки OP и PA равны, эти три параллельные прямые ограничивают два равных отрезка на каждой другой секущей линии, и, в частности, на их общем перпендикуляре SE . Таким образом, SD ' = D ' E , где D' - пересечение прямых PD и SE . Отсюда следует, что прямоугольные треугольники PD ' S и PD ' E равны, и, таким образом, первое искомое равенство. С другой стороны, треугольник PAE равнобедренный , поскольку все радиусы окружности равны; это подразумевает, что Также имеем, поскольку эти два угла являются накрест лежащими углами секущей к двум параллельным прямым. Это доказывает второе искомое равенство, а значит, и правильность построения.
Существуют определенные кривые, называемые трисектрисами , которые, если их нарисовать на плоскости другими методами, можно использовать для трисектрисы произвольных углов. [10] Примерами служат трисектрисы Колина Маклорена , заданные в декартовых координатах неявным уравнением
и спираль Архимеда . Спираль может быть фактически использована для деления угла на любое количество равных частей. Архимед описал, как трисектировать угол с помощью спирали Архимеда в «О спиралях» около 225 г. до н. э.

Другой способ трисекции произвольного угла на «маленький» шаг за пределами греческой системы — с помощью линейки с двумя отметками на заданном расстоянии друг от друга. Следующая конструкция изначально принадлежит Архимеду и называется конструкцией Нейзиса , то есть, которая использует инструменты, отличные от неотмеченной линейки. На схемах, которые мы используем, эта конструкция показана для острого угла, но она действительно работает для любого угла до 180 градусов.
Для этого необходимы три факта из геометрии (справа):
Пусть l будет горизонтальной линией на соседней диаграмме. Угол a (слева от точки B ) является предметом трисекции. Сначала на луче угла , на расстоянии одной единицы от B , строится точка A . Строится окружность радиуса AB . Затем в игру вступает разметка линейки: одна отметка линейки помещается в A , а другая в B . Удерживая линейку (но не отметку) касающейся A , линейку скользят и вращают до тех пор, пока одна отметка не окажется на окружности, а другая — на линии l . Отметка на окружности обозначена C , а отметка на линии обозначена D . Это гарантирует, что CD = AB . Радиус BC нарисован, чтобы было очевидно, что отрезки AB , BC и CD имеют одинаковую длину. Теперь треугольники ABC и BCD являются равнобедренными , поэтому (согласно факту 3 выше) каждый из них имеет два равных угла.
Гипотеза : если AD — прямая линия, а AB , BC и CD имеют одинаковую длину,
Вывод : угол b = а/3 .
и теорема доказана.
Опять же, эта конструкция вышла за рамки разрешенных конструкций , используя размеченную линейку.
Томас Хатчесон опубликовал статью в Mathematics Teacher [11] , в которой использовал нить вместо циркуля и линейки. Струна может использоваться как линейка (растягивая ее) или циркуль (фиксируя одну точку и определяя другую), но также может быть обернута вокруг цилиндра, что является ключом к решению Хатчесона.
Хатчесон построил цилиндр из угла, который нужно было разделить на три части, проведя дугу через угол, завершив ее до окружности, и построив из этой окружности цилиндр, в который был вписан, скажем, равносторонний треугольник (угол в 360 градусов, разделенный на три части). Затем это было «отображено» на угол, который нужно было разделить на три части, с помощью простого доказательства подобия треугольников.
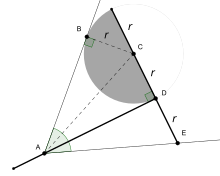
« Томагавк » — это геометрическая фигура, состоящая из полукруга и двух ортогональных отрезков, так что длина более короткого отрезка равна радиусу окружности. Трисекция выполняется путем опирания конца более короткого отрезка томагавка на один луч, края круга — на другой, так что «ручка» (более длинный отрезок) пересекает вершину угла; линия трисекции проходит между вершиной и центром полукруга.
Хотя томагавк можно построить с помощью циркуля и линейки, в общем случае невозможно построить томагавк в любом желаемом положении. Таким образом, приведенная выше конструкция не противоречит нетрисектабельности углов с помощью только линейки и циркуля.
Так как томагавк можно использовать в качестве угольника , его также можно использовать для измерения углов трисекции методом, описанным в § С помощью прямоугольной треугольной линейки.
Томагавк производит тот же геометрический эффект, что и метод складывания бумаги: расстояние между центром круга и кончиком более короткого сегмента в два раза больше расстояния радиуса, который гарантированно касается угла. Это также эквивалентно использованию архитектурной L-линейки ( плотничного угольника ).
Угол можно разделить на три части с помощью устройства, которое по сути является четырехзубчатой версией циркуля, со связями между зубцами, предназначенными для поддержания равенства трех углов между соседними зубцами. [12]

Кубическое уравнение с действительными коэффициентами можно решить геометрически с помощью циркуля, линейки и трисектора углов тогда и только тогда, когда оно имеет три действительных корня . [13] : Теор. 1
Правильный многоугольник с n сторонами может быть построен с помощью линейки, циркуля и трисектора углов тогда и только тогда, когда r, s, k ≥ 0 и где p i являются различными простыми числами, большими 3, вида (т. е. простыми числами Пьерпонта, большими 3). [13] : Теор. 2
См. также Отзыв об этой статье в т. 93, март 2009 г., стр. 156.