Сравнение правил голосования

Сравнительная политология избирательных систем

В этой статье обсуждаются методы и результаты сравнения различных избирательных систем . Существует два основных способа сравнения систем голосования:

1. Показатели удовлетворенности избирателей, полученные с помощью моделирования или опроса.
2. Соблюдение логических критериев.

Оценка по метрикам

Модели избирательного процесса

Методы голосования можно оценить, измерив их точность в случайных смоделированных выборах, стремящихся к верности свойствам выборов в реальной жизни. Первая такая оценка была проведена Чемберлином и Коэном в 1978 году, которые измерили частоту, с которой определенные некондорсеанские системы выбирали победителей Кондорсе. ^[1]

Модель жюри Кондорсе

Маркиз де Кондорсе рассматривал выборы как аналог голосования присяжных, где каждый член выражает независимое суждение о качестве кандидатов. Кандидаты различаются по своим объективным достоинствам, но избиратели имеют несовершенную информацию об относительных достоинствах кандидатов. Такие модели присяжных иногда называют моделями валентности . Кондорсе и его современник Лаплас продемонстрировали, что в такой модели теория голосования может быть сведена к вероятности путем нахождения ожидаемого качества каждого кандидата. ^[2]

Модель присяжных подразумевает несколько естественных концепций точности для систем голосования в рамках различных моделей:

1. Если оценки избирателей имеют ошибки, следующие нормальному распределению , идеальной процедурой является балльное голосование .
2. Если доступна только информация о рейтинге, а избирателей намного больше, чем кандидатов, любой метод Кондорсе приведет к единому победителю Кондорсе, который будет иметь наибольшую вероятность оказаться лучшим кандидатом. ^[3]

Однако модель Кондорсе основана на чрезвычайно сильном предположении о независимых ошибках , т. е. избиратели не будут систематически предвзяты в пользу той или иной группы кандидатов. Обычно это нереалистично: избиратели склонны общаться друг с другом, формировать партии или политические идеологии и заниматься другим поведением, которое может привести к коррелированным ошибкам .

Пространственная модель Блэка

Дункан Блэк предложил одномерную пространственную модель голосования в 1948 году, рассматривая выборы как идеологически обусловленные. ^[4] Его идеи позже были расширены Энтони Даунсом. ^[5] Мнения избирателей рассматриваются как позиции в пространстве одного или нескольких измерений; кандидаты имеют позиции в том же пространстве; и избиратели выбирают кандидатов в порядке близости (измеряемой с помощью евклидова расстояния или какой-либо другой метрики).

Пространственные модели подразумевают иное понятие заслуг для систем голосования: чем более приемлемым может быть победивший кандидат в качестве параметра местоположения для распределения избирателей, тем лучше система. Политический спектр — это одномерная пространственная модель.

Нейтральные модели

Нейтральные модели голосования пытаются минимизировать количество параметров и, как пример принципа « ничего в рукаве» . Наиболее распространенной такой моделью является модель беспристрастной анонимной культуры (или модель Дирихле ). Эти модели предполагают, что избиратели назначают каждому кандидату полезность совершенно случайным образом (из равномерного распределения ).

Сравнение моделей

Тайдман и Плассманн провели исследование, которое показало, что двумерная пространственная модель дала разумное соответствие сокращению на 3 кандидата большого набора избирательных рейтингов. Модели жюри, нейтральные модели и одномерные пространственные модели были неадекватны. ^[6] Они рассмотрели циклы Кондорсе в предпочтениях избирателей (примером которых является предпочтение A перед B большинством избирателей, B перед C и C перед A) и обнаружили, что их количество соответствовало эффектам малой выборки, заключив, что «циклы голосования будут происходить очень редко, если вообще будут, на выборах с большим количеством избирателей». Соответствие размера выборки ранее изучал Гордон Таллок , который наглядно утверждал, что, хотя конечные электораты будут склонны к циклам, область, в которой кандидаты могут вызывать цикличность, сужается по мере увеличения числа избирателей. ^[7]

Утилитарные модели

Утилитарная модель рассматривает избирателей как ранжирующих кандидатов в порядке полезности. Законным победителем в этой модели является кандидат, который максимизирует общую общественную полезность. Утилитарная модель отличается от пространственной модели несколькими важными способами:

• Для этого необходимо дополнительное предположение о том, что избиратели мотивированы исключительно осознанным личным интересом, без какой-либо идеологической окраски в своих предпочтениях.
• Для этого необходимо заменить метрику расстояния пространственной модели на точную меру полезности.
• Следовательно, метрика должна будет различаться между избирателями. Часто случается, что одна группа избирателей будет сильно затронута выбором между двумя кандидатами, в то время как другая группа не будет иметь больших ставок; тогда метрика должна будет быть крайне асимметричной.

Из последнего свойства следует, что ни одна система голосования, которая дает равное влияние всем избирателям, не сможет достичь максимальной общественной полезности. Крайние случаи конфликта между требованиями утилитаризма и демократии называются « тиранией большинства ». См. комментарии Ласлиера, Мерлина и Нурми в статье Ласлиера. ^[8]

Джеймс Милль , по-видимому, был первым, кто заявил о существовании априорной связи между демократией и утилитаризмом – см. статью в Стэнфордской энциклопедии. ^[9]

Сравнения в рамках модели присяжных

Предположим, что i-  ^й  кандидат на выборах имеет заслуги x _i (мы можем предположить, что x _i  ~  N  (0, σ ² ) ^[10] ), и что уровень одобрения избирателем j  кандидата i может быть записан как x _i  + ε _ij (мы будем предполагать, что ε _ij являются iid. N  (0,τ ² )). Мы предполагаем, что избиратель ранжирует кандидатов в порядке убывания одобрения. Мы можем интерпретировать ε _ij как ошибку в оценке избирателем j  кандидата i и рассматривать метод голосования как имеющий задачу нахождения кандидата с наибольшими заслугами.

Каждый избиратель оценит лучшего из двух кандидатов выше, чем менее хорошего с определенной вероятностью p (которая в рамках описанной здесь нормальной модели равна , что можно подтвердить с помощью стандартной формулы для гауссовых интегралов по квадранту ^{[ требуется ссылка ]} ). Теорема Кондорсе о жюри показывает, что пока p  >  1 ⁄ 2 , большинство голосов жюри будет лучшим руководством для оценки относительных достоинств двух кандидатов, чем мнение любого отдельного члена. ${\displaystyle {\tfrac {1}{2}}\!+\!{\tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {\sigma }{\tau }}}$

Пейтон Янг показал, что к голосам между произвольным числом кандидатов применимы еще три свойства, что позволяет предположить, что Кондорсе знал о первом и третьем из них. ^[11]

• Если p близко к 1 ⁄ 2 , то победителем Борда является оценка максимального правдоподобия наилучшего кандидата.
• если p близко к 1, то победителем Minimax является оценка максимального правдоподобия наилучшего кандидата.
• Для любого p рейтинг Кемени-Янга является оценкой максимального правдоподобия истинного порядка заслуг.

Роберт Ф. Бордли построил «утилитарную» модель, которая является небольшим вариантом модели жюри Кондорсе. ^[12] Он рассматривал задачу метода голосования как нахождение кандидата, который имеет наибольшее общее одобрение электората, т. е. самую высокую сумму уровней одобрения отдельных избирателей. Эта модель имеет смысл даже при σ ²  = 0, в этом случае p принимает значение, где n — число избирателей. Он провел оценку в рамках этой модели, обнаружив, как и ожидалось, что подсчет Борда был наиболее точным. ${\displaystyle {\tfrac {1}{2}}\!+\!{\tfrac {1}{\pi }}{\textrm {tan}}^{-1}{\tfrac {1}{n-1}}}$

Имитация выборов в рамках пространственных моделей

Имитация выборов в двух измерениях

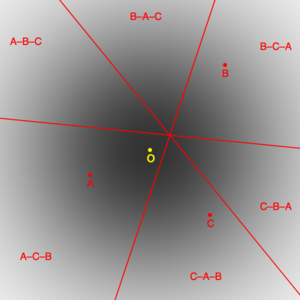
Моделируемые выборы могут быть построены из распределения избирателей в подходящем пространстве. На иллюстрации показаны избиратели, удовлетворяющие двумерному гауссовскому распределению с центром в точке O. Есть 3 случайно сгенерированных кандидата, A, B и C. Пространство разделено на 6 сегментов тремя линиями, причем избиратели в каждом сегменте имеют одинаковые предпочтения кандидатов. Доля избирателей, упорядочивающих кандидатов каким-либо образом, определяется интегралом распределения избирателей по соответствующему сегменту.

Пропорции, соответствующие 6 возможным порядкам кандидатов, определяют результаты, полученные различными системами голосования. Те, которые выбирают лучшего кандидата, т. е. кандидата, ближайшего к O (в данном случае это A), считаются давшими правильный результат, а те, которые выбирают кого-то другого, показали ошибку. Рассматривая результаты для большого количества случайно сгенерированных кандидатов, можно измерить эмпирические свойства систем голосования.

Протокол оценки, описанный здесь, смоделирован на основе протокола, описанного Тайдманом и Плассманном. ^[6] Оценки такого типа наиболее распространены для избирательных систем с одним победителем. Рейтинговые системы голосования наиболее естественно вписываются в рамки, но другие типы голосования (такие как FPTP и голосование одобрения ) могут быть адаптированы с меньшими или большими усилиями.

Протокол оценки можно варьировать несколькими способами:

• Число избирателей можно сделать конечным и разнообразным по размеру. На практике это почти всегда делается в многомерных моделях, при этом избиратели выбираются из своего распределения, а результаты для больших электоратов используются для демонстрации ограничивающего поведения.
• Количество кандидатов может варьироваться.
• Распределение избирателей может быть различным; например, можно исследовать эффект асимметричных распределений. Незначительное отклонение от нормальности влечет за собой случайные эффекты выборки, когда число избирателей конечно. Более систематические отклонения (по-видимому, принимающие форму модели гауссовой смеси ) были исследованы Джеймсоном Куинном в 2017 году. ^[13]

Оценка точности

Одно из основных применений оценок — сравнение точности систем голосования, когда избиратели голосуют искренне. Если бесконечное число избирателей удовлетворяет гауссовскому распределению, то законным победителем выборов можно считать кандидата, наиболее близкого к среднему/медиане, а точность метода можно определить по доле выборов, на которых избран законный победитель. Теорема о медианном избирателе гарантирует, что все системы Кондорсе дадут 100% точность (и то же самое относится к методу Кумбса ^[14] ).

Оценки, опубликованные в исследовательских работах, используют многомерные гауссианы, что затрудняет численные вычисления. ^{[1] [15] [16] [17]} Число избирателей сохраняется конечным, а число кандидатов обязательно небольшим.

B выбывает в первом раунде по правилам IRV

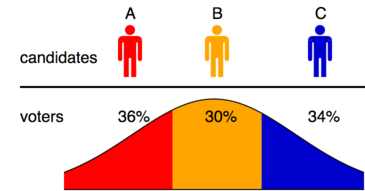
Вычисление гораздо более прямолинейно в одномерном случае, что допускает бесконечное число избирателей и произвольное число m кандидатов. Результаты для этого простого случая показаны в первой таблице, которая напрямую сопоставима с таблицей 5 (1000 избирателей, средняя дисперсия) цитируемой статьи Чемберлина и Коэна. Кандидаты были выбраны случайным образом из распределения избирателей, и один метод Кондорсе ( Минимакс ) был включен в испытания для подтверждения.

Относительно плохие результаты альтернативного голосования (IRV) объясняются хорошо известным и распространенным источником ошибок, проиллюстрированным диаграммой, в которой выборы удовлетворяют одномерной пространственной модели, а законный победитель B будет устранен в первом туре. Подобная проблема существует во всех измерениях.

Альтернативной мерой точности является среднее расстояние избирателей от победителя (где меньше означает лучше). Это вряд ли изменит рейтинг методов голосования, но является предпочтительным для людей, которые интерпретируют расстояние как бесполезность. Вторая таблица показывает среднее расстояние (в стандартных отклонениях) минус (что является средним расстоянием переменной от центра стандартного гауссовского распределения) для 10 кандидатов в рамках той же модели. ${\displaystyle {\sqrt {\tfrac {2}{\pi }}}}$

Оценка устойчивости к тактическому голосованию

Джеймс Грин-Армитедж и др. опубликовали исследование, в котором они оценили уязвимость нескольких систем голосования к манипуляциям со стороны избирателей. ^[18] Они мало говорят о том, как они адаптировали свою оценку для этой цели, упоминая лишь, что это «требует творческого программирования». Более ранняя статья первого автора дает немного больше подробностей. ^[19]

Число кандидатов в их моделируемых выборах было ограничено тремя. Это устраняет различие между некоторыми системами; например, метод Блэка и метод Дасгупты-Маскина эквивалентны при трех кандидатах.

Выводы из исследования трудно обобщить, но подсчет Борда показал плохие результаты; Minimax был несколько уязвим; а IRV был очень устойчив. Авторы показали, что ограничение любого метода выборами без победителя по Кондорсе (выбор победителя по Кондорсе, когда он был) никогда не увеличит его восприимчивость к тактическому голосованию . Они сообщили, что система «Кондорсе-Хара», которая использует IRV в качестве дополнительного фактора для выборов, не разрешенных критерием Кондорсе, была столь же устойчива к тактическому голосованию, как и IRV сам по себе, и более точна. Метод Кондорсе-Хара эквивалентен методу Коупленда с дополнительным фактором IRV на выборах с 3 кандидатами.

Оценка влияния распределения кандидатов

Некоторые системы, и в частности подсчет Борда, уязвимы, когда распределение кандидатов смещено относительно распределения избирателей. Прилагаемая таблица показывает точность подсчета Борда (в процентах), когда бесконечная популяция избирателей удовлетворяет одномерному гауссовскому распределению, а m кандидатов взяты из аналогичного распределения, смещенного на x стандартных распределений. Красным цветом обозначены цифры, которые хуже случайных. Напомним, что все методы Кондорсе дают 100% точность для этой задачи. (И обратите внимание, что снижение точности при увеличении x не наблюдается, когда есть только 3 кандидата.)

Чувствительность к распределению кандидатов можно рассматривать как вопрос либо точности, либо сопротивления манипуляциям. Если кто-то ожидает, что в ходе событий кандидаты естественным образом будут происходить из того же распределения, что и избиратели, то любое смещение будет рассматриваться как попытка подрыва; но если кто-то думает, что факторы, определяющие жизнеспособность кандидатуры (например, финансовая поддержка), могут быть связаны с идеологической позицией, то он будет рассматривать это скорее с точки зрения точности.

Опубликованные оценки по-разному рассматривают распределение кандидатов. Некоторые просто предполагают, что кандидаты берутся из того же распределения, что и избиратели. ^{[16] [18]} Несколько более старых работ предполагают равные средние значения, но допускают, что распределение кандидатов может быть более или менее плотным, чем распределение избирателей. ^{[20] [1]} Статья Тидемана и Плассманна аппроксимирует связь между распределениями кандидатов и избирателей на основе эмпирических измерений. ^[15] Это менее реалистично, чем может показаться, поскольку не допускает корректировки распределения кандидатов для использования любой слабости в системе голосования. Статья Джеймса Грина-Армитеджа рассматривает распределение кандидатов как отдельную проблему, рассматривая его как форму манипуляции и измеряя эффекты стратегического входа и выхода. Неудивительно, что он считает подсчет Борда особенно уязвимым. ^[19]

Оценка других объектов недвижимости

• Как упоминалось ранее, Чемберлин и Коэн измерили частоту, с которой некоторые некондорсеанские системы выбирают победителей Кондорсе. В пространственной модели с равным распределением избирателей и кандидатов частоты составляют 99% ( Кумбс ), 86% (Борда), 60% (IRV) и 33% (FPTP). ^[1] Иногда это называют эффективностью Кондорсе .
• Дарлингтон измерил частоту, с которой метод Коупленда выдает уникального победителя на выборах без победителя по Кондорсе. Он обнаружил, что она составляет менее 50% для полей до 10 кандидатов. ^[17]

Экспериментальные метрики

Двое выборов с одними и теми же кандидатами

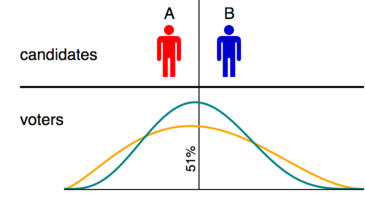
Задача системы голосования в рамках пространственной модели — определить кандидата, позиция которого наиболее точно отражает распределение мнений избирателей. Это равносильно выбору параметра местоположения для распределения из набора альтернатив, предлагаемых кандидатами. Параметры местоположения могут быть основаны на среднем значении, медиане или моде; но поскольку ранжированные бюллетени предпочтений предоставляют только порядковую информацию, медиана является единственной приемлемой статистикой.

Это можно увидеть на диаграмме, которая иллюстрирует двое смоделированных выборов с одними и теми же кандидатами, но разным распределением избирателей. В обоих случаях средняя точка между кандидатами — это 51-й процентиль распределения избирателей; следовательно, 51% избирателей предпочитают A, а 49% — B. Если мы считаем метод голосования правильным, если он выбирает кандидата, наиболее близкого к медиане популяции избирателей, то, поскольку медиана обязательно находится немного левее линии 51%, метод голосования будет считаться правильным, если он выбирает A в каждом случае.

Среднее значение распределения teal также немного левее линии 51%, но среднее значение распределения orange немного правее. Следовательно, если мы считаем метод голосования правильным, если он выбирает кандидата, наиболее близкого к среднему значению популяции избирателей, то метод не сможет получить полные баллы, если только он не выявит разных победителей из одних и тех же бюллетеней на двух выборах. Очевидно, что это припишет ложные ошибки методам голосования. Та же проблема возникнет для любой кардинальной меры местоположения; только медиана дает последовательные результаты.

Медиана не определена для многомерных распределений, но одномерная медиана имеет свойство, которое удобно обобщается. Медиана распределения — это позиция, среднее расстояние от которой до всех точек в пределах распределения наименьшее. Это определение обобщается до геометрической медианы в нескольких измерениях. Расстояние часто определяется как функция отрицательной полезности избирателя .

Если у нас есть набор кандидатов и популяция избирателей, то нет необходимости решать вычислительно сложную задачу нахождения геометрической медианы избирателей и затем определять кандидата, ближайшего к ней; вместо этого мы можем определить кандидата, чье среднее расстояние от избирателей минимизировано. Это метрика, которая обычно используется со времен Меррилла; ^[20] см. также Green-Armytage и Darlington. ^{[19] [16]}

Кандидата, наиболее близкого к геометрической медиане распределения избирателей, можно назвать «пространственным победителем».

Оценка по реальным выборам

Данные реальных выборов можно анализировать для сравнения эффектов различных систем, либо сравнивая между странами, либо применяя альтернативные избирательные системы к данным реальных выборов. Результаты выборов можно сравнивать с помощью индексов демократии , мер политической фрагментации , явки избирателей , ^{[21] [22]} политической эффективности и различных экономических и судебных показателей. Практические критерии оценки реальных выборов включают долю потерянных голосов , сложность подсчета голосов , пропорциональность и барьеры для входа новых политических движений. ^[23] Дополнительные возможности для сравнения реальных выборов возникают благодаря избирательным реформам .

Канадский пример такой возможности можно увидеть в городе Эдмонтон (Канада), который перешел от голосования по системе относительного большинства на всеобщих выборах в Альберте 1917 года к пятимандатному плюралистическому голосованию на всеобщих выборах в Альберте 1921 года , к пятимандатному единому передаваемому голосованию на всеобщих выборах в Альберте 1926 года , а затем снова к FPTP на всеобщих выборах в Альберте 1959 года . Одна партия заняла все места в Эдмонтоне в 1917, 1921 и 1959 годах. В рамках STV в 1926 году были избраны два консерватора, один либерал, один лейборист и один депутат Законодательного собрания от United Farmers.

Сравнение методов голосования с одним победителем

Логические критерии выборов с одним победителем

Традиционно достоинства различных избирательных систем аргументировались посредством ссылки на логические критерии. Они имеют форму правил вывода для избирательных решений, лицензирующих вывод, например, что «если E и E  ' являются выборами такими, что R  ( E , E  '), и если A является законным победителем E  , то A является законным победителем E  ' ».

Критерии результата (абсолютные)

Абсолютные критерии гласят, что если набор бюллетеней сформирован определенным образом, то определенный кандидат должен победить или не победить.

Критерии результата (относительные)

Это критерии, которые гласят, что если определенный кандидат побеждает в одних обстоятельствах, этот же кандидат должен (или не должен) победить в связанных обстоятельствах.

Критерии подсчета голосов

Это критерии, которые касаются процесса подсчета голосов и определения победителя.

Критерии стратегии

Это критерии, которые относятся к стимулу избирателя использовать определенные формы стратегии. Их также можно рассматривать как критерии относительного результата; однако, в отличие от критериев в этом разделе, эти критерии имеют прямое отношение к избирателям; тот факт, что метод соответствует этим критериям, может упростить процесс определения оптимального стратегического голоса.

Формат бюллетеня

Бюллетени в целом можно разделить на две категории: кардинальные и порядковые , где кардинальные бюллетени запрашивают индивидуальные меры поддержки для каждого кандидата, а порядковые бюллетени запрашивают относительные меры поддержки. Несколько методов не попадают четко в одну категорию, например, STAR, который просит избирателя дать независимые оценки для каждого кандидата, но использует как абсолютные, так и относительные оценки для определения победителя. Сравнение двух методов, основанных только на типе бюллетеня, в основном является вопросом предпочтений избирателя, если только тип бюллетеня не связан с одним из других математических критериев, перечисленных здесь.

Относительная сила

Критерий A "сильнее" B, если удовлетворение A подразумевает удовлетворение B. Например, критерий Кондорсе сильнее критерия большинства, поскольку все победители большинства являются победителями Кондорсе. Таким образом, любой метод голосования, удовлетворяющий критерию Кондорсе, должен удовлетворять критерию большинства.

Соответствие выбранным методам с одним победителем

В следующей таблице показано, каким из вышеперечисленных критериев соответствуют несколько методов с одним победителем. Не все критерии перечислены.

Практические факторы

Вышеизложенные опасения используются теоретиками общественного выбора для разработки систем, которые являются точными и устойчивыми к манипуляциям. Однако существуют также практические причины, по которым одна система может быть более социально приемлемой, чем другая, которые относятся к областям общественного выбора и политической науки . ^{[8] [16]} Важные практические соображения включают:

• Простота объяснения . Некоторые правила голосования трудно объяснить избирателям интуитивно понятным способом, что может подорвать доверие общественности к выборам. ^{[8] [ неудачная проверка ]} Например, хотя правило Шульце хорошо работает по многим из вышеперечисленных критериев, оно требует подробного объяснения путей обхода .
• Простота голосования . Различные виды бюллетеней могут быть более простыми для заполнения; например, исследования обычно показывают, что избиратели обычно считают рейтинговое голосование сложным и запутанным по сравнению с рейтинговым голосованием или голосованием по относительному числу избирателей .

Другие соображения включают барьеры для входа в политическую конкуренцию ^[28] и вероятность тупиковой ситуации в правительстве . ^[29]

Сравнение систем с несколькими победителями

Избирательные системы с несколькими победителями в лучшем случае стремятся создать собрания, репрезентативные в более широком смысле, чем те, которые принимают те же решения, которые принимались бы при голосовании с одним победителем. Они также могут быть путем к однопартийным зачисткам городских мест, если используется непропорциональная система, такая как голосование по плюралистическому блоку или голосование по билетам .

Метрики для оценки нескольких победителей

Оценка эффективности методов голосования с несколькими победителями требует других метрик, чем те, которые используются для систем с одним победителем. Было предложено следующее.

• Эффективность Комитета Кондорсе (CCE) измеряет вероятность того, что группа избранных победителей победит всех проигравших в парных гонках. ^[30]
• Индекс Галлахера и индекс Лусмора–Хэнби (LH) измеряют пропорциональность между долей мест и долей голосов партии. Галлахер обычно использует общие проценты голосов партии или голоса по сравнению с процентами мест для оценки пропорциональности, поэтому игнорирует наличие округов, если таковые имеются.
• Потери голосов измеряют долю электората, не представленную ни одним представителем.

Таблицы критериев

В следующей таблице показано, каким из вышеперечисленных критериев соответствуют несколько методов множественного выигрыша.

Смотрите также

• Рейтинговое голосование
• Теорема Эрроу о невозможности
• Количественная полезность и порядковая полезность
• Парадокс Кондорсе

Ссылки

1. Чемберлин, Джон Р.; Коэн, Майкл Д. (декабрь 1978 г.). «К применимой теории социального выбора: сравнение функций социального выбора при предположениях пространственной модели». American Political Science Review . 72 (4): 1341–1356. doi :10.2307/1954543. ISSN  0003-0554. JSTOR  1954543. S2CID  155928569.
2. МЬЯН де Карита, маркиз де Кондорсе. Его книга была опубликована в 1785 году. Название можно перевести как «Опыт о применении теории вероятностей к голосованию по мажоритарной системе».
3. О Кондорсе и Лапласе см. GG Szpiro, «Numbers Rule» (2010).
4. Блэк, Дункан (1948). «О рациональности группового принятия решений». Журнал политической экономии . 56 (1): 23–34. doi :10.1086/256633. ISSN  0022-3808. S2CID  153953456.
5. Энтони Даунс, « Экономическая теория демократии » (1957).
6. Tideman, T. Nicolaus; Plassmann, Florenz (2012), Felsenthal, Dan S.; Machover, Moshé (ред.), «Моделирование результатов голосования на реальных выборах», Electoral Systems , Берлин, Гейдельберг: Springer Berlin Heidelberg, стр. 217–251, doi :10.1007/978-3-642-20441-8_9, ISBN 978-3-642-20440-1, получено 2023-04-02
7. Таллок, Гордон (1967). «Общая нерелевантность общей теоремы о невозможности». The Quarterly Journal of Economics . 81 (2): 256–270. doi :10.2307/1879585. JSTOR  1879585.
8. Жан-Франсуа Ласлье (2011). И проигравшим оказывается... Множественное голосование. ISBN 978-3-642-42955-2. ISSN  2267-828X. Wikidata  Q108664719. {{cite book}}: |journal=проигнорировано ( помощь )
9. Болл, Теренс и Антис Лоизидес, «Джеймс Милль», Стэнфордская энциклопедия философии (зимнее издание 2020 г.), Эдвард Н. Залта (ред.).
10. Нотация определена в статье Нормальное распределение§Нотация . Предположение о нормальности удобно и обеспечивает генеративную модель, пригодную для использования в симуляциях, но результаты Кондорсе и Янга не опираются на него, будучи выведенными из чистой теории вероятностей.
11. Янг, HP (1988). «Теория голосования Кондорсе». American Political Science Review . 82 (4): 1231–1244. doi :10.2307/1961757. ISSN  0003-0554. JSTOR  1961757. S2CID  14908863.
12. Бордли, Роберт Ф. (март 1983 г.). «Прагматический метод оценки избирательных схем посредством моделирования». American Political Science Review . 77 (1): 123–141. doi :10.2307/1956015. ISSN  0003-0554. JSTOR  1956015. S2CID  147689260.
13. Куинн, Джеймсон (2017-02-10). "Часто задаваемые вопросы об эффективности удовлетворенности избирателей". Страницы GitHub . Получено 24-07-2019 .
14. Грофман, Бернард; Фелд, Скотт Л. (декабрь 2004 г.). «Если вам нравится альтернативное голосование (также известное как мгновенный тур), то вам следует знать о правиле Кумбса». Electoral Studies . 23 (4): 641–659. doi :10.1016/j.electstud.2003.08.001.
15. Tideman, T. Nicolaus; Plassmann, Florenz (март 2014 г.). «Какое правило голосования с наибольшей вероятностью выберет «лучшего» кандидата?». Public Choice . 158 (3–4): 331–357. doi :10.1007/s11127-012-9935-y. ISSN  0048-5829. S2CID  189841413.
16. Дарлингтон, Ричард Б. (2018). «Являются ли системы голосования Кондорсе и минимакс лучшими?». arXiv : 1807.01366v8 [physics.soc-ph].
17. Дарлингтон, Ричард Б. (2016). «Минимакс — лучшая избирательная система в конце концов». arXiv : 1606.04371 [stat.ME].
18. Green-Armytage, James; Tideman, T. Nicolaus; Cosman, Rafael (январь 2016 г.). «Статистическая оценка правил голосования» (PDF) . Social Choice and Welfare . 46 (1): 183–212. doi :10.1007/s00355-015-0909-0. ISSN  0176-1714. S2CID  253842768.
19. Green-Armytage, Джеймс (январь 2014 г.). «Стратегическое голосование и номинация». Social Choice and Welfare . 42 (1): 111–138. doi :10.1007/s00355-013-0725-3. ISSN  0176-1714. S2CID  253847024.
20. Merrill, Samuel (февраль 1984 г.). «Сравнение эффективности многокандидатных избирательных систем». American Journal of Political Science . 28 (1): 23–48. doi :10.2307/2110786. JSTOR  2110786 – через JSTOR.
21. Лейпхарт, Аренд (март 1997 г.). «Неравное участие: неразрешенная дилемма демократии». American Political Science Review . 91 (1): 1–14. doi : 10.2307/2952255. JSTOR  2952255. S2CID  143172061.
22. Блэ, Андре (1990). «Способствует ли пропорциональное представительство явке избирателей?». Европейский журнал политических исследований . 18 (2): 167–181. doi :10.1111/j.1475-6765.1990.tb00227.x.
23. Таллок, Гордон (1965). «Входные барьеры в политику». The American Economic Review . 55 (1/2). Американская экономическая ассоциация: 458–466. ISSN  0002-8282. JSTOR  1816288. Получено 03.04.2024 .
24. Васильев, Сергей (1 апреля 2008 г.), Кардинальное голосование: способ избежать невозможности социального выбора , SSRN eLibrary, SSRN  1116545
25. Согласованность подразумевает участие, но не наоборот. Например, диапазонное голосование соответствует участию и согласованности, но срединные рейтинги удовлетворяют участию и не соответствуют согласованности.
26. Вудолл, Дуглас (декабрь 1994 г.), «Свойства правил преференциальных выборов», Voting Matters (3)
27. Смолл, Алекс (22 августа 2010 г.), «Геометрическое построение методов голосования, защищающих первый выбор избирателей», arXiv : 1008.4331 [cs.GT]
28. Таллок, Гордон (1965). «Входные барьеры в политику». The American Economic Review . 55 (1/2): 458–466. JSTOR  1816288.
29. МакГанн, Энтони Дж. и Майкл Латнер. «Исчисление консенсусной демократии: переосмысление моделей демократии без игроков с правом вето». Сравнительные политические исследования 46.7 (2013): 823-850.
30. Дисс, Мостафа; Догми, Ахмед (2016). «Методы подсчета результатов выборов с несколькими победителями: последовательность Кондорсе и парадоксы». Public Choice . 169 (1–2): 97–116. doi :10.1007/s11127-016-0376-x. ISSN  0048-5829. S2CID  73721191.
31. Эми, Дуглас Дж.; За избирательным урнами: руководство для граждан по системам голосования , стр. 120 ISBN 0275965864