Теорема Рамсея

Положение по математической комбинаторике

В комбинаторике теорема Рэмси в одной из своих теоретико-графовых форм утверждает, что монохроматические клики можно найти в любой маркировке ребер (цветами) достаточно большого полного графа . Чтобы продемонстрировать теорему для двух цветов (скажем, синего и красного), пусть r и s — любые два положительных целых числа . ^[1] Теорема Рэмси утверждает, что существует наименьшее положительное целое число R ( r , s ) , для которого каждая сине-красная раскраска ребер полного графа на R ( r , s ) вершинах содержит синюю клику на r вершинах или красную клику на s вершинах. (Здесь R ( r , s ) означает целое число, которое зависит как от r , так и от s .)

Теорема Рамсея — основополагающий результат комбинаторики. Первую версию этого результата доказал Фрэнк Рэмзи . Это положило начало комбинаторной теории, которая теперь называется теорией Рамсея , которая ищет регулярность среди беспорядка: общие условия существования подструктур с регулярными свойствами. В этом приложении речь идет о существовании одноцветных подмножеств , то есть подмножеств соединенных ребер только одного цвета.

Расширение этой теоремы применимо к любому конечному числу цветов, а не только к двум. Точнее, теорема утверждает, что для любого заданного числа цветов _{c и любых целых чисел n 1 , …, nc существует} число R ( _n 1 , … , nc ) _такое , что если ребра Полный граф порядка R ( n ₁ , …, nc ) раскрашен в c разных цветов, то для некоторого i от 1 до c он должен содержать полный подграф порядка n _{i ,} все ребра которого имеют цвет i . В приведенном выше частном случае c = 2 (и n ₁ = r и n ₂ = s ).

Примеры

р(3, 3) = 6

Двухцветное доказательство без слов. Из-за принципа «ячейки» из произвольной вершины v
есть как минимум 3 ребра одного цвета (пунктирный фиолетовый) . Назвав 3 вершины, завершающие эти ребра , r , s и t , если бы ребро rs , st или tr (сплошной черный) имело этот цвет, это завершило бы треугольник с помощью v . Но если нет, то каждый из них должен быть противоположного цвета, образуя треугольник этого цвета первым .

Разметка 2-х ребер K ₅ без монохроматического K ₃

Предположим, что ребра полного графа на 6 вершинах окрашены в красный и синий цвета. Выберите вершину, v . Есть 5 ребер, инцидентных v , поэтому (по принципу ячейки ) по крайней мере 3 из них должны быть одного цвета. Без ограничения общности мы можем предположить, что по крайней мере три из этих ребер, соединяющих вершину v с вершинами r , s и t , синие. (Если нет, поменяйте местами красный и синий в дальнейшем.) Если какие-либо из ребер ( rs ) , ( rt ) , ( st ) также синие, то у нас есть полностью синий треугольник. Если нет, то все эти три края красные, и мы имеем полностью красный треугольник. Поскольку этот аргумент работает для любой раскраски, любой K ₆ содержит одноцветный K ₃ , и, следовательно, R (3, 3) ⩽ 6 . Популярная версия этого утверждения называется теоремой о друзьях и незнакомцах .

Альтернативное доказательство работает путем двойного счета . Это происходит следующим образом: подсчитайте количество упорядоченных троек вершин x , y , z , таких, что ребро ( xy ) красное, а ребро ( yz ) синее. Во-первых, любая данная вершина будет серединой либо 0 × 5 = 0 (все ребра из вершины одного цвета), 1 × 4 = 4 (четыре — одного цвета, одно — другого цвета) или 2 × 3 = 6 (три одного цвета, две другого цвета) таких троек. Следовательно, таких троек не более 6 × 6 = 36 . Во-вторых, для любого неодноцветного треугольника ( xyz ) существует ровно две такие тройки. Следовательно, существует не более 18 неодноцветных треугольников. Следовательно, по крайней мере 2 из 20 треугольников в К ₆ одноцветные.

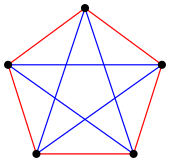
И наоборот, можно раскрасить K ₅ в два цвета, не создавая монохроматического K ₃ , показывая, что R (3, 3) > 5 . Уникальная расцветка ^[a] показана справа. Таким образом R (3, 3) = 6 .

Задача доказать, что R (3, 3) ≤ 6, была одной из задач математической олимпиады Уильяма Лоуэлла Патнэма в 1953 году, а также венгерской математической олимпиады в 1947 году.

Многоцветный пример:р(3, 3, 3) = 17

Единственные две 3-раскраски К ₁₆ без одноцветного К ₃ с точностью до изоморфизма и перестановки цветов: раскрученная (левая) и скрученная (правая) раскраски.

Многоцветное число Рамсея — это число Рамсея, состоящее из 3 или более цветов. Существует (с точностью до симметрии) только два нетривиальных многоцветных числа Рамсея, для которых известно точное значение, а именно R (3, 3, 3) = 17 и R (3, 3, 4) = 30 . ^[2]

Предположим, что у нас есть раскраска ребер полного графа в три цвета: красный, зеленый и синий. Предположим далее, что в раскраске ребер нет одноцветных треугольников. Выберите вершину v . Рассмотрим набор вершин, имеющих красное ребро к вершине v . Это называется красной окрестностью v . Красная окрестность v не может содержать красных ребер, так как в противном случае был бы красный треугольник, состоящий из двух концов этого красного ребра и вершины v . Таким образом, индуцированная раскраска ребер в красной окрестности точки v имеет ребра, окрашенные только в два цвета, а именно в зеленый и синий. Поскольку R (3, 3) = 6 , красная окрестность точки v может содержать не более 5 вершин. Аналогично, зеленая и синяя окрестности v могут содержать не более 5 вершин каждая. Поскольку каждая вершина, кроме самой v , находится в одной из красных, зеленых или синих окрестностей вершины v , весь полный граф может иметь не более 1 + 5 + 5 + 5 = 16 вершин. Таким образом, имеем R (3, 3, 3) ≤ 17 .

Чтобы увидеть, что R (3, 3, 3) = 17 , достаточно провести раскраску ребер на полном графе из 16 вершин тремя цветами, избегающую одноцветных треугольников. Оказывается, таких раскрасок на K ₁₆ ровно две , так называемые раскрученная и раскрученная раскраски. Обе раскраски показаны на рисунках справа: раскрученная раскраска слева, а скрученная раскраска справа.

Граф Клебша

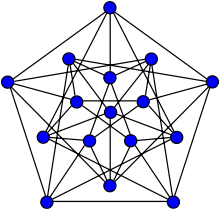
Если мы выберем любой цвет либо раскрученной, либо скрученной раскраски на K ₁₆ и рассмотрим граф, ребра которого являются именно теми ребрами, которые имеют указанный цвет, мы получим граф Клебша .

Известно, что существует ровно две рёберные раскраски в 3 цвета на K ₁₅ , избегающие одноцветных треугольников, которые можно построить удалением любой вершины из раскрученной и скрученной раскрасок на K ₁₆ соответственно.

Известно также, что существует ровно 115 раскрасок ребер в 3 цвета на К ₁₄ , избегающих одноцветных треугольников, при условии, что раскраски ребер, отличающиеся перестановкой цветов, мы считаем одинаковыми.

Доказательство

2-цветный корпус

Теорему для двухцветного случая можно доказать индукцией по r + s . ^[3] Из определения ясно, что для всех n R ( n , 2) = R (2, n ) = n . Это запускает индукцию. Мы докажем, что R ( r , s ) существует, найдя для него явную оценку. По индуктивному предположению R ( r − 1, s ) и R ( r , s − 1) существуют.

Лемма 1. ${\displaystyle R(r,s)\leq R(r-1,s)+R(r,s-1).}$

Доказательство. Рассмотрим полный граф на R ( r − 1, s ) + R ( r , s − 1) вершин, ребра которого раскрашены в два цвета. Выберите вершину v из графа и разделите оставшиеся вершины на два множества M и N так, чтобы для каждой вершины w w находился в M , если ребро ( vw ) синее, и w было в N , если ( vw ) красное. . Поскольку граф имеет вершины, отсюда следует, что либо или В первом случае, если M имеет красный K _s , то и исходный граф тоже имеет красные точки, и на этом мы закончили. В противном случае M имеет синий K _{r − 1} , а также синий K _r по определению M . Последний случай аналогичен. Таким образом, утверждение верно, и мы завершили доказательство для двух цветов. ${\displaystyle R(r-1,s)+R(r,s-1)=|M|+|N|+1}$ ${\displaystyle |M|\geq R(r-1,s)}$ ${\displaystyle |N|\geq R(r,s-1).}$ ${\displaystyle M\cup \{v\}}$

В этом двухцветном случае, если R ( r − 1, s ) и R ( r , s − 1) четные, неравенство индукции можно усилить до: ^[4]

${\displaystyle R(r,s)\leq R(r-1,s)+R(r,s-1)-1.}$

Доказательство . Предположим, что p = R ( r − 1, s ) и q = R ( r , s − 1) четные. Пусть t = p + q − 1 и рассмотрим двухцветный граф из t вершин. Если d _i — степень i -й вершины в синем подграфе, то по лемме о рукопожатии она четна. Учитывая, что t нечетное, должно быть четное d _i . Без ограничения общности предположим, что d ₁ четно и что M и N — вершины, инцидентные вершине 1 в синем и красном подграфах соответственно. Тогда оба и четны. По принципу Пидженхола либо или Поскольку четно, а p – 1 нечетно, первое неравенство можно усилить, поэтому либо или Предположим , что либо подграф M имеет красный K _s и доказательство завершено, либо он имеет синий K _{r – 1} , который вместе с вершиной 1 образует синий K _r . Случай рассматривается аналогично. ${\displaystyle \textstyle \sum _{i=1}^{t}d_{i}}$ ${\displaystyle |M|=d_{1}}$ ${\displaystyle |N|=t-1-d_{1}}$ ${\displaystyle |M|\geq p-1,}$ ${\displaystyle |N|\geq q.}$ ${\displaystyle |M|}$ ${\displaystyle |M|\geq p}$ ${\displaystyle |N|\geq q.}$ ${\displaystyle |M|\geq p=R(r-1,s).}$ ${\displaystyle |N|\geq q=R(r,s-1)}$

Случай большего количества цветов

Лемма 2. Если c > 2 , то ${\displaystyle R(n_{1},\dots ,n_{c})\leq R(n_{1},\dots ,n_{c-2},R(n_{c-1},n_{c})).}$

Доказательство. Рассмотрим полный граф вершин и раскрасим его ребра в c цветов. Теперь «станьте дальтоником» и представьте, что c − 1 и c — один и тот же цвет. Таким образом, граф теперь ( c − 1) -цветный. В силу определения такой граф содержит либо K _{n i,} одноцветно окрашенный в цвет i для некоторого 1 ≤ i ≤ c − 2 , либо K _{R ( n c − 1 , nc )} - раскрашенный в «размытый цвет _» '. В первом случае мы закончили. В последнем случае мы снова обретаем зрение и видим, что из определения R ( n _{c − 1} , n _c ) мы должны иметь либо a ( c − 1) -монохром K _{n c - 1} , либо c -монохром K _{n в} . В любом случае доказательство завершено. ${\displaystyle R(n_{1},\dots ,n_{c-2},R(n_{c-1},n_{c}))}$ ${\displaystyle R(n_{1},\dots ,n_{c-2},R(n_{c-1},n_{c})),}$

Из леммы 1 следует, что любой R ( r , s ) конечен. Правая часть неравенства в лемме 2 выражает число Рамсея для c цветов через числа Рамсея для меньшего числа цветов. Следовательно, любой R ( n 1 _, …, nc ₎ конечен для любого числа цветов. Это доказывает теорему.

Числа Рэмзи

Числа R ( r , s ) в теореме Рамсея (и их расширения до более чем двух цветов) известны как числа Рамсея. Число Рэмси R ( m , n ) дает решение задачи о вечеринке, которая требует минимального количества гостей R ( m , n ) , которые должны быть приглашены, чтобы хотя бы m знали друг друга или хотя бы n были не знать друг друга. На языке теории графов число Рамсея — это минимальное количество вершин v = R ( m , n ) , такое, что все неориентированные простые графы порядка v содержат клику порядка m или независимое множество порядка n. . Теорема Рамсея утверждает, что такое число существует для всех m и n .

По симметрии верно, что R ( m , n ) = R ( n , m ) . Верхняя оценка для R ( r , s ) может быть получена из доказательства теоремы, а другие аргументы дают нижние оценки. (Первая экспоненциальная нижняя граница была получена Полом Эрдешем с использованием вероятностного метода .) Однако существует огромный разрыв между самыми точными нижними и самыми точными верхними границами. Существует также очень мало чисел r и s , для которых мы знаем точное значение R ( r , s ) .

Вычисление нижней границы L для R ( r , s ) обычно требует демонстрации синей/красной раскраски графа K _{L −1} без синего подграфа K _r и красного подграфа K _s . Такой контрпример называется графом Рамсея . Брендан Маккей ведет список известных графов Рэмси. ^[5] Верхние оценки зачастую установить значительно сложнее: нужно либо проверить все возможные раскраски, чтобы подтвердить отсутствие контрпримера, либо представить математическое обоснование его отсутствия.

Вычислительная сложность

Эрдеш просит нас представить инопланетную силу, намного более мощную, чем мы, приземлившуюся на Землю и требующую значение R (5, 5) , иначе они уничтожат нашу планету. В этом случае, утверждает он, нам следует собрать все наши компьютеры и всех наших математиков и попытаться найти значение. Но предположим, что вместо этого они просят R (6, 6) . В таком случае, считает он, нам следует попытаться уничтожить инопланетян. ^[6]

—  Джоэл Спенсер

Сложная компьютерная программа не требует рассматривать все раскраски по отдельности, чтобы исключить их все; тем не менее, это очень сложная вычислительная задача, с которой существующее программное обеспечение может справиться только при небольших размерах. Каждый полный граф K _n имеет ⁠1/2⁠ n ( n - 1) ребер, так что всего будет c ^{n ( n -1)/2} графов для поиска (для c цветов), если используется грубая сила. ^[7] Таким образом, сложность поиска всех возможных графов (с помощью грубой силы ) равна O ( c ^{n 2} ) для c раскрасок и не более n узлов.

Ситуация вряд ли улучшится с появлением квантовых компьютеров . Один из самых известных алгоритмов поиска неструктурированных наборов данных демонстрирует только квадратичное ускорение (см. алгоритм Гровера ) по сравнению с классическими компьютерами, так что время вычислений по-прежнему экспоненциально зависит от количества узлов. ^{[8] [9]}

Известные значения

Как описано выше, R (3, 3) = 6 . Легко доказать, что R (4, 2) = 4 и, в более общем смысле, что R ( s , 2) = s для всех s : граф на s − 1 узлах со всеми ребрами, окрашенными в красный цвет, служит контрпримером и доказывает, что R ( s , 2) ≥ s ; Среди раскрасок графа на s узлах раскраска, в которой все ребра окрашены в красный цвет, содержит красный подграф s -узла, а все остальные раскраски содержат 2-узловой синий подграф (т. е. пару узлов, соединенных синим ребром).

Используя неравенства индукции и лемму о согласовании , можно заключить, что R (4, 3) ⩽ R (4, 2) + R (3, 3) − 1 = 9 , и, следовательно, R (4, 4) ⩽ R (4 , 3) + Р (3, 4) ≤ 18 . Среди 6,4 × 10 ²² различных 2-раскрасок 16-узловых графов существует только два (4, 4, 16) графа (т. е. 2-раскраски полного графа на 16 узлах без 4-узловых красных или синих полных подграфов). , и только один (4, 4, 17) граф ( граф Пэли порядка 17) среди 2,46 × 10 ²⁶ раскрасок. ^[5] (Это было доказано Эвансом, Пулемом и Шиханом в 1979 году.) Отсюда следует, что R (4, 4) = 18 .

Тот факт, что R (4, 5) = 25, был впервые установлен Бренданом Маккеем и Станиславом Радзишовским в 1995 году. ^[10]

Точное значение R (5, 5) неизвестно, хотя известно, что оно лежит между 43 (Джеффри Экзоо (1989) ^[11] ) и 48 (Ангельтвейт и Маккей (2017) ^[12] ) включительно.

В 1997 году Маккей, Радзишовский и Эксоо с помощью компьютерных методов создания графов предположили, что R (5, 5) = 43 . Им удалось построить ровно 656 (5, 5, 42) графов, придя к одному и тому же набору графов разными путями. Ни один из 656 графов не может быть расширен до графа (5, 5, 43) . ^[13]

Для R ( r , s ) с r , s > 5 доступны только слабые оценки. Нижние границы для R (6, 6) и R (8, 8) не улучшались с 1965 и 1972 годов соответственно. ^[2]

R ( r , s ) с r , s ≤ 10 показаны в таблице ниже. Если точное значение неизвестно, в таблице перечислены наиболее известные границы. R ( r , s ) с r < 3 задаются формулами R (1, s ) = 1 и R (2, s ) = s для всех значений s .

Стандартным обзором развития исследований чисел Рамсея является Динамический обзор 1 Электронного журнала комбинаторики Станислава Радзишовского , который периодически обновляется. ^{[2] [14]} Если не указано иное, записи в таблице ниже взяты из издания за январь 2021 года. (Обратите внимание, что существует тривиальная симметрия по диагонали, поскольку R ( r , s ) = R ( s , r ) .)

Асимптотика

Неравенство R ( r , s ) ≤ R ( r − 1, s ) + R ( r , s − 1) можно применить индуктивно, чтобы доказать, что

${\displaystyle R(r,s)\leq {\binom {r+s-2}{r-1}}.}$

В частности, из этого результата Эрдеша и Секереша следует, что когда r = s ,

${\displaystyle R(s,s)\leq (1+o(1)){\frac {4^{s-1}}{\sqrt {\pi s}}}.}$

Экспоненциальная нижняя граница,

${\displaystyle R(s,s)\geq (1+o(1)){\frac {s}{{\sqrt {2}}e}}2^{s/2},}$

была дана Эрдёшем в 1947 году и сыграла важную роль во внедрении вероятностного метода. Между этими двумя границами существует огромный разрыв: например, для s = 10 это дает 101 ≤ R (10, 10) ≤ 48,620 . Тем не менее, коэффициенты экспоненциального роста для обеих оценок не улучшались в течение длительного времени, а для нижней границы они все еще составляют √ 2 . Не существует известной явной конструкции, дающей экспоненциальную нижнюю оценку. Наиболее известные нижняя и верхняя границы диагональных чисел Рамсея:

${\displaystyle [1+o(1)]{\frac {{\sqrt {2}}s}{e}}2^{\frac {s}{2}}\leq R(s,s)\leq s^{-(c\log s)/(\log \log s)}4^{s},}$

благодаря Спенсеру и Конлону соответственно; Препринт Кампоса, Гриффитса, Морриса и Сахасрабуде 2023 года утверждает, что добился экспоненциального прогресса, используя алгоритмическую конструкцию, основанную на графовой структуре, называемой « книгой », ^{[18] [19]} улучшая верхнюю границу до

${\displaystyle R(s,s)\leq (4-\varepsilon )^{s}{\text{ and }}R(s,t)\leq e^{-\delta t+o(s)}{\binom {s+t}{t}}.}$

с и где предполагается, что эти параметры могут быть оптимизированы, в частности . ${\displaystyle \varepsilon =2^{-7}}$ ${\displaystyle \delta =50^{-1}}$ ${\displaystyle \varepsilon }$

Для недиагональных чисел Рамсея R (3, t ) известно, что они имеют порядок ⁠т ²/журнал т⁠ ; это можно сформулировать эквивалентно тому, что наименьшее возможное число независимости в графе без треугольников с n вершинамиравно

${\displaystyle \Theta \left({\sqrt {n\log n}}\right).}$

Верхняя оценка для R (3, t ) дана Айтаи , Комлосом и Семереди , ^[20] нижняя оценка была первоначально получена Кимом , ^[21] , а неявная константа была улучшена независимо Фисом Понтиверосом, Гриффитсом и Моррисом , ^[22] и Бохман и Киваш ^[23] путем анализа процесса без треугольников . Более того, изучение более общего « H -свободного процесса» установило наиболее известные асимптотические нижние оценки для общих недиагональных чисел Рамсея: ^[24] R ( s , t )

${\displaystyle c'_{s}{\frac {t^{\frac {s+1}{2}}}{(\log t)^{{\frac {s+1}{2}}-{\frac {1}{s-2}}}}}\leq R(s,t)\leq c_{s}{\frac {t^{s-1}}{(\log t)^{s-2}}}.}$

Границы становятся , но в препринте 2023 года ^{[25] [26]} была улучшена нижняя граница, что решает вопрос об Эрдеше, который предложил 250 долларов за доказательство того, что нижний предел имеет форму . ^{[27] [28]} ${\displaystyle s=4}$ ${\displaystyle c'_{s}t^{\frac {5}{2}}(\log t)^{-2}\leq R(4,t)\leq c_{s}t^{3}(\log t)^{-2}}$ ${\displaystyle c'_{s}t^{3}(\log t)^{-4}}$ ${\displaystyle c'_{s}t^{3}(\log t)^{-d}}$

Индуцированный Рэмси

Существует менее известный, но интересный аналог теоремы Рамсея для индуцированных подграфов . Грубо говоря, теперь вместо поиска монохроматического подграфа нам необходимо найти монохроматический индуцированный подграф. В этом варианте уже недостаточно ограничивать наше внимание полными графами , поскольку существование полного подграфа не подразумевает существование индуцированного подграфа. Качественная формулировка теоремы в следующем разделе была впервые независимо доказана Эрдёшем , Хайналом и Посой , Дойбером и Рёдлем в 1970-х годах. ^{[29] [30] [31]} С тех пор было проведено много исследований по получению хороших оценок для индуцированных чисел Рамсея.

Заявление

Пусть H — граф на n вершинах. Тогда существует граф G такой, что любая раскраска ребер G в два цвета содержит монохроматическую индуцированную копию H ( т.е. индуцированный подграф G такой , что он изоморфен H и его ребра одноцветны). Наименьшее возможное число вершин графа G — это индуцированное число Рамсея r _ind ( H ) .

Иногда мы рассматриваем и асимметричный вариант проблемы. Мы определяем r _ind ( X , Y ) как наименьшее возможное количество вершин графа G такое, что каждая раскраска ребер G с использованием только красного или синего цвета содержит красный индуцированный подграф X или синий индуцированный подграф Y .

История и границы

Как и в случае с теоремой Рамсея, априори неясно, существуют ли индуцированные числа Рамсея для каждого графа H . В начале 1970-х годов Эрдеш , Хайнал и Поса , Дойбер и Рёдль независимо друг от друга доказали, что это так. ^{[29] [30] [31]} Однако первоначальные доказательства давали ужасные ограничения (например, башни из двоек ) на индуцированные числа Рамсея. Интересно задаться вопросом, можно ли достичь лучших границ. В 1974 году Пол Эрдеш предположил, что существует константа c такая, что каждый граф H на k вершинах удовлетворяет условию r _ind ( H ) ≤ 2 ^ck . ^[32] Если эта гипотеза верна, она будет оптимальной до константы c, поскольку полный граф достигает нижней границы этого вида (фактически это то же самое, что и числа Рамсея). Однако на данный момент эта гипотеза все еще остается открытой.

В 1984 году Эрдеш и Хайнал заявили, что доказали связь ^[33]

${\displaystyle r_{\text{ind}}(H)\leq 2^{2^{k^{1+o(1)}}}.}$

Однако это все еще было далеко от экспоненциальной границы, предполагаемой Эрдёшем. Лишь в 1998 году крупный прорыв был достигнут Кохаякавой , Премелем и Рёдлем, которые доказали первую почти экспоненциальную оценку r _ind ( H ) ≤ 2 ^{ck (log k ) 2} для некоторой постоянной c . Их подход заключался в том, чтобы рассмотреть подходящий случайный граф, построенный на проективных плоскостях , и показать, что он обладает желаемыми свойствами с ненулевой вероятностью. Идея использования случайных графов на проективных плоскостях ранее также использовалась при изучении свойств Рамсея относительно раскрасок вершин и индуцированной проблемы Рамсея на графах ограниченной степени H . ^[34]

Граница Кохаякавы, Премеля и Рёдля оставалась лучшей общей оценкой за десятилетие. В 2008 году Фокс и Судаков предоставили явную конструкцию индуцированных чисел Рамсея с той же оценкой. ^[35] Фактически они показали, что каждый ( n , d ,λ) -граф G с малым λ и подходящим d содержит индуцированную монохроматическую копию любого графа на k вершинах в любой раскраске ребер G в два цвета. В частности, для некоторой константы c граф Пэли на n ≥ 2 ^{ck log 2 k} вершин таков, что все его раскраски ребер в два цвета содержат индуцированную монохроматическую копию каждого k -графа вершин.

В 2010 году Конлон , Фокс и Судаков смогли улучшить оценку до r _ind ( H ) ≤ 2 ^{ck log k} , которая остается на данный момент лучшей верхней границей для общих индуцированных чисел Рамсея. ^[36] Как и в предыдущей работе 2008 года, они показали, что каждый ( n , d ,λ) -граф G с малым λ и плотностью ребер 1 ⁄ 2 содержит индуцированную монохроматическую копию каждого графа на k вершинах в любой раскраске ребер в два цвета. В настоящее время гипотеза Эрдёша о том, что r _ind ( H ) ≤ 2 ^ck, остаётся открытой и является одной из важных проблем экстремальной теории графов .

Что касается нижних оценок, в целом известно немногое, за исключением того факта, что индуцированные числа Рамсея должны быть по крайней мере соответствующими числами Рамсея. Для некоторых частных случаев получены некоторые нижние оценки (см. «Особые случаи»).

Особые случаи

Хотя общие оценки индуцированных чисел Рамсея экспоненциальны по размеру графа, их поведение сильно отличается на специальных классах графов (в частности, на разреженных). Многие из этих классов индуцировали числа Рамсея, полиномиальные по числу вершин.

Если H — цикл , путь или звезда на k вершинах, известно, что r _ind ( H ) линеен по k . ^[35]

Если H — дерево с k вершинами, известно, что r _ind ( H ) = O ( k ² log ² k ) . ^[37] Также известно, что r _ind ( H ) является суперлинейным (т.е. r _ind ( H ) = ω( k ) ). Обратите внимание, что это контрастирует с обычными числами Рамсея, где гипотеза Берра–Эрдёша (теперь доказанная) говорит нам, что r ( H ) линейно (поскольку деревья 1- вырождены ).

Для графов H с числом вершин k и ограниченной степенью Δ была выдвинута гипотеза, что r _ind ( H ) ⩽ cn ^{d (Δ)} для некоторой константы d , зависящей только от Δ . Этот результат был впервые доказан Лучаком и Рёдлем в 1996 году, когда d (Δ) росла как башня из двоек высотой O (Δ ² ) . ^[38] С тех пор были получены более разумные оценки для d (∆) . В 2013 году Конлон, Фокс и Чжао показали, используя лемму о подсчете для разреженных псевдослучайных графов , что r _ind ( H ) ≤ cn ^2Δ+8 , где показатель степени является максимально возможным с точностью до постоянных множителей. ^[39]

Обобщения

Подобно числам Рамсея, мы можем обобщить понятие индуцированных чисел Рамсея на гиперграфы и многоцветные настройки.

Больше цветов

Мы также можем обобщить индуцированную теорему Рамсея на многоцветный случай. Для графов H ₁ , H ₂ , …, H _r определите r _ind ( H ₁ , H ₂ , …, H _r ) как минимальное число вершин в графе G такое, что любая раскраска ребер G в r цвета содержат индуцированный подграф, изоморфный H _i, где все ребра окрашены в i -й цвет для некоторого 1 ≤ i ≤ r . Пусть r _ind ( H ; q ) := r _ind ( H , H , …, H ) ( q копий H ).

Можно получить оценку для r _ind ( H ; q ) , которая примерно представляет собой башню из двух высотой ~ log q , итеративно применяя оценку к двухцветному случаю. Самая известная на данный момент оценка принадлежит Фоксу и Судакову, которые достигают r _ind ( H ; q ) ≤ 2 ^{ck 3} , где k — количество вершин H , а c — константа, зависящая только от q . ^[40]

Гиперграфики

Мы можем расширить определение индуцированных чисел Рамсея на d -однородные гиперграфы, просто заменив слово « граф» в утверждении на «гиперграф» . Более того, мы можем определить многоцветную версию индуцированных чисел Рамсея так же, как и в предыдущем подразделе.

Пусть H — d -однородный гиперграф с k вершинами. Определите функцию башни t _r ( x ) , полагая t ₁ ( x ) = x и для i ≥ 1 , t _{i +1} ( x ) = 2 ^{t _i ( x )} . Используя метод контейнера гиперграфа, Конлон, Делламоника, Ла Флер, Рёдль и Шахт смогли показать, что для d ≥ 3, q ​​≥ 2 , r _ind ( H ; q ) ≤ t _d ( ck ) для некоторой константы c, зависящей только от д и q . В частности, этот результат отражает наиболее известную оценку обычного числа Рамсея при d = 3 . ^[41]

Расширения теоремы

Бесконечные графы

Следующий результат, также известный как теорема Рамсея , применим к бесконечным графам. В контексте, где также обсуждаются конечные графы, ее часто называют «бесконечной теоремой Рамсея». Поскольку интуиция, обеспечиваемая графическим представлением графа, уменьшается при переходе от конечных графов к бесконечным, теоремы в этой области обычно формулируются в теоретико-множественной терминологии. ^[42]

Теорема. Пусть некоторое бесконечное множество и раскрасьте элементы (подмножества размера ) в разные цвета. Тогда существует такое бесконечное подмножество , что все подмножества размеров имеют один и тот же цвет. ${\displaystyle X}$ ${\displaystyle [X]^{n}}$ ${\displaystyle X}$ ${\displaystyle n}$ ${\displaystyle c}$ ${\displaystyle M}$ ${\displaystyle X}$ ${\displaystyle n}$ ${\displaystyle M}$

Доказательство : Доказательство проводится индукцией по n , размеру подмножеств. Для n = 1 это утверждение эквивалентно утверждению, что если вы разделите бесконечное множество на конечное число множеств, то одно из них будет бесконечным. Это очевидно. Предполагая, что теорема верна для n ⩽ r , докажем ее для n = r + 1 . Учитывая c -раскраску подмножеств ( r + 1) -элементов X , пусть a ₀ будет элементом X и пусть Y = X \ { a ₀ }. Затем мы вызываем c -раскраску подмножеств r -элементов Y , просто добавляя 0 к каждому подмножеству r -элемента (чтобы получить ( r ₊ 1) -элементное подмножество X ). По предположению индукции существует бесконечное подмножество Y ₁ из Y такое, что каждое подмножество из r -элементов Y ₁ окрашено в один и тот же цвет при индуцированной раскраске. Таким образом, существуют элемент a ₀ и бесконечное подмножество Y ₁ такие, что все ( r + 1) -элементные подмножества X , состоящие из a ₀ и r элементов Y _1, имеют одинаковый цвет. По тому же рассуждению существует элемент a ₁ в Y ₁ и бесконечное подмножество Y ₂ из Y ₁ с теми же свойствами. Индуктивно мы получаем последовательность { a ₀ , a ₁ , a ₂ , …} такую, что цвет каждого ( r + 1) -элементного подмножества ( a _{i (1)} , a _{i (2)} , …, a _{i ( r + 1)} ) при i (1) < i (2) < … < i ( r + 1) зависит только от значения i (1). Далее, существует бесконечно много значений i ( n ) таких, что этот цвет будет одинаковым. Возьмите эти a _{i ( n )} , чтобы получить желаемый одноцветный набор.

Более сильная, но несбалансированная бесконечная форма теоремы Рэмси для графов, теорема Эрдеша-Душника-Миллера , утверждает, что каждый бесконечный граф содержит либо счетное бесконечное независимое множество, либо бесконечную клику той же мощности , что и исходный граф. ^[43]

Бесконечная версия подразумевает конечную

Конечную теорему Рамсея можно вывести из бесконечной версии путем доказательства от противного . Предположим, что конечная теорема Рамсея неверна. Тогда существуют целые числа c , n , T такие , что для каждого целого числа k существует c -раскраска [ k ] ^{( n )} без монохроматического множества размера T. Обозначим _через Ck c - раскраски [ k ] ^{( n )} без монохроматического множества размера T.

Для любого k ограничение раскраски в Ck _{+ 1} на [ k ] ^{( n )} (путем игнорирования цвета всех множеств, содержащих _k + 1 ) является раскраской в ​​Ck . Определим ⁠ ⁠ ${\displaystyle C_{k}^{1}}$ как раскраски в C _k , которые являются ограничениями раскрасок в C _{k +1} . Поскольку C _{k +1} не пуст, то и ⁠ ⁠ ${\displaystyle C_{k}^{1}}$ не пуст .

Точно так же ограничение любой раскраски в ⁠ ⁠ ${\displaystyle C_{k+1}^{1}}$ находится в ⁠ ⁠ ${\displaystyle C_{k}^{1}}$ , что позволяет определить ⁠ ⁠ ${\displaystyle C_{k}^{2}}$ как множество всех таких ограничений, непустое множество. Продолжая так, определим ⁠ ⁠ ${\displaystyle C_{k}^{m}}$ для всех целых чисел m , k .

Теперь для любого целого числа k

${\displaystyle C_{k}\supseteq C_{k}^{1}\supseteq C_{k}^{2}\supseteq \cdots }$

и каждое множество непусто. Более того, C _k конечен, поскольку

${\displaystyle |C_{k}|\leq c^{\frac {k!}{n!(k-n)!}}}$

Отсюда следует, что пересечение всех этих множеств непусто и пусть

${\displaystyle D_{k}=C_{k}\cap C_{k}^{1}\cap C_{k}^{2}\cap \cdots }$

Тогда каждая раскраска в _Dk является ограничением раскраски в Dk _{+ 1} . Следовательно, ограничивая раскраску в D _k раскраской в ​​D _{k +1} и продолжая делать это, можно построить раскраску без какого-либо монохроматического множества размера T . Это противоречит бесконечной теореме Рамсея. ${\displaystyle \mathbb {N} ^{(n)}}$

Если принять подходящую топологическую точку зрения, этот аргумент становится стандартным аргументом компактности, показывающим, что из бесконечной версии теоремы следует конечная версия. ^[44]

Гиперграфики

Теорему можно распространить и на гиперграфы . m -гиперграф — это граф, «ребра» которого представляют собой наборы из m вершин ; в обычном графе ребро представляет собой набор из двух вершин. Полное утверждение теоремы Рэмси для гиперграфов заключается в том, что для любых целых чисел m и c и любых целых чисел n ₁ , …, _nc существует целое число R ( n ₁ , …, nc ; _m ) такое, что если гиперребра полный m -гиперграф порядка R ( n ₁ , …, nc ; m ) раскрашен в c разных цветов, то для некоторого _i от 1 до c гиперграф должен содержать полный под- m -гиперграф порядка n _i все гиперребра которого имеют цвет i . Эту теорему обычно доказывают индукцией по m — «сверхточности» графа. Базовым случаем доказательства является m = 2 , что в точности соответствует приведенной выше теореме.

Для m = 3 мы знаем точное значение одного нетривиального числа Рамсея, а именно R (4, 4; 3) = 13 . Этот факт был установлен Бренданом Маккеем и Станиславом Радзишовским в 1991 году. ^[45] Кроме того, имеем: R (4, 5; 3) ≥ 35 , ^[46] R (4, 6; 3) ≥ 63 и R (5, 5 3) ≥ 88 ; ^[46]

Ориентированные графы

Также возможно определить числа Рамсея для ориентированных графов; они были введены П. Эрдешем и Л. Мозером (1964). Пусть R ( n ) — наименьшее число Q такое, что любой полный граф с однонаправленными дугами (также называемый «турниром») и с ≥ Q узлами содержит ациклический (также называемый «транзитивным») n -узловой подтурнир.

Это аналог ориентированного графа того, что (выше) было названо R ( n , n ; 2) , наименьшее число Z такое, что любая 2-раскраска ребер полного неориентированного графа с ≥ Z узлами содержит монохроматический полный граф на n узлах. (Направленный аналог двух возможных цветов дуг — это два направления дуг, аналог «монохроматического» — «все стрелки дуг направлены одинаково»; т. е. «ациклично».)

Имеем R (0) = 0 , R (1) = 1 , R (2) = 2 , R (3) = 4 , R (4) = 8 , R (5) = 14 , R (6) = 28. , и 34 ≤ R (7) ≤ 47 . ^{[47] [48]}

Несчетные кардиналы

В терминах исчисления разделов теорему Рэмси можно сформулировать как для всех конечных n и k . Вацлав Серпинский показал, что теорема Рамсея не распространяется на графы размера, показав, что . В частности, гипотеза континуума предполагает, что . Стево Тодорчевич показал, что на самом деле в ZFC гораздо более сильное утверждение, чем в . Джастин Т. Мур еще больше укрепил этот результат. С положительной стороны, кардинал Рамсея , , является большим кардиналом, аксиоматически определенным так, чтобы удовлетворять соответствующей формуле: . Существование кардиналов Рэмси не может быть доказано в ZFC. ${\displaystyle \aleph _{0}\rightarrow (\aleph _{0})_{k}^{n}}$ ${\displaystyle \aleph _{1}}$ ${\displaystyle 2^{\aleph _{0}}\nrightarrow (\aleph _{1})_{2}^{2}}$ ${\displaystyle \aleph _{1}\nrightarrow (\aleph _{1})_{2}^{2}}$ ${\displaystyle \aleph _{1}\nrightarrow [\aleph _{1}]_{\aleph _{1}}^{2}}$ ${\displaystyle \aleph _{1}\nrightarrow (\aleph _{1})_{2}^{2}}$ ${\displaystyle \kappa }$ ${\displaystyle \kappa \rightarrow (\kappa )_{2}^{<\omega }}$

Связь с аксиомой выбора

В обратной математике существует значительная разница в силе доказательства между версией теоремы Рэмси для бесконечных графов (случай n = 2) и для бесконечных мультиграфов (случай n ≥ 3). Версия теоремы с мультиграфом эквивалентна по силе аксиоме арифметического понимания , что делает ее частью подсистемы ACA ₀ арифметики второго порядка , одной из пяти больших подсистем обратной математики. Напротив, по теореме Дэвида Ситапуна графическая версия теоремы слабее, чем ACA ₀ , и (объединяя результат Ситапуна с другими) она не попадает ни в одну из больших пяти подсистем. ^[49] Однако над ZF из графовой версии следует классическая лемма Кенига , тогда как обратная импликация не выполняется, ^[50] поскольку лемма Кенига эквивалентна счетному выбору из конечных множеств в этой ситуации. ^[51]

Смотрите также

• Кардинал Рэмси
• Теорема Пэрис – Харрингтона
• Сим (игра с карандашами)
• Бесконечная теория Рамсея
• Число Ван дер Вардена
• Игра Рэмси
• Теорема Эрдеша – Радо

Примечания

1. с точностью до автоморфизмов графа

1. Некоторые авторы ограничивают значения величиной больше единицы, например (Brualdi 2010) и (Harary 1972), избегая тем самым обсуждения раскраски ребер графа без ребер, в то время как другие перефразируют формулировку теоремы, чтобы потребовать, в простой граф , либо r -клика, либо s - независимое множество , см. (Gross 2008) или (Erdős & Szekeres 1935). В таком виде рассмотрение графов с одной вершиной более естественно.
2. Радзишовский, Станислав (2011). «Малые числа Рамсея». Динамические опросы. Электронный журнал комбинаторики . 1000 . дои : 10.37236/21 .
3. До, Норман (2006). «Партийные проблемы и теория Рэмси» (PDF) . австр. Математика. Соц. Газета . 33 (5): 306–312.
4. «Партийные знакомые».
5. "Графики Рэмси".
6. Джоэл Х. Спенсер (1994), Десять лекций по вероятностному методу, SIAM , стр. 4, ISBN 978-0-89871-325-1
7. 2.6 Теория Рэмси из журнала Mathematics Illumination
8. Монтанаро, Эшли (2016). «Квантовые алгоритмы: обзор». npj Квантовая информация . 2 : 15023. arXiv : 1511.04206 . Бибкод : 2016npjQI...215023M. дои : 10.1038/npjqi.2015.23. S2CID  2992738 – через Nature.
9. Ван, Хэфэн (2016). «Определение чисел Рамсея на квантовом компьютере». Физический обзор А. 93 (3): 032301. arXiv : 1510.01884 . Бибкод : 2016PhRvA..93c2301W. doi : 10.1103/PhysRevA.93.032301. S2CID  118724989.
10. Маккей, Брендан Д.; Радзишовский, Станислав П. (май 1995 г.). «R(4,5) = 25» (PDF) . Журнал теории графов . 19 (3): 309–322. дои : 10.1002/jgt.3190190304.
11. Эксу, Джеффри (март 1989 г.). «Нижняя оценка для R (5, 5) ». Журнал теории графов . 13 (1): 97–98. дои : 10.1002/jgt.3190130113.
12. Виглейк Ангельтвейт; Брендан Маккей (сентябрь 2018 г.). " ". Журнал теории графов . 89 (1): 5–13. arXiv : 1703.08768v2 . дои : 10.1002/jgt.22235. ${\displaystyle R(5,5)\leq 48}$
13. Брендан Д. Маккей, Станислав П. Радзишовский (1997). «Идентификаторы подсчета подграфов и числа Рамсея» (PDF) . Журнал комбинаторной теории . Серия Б. 69 (2): 193–209. дои : 10.1006/jctb.1996.1741 .
14. Станислав Радзишовский. «ДС1» . Проверено 17 августа 2023 г.
15. Ангельтвейт, Виглейк (31 декабря 2023 г.). «R(3,10) <= 41». arXiv : 2401.00392 [math.CO].
16. Exoo, Джеффри; Татаревич, Милош (2015). «Новые нижние границы для 28 классических чисел Рамсея». Электронный журнал комбинаторики . 22 (3): 3. arXiv : 1504.02403 . Бибкод : 2015arXiv150402403E. дои : 10.37236/5254 .
17. Exoo, Джеффри (26 октября 2023 г.). «Нижняя граница для R (5,6)». arXiv : 2310.17099 [math.CO].
18. Кампос, Марсело; Гриффитс, Саймон; Моррис, Роберт; Сахасрабуде, Джулиан (2023). «Экспоненциальное улучшение диагонального Рэмси». arXiv : 2303.09521 [math.CO].
19. Сломан, Лейла (2 мая 2023 г.). «Очень большой маленький скачок вперед в теории графов». Журнал Кванта .
20. Айтай, Миклош; Комлос, Янош; Семереди, Эндре (1 ноября 1980 г.). «Заметка о числах Рамсея». Журнал комбинаторной теории, серия А. 29 (3): 354–360. дои : 10.1016/0097-3165(80)90030-8 . ISSN  0097-3165.
21. Ким, Чон Хан (1995), «Число Рэмси R (3, t ) имеет порядок величины t ² /log t », Случайные структуры и алгоритмы , 7 (3): 173–207, CiteSeerX 10.1.1.46.5058 , дои : 10.1002/rsa.3240070302 
22. «Процесс без треугольников и число Рэмси $R(3,k)$» . bookstore.ams.org . Проверено 27 июня 2023 г.
23. Бохман, Том; Киваш, Питер (17 ноября 2020 г.). «Динамическая концентрация процесса без треугольников». Случайные структуры и алгоритмы . 58 (2): 221–293. arXiv : 1302.5963 . дои : 10.1002/rsa.20973.
24. Бохман, Том; Киваш, Питер (01 августа 2010 г.). «Ранняя эволюция процесса без H». Математические изобретения . 181 (2): 291–336. arXiv : 0908.0429 . дои : 10.1007/s00222-010-0247-x. ISSN  1432-1297.
25. Маттеус, Сэм; Верстраете, Жак (5 марта 2024 г.). «Асимптотика r(4,t)». Анналы математики . arXiv : 2306.04007 . дои : 10.4007/анналы.2024.199.2.8.
26. Цепелевич, Джордана (22 июня 2023 г.). «Математики открывают новый способ прогнозирования структуры в графах». Журнал Кванта .
27. Эрдеш, Пол (1990), Нешетржил, Ярослав; Рёдль, Войтех (ред.), «Проблемы и результаты для графов и гиперграфов: сходства и различия», Математика теории Рамсея , алгоритмы и комбинаторика, Берлин, Гейдельберг: Springer, стр. 12–28, doi : 10.1007/978-3 -642-72905-8_2, ISBN 978-3-642-72905-8, получено 27 июня 2023 г.
28. "Проблемы Эрдёша" . www.erdosproblems.com . Проверено 12 июля 2023 г.
29. Эрдеш, П .; Хайнал, А.; Поса, Л. (1975). «Сильное вложение графов в цветные графы». Бесконечные и конечные множества, Vol. 1 . Коллоквиум Mathematica Societatis Яноса Бойяи. Том. 10. Северная Голландия, Амстердам/Лондон. стр. 585–595.
30. Дойбер, В. (1975). «Обобщение теоремы Рамсея». Бесконечные и конечные множества, Vol. 1 . Colloquia Mathematica Societatis Янош Бойай. Том. 10. Северная Голландия, Амстердам/Лондон. стр. 323–332.
31. Рёдль, В. (1973). Размерность графа и обобщенные теоремы Рамсея (магистерская диссертация). Карлов университет.
32. Эрдеш, П. (1975). «Проблемы и результаты о конечных и бесконечных графах». Последние достижения в теории графов (Материалы второго чехословацкого симпозиума, Прага, 1974) . Академия, Прага. стр. 183–192.
33. Эрдеш, Пол (1984). «О некоторых проблемах теории графов, комбинаторного анализа и комбинаторной теории чисел» (PDF) . Теория графов и комбинаторика : 1–17.
34. Кохаякава, Ю.; Премель, Х.Ю.; Рёдль, В. (1998). «Индуцированные числа Рамсея» (PDF) . Комбинаторика . 18 (3): 373–404. дои : 10.1007/PL00009828 .
35. Фокс, Джейкоб ; Судаков, Бенни (2008). «Индуцированные теоремы типа Рамсея». Достижения в математике . 219 (6): 1771–1800. arXiv : 0706.4112 . дои : 10.1016/j.aim.2008.07.009 .
36. Конлон, Дэвид ; Фокс, Джейкоб ; Судаков, Бенни (2012). «О двух задачах теории графов Рэмсея». Комбинаторика . 32 (5): 513–535. arXiv : 1002.0045 . дои : 10.1007/s00493-012-2710-3 .
37. Бек, Йожеф (1990). «О размере числа путей, деревьев и цепей Рамсея. II». В Нешетриле, Дж.; Рёдль, В. (ред.). Математика теории Рамсея . Алгоритмы и комбинаторика. Том. 5. Шпрингер, Берлин, Гейдельберг. стр. 34–45. дои : 10.1007/978-3-642-72905-8_4 . ISBN 978-3-642-72907-2.
38. Лучак, Томаш; Рёдль, Войтех (март 1996 г.). «О индуцированных числах Рамсея для графов с ограниченной максимальной степенью». Журнал комбинаторной теории . Серия Б. 66 (2): 324–333. дои : 10.1006/jctb.1996.0025 .
39. Конлон, Дэвид ; Фокс, Джейкоб ; Чжао, Юфэй (май 2014 г.). «Экстремальные результаты в разреженных псевдослучайных графах». Достижения в математике . 256 : 206–29. arXiv : 1204.6645 . дои : 10.1016/j.aim.2013.12.004 .
40. Фокс, Джейкоб ; Судаков, Бенни (2009). «Теоремы плотности для двудольных графов и связанные с ними результаты типа Рамсея». Комбинаторика . 29 (2): 153–196. arXiv : 0707.4159v2 . дои : 10.1007/s00493-009-2475-5 .
41. Конлон, Дэвид ; Делламоника-младший, Домингос; Ла Флер, Стивен; Рёдль, Войтех ; Шахт, Матиас (2017). «Заметка о индуцированных числах Рамсея». В Лебле, Мартин; Нешетржил, Ярослав ; Томас, Робин (ред.). Путешествие по дискретной математике . Спрингер, Чам. стр. 357–366. arXiv : 1601.01493 . дои : 10.1007/978-3-319-44479-6_13 . ISBN 978-3-319-44478-9.
42. Мартин Гулд. «Теория Рэмси» (PDF) .
43. Душник, Бен; Миллер, EW (1941). «Частично заказанные наборы». Американский журнал математики . 63 (3): 600–610. дои : 10.2307/2371374. hdl : 10338.dmlcz/100377 . JSTOR  2371374. MR  0004862.. См., в частности, теоремы 5.22 и 5.23.
44. Дистель, Рейнхард (2010). «Глава 8, Бесконечные графы». Теория графов (4-е изд.). Гейдельберг: Springer-Verlag. С. 209–2010. ISBN 978-3-662-53621-6.
45. Маккей, Брендан Д.; Радзишовский, Станислав П. (1991). «Вычислено первое классическое число Рамсея для гиперграфов». Материалы второго ежегодного симпозиума ACM-SIAM по дискретным алгоритмам, SODA'91 : 304–308.
46. Дыбизбанский, Януш (31 декабря 2018 г.). «Нижняя оценка числа Рамсея гиперграфа R (4,5;3)». Вклад в дискретную математику . 13 (2). дои : 10.11575/cdm.v13i2.62416 . ISSN  1715-0868.
47. Смит, Уоррен Д.; Эксу, Джефф, Частичный ответ на головоломку № 27: количество, подобное Рэмси , получено 2 июня 2020 г.
48. Нейман, Дэвид; Макки, Джон; Хойле, Марин (01.11.2020). «Более жесткие границы направленного числа Рэмси R (7)». arXiv : 2011.00683 [math.CO].
49. Хиршфельдт, Денис Р. (2014). Нарезка правды . Серия конспектов лекций Института математических наук Национального университета Сингапура. Том. 28. Всемирная научная.
50. Бласс, Андреас (сентябрь 1977 г.). «Теорема Рэмси в иерархии принципов выбора». Журнал символической логики . 42 (3): 387–390. дои : 10.2307/2272866. ISSN  1943-5886.
51. Форстер, TE; Трасс, Дж. К. (январь 2007 г.). «Теорема Рэмсея и лемма Кенига». Архив математической логики . 46 (1): 37–42. doi : 10.1007/s00153-006-0025-z. ISSN  1432-0665.

Рекомендации

• Айтаи, Миклош ; Комлос, Янош ; Семереди, Эндре (1980), «Заметки о числах Рамсея», Дж. Комбин. Теория Сер. А , 29 (3): 354–360, doi : 10.1016/0097-3165(80)90030-8.
• Боман, Том; Киваш, Питер (2010), «Ранняя эволюция процесса без H», Invent. Математика. , 181 (2): 291–336, arXiv : 0908.0429 , Bibcode : 2010InMat.181..291B, doi : 10.1007/s00222-010-0247-x, S2CID  2429894
• Бруальди, Ричард А. (2010), Вводная комбинаторика (5-е изд.), Prentice-Hall, стр. 77–82, ISBN 978-0-13-602040-0
• Конлон, Дэвид (2009), «Новая верхняя граница диагональных чисел Рамсея», Annals of Mathematics , 170 (2): 941–960, arXiv : math/0607788v1 , doi : 10.4007/annals.2009.170.941, MR  2552114, S2CID  9238219.
• Эрдеш, Пол (1947), «Некоторые замечания по теории графов», Bull. амер. Математика. Соц. , 53 (4): 292–294, doi : 10.1090/S0002-9904-1947-08785-1.
• Эрдеш, П .; Мозер, Л. (1964), «О представлении ориентированных графов как объединений порядков» (PDF) , A Magyar Tudományos Akadémia, Matematikai Kutató Intézetének Közleményei , 9 : 125–132, MR  0168494
• Эрдеш, Пол ; Секерес, Джордж (1935), «Комбинаторная задача в геометрии» (PDF) , Compositio Mathematica , 2 : 463–470, doi : 10.1007/978-0-8176-4842-8_3, ISBN 978-0-8176-4841-1.
• Эксу, Г. (1989), «Нижняя оценка для R(5,5)», Journal of Graph Theory , 13 : 97–98, doi : 10.1002/jgt.3190130113.
• Грэм, Р .; Ротшильд, Б.; Спенсер, Дж. Х. (1990), Теория Рэмси , Нью-Йорк: Джон Уайли и сыновья..
• Гросс, Джонатан Л. (2008), Комбинаторные методы с компьютерными приложениями , CRC Press, стр. 458, ISBN 978-1-58488-743-0
• Харари, Фрэнк (1972), Теория графов , Аддисон-Уэсли, стр. 16–17, ISBN 0-201-02787-9
• Рэмси, Ф. П. (1930), «К проблеме формальной логики», Труды Лондонского математического общества , 30 : 264–286, doi : 10.1112/plms/s2-30.1.264.
• Спенсер, Дж. (1975), «Теорема Рэмси - новая нижняя оценка», Дж. Комбин. Теория Сер. А , 18 : 108–115, дои : 10.1016/0097-3165(75)90071-0.
• Бянь, Чжэнбин; Чудак, Фабиан; Макриди, Уильям Г.; Кларк, Лейн; Гайтан, Франк (2013), «Экспериментальное определение чисел Рамсея», Physical Review Letters , 111 (13): 130505, arXiv : 1201.1842 , Бибкод : 2013PhRvL.111m0505B, doi : 10.1103/PhysRevLett.111.130505, PMID  24116761, S2CID  1303361.

Внешние ссылки

• «Теорема Рэмси», Математическая энциклопедия , EMS Press , 2001 [1994]
• Ramsey@Home — это проект распределенных вычислений , предназначенный для поиска новых нижних границ различных чисел Рамсея с использованием множества различных методов.
• Динамический обзор малых чисел Рамсея в Электронном журнале комбинаторики (Станислав Радзишовский)
• Число Рамсея - из MathWorld (содержит нижнюю и верхнюю границы до R (19, 19))
• Число Рэмси – Джеффри Эксу (содержит R(5, 5) > 42, контрдоказательство)