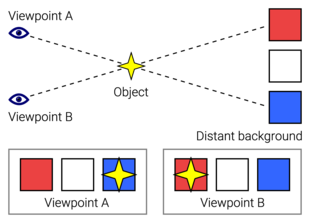
Параллакс — это смещение или разница в видимом положении объекта, наблюдаемого вдоль двух различных линий зрения , и измеряется углом или полууглом наклона между этими двумя линиями. [1] [2] Из -за ракурса близлежащие объекты показывают больший параллакс, чем дальние объекты, поэтому параллакс можно использовать для определения расстояний.
Для измерения больших расстояний, таких как расстояние от планеты или звезды до Земли , астрономы используют принцип параллакса. Здесь термин параллакс — это полуугол наклона между двумя линиями визирования на звезду, наблюдаемый, когда Земля находится по разные стороны от Солнца на своей орбите. [a] Эти расстояния образуют низшую ступеньку того, что называется « космической лестницей расстояний », первой в последовательности методов, с помощью которых астрономы определяют расстояния до небесных объектов, служащих основой для других измерений расстояний в астрономии, образующих высшие ступени лестницы.
Параллакс также влияет на оптические приборы, такие как прицелы, бинокли , микроскопы и двухлинзовые зеркальные камеры , которые видят объекты под немного разными углами. Многие животные, как и люди, имеют два глаза с перекрывающимися полями зрения , которые используют параллакс для получения восприятия глубины ; этот процесс известен как стереопсис . В компьютерном зрении эффект используется для компьютерного стереозрения , и существует устройство, называемое дальномером параллакса , которое использует его для определения расстояния, а в некоторых вариантах также высоты до цели.
Простой повседневный пример параллакса можно увидеть на приборных панелях автомобилей, в которых используется механический спидометр со стрелкой . Если смотреть прямо спереди, скорость может показывать ровно 60, но если смотреть с пассажирского сиденья, может показаться, что стрелка показывает немного другую скорость из-за угла обзора в сочетании со смещением стрелки от плоскости числового циферблата.

Поскольку глаза человека и других животных находятся в разных положениях на голове, они одновременно представляют разные виды. Это основа стереопсиса , процесса, посредством которого мозг использует параллакс из-за разных видов глаз, чтобы получить восприятие глубины и оценить расстояния до объектов. [3]
Животные также используют параллакс движения , при котором животные (или только голова) двигаются, чтобы получить разные точки обзора. Например, голуби (чьи глаза не имеют перекрывающихся полей зрения и, таким образом, не могут использовать стереопсис) качают головой вверх и вниз, чтобы увидеть глубину. [4] Параллакс движения также используется в покачивающейся стереоскопии , компьютерной графике, которая обеспечивает подсказки глубины посредством анимации смещения точки обзора, а не посредством бинокулярного зрения.

Параллакс возникает из-за изменения точки зрения, происходящего из-за движения наблюдателя, наблюдаемого или обоих. Существенно относительное движение. Наблюдая параллакс, измеряя углы и используя геометрию , можно определить расстояние .
Измерение расстояния с помощью параллакса является частным случаем принципа триангуляции , который гласит, что можно решить для всех сторон и углов в сети треугольников, если в дополнение ко всем углам в сети была измерена длина хотя бы одной стороны. Таким образом, тщательное измерение длины одной базовой линии может зафиксировать масштаб всей сети триангуляции. В параллаксе треугольник чрезвычайно длинный и узкий, и путем измерения как его самой короткой стороны (движение наблюдателя), так и малого верхнего угла (всегда меньше 1 угловой секунды , [5] оставляя два других близкими к 90 градусам) можно определить длину длинных сторон (на практике считающихся равными).
В астрономии, предполагая, что угол мал, расстояние до звезды (измеряемое в парсеках ) является обратной величиной параллакса (измеряемого в угловых секундах ): Например, расстояние до Проксимы Центавра составляет 1/0,7687 = 1,3009 парсека (4,243 световых лет). [6]
На Земле для определения расстояния до цели можно использовать дальномер совпадения или дальномер параллакса. В геодезии задача обратной засечки исследует угловые измерения от известной базовой линии для определения координат неизвестной точки.
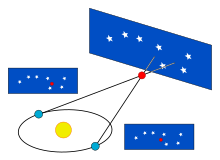
Наиболее важные фундаментальные измерения расстояний в астрономии происходят из тригонометрического параллакса, применяемого в методе звездного параллакса . По мере того, как Земля вращается вокруг Солнца, положение близлежащих звезд будет казаться слегка смещенным относительно более удаленного фона. Эти смещения представляют собой углы в равнобедренном треугольнике , где 2 а.е. (расстояние между крайними положениями орбиты Земли вокруг Солнца) составляют основание треугольника, а расстояние до звезды — длинные равные по длине стороны. Величина смещения довольно мала, даже для ближайших звезд, составляя 1 угловую секунду для объекта на расстоянии 1 парсека (3,26 световых года ), и затем уменьшается в угловой величине по мере увеличения расстояния. Астрономы обычно выражают расстояния в единицах парсеков (параллаксных угловых секунд); в популярных средствах массовой информации используются световые годы.
Поскольку параллакс становится меньше с увеличением расстояния до звезды, полезные расстояния могут быть измерены только для звезд, которые находятся достаточно близко, чтобы иметь параллакс, превышающий точность измерения более чем в несколько раз. Например, в 1990-х годах миссия Hipparcos получила параллаксы для более чем сотни тысяч звезд с точностью около миллисекунды дуги , [7] предоставляя полезные расстояния для звезд до нескольких сотен парсеков. Широкоугольная камера 3 космического телескопа Хаббл имеет потенциал для обеспечения точности от 20 до 40 микросекунд дуги, что позволяет проводить надежные измерения расстояний до 5000 парсеков (16000 световых лет) для небольшого количества звезд. [8] [9] Космическая миссия Gaia предоставила аналогичные точные расстояния для большинства звезд ярче 15-й величины. [10]
Расстояния можно измерить в пределах 10% до Галактического центра , примерно в 30 000 световых лет. Звезды имеют скорость относительно Солнца, которая вызывает собственное движение (поперечное по небу) и радиальную скорость (движение к Солнцу или от Солнца). Первая определяется путем построения графика изменения положения звезд в течение многих лет, в то время как последняя получается путем измерения доплеровского смещения спектра звезды, вызванного движением вдоль луча зрения. Для группы звезд с одинаковым спектральным классом и схожим диапазоном звездных величин средний параллакс может быть выведен из статистического анализа собственных движений относительно их радиальных скоростей. Этот статистический метод параллакса полезен для измерения расстояний ярких звезд за пределами 50 парсек и гигантских переменных звезд , включая цефеиды и переменные типа RR Лиры . [11]


Движение Солнца через пространство обеспечивает более длинную базовую линию, которая увеличит точность измерений параллакса, известного как вековой параллакс . Для звезд в диске Млечного Пути это соответствует средней базовой линии в 4 а.е. в год, в то время как для звезд гало базовая линия составляет 40 а.е. в год. Через несколько десятилетий базовая линия может быть на порядки больше базовой линии Земля-Солнце, используемой для традиционного параллакса. Однако вековой параллакс вносит более высокий уровень неопределенности, поскольку относительная скорость наблюдаемых звезд является дополнительной неизвестной. При применении к выборкам из нескольких звезд неопределенность может быть уменьшена; неопределенность обратно пропорциональна квадратному корню размера выборки. [14]
Движущийся параллакс скопления — это метод, при котором движения отдельных звезд в соседнем звездном скоплении могут быть использованы для определения расстояния до скопления. Только рассеянные скопления находятся достаточно близко, чтобы этот метод был полезен. В частности, расстояние, полученное для Гиад, исторически было важным шагом в лестнице расстояний.
Для других отдельных объектов могут быть сделаны фундаментальные оценки расстояния при особых обстоятельствах. Если расширение газового облака, например остатка сверхновой или планетарной туманности , можно наблюдать с течением времени, то можно оценить расстояние параллакса расширения до этого облака. Однако эти измерения страдают от неопределенностей в отклонении объекта от сферичности. Расстояние до двойных звезд , которые являются как визуальными , так и спектроскопическими двойными, также можно оценить аналогичными способами, и они не страдают от вышеуказанной геометрической неопределенности. Общей характеристикой этих методов является то, что измерение углового движения сочетается с измерением абсолютной скорости (обычно получаемой с помощью эффекта Доплера ). Оценка расстояния происходит из вычисления того, насколько далеко должен находиться объект, чтобы его наблюдаемая абсолютная скорость отображалась вместе с наблюдаемым угловым движением.
В частности, параллаксы расширения могут дать фундаментальные оценки расстояний для очень далеких объектов, поскольку выбросы сверхновых имеют большие скорости расширения и большие размеры (по сравнению со звездами). Кроме того, их можно наблюдать с помощью радиоинтерферометров , которые могут измерять очень малые угловые движения. Они объединяются, чтобы дать фундаментальные оценки расстояний до сверхновых в других галактиках. [15] Хотя такие случаи и ценны, они довольно редки, поэтому они служат важными проверками согласованности на лестнице расстояний, а не рабочими лошадками сами по себе.Измерения, выполненные путем просмотра положения некоторого маркера относительно чего-либо, что должно быть измерено, подвержены ошибке параллакса, если маркер находится на некотором расстоянии от объекта измерения и не рассматривается с правильной позиции. Например, если измерять расстояние между двумя делениями на линии с помощью линейки, нанесенной на ее верхнюю поверхность, толщина линейки отделит ее отметки от делений. Если смотреть с позиции, не точно перпендикулярной линейке, видимое положение сместится, и показания будут менее точными, чем способна дать линейка.
Аналогичная ошибка возникает при считывании положения указателя по шкале в таком приборе, как аналоговый мультиметр . Чтобы помочь пользователю избежать этой проблемы, шкала иногда печатается над узкой полоской зеркала , а глаз пользователя располагается так, что указатель заслоняет его отражение, гарантируя, что линия взгляда пользователя перпендикулярна зеркалу и, следовательно, шкале. Тот же эффект изменяет скорость, считываемую на спидометре автомобиля водителем перед ним и пассажиром сбоку, значения считываются с сетки , не находясь в реальном контакте с дисплеем осциллографа и т. д.
При просмотре через стереопросмотрщик пара аэрофотоснимков дает выраженный стереоэффект ландшафта и зданий. Высокие здания кажутся «перевернутыми» в направлении от центра фотографии. Измерения этого параллакса используются для определения высоты зданий, при условии, что известны высота полета и базовые расстояния. Это ключевой компонент процесса фотограмметрии .
Ошибку параллакса можно увидеть при съемке фотографий многими типами камер, такими как двухобъективные зеркальные камеры и камеры с видоискателями (например, дальномерные камеры ). В таких камерах глаз видит объект через другую оптику (видоискатель или второй объектив), чем тот, через который делается фотография. Поскольку видоискатель часто находится над объективом камеры, фотографии с ошибкой параллакса часто оказываются немного ниже, чем предполагалось, классическим примером является изображение человека с обрезанной головой. Эта проблема решается в однообъективных зеркальных камерах , в которых видоискатель видит через тот же объектив, через который делается фотография (с помощью подвижного зеркала), что позволяет избежать ошибки параллакса.
Параллакс также является проблемой при сшивке изображений , например, панорам.
Параллакс влияет на прицельные приспособления дальнобойного оружия многими способами. На прицелах, установленных на стрелковом оружии и луках и т. д., перпендикулярное расстояние между прицелом и осью запуска оружия (например, осью канала ствола ружья) — обычно называемое « высотой прицела » — может вызывать значительные ошибки прицеливания при стрельбе на близком расстоянии, особенно при стрельбе по небольшим целям. [16] Эта ошибка параллакса компенсируется (при необходимости) с помощью расчетов, которые также учитывают другие переменные, такие как падение пули , поправку на ветер и ожидаемое расстояние до цели. [17] Высота прицела может быть использована с выгодой при «пристрелке» винтовок для полевого использования. Типичная охотничья винтовка (.222 с оптическим прицелом), пристрелянная на 75 м, будет по-прежнему полезна на расстоянии от 50 до 200 м (от 55 до 219 ярдов) без необходимости дальнейшей регулировки. [ требуется цитата ]
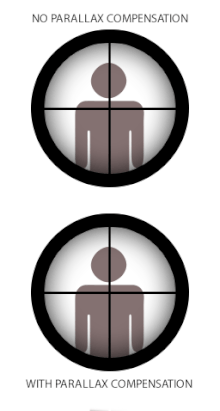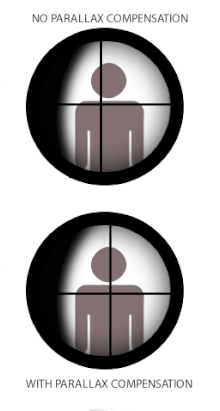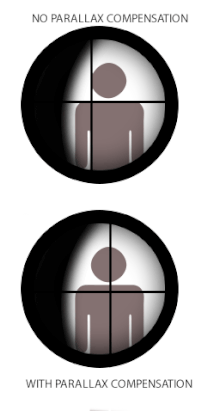
В некоторых сеточных оптических приборах, таких как телескопы , микроскопы или телескопические прицелы («прицелы»), используемые на стрелковом оружии и теодолитах , параллакс может создавать проблемы, когда сетка не совпадает с фокальной плоскостью изображения цели. Это происходит потому, что когда сетка и цель не находятся в одном фокусе, оптически соответствующие расстояния, проецируемые через окуляр, также различаются, и глаз пользователя будет регистрировать разницу в параллаксах между сеткой и целью (всякий раз, когда меняется положение глаза) как относительное смещение друг над другом. Термин « сдвиг параллакса» относится к результирующим кажущимся «плавающим» движениям сетки по изображению цели, когда пользователь перемещает свою голову/глаз вбок (вверх/вниз или влево/вправо) за прицелом, [18] т. е. ошибка, при которой сетка не остается выровненной с оптической осью пользователя .
Некоторые прицелы для огнестрельного оружия оснащены механизмом компенсации параллакса, который состоит из подвижного оптического элемента, который позволяет оптической системе смещать фокус изображения цели на различных расстояниях в ту же оптическую плоскость сетки (или наоборот). Многие низкоуровневые телескопические прицелы могут не иметь компенсации параллакса, поскольку на практике они все равно могут работать очень приемлемо без устранения смещения параллакса. В этом случае прицел часто устанавливается на указанное расстояние без параллакса, которое наилучшим образом соответствует их предполагаемому использованию. Типичные стандартные заводские расстояния без параллакса для охотничьих прицелов составляют 100 ярдов (или 90 м), что делает их подходящими для охотничьих выстрелов, которые редко превышают 300 ярдов/м. Некоторые спортивные и военные прицелы без компенсации параллакса могут быть настроены на расстояние без параллакса до 300 ярдов/м, чтобы сделать их более подходящими для прицеливания на большие расстояния. [ необходима цитата ] Прицелы для оружия с более короткими практическими дальностями, такие как пневматическое оружие , винтовки с кольцевым воспламенением , дробовики и дульнозарядные ружья , будут иметь настройки параллакса для более коротких расстояний, обычно 50 м (55 ярдов) для прицелов с кольцевым воспламенением и 100 м (110 ярдов) для дробовиков и дульнозарядных ружей. [ необходима цитата ] Прицелы для пневматического оружия очень часто встречаются с регулируемым параллаксом, обычно в виде конструкции с регулируемым объективом (или «AO» для краткости), и могут регулироваться вплоть до 3 метров (3,3 ярда). [ необходима цитата ]
Неувеличивающие рефлекторные или «рефлекторные» прицелы теоретически могут быть «свободны от параллакса». Но поскольку эти прицелы используют параллельный коллимированный свет, это справедливо только тогда, когда цель находится на бесконечности. На конечных расстояниях движение глаза перпендикулярно устройству вызовет движение параллакса в изображении сетки в точном соответствии с положением глаза в цилиндрическом столбе света, создаваемом коллимирующей оптикой. [19] [20] Прицелы огнестрельного оружия, такие как некоторые коллиматорные прицелы , пытаются исправить это, не фокусируя сетку на бесконечности, а вместо этого на некотором конечном расстоянии, расчетном целевом диапазоне, где сетка будет показывать очень мало движения из-за параллакса. [19] Некоторые производители продают модели рефлекторных прицелов, которые они называют «свободными от параллакса», [21] но это относится к оптической системе, которая компенсирует внеосевую сферическую аберрацию , оптическую ошибку, вызванную сферическим зеркалом, используемым в прицеле, которая может привести к отклонению положения сетки от оптической оси прицела при изменении положения глаза. [22] [23]
Из-за расположения орудий полевой или морской артиллерии каждое из них имеет немного иную перспективу цели относительно расположения самой системы управления огнем . Поэтому при наведении своих орудий на цель система управления огнем должна компенсировать параллакс, чтобы гарантировать, что огонь из каждого орудия будет сходиться на цели.
Несколько скульптурных работ Марка Ренна играют с параллаксом, кажущимися абстрактными, пока не увидишь их под определенным углом. Одна из таких скульптур — Дарвиновские ворота (на фото) в Шрусбери , Англия, которые под определенным углом, по словам Historic England , образуют купол в «форме саксонского шлема с нормандским окном... вдохновленный чертами церкви Святой Марии, которую посещал Чарльз Дарвин в детстве». [24]
В философском/геометрическом смысле: кажущееся изменение направления объекта, вызванное изменением позиции наблюдения, которое обеспечивает новую линию зрения. Видимое смещение или различие положения объекта, как видно с двух разных станций или точек зрения. В современной литературе параллакс также может быть той же историей или похожей историей примерно из той же временной шкалы, из одной книги, рассказанной с другой точки зрения в другой книге. Слово и концепция занимают видное место в романе Джеймса Джойса 1922 года «Улисс» . Орсон Скотт Кард также использовал этот термин, ссылаясь на «Тень Эндера» по сравнению с «Игрой Эндера» .
Метафору использовал словенский философ Славой Жижек в своей книге 2006 года «Параллаксный вид », заимствовав концепцию «параллаксного вида» у японского философа и литературного критика Кодзина Каратани . Жижек отмечает
Философский поворот, который следует добавить (к параллаксу), конечно, заключается в том, что наблюдаемое расстояние не просто «субъективно», поскольку один и тот же объект, который существует «там», виден с двух разных позиций или точек зрения. Скорее, как сказал бы Гегель , субъект и объект по своей сути «опосредованы», так что « эпистемологический » сдвиг в точке зрения субъекта всегда отражает « онтологический » сдвиг в самом объекте. Или — выражаясь языком Лакана — взгляд субъекта всегда уже вписан в сам воспринимаемый объект, под видом его «слепого пятна», того, что «в объекте больше, чем сам объект», точки, из которой сам объект возвращает взгляд. «Конечно, картина у меня в глазах, но я также на картине»… [25]
- Славой Жижек, Параллакс
Взаимный наклон двух линий, пересекающихся под углом.
Астрон.
Видимое смещение или разница в видимом положении объекта, вызванное фактическим изменением (или разницей) положения точки наблюдения; спец. угловая величина такого смещения или разницы положения, представляющая собой угол, заключенный между двумя прямыми линиями, проведенными к объекту с двух разных точек зрения и представляющий собой меру расстояния до объекта.
{{cite web}}: CS1 maint: числовые имена: список авторов ( ссылка )