Комплексный многогранник

В геометрии комплексный многогранник — это обобщение многогранника в действительном пространстве до аналогичной структуры в комплексном гильбертовом пространстве , где каждому действительному измерению соответствует мнимое .

Сложный многогранник можно понимать как совокупность сложных точек, прямых, плоскостей и т. д., где каждая точка является стыком нескольких прямых, каждая прямая — нескольких плоскостей и т. д.

Точные определения существуют только для правильных комплексных многогранников, которые являются конфигурациями . Правильные комплексные многогранники были полностью охарактеризованы и могут быть описаны с помощью символической нотации, разработанной Коксетером .

Были также описаны некоторые сложные многогранники, которые не являются полностью правильными.

Определения и введение

Комплексная линия имеет одно измерение с действительными координатами и другое с мнимыми координатами. Говорят, что применение действительных координат к обоим измерениям дает ей два измерения над действительными числами. Действительная плоскость с мнимой осью, обозначенной как таковая, называется диаграммой Аргана . Из-за этого ее иногда называют комплексной плоскостью. Комплексное 2-пространство (также иногда называемое комплексной плоскостью) является, таким образом, четырехмерным пространством над действительными числами, и так далее в более высоких измерениях. ${\displaystyle \mathbb {C} ^{1}}$

Комплексный n -политоп в комплексном n -пространстве является аналогом действительного n -политопа в действительном n -пространстве. Однако не существует естественного комплексного аналога упорядочения точек на действительной прямой (или связанных с ним комбинаторных свойств). Из-за этого комплексный политоп не может рассматриваться как смежная поверхность, и он не ограничивает внутреннюю часть так, как это делает действительный политоп.

В случае правильных многогранников точное определение можно дать, используя понятие симметрии. Для любого правильного многогранника группа симметрии (здесь — комплексная группа отражений , называемая группой Шепарда ) действует транзитивно на флагах , то есть на вложенных последовательностях точки, содержащейся в прямой, содержащейся в плоскости, и так далее.

Более полно можно сказать, что набор P аффинных подпространств (или плоскостей ) комплексного унитарного пространства V размерности n является правильным комплексным многогранником, если он удовлетворяет следующим условиям: ^{[1] [2]}

• для каждого −1 ≤ i < j < k ≤ n , если F является квартирой в P размерности i и H является квартирой в P размерности k такой, что F ⊂ H , то существует по крайней мере две квартиры G в P размерности j такие, что F ⊂ G ⊂ H ;
• для каждого i , j такого, что −1 ≤ i < j − 2, j ≤ n , если F ⊂ G являются плоскостями P размерностей i , j , то множество плоскостей между F и G связно в том смысле, что можно получить от любого члена этого множества к любому другому с помощью последовательности включений; и
• подмножество унитарных преобразований V , которые фиксируют P, транзитивны на флагах F ₀ ⊂ F ₁ ⊂ … ⊂ F _n плоскостей P (с F _i размерности i для всех i ).

(Здесь под плоскостью размерности −1 понимается пустое множество.) Таким образом, по определению, правильные комплексные многогранники являются конфигурациями в комплексном унитарном пространстве.

Правильные комплексные многогранники были открыты Шепардом (1952), а теория была далее развита Кокстером (1974).

Комплексный многогранник существует в комплексном пространстве эквивалентной размерности. Например, вершины комплексного многоугольника являются точками в комплексной плоскости (плоскости, в которой каждая точка имеет два комплексных числа в качестве своих координат, не путать с плоскостью Аргана комплексных чисел), а ребра являются комплексными линиями, существующими как (аффинные) подпространства плоскости и пересекающимися в вершинах. Таким образом, как одномерному комплексному пространству, ребру может быть задана собственная система координат, в которой каждая точка ребра представлена ​​одним комплексным числом. ${\displaystyle \mathbb {C} ^{2}}$ ${\displaystyle \mathbb {C} ^{1}}$

В правильном комплексном многограннике вершины, инцидентные ребру, расположены симметрично относительно их центроида , который часто используется в качестве начала системы координат ребра (в реальном случае центроид — это просто середина ребра). Симметрия возникает из-за комплексного отражения относительно центроида; это отражение оставит величину любой вершины неизменной, но изменит ее аргумент на фиксированную величину, перемещая его к координатам следующей вершины по порядку. Поэтому мы можем предположить (после подходящего выбора масштаба), что вершины на ребре удовлетворяют уравнению, где p — число инцидентных вершин. Таким образом, на диаграмме Аргана ребра вершинные точки лежат в вершинах правильного многоугольника с центром в начале координат. ${\displaystyle x^{p}-1=0}$

Выше показаны три действительные проекции правильного комплексного многоугольника 4{4}2 с ребрами a, b, c, d, e, f, g, h . Он имеет 16 вершин, которые для ясности не были помечены индивидуально. Каждое ребро имеет четыре вершины, и каждая вершина лежит на двух ребрах, следовательно, каждое ребро встречается с четырьмя другими ребрами. На первой диаграмме каждое ребро представлено квадратом. Стороны квадрата не являются частями многоугольника, а нарисованы исключительно для того, чтобы помочь визуально связать четыре вершины. Ребра расположены симметрично. (Обратите внимание, что диаграмма выглядит похожей на проекцию плоскости Коксетера B 4 тессеракта , но структурно отличается).

Средняя диаграмма отказывается от восьмиугольной симметрии в пользу ясности. Каждое ребро показано как реальная линия, а каждая точка пересечения двух линий является вершиной. Связность между различными ребрами очевидна.

Последняя диаграмма дает представление о структуре, спроецированной в трех измерениях: два куба вершин на самом деле имеют одинаковый размер, но видны в перспективе на разных расстояниях в четвертом измерении.

Правильные комплексные одномерные многогранники

Комплексные 1-многогранники, представленные на плоскости Аргана как правильные многоугольники для p = 2, 3, 4, 5 и 6, с черными вершинами. Центроид вершин p показан красным. Стороны многоугольников представляют одно применение генератора симметрии, отображающее каждую вершину в следующую копию против часовой стрелки. Эти многоугольные стороны не являются ребрами многогранника, поскольку комплексный 1-многогранник может не иметь ребер (он часто является комплексным ребром) и содержит только вершинные элементы.

Действительный одномерный многогранник существует как замкнутый сегмент в действительной прямой , определяемый двумя его конечными точками или вершинами в прямой. Его символ Шлефли — {} . ${\displaystyle \mathbb {R} ^{1}}$

Аналогично, комплексный 1-многогранник существует как набор p вершинных точек на комплексной прямой . Они могут быть представлены как набор точек на диаграмме Аргана ( x , y )= x + iy . Правильный комплексный 1-мерный многогранник _p {} имеет p ( p ≥ 2) вершинных точек, расположенных так, чтобы сформировать выпуклый правильный многоугольник { p } на плоскости Аргана. ^[4] ${\displaystyle \mathbb {C} ^{1}}$

В отличие от точек на действительной прямой, точки на комплексной прямой не имеют естественного порядка. Таким образом, в отличие от действительных многогранников, нельзя определить внутреннюю часть. ^[5] Несмотря на это, комплексные 1-многогранники часто рисуются, как здесь, как ограниченный правильный многоугольник на плоскости Аргана.

Реальное ребро генерируется как линия между точкой и ее отраженным изображением через зеркало. Унитарный порядок отражения 2 можно рассматривать как поворот на 180 градусов вокруг центра. Ребро неактивно, если точка генератора находится на отражающей линии или в центре.

Правильный действительный одномерный многогранник представляется пустым символом Шлефли {} или диаграммой Коксетера-Дынкина . Точка или узел диаграммы Коксетера-Дынкина представляет собой генератор отражения, тогда как окружность вокруг узла означает, что точка генератора не находится на отражении, поэтому ее отражающее изображение является отличной от него точкой. В более широком смысле, правильный комплексный одномерный многогранник в имеет диаграмму Коксетера-Дынкина ${\displaystyle \mathbb {C} ^{1}}$ , для любого положительного целого числа p , 2 или больше, содержащего p вершин. p может быть подавлено, если оно равно 2. Его также можно представить пустым символом Шлефли _p {}, } _p {, {} _p или _p {2} ₁ . 1 — это нотационный заполнитель, представляющий несуществующее отражение или генератор тождества периода 1. (0-многогранник, действительный или комплексный, является точкой и представляется как } { или ₁ {2} ₁ .)

Симметрия обозначается диаграммой Кокстера , и может быть альтернативно описана в обозначениях Кокстера как _p [], [] _p или ] _p [, _p [2] ₁ или _p [1] _p . Симметрия изоморфна циклической группе , порядка p . ^[6] Подгруппы _p [] являются любыми целыми делителями d , _d [], где d ≥2.

Генератор унитарного оператора длярассматривается как вращение на 2π/ p радиан против часовой стрелки , аребро создается путем последовательного применения одного унитарного отражения. Генератор унитарного отражения для 1-политопа с p вершинами — это e ^{2π i / p} = cos(2π/ p ) + i sin(2π/ p ) . Когда p = 2, генератор — это e ^{π i} = –1, то же самое, что и точечное отражение в действительной плоскости.

В более сложных многогранниках 1-многогранники образуют p -рёбра. 2-рёбро похоже на обычное вещественное ребро тем, что содержит две вершины, но не обязательно должно находиться на вещественной прямой.

Правильные сложные многоугольники

В то время как 1-многогранники могут иметь неограниченное число p , конечные правильные комплексные многоугольники, за исключением многоугольников двойной призмы _p {4} ₂ , ограничены элементами с 5 ребрами (пятиугольными ребрами), а бесконечные правильные апейрогоны также включают элементы с 6 ребрами (шестиугольными ребрами).

Обозначения

Модифицированная нотация Шлефли Шепарда

Шепард изначально разработал модифицированную форму обозначения Шлефли для правильных многогранников. Для многоугольника, ограниченного p ₁ -ребрами, с p ₂ -множеством в качестве вершинной фигуры и общей группой симметрии порядка g , мы обозначаем многоугольник как p ₁ ( g ) p ₂ .

Тогда число вершин V _равно g / p2 _, а число ребер E равно g / p1 .

Сложный многоугольник, показанный выше, имеет восемь квадратных ребер ( p ₁ =4) и шестнадцать вершин ( p ₂ =2). Из этого мы можем вывести, что g = 32, что дает модифицированный символ Шлефли 4(32)2.

Пересмотренная модифицированная нотация Шлефли Коксетера

Более современная нотация _{p 1} { q } _{p 2} принадлежит Кокстеру [ 7 ^] и основана на теории групп. Как группа симметрии, ее символ — _{p 1} [ q ] _{p 2} .

Группа симметрии _{p 1} [ q ] _{p 2} представлена ​​2 генераторами R ₁ , R ₂ , где: R ₁ ^{p ₁} = R ₂ ^{p ₂} = I. Если q четное, (R ₂ R ₁ ) ^{q /2} = (R ₁ R ₂ ) ^{q /2} . Если q нечетное, (R ₂ R ₁ ) ^(q−1)/2 R ₂ = (R ₁ R ₂ ) ^{( q −1)/2} R ₁ . Когда q нечетное, p ₁ = p ₂ .

Для ₄ [4] ₂ имеет R ₁ ⁴ = R ₂ ² = I, (R ₂ R ₁ ) ² = (R ₁ R ₂ ) ² .

Для ₃ [5] ₃ имеет R ₁ ³ = R ₂ ³ = I, (R ₂ R ₁ ) ² R ₂ = (R ₁ R ₂ ) ² R ₁ .

Диаграммы Коксетера-Дынкина

Коксетер также обобщил использование диаграмм Коксетера-Дынкина на комплексные многогранники, например, комплексный многоугольник _p { q } _r представлен каки эквивалентная группа симметрии, _p [ q ] _r , является диаграммой без колец. Узлы p и r представляют зеркала, создающие p и r изображения на плоскости. Непомеченные узлы на диаграмме имеют неявные 2 метки. Например, действительный правильный многоугольник — это ₂ { q } ₂ или { q } или.

Одно ограничение: узлы, соединенные нечетными порядками ветвей, должны иметь идентичные порядки узлов. Если нет, группа создаст «звездчатые» полигоны с перекрывающимися элементами. Такиявляются обычными, в то время какзвездный.

12 Неприводимых групп Шепарда

12 неприводимых групп Шепарда с их индексными соотношениями подгрупп. ^[8] Подгруппы индекса 2 связаны посредством удаления действительного отражения:
_p [2 q ] ₂ → _p [ q ] _p , индекс 2.
_p [4] _q → _p [ q ] _p , индекс q .

_p [4] ₂ подгруппы: p=2,3,4...
_p [4] ₂ → [ p ], индекс p
_p [4] ₂ → _p []× _p [], индекс 2

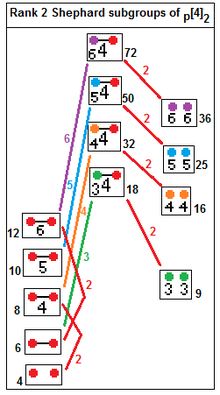
Коксетер перечислил этот список правильных комплексных многоугольников в . Правильный комплексный многоугольник, _p { q } _r или ${\displaystyle \mathbb {C} ^{2}}$, имеет p -рёбер и r -угольные вершинные фигуры . _p { q } _r является конечным многогранником, если ( p + r ) q > pr ( q -2).

Ее симметрия записывается как _p [ q ] _r , называется группой Шепарда , аналогичной группе Кокстера , но также допускающей унитарные отражения .

Для незвездных групп порядок группы _p [ q ] _r можно вычислить как . ^[9] ${\displaystyle g=8/q\cdot (1/p+2/q+1/r-1)^{-2}}$

Число Кокстера для _p [ q ] _r равно , поэтому порядок группы также может быть вычислен как . Правильный комплексный многоугольник можно нарисовать в ортогональной проекции с h -угольной симметрией. ${\displaystyle h=2/(1/p+2/q+1/r-1)}$ ${\displaystyle g=2h^{2}/q}$

Решения ранга 2, генерирующие сложные многоугольники:

Исключенные решения с нечетным q и неравными p и r : ₆ [3] ₂ , ₆ [3] ₃ , ₉ [3] ₃ , ₁₂ [3] ₃ , ..., ₅ [5] ₂ , ₆ [5] ₂ , ₈ [5] ₂ , ₉ [5] ₂ , ₄ [7] ₂ , ₉ [5] ₂ , ₃ [9] ₂ и ₃ [11] ₂ .

Другие целые q с неравными p и r создают звездные группы с перекрывающимися фундаментальными областями:,,,,, и.

Двойственный многоугольник _p { q } _r есть _r { q } _p . Многоугольник вида _p { q } _p является самодвойственным. Группы вида _p [2 q ] ₂ имеют половинную симметрию _p [ q ] _p , поэтому правильный многоугольникто же самое, что и квазирегулярный. Также, правильный многоугольник с теми же порядками узлов,, имеют альтернативную конструкцию, что позволяет соседним ребрам быть двух разных цветов. ^[10]

Порядок группы g используется для вычисления общего числа вершин и ребер. Он будет иметь g / r вершин и g / p ребер. Когда p = r , число вершин и ребер равно. Это условие требуется, когда q нечетно.

Генераторы матриц

Группа p [ q ] r ,, можно представить двумя матрицами: ^[11]

С

к= ${\displaystyle {\sqrt {\frac {cos({\frac {\pi }{p}}-{\frac {\pi }{r}})+cos({\frac {2\pi }{q}})}{2\sin {\frac {\pi }{p}}\sin {\frac {\pi }{r}}}}}}$

Примеры

Перечисление правильных сложных многоугольников

Коксетер перечислил комплексные многоугольники в Таблице III Правильных комплексных многогранников. ^[12]

Визуализации правильных сложных многоугольников

Многоугольники вида _p {2 r } _q можно визуализировать с помощью q цветовых наборов p -ребер. Каждое p -ребро рассматривается как правильный многоугольник, при этом граней нет.

Двумерные ортогональные проекции сложных многоугольников ₂ { r } _q

Многоугольники вида ₂ {4} _q называются обобщенными ортоплексами . Они имеют общие вершины с 4D q - q дуопирамидами , вершины которых соединены 2-ребрами.

• 
  ₂ {4} ₂ ,, с 4 вершинами и 4 ребрами
• 
  ₂ {4} ₃ ,, с 6 вершинами и 9 ребрами ^[13]
• 
  ₂ {4} ₄ ,, с 8 вершинами и 16 ребрами
• 
  ₂ {4} ₅ ,, с 10 вершинами и 25 ребрами
• 
  ₂ {4} ₆ ,, с 12 вершинами и 36 ребрами
• 
  ₂ {4} ₇ ,, с 14 вершинами и 49 ребрами
• 
  ₂ {4} ₈ ,, с 16 вершинами и 64 ребрами
• 
  ₂ {4} ₉ ,, с 18 вершинами и 81 ребром
• 
  ₂ {4} ₁₀ ,, с 20 вершинами и 100 ребрами

Сложные многоугольники _p {4} ₂

Многоугольники вида _p {4} ₂ называются обобщенными гиперкубами (квадратами для многоугольников). Они разделяют вершины с 4D p - p дуопризмами , вершины соединены p-ребрами. Вершины нарисованы зеленым, а p -ребра нарисованы альтернативными цветами, красным и синим. Перспектива слегка искажается для нечетных измерений, чтобы переместить перекрывающиеся вершины из центра.

• 
  ₂ {4} ₂ ,или, с 4 вершинами и 4 2-ребрами
• 
  ₃ {4} ₂ ,или, с 9 вершинами и 6 (треугольными) 3-ребрами ^[13]
• 
  ₄ {4} ₂ ,или, с 16 вершинами и 8 (квадратными) 4-ребрами
• 
  ₅ {4} ₂ ,или, с 25 вершинами и 10 (пятиугольными) 5-ребрами
• 
  ₆ {4} ₂ ,или, с 36 вершинами и 12 (шестиугольными) 6-гранниками
• 
  ₇ {4} ₂ ,или, с 49 вершинами и 14 (семиугольными)7-ребрами
• 
  ₈ {4} ₂ ,или, с 64 вершинами и 16 (восьмиугольными) 8-ребрами
• 
  ₉ {4} ₂ ,или, с 81 вершиной и 18 (девятиугольными) 9-ребрами
• 
  ₁₀ {4} ₂ ,или, со 100 вершинами и 20 (десятиугольными) 10-ребрами

3D перспективные проекции сложных многоугольников _p {4} ₂ . Двойственные ₂ {4} _p

видны путем добавления вершин внутри ребер и добавления ребер вместо вершин.

• 
  ₃ {4} ₂ , илис 9 вершинами, 6 3-ребрами в 2 наборах цветов
• 
  ₂ {4} ₃ ,с 6 вершинами, 9 ребрами в 3 наборах
• 
  ₄ {4} ₂ ,илис 16 вершинами, 8 4-гранниками в 2 наборах цветов и заполненным квадратом с 4 гранями
• 
  ₅ {4} ₂ ,илис 25 вершинами, 10 5-ребрами в 2 наборах цветов

Другие сложные многоугольники _p { r } ₂

• 
  ₃ {6} ₂ ,или, с 24 вершинами черного цвета и 16 3-ребрами, окрашенными в 2 набора 3-ребрьев красного и синего цвета ^[14]
• 
  ₃ {8} ₂ ,или, с 72 вершинами черного цвета и 48 3-ребрами, окрашенными в 2 набора 3-ребрьев красного и синего цветов ^[15]

Двумерные ортогональные проекции сложных многоугольников, _p { r } _p

Многоугольники вида _p { r } _p имеют одинаковое количество вершин и ребер. Они также являются самодвойственными.

• 
  ₃ {3} ₃ ,или, с 8 вершинами черного цвета и 8 3-ребрами, окрашенными в 2 набора 3-ребрьев красного и синего цвета ^[16]
• 
  ₃ {4} ₃ ,или, с 24 вершинами и 24 3-ребрами, показанными в 3 наборах цветов, один набор заполнен ^[17]
• 
  ₄ {3} ₄ ,или, с 24 вершинами и 24 4-ребрами, показанными в 4 наборах цветов ^[17]
• 
  ₃ {5} ₃ ,или, со 120 вершинами и 120 3-ребрами ^[18]
• 
  ₅ {3} ₅ ,или, со 120 вершинами и 120 5-ребрами ^[19]

Правильные комплексные многогранники

В общем случае правильный комплексный многогранник представляется Коксетером как _p { z ₁ } _q {z ₂ } _r {z ₃ } _s ... или диаграмма Коксетера..., имеющий симметрию _p [ z ₁ ] _q [ z ₂ ] _r [ z ₃ ] _s ... или.... ^[20]

Существуют бесконечные семейства правильных комплексных многогранников, которые встречаются во всех измерениях, обобщая гиперкубы и крестовые многогранники в реальном пространстве. «Обобщенный ортотоп» Шепарда обобщает гиперкуб; его символ задается γ^п
_н= _p {4} ₂ {3} ₂ ... ₂ {3} ₂ и диаграмма.... Его группа симметрии имеет диаграмму _p [4] ₂ [3] ₂ ... ₂ [3] ₂ ; в классификации Шепарда–Тодда это группа G( p , 1, n ), обобщающая знаковые матрицы перестановок. Его двойственный регулярный многогранник, «обобщенный крестовый многогранник», представлен символом β^п
_н= ₂ {3} ₂ {3} ₂ ... ₂ {4} _p и диаграмма.... ^[21]

Одномерный правильный комплексный многогранник в представляется как ${\displaystyle \mathbb {C} ^{1}}$, имеющий p вершин, с его действительным представлением в виде правильного многоугольника , { p }. Коксетер также дает ему символ γ^стр
₁или β^стр
₁как одномерный обобщенный гиперкуб или крестовый многогранник. Его симметрия — _p [] или, циклическая группа порядка p . В более высоком многограннике _p {} илипредставляет собой p -образный элемент с 2-образным ребром, {} или, представляющий собой обычное действительное ребро между двумя вершинами. ^[21]

Двойственный комплексный многогранник строится путем обмена k и ( n -1- k )-элементов n -многогранника. Например, двойственный комплексный многогранник имеет вершины, центрированные на каждом ребре, а новые ребра центрируются на старых вершинах. Вершина с v -валентностью создает новое v -ребро, а e -ребра становятся вершинами с e -валентностью. ^[22] Двойственный к правильному комплексному многограннику многогранник имеет перевернутый символ. Правильные комплексные многогранники с симметричными символами, то есть _p { q } _p , _p { q } _r { q } _p , _p { q } _r { s } _r { q } _p и т. д. являются самодвойственными .

Перечисление правильных комплексных многогранников

Некоторые группы Шепарда ранга 3 с их групповыми порядками и рефлексивными отношениями подгрупп

Коксетер перечислил этот список незвездчатых правильных комплексных многогранников в , включая 5 платоновых тел в . ^[23] ${\displaystyle \mathbb {C} ^{3}}$ ${\displaystyle \mathbb {R} ^{3}}$

Правильный комплексный многогранник, _p { n ₁ } _q { n ₂ } _r или, имеетлица,края, и вершинные фигуры .

Для комплексного правильного многогранника _p { n ₁ } _q { n ₂ } _r требуется, чтобы g ₁ = order( _p [ n ₁ ] _q ) и g ₂ = order( _q [ n ₂ ] _r ) были конечными.

Дано g = order( _p [ n ₁ ] _q [ n ₂ ] _r ), число вершин равно g / g ₂ , а число граней равно g / g ₁ . Число ребер равно g / pr .

Визуализации правильных сложных многогранников

Двумерные ортогональные проекции сложных многогранников, _p { s } _t { r } _r

• 
  Реальный {3,3} ,илиимеет 4 вершины, 6 ребер и 4 грани
• 
  ₃ {3} ₃ {3} ₃ ,или, имеет 27 вершин, 72 3-ребра и 27 граней, одна из которых выделена синим цветом. ^[25]
• 
  ₂ {4} ₃ {3} ₃ ,имеет 54 вершины, 216 простых ребер и 72 грани, одна из которых выделена синим цветом. ^[26]
• 
  ₃ {3} ₃ {4} ₂ ,или, имеет 72 вершины, 216 3-ребер и 54 вершины, одна грань выделена синим цветом. ^[27]

Обобщенные октаэдры

Обобщенные октаэдры имеют правильное строениеи квазирегулярная форма как. Все элементы являются симплексами .

• 
  Реальный {3,4} ,или, с 6 вершинами, 12 ребрами и 8 гранями
• 
  ₂ {3} ₂ {4} ₃ ,или, с 9 вершинами, 27 ребрами и 27 гранями
• 
  ₂ {3} ₂ {4} ₄ ,или, с 12 вершинами, 48 ребрами и 64 гранями
• 
  ₂ {3} ₂ {4} ₅ ,или, с 15 вершинами, 75 ребрами и 125 гранями
• 
  ₂ {3} ₂ {4} ₆ ,или, с 18 вершинами, 108 ребрами и 216 гранями
• 
  ₂ {3} ₂ {4} ₇ ,или, с 21 вершиной, 147 ребрами и 343 гранями
• 
  ₂ {3} ₂ {4} ₈ ,или, с 24 вершинами, 192 ребрами и 512 гранями
• 
  ₂ {3} ₂ {4} ₉ ,или, с 27 вершинами, 243 ребрами и 729 гранями
• 
  ₂ {3} ₂ {4} ₁₀ ,или, с 30 вершинами, 300 ребрами и 1000 гранями

Обобщенные кубы

Обобщенные кубы имеют правильную конструкцию, каки призматическая конструкция как, произведение трех p -угольных 1-многогранников. Элементы — обобщенные кубы меньшей размерности.

• 
  Реальный {4,3} ,илиимеет 8 вершин, 12 ребер и 6 граней
• 
  ₃ {4} ₂ {3} ₂ ,илиимеет 27 вершин, 27 3-ребер и 9 граней ^[25]
• 
  ₄ {4} ₂ {3} ₂ ,или, с 64 вершинами, 48 ребрами и 12 гранями
• 
  ₅ {4} ₂ {3} ₂ ,или, со 125 вершинами, 75 ребрами и 15 гранями
• 
  ₆ {4} ₂ {3} ₂ ,или, с 216 вершинами, 108 ребрами и 18 гранями
• 
  ₇ {4} ₂ {3} ₂ ,или, с 343 вершинами, 147 ребрами и 21 гранью
• 
  ₈ {4} ₂ {3} ₂ ,или, с 512 вершинами, 192 ребрами и 24 гранями
• 
  ₉ {4} ₂ {3} ₂ ,или, с 729 вершинами, 243 ребрами и 27 гранями
• 
  ₁₀ {4} ₂ {3} ₂ ,или, с 1000 вершинами, 300 ребрами и 30 гранями

Перечисление правильных комплексных 4-мерных многогранников

Коксетер перечислил этот список незвездных правильных комплексных 4-мерных многогранников в , включая 6 выпуклых правильных 4-мерных многогранников в . ^[23] ${\displaystyle \mathbb {C} ^{4}}$ ${\displaystyle \mathbb {R} ^{4}}$

Визуализации правильных комплексных 4-мерных многогранников

• 
  Реальные {3,3,3} ,, имел 5 вершин, 10 ребер, 10 {3} граней и 5 {3,3} ячеек
• 
  Реальные {3,4,3} ,, имел 24 вершины, 96 ребер, 96 {3} граней и 24 {3,4} ячейки
• 
  Реальные {5,3,3} ,, имел 600 вершин, 1200 ребер, 720 {5} граней и 120 {5,3} ячеек
• 
  Реальные {3,3,5} ,, имел 120 вершин, 720 ребер, 1200 {3} граней и 600 {3,3} ячеек
• 
  Виттинг-политоп ,, имеет 240 вершин, 2160 3-ребер, 2160 3{3}3 граней и 240 3{3}3{3}3 ячеек

Обобщенные 4-ортоплексы

Обобщенные 4-ортоплексы имеют регулярную конструкцию, каки квазирегулярная форма как. Все элементы являются симплексами .

• 
  Реальные {3,3,4} ,или, с 8 вершинами, 24 ребрами, 32 гранями и 16 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₃ ,или, с 12 вершинами, 54 ребрами, 108 гранями и 81 ячейкой
• 
  ₂ {3} ₂ {3} ₂ {4} ₄ ,или, с 16 вершинами, 96 ребрами, 256 гранями и 256 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₅ ,или, с 20 вершинами, 150 ребрами, 500 гранями и 625 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₆ ,или, с 24 вершинами, 216 ребрами, 864 гранями и 1296 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₇ ,или, с 28 вершинами, 294 ребрами, 1372 гранями и 2401 ячейкой
• 
  ₂ {3} ₂ {3} ₂ {4} ₈ ,или, с 32 вершинами, 384 ребрами, 2048 гранями и 4096 ячейками
• 
  ₂ {3} ₂ {3} ₂ {4} ₉ ,или, с 36 вершинами, 486 ребрами, 2916 гранями и 6561 ячейкой
• 
  ₂ {3} ₂ {3} ₂ {4} ₁₀ ,или, с 40 вершинами, 600 ребрами, 4000 гранями и 10000 ячеек

Обобщенные 4-кубы

Обобщенные тессеракты имеют правильную конструкцию:и призматическая конструкция как, произведение четырех p -угольных 1-многогранников. Элементы — обобщенные кубы меньшей размерности.

• 
  Реальные {4,3,3} ,или, с 16 вершинами, 32 ребрами, 24 гранями и 8 ячейками
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ ,или, с 81 вершиной, 108 ребрами, 54 гранями и 12 ячейками
• 
  ₄ {4} ₂ {3} ₂ {3} ₂ ,или, с 256 вершинами, 96 ребрами, 96 гранями и 16 ячейками
• 
  ₅ {4} ₂ {3} ₂ {3} ₂ ,или, с 625 вершинами, 500 ребрами, 150 гранями и 20 ячейками
• 
  ₆ {4} ₂ {3} ₂ {3} ₂ ,или, с 1296 вершинами, 864 ребрами, 216 гранями и 24 ячейками
• 
  ₇ {4} ₂ {3} ₂ {3} ₂ ,или, с 2401 вершиной, 1372 ребрами, 294 гранями и 28 ячейками
• 
  ₈ {4} ₂ {3} ₂ {3} ₂ ,или, с 4096 вершинами, 2048 ребрами, 384 гранями и 32 ячейками
• 
  ₉ {4} ₂ {3} ₂ {3} ₂ ,или, с 6561 вершиной, 2916 ребрами, 486 гранями и 36 ячейками
• 
  ₁₀ {4} ₂ {3} ₂ {3} ₂ ,или, с 10000 вершин, 4000 ребер, 600 граней и 40 ячеек

Перечисление правильных комплексных 5-мерных многогранников

Правильные комплексные 5-мерные многогранники в или выше существуют в трех семействах: действительные симплексы и обобщенные гиперкубы , а также ортоплексы . ${\displaystyle \mathbb {C} ^{5}}$

Визуализации правильных комплексных 5-мерных многогранников

Обобщенные 5-ортоплексы

Обобщенные 5-ортоплексы имеют регулярную конструкцию, каки квазирегулярная форма как. Все элементы являются симплексами .

• 
  Реальные {3,3,3,4} ,, с 10 вершинами, 40 ребрами, 80 гранями, 80 ячейками и 32 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₃ ,, с 15 вершинами, 90 ребрами, 270 гранями, 405 ячейками и 243 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₄ ,, с 20 вершинами, 160 ребрами, 640 гранями, 1280 ячейками и 1024 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₅ ,, с 25 вершинами, 250 ребрами, 1250 гранями, 3125 ячейками и 3125 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₆ ,, с 30 вершинами, 360 ребрами, 2160 гранями, 6480 ячейками, 7776 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₇ ,, с 35 вершинами, 490 ребрами, 3430 гранями, 12005 ячейками, 16807 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₈ ,, с 40 вершинами, 640 ребрами, 5120 гранями, 20480 ячейками, 32768 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₉ ,, с 45 вершинами, 810 ребрами, 7290 гранями, 32805 ячейками, 59049 4-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₁₀ ,, с 50 вершинами, 1000 рёбер, 10000 граней, 50000 ячеек, 100000 4-граней

Обобщенные 5-кубы

Обобщенные 5-кубы имеют правильную конструкциюи призматическая конструкция как, произведение пяти p -угольных 1-многогранников. Элементы — обобщенные кубы меньшей размерности.

• 
  Реальные {4,3,3,3} ,, с 32 вершинами, 80 ребрами, 80 гранями, 40 ячейками и 10 4-гранями
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 243 вершинами, 405 ребрами, 270 гранями, 90 ячейками и 15 4-гранями
• 
  ₄ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 1024 вершинами, 1280 ребрами, 640 гранями, 160 ячейками и 20 4-гранями
• 
  ₅ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 3125 вершинами, 3125 ребрами, 1250 гранями, 250 ячейками и 25 4-гранями
• 
  ₆ {4} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 7776 вершинами, 6480 ребрами, 2160 гранями, 360 ячейками и 30 4-гранями

Перечисление правильных комплексных 6-мерных многогранников

Визуализации правильных комплексных 6-мерных многогранников

Обобщенные 6-ортоплексы

Обобщенные 6-ортоплексы имеют регулярную конструкцию, каки квазирегулярная форма как. Все элементы являются симплексами .

• 
  Реальные {3,3,3,3,4} ,, с 12 вершинами, 60 ребрами, 160 гранями, 240 ячейками, 192 4-гранями и 64 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₃ ,, с 18 вершинами, 135 ребрами, 540 гранями, 1215 ячейками, 1458 4-гранями и 729 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₄ ,, с 24 вершинами, 240 ребрами, 1280 гранями, 3840 ячейками, 6144 4-гранями и 4096 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₅ ,, с 30 вершинами, 375 ребрами, 2500 гранями, 9375 ячейками, 18750 4-гранями и 15625 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₆ ,, с 36 вершинами, 540 ребрами, 4320 гранями, 19440 ячейками, 46656 4-гранями и 46656 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₇ ,, с 42 вершинами, 735 ребрами, 6860 гранями, 36015 ячейками, 100842 4-гранями, 117649 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₈ ,, с 48 вершинами, 960 ребрами, 10240 гранями, 61440 ячейками, 196608 4-гранями, 262144 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₉ ,, с 54 вершинами, 1215 ребрами, 14580 гранями, 98415 ячейками, 354294 4-гранями, 531441 5-гранями
• 
  ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ {4} ₁₀ ,, с 60 вершинами, 1500 ребрами, 20000 гранями, 150000 ячейками, 600000 4-гранями, 1000000 5-гранями

Обобщенные 6-кубы

Обобщенные 6-кубы имеют правильную конструкциюи призматическая конструкция как, произведение шести p -угольных 1-многогранников. Элементы — обобщенные кубы меньшей размерности.

• 
  Реальные {3,3,3,3,3,4} ,, с 64 вершинами, 192 ребрами, 240 гранями, 160 ячейками, 60 4-гранями и 12 5-гранями
• 
  ₃ {4} ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 729 вершинами, 1458 ребрами, 1215 гранями, 540 ячейками, 135 4-гранями и 18 5-гранями
• 
  ₄ {4} ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 4096 вершинами, 6144 ребрами, 3840 гранями, 1280 ячейками, 240 4-гранями и 24 5-гранями
• 
  ₅ {4} ₂ {3} ₂ {3} ₂ {3} ₂ {3} ₂ ,, с 15625 вершинами, 18750 ребрами, 9375 гранями, 2500 ячейками, 375 4-гранями и 30 5-гранями

Перечисление регулярных комплексных апейротопов

Коксетер перечислил этот список незвездных регулярных сложных апейротопов или сот. ^[28]

Для каждого измерения существует 12 апейротопов, обозначаемых как δ^{п , р}
_n+1существует в любых измерениях , или если p = q = 2. Коксетер называет эти обобщенные кубические соты для n > 2. ^[29] ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Каждый из них имеет пропорциональное количество элементов, определяемое как:

k-faces = , где и n ! обозначает факториал числа n . ${\displaystyle {n \choose k}p^{n-k}r^{k}}$ ${\displaystyle {n \choose m}={\frac {n!}{m!\,(n-m)!}}}$

Правильные комплексные 1-многогранники

Единственный правильный комплексный 1-многогранник — это _∞ {}, или. Его реальное представление — апейрогон , {∞}, или.

Правильные сложные апейрогоны

Некоторые подгруппы апейрогональных групп Шепарда

11 сложных апейрогонов _p { q } _r с внутренними частями ребер, окрашенными в светло-голубой цвет, и ребрами вокруг одной вершины, окрашенными индивидуально. Вершины показаны как маленькие черные квадраты. Ребра видны как p -сторонние правильные многоугольники, а вершинные фигуры являются r -угольными.

Квазиправильный апейрогонпредставляет собой смесь двух правильных апейрогонови, здесь с синими и розовыми краями.имеет только один цвет ребер, поскольку q нечетное, что делает его двойным покрытием.

Комплексные апейрогоны ранга 2 имеют симметрию _p [ q ] _r , где 1/ p + 2/ q + 1/ r = 1. Коксетер выражает их как δ^{п , р}
₂где q ограничено, чтобы удовлетворить q = 2/(1 – ( p + r )/ pr ) . ^[30]

Есть 8 решений:

Имеются два исключенных решения с нечетным q и неравными p и r : ₁₀ [5] ₂ и ₁₂ [3] ₄ , или и .

Правильный комплексный апейрогон _p { q } _r имеет p -рёбер и r -угольные вершинные фигуры. Двойственный апейрогон для _p { q } _r — это _r { q } _p . Апейрогон вида _p { q } _p является самодвойственным. Группы вида _p [2 q ] ₂ имеют половинную симметрию _p [ q ] _p , поэтому правильный апейрогонто же самое, что и квазирегулярный. ^[31]

Апейрогоны могут быть представлены на плоскости Аргана с четырьмя различными расположениями вершин. Апейрогоны вида ₂ { q } _r имеют расположение вершин как { q /2, p }. Вид _p { q } ₂ имеет расположение вершин как r{ p , q /2}. Апейрогоны вида _p {4} _r имеют расположение вершин { p , r }.

Включая аффинные узлы и , есть еще 3 бесконечных решения: _∞ [2] _∞ , _∞ [4] ₂ , _∞ [3] ₃ и ${\displaystyle \mathbb {C} ^{2}}$,, и. Первая является подгруппой индекса 2 второй. Вершины этих апейрогонов существуют в . ${\displaystyle \mathbb {C} ^{1}}$

Правильные комплексные апейроэдры

Существует 22 правильных комплексных апейроэдра вида _p { a } _q { b } _r . 8 из них самодвойственны ( p = r и a = b ), а 14 существуют как двойственные пары многогранников. Три из них полностью действительны ( p = q = r =2).

Коксетер символизирует 12 из них как δ^{п , р}
₃или _p {4} ₂ {4} _r — регулярная форма произведения апейротопов δ^{п , р}
₂× δ^{п , р}
₂или _p { q } _r × _p { q } _r , где q определяется из p и r .

то же самое, что и, а также, для p , r = 2,3,4,6. Также=. ^[33]

Регулярные комплексные 3-апейротопы

В 16 правильных комплексных апейротопов . Коксетер выражает 12 из них через δ ${\displaystyle \mathbb {C} ^{3}}$^{п , р}
₃где q ограничено, чтобы удовлетворить q = 2/(1 – ( p + r )/ pr ) . Их также можно разложить как произведение апейротопов:=. Первый случай — кубические соты . ${\displaystyle \mathbb {R} ^{3}}$

Regular complex 4-apeirotopes

There are 15 regular complex apeirotopes in ${\displaystyle \mathbb {C} ^{4}}$. Coxeter expresses 12 of them by δ^p,r
₄ where q is constrained to satisfy q = 2/(1 – (p + r)/pr). These can also be decomposed as product apeirotopes: = . The first case is the ${\displaystyle \mathbb {R} ^{4}}$ tesseractic honeycomb. The 16-cell honeycomb and 24-cell honeycomb are real solutions. The last solution is generated has Witting polytope elements.

Regular complex 5-apeirotopes and higher

There are only 12 regular complex apeirotopes in ${\displaystyle \mathbb {C} ^{5}}$ or higher,^[35] expressed δ^p,r
_n where q is constrained to satisfy q = 2/(1 – (p + r)/pr). These can also be decomposed a product of n apeirogons: ... = ... . The first case is the real ${\displaystyle \mathbb {R} ^{n}}$ hypercube honeycomb.

van Oss polygon

A red square van Oss polygon in the plane of an edge and center of a regular octahedron.

A van Oss polygon is a regular polygon in the plane (real plane ${\displaystyle \mathbb {R} ^{2}}$, or unitary plane ${\displaystyle \mathbb {C} ^{2}}$) in which both an edge and the centroid of a regular polytope lie, and formed of elements of the polytope. Not all regular polytopes have Van Oss polygons.

For example, the van Oss polygons of a real octahedron are the three squares whose planes pass through its center. In contrast a cube does not have a van Oss polygon because the edge-to-center plane cuts diagonally across two square faces and the two edges of the cube which lie in the plane do not form a polygon.

Infinite honeycombs also have van Oss apeirogons. For example, the real square tiling and triangular tiling have apeirogons {∞} van Oss apeirogons.^[36]

If it exists, the van Oss polygon of regular complex polytope of the form _p{q}_r{s}_t... has p-edges.

Non-regular complex polytopes

Product complex polytopes

Some complex polytopes can be represented as Cartesian products. These product polytopes are not strictly regular since they'll have more than one facet type, but some can represent lower symmetry of regular forms if all the orthogonal polytopes are identical. For example, the product _p{}×_p{} or of two 1-dimensional polytopes is the same as the regular _p{4}₂ or . More general products, like _p{}×_q{} have real representations as the 4-dimensional p-q duoprisms. The dual of a product polytope can be written as a sum _p{}+_q{} and have real representations as the 4-dimensional p-q duopyramid. The _p{}+_p{} can have its symmetry doubled as a regular complex polytope ₂{4}_p or .

Similarly, a ${\displaystyle \mathbb {C} ^{3}}$ complex polyhedron can be constructed as a triple product: _p{}×_p{}×_p{} or is the same as the regular generalized cube, _p{4}₂{3}₂ or , as well as product _p{4}₂×_p{} or .^[37]

Quasiregular polygons

A quasiregular polygon is a truncation of a regular polygon. A quasiregular polygon contains alternate edges of the regular polygons and . The quasiregular polygon has p vertices on the p-edges of the regular form.

Quasiregular apeirogons

There are 7 quasiregular complex apeirogons which alternate edges of a regular apeirogon and its regular dual. The vertex arrangements of these apeirogon have real representations with the regular and uniform tilings of the Euclidean plane. The last column for the 6{3}6 apeirogon is not only self-dual, but the dual coincides with itself with overlapping hexagonal edges, thus their quasiregular form also has overlapping hexagonal edges, so it can't be drawn with two alternating colors like the others. The symmetry of the self-dual families can be doubled, so creating an identical geometry as the regular forms: =

Quasiregular polyhedra

Example truncation of 3-generalized octahedron, ₂{3}₂{4}₃, , to its rectified limit, showing outlined-green triangles faces at the start, and blue ₂{4}₃, , vertex figures expanding as new faces.

Like real polytopes, a complex quasiregular polyhedron can be constructed as a rectification (a complete truncation) of a regular polyhedron. Vertices are created mid-edge of the regular polyhedron and faces of the regular polyhedron and its dual are positioned alternating across common edges.

For example, a p-generalized cube, , has p³ vertices, 3p² edges, and 3p p-generalized square faces, while the p-generalized octahedron, , has 3p vertices, 3p² edges and p³ triangular faces. The middle quasiregular form p-generalized cuboctahedron, , has 3p² vertices, 3p³ edges, and 3p+p³ faces.

Also the rectification of the Hessian polyhedron , is , a quasiregular form sharing the geometry of the regular complex polyhedron .

Other complex polytopes with unitary reflections of period two

Other nonregular complex polytopes can be constructed within unitary reflection groups that don't make linear Coxeter graphs. In Coxeter diagrams with loops Coxeter marks a special period interior, like or symbol (1₁ 1 1)³, and group [1 1 1]³.^[38][39] These complex polytopes have not been systematically explored beyond a few cases.

The group is defined by 3 unitary reflections, R₁, R₂, R₃, all order 2: R₁² = R₁² = R₃² = (R₁R₂)³ = (R₂R₃)³ = (R₃R₁)³ = (R₁R₂R₃R₁)^p = 1. The period p can be seen as a double rotation in real ${\displaystyle \mathbb {R} ^{4}}$.

As with all Wythoff constructions, polytopes generated by reflections, the number of vertices of a single-ringed Coxeter diagram polytope is equal to the order of the group divided by the order of the subgroup where the ringed node is removed. For example, a real cube has Coxeter diagram , with octahedral symmetry order 48, and subgroup dihedral symmetry order 6, so the number of vertices of a cube is 48/6=8. Facets are constructed by removing one node furthest from the ringed node, for example for the cube. Vertex figures are generated by removing a ringed node and ringing one or more connected nodes, and for the cube.

Coxeter represents these groups by the following symbols. Some groups have the same order, but a different structure, defining the same vertex arrangement in complex polytopes, but different edges and higher elements, like and with p≠3.^[40]

Coxeter calls some of these complex polyhedra almost regular because they have regular facets and vertex figures. The first is a lower symmetry form of the generalized cross-polytope in ${\displaystyle \mathbb {C} ^{3}}$. The second is a fractional generalized cube, reducing p-edges into single vertices leaving ordinary 2-edges. Three of them are related to the finite regular skew polyhedron in ${\displaystyle \mathbb {R} ^{4}}$.

Coxeter defines other groups with anti-unitary constructions, for example these three. The first was discovered and drawn by Peter McMullen in 1966.^[42]

Visualizations

• 
  (1 1 1₁⁴)⁴, has 42 vertices, 168 edges and 112 triangular faces, seen in this 14-gonal projection.
• 
  (1⁴ 1⁴ 1₁)⁽³⁾, has 56 vertices, 168 edges and 84 square faces, seen in this 14-gonal projection.
• 
  (1 1 2₂)⁴, has 80 vertices, 640 edges, 1280 triangular faces and 640 tetrahedral cells, seen in this 20-gonal projection.^[43]

See also

• Quaternionic polytope

Notes

1. Peter Orlik, Victor Reiner, Anne V. Shepler. The sign representation for Shephard groups. Mathematische Annalen. March 2002, Volume 322, Issue 3, pp 477–492. DOI:10.1007/s002080200001 [1]
2. Coxeter, Regular Complex Polytopes, p. 115
3. Coxeter, Regular Complex Polytopes, 11.3 Petrie Polygon, a simple h-gon formed by the orbit of the flag (O₀,O₀O₁) for the product of the two generating reflections of any nonstarry regular complex polygon, p₁{q}p₂.
4. Complex Regular Polytopes,11.1 Regular complex polygons p.103
5. Shephard, 1952; "It is from considerations such as these that we derive the notion of the interior of a polytope, and it will be seen that in unitary space where the numbers cannot be so ordered such a concept of interior is impossible. [Para break] Hence ... we have to consider unitary polytopes as configurations."
6. Coxeter, Regular Complex polytopes, p. 96
7. Coxeter, Regular Complex Polytopes, p. xiv
8. Coxeter, Complex Regular Polytopes, p. 177, Table III
9. Lehrer & Taylor 2009, p. 87
10. Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. pp. 178–179
11. Complex Polytopes, 8.9 The Two-Dimensional Case, p. 88
12. Regular Complex Polytopes, Coxeter, pp. 177-179
13. Coxeter, Regular Complex Polytopes, p. 108
14. Coxeter, Regular Complex Polytopes, p. 109
15. Coxeter, Regular Complex Polytopes, p. 111
16. Coxeter, Regular Complex Polytopes, p. 30 diagram and p. 47 indices for 8 3-edges
17. Coxeter, Regular Complex Polytopes, p. 110
18. Coxeter, Regular Complex Polytopes, p. 48
19. Coxeter, Regular Complex Polytopes, p. 49
20. Coxeter, Regular Complex Polytopes, pp. 116–140.
21. Coxeter, Regular Complex Polytopes, pp. 118–119.
22. Complex Regular Polytopes, p.29
23. Coxeter, Regular Complex Polytopes, Table V. The nonstarry regular polyhedra and 4-polytopes. p. 180.
24. Coxeter, Kaleidoscopes — Selected Writings of H.S.M. Coxeter, Paper 25 Surprising relationships among unitary reflection groups, p. 431.
25. Coxeter, Regular Complex Polytopes, p. 131
26. Coxeter, Regular Complex Polytopes, p. 126
27. Coxeter, Regular Complex Polytopes, p. 125
28. Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 180.
29. Complex regular polytope, p.174
30. Coxeter, Regular Complex Polytopes, Table VI. The regular honeycombs. p. 111, 136.
31. Coxeter, Regular Complex Polytopes, Table IV. The regular polygons. pp. 178–179
32. Coxeter, Regular Complex Polytopes, 11.6 Apeirogons, pp. 111-112
33. Coxeter, Complex Regular Polytopes, p.140
34. Coxeter, Regular Complex Polytopes, pp. 139-140
35. Complex Regular Polytopes, p.146
36. Complex Regular Polytopes, p.141
37. Coxeter, Regular Complex Polytopes, pp. 118–119, 138.
38. Coxeter, Regular Complex Polytopes, Chapter 14, Almost regular polytopes, pp. 156–174.
39. Коксетер, Группы, порожденные унитарными отражениями периода два , 1956
40. Коксетер , Конечные группы, порожденные унитарными отражениями , 1966, 4. Графическая нотация , Таблица n -мерных групп, порожденных n унитарными отражениями. С. 422-423
41. Коксетер, Группы, порожденные унитарными отражениями периода два (1956), Таблица III: Некоторые сложные многогранники, стр.413
42. Коксетер, Комплексные правильные многогранники, (1991), 14.6 Два многогранника МакМаллена с 84 квадратными гранями, стр. 166-171
43. Коксетер, Комплексные правильные многогранники, стр. 172-173

Ссылки

• Коксетер, Х. С. М. и Мозер, У. О. Дж.; Генераторы и соотношения для дискретных групп (1965), особенно стр. 67–80.
• Коксетер, HSM (1991), Правильные комплексные многогранники , Cambridge University Press, ISBN 0-521-39490-2
• Коксетер, Х. С. М. и Шепард, Г. К.; Портреты семейства сложных многогранников, Leonardo Vol 25, No 3/4, (1992), стр. 239–244,
• Шепард, GC; Правильные комплексные многогранники , Proc. London math. Soc. Series 3, Vol 2, (1952), стр. 82–97.
• GC Shephard , JA Todd, Конечные унитарные группы отражений , Канадский журнал математики. 6(1954), 274-304, doi :10.4153/CJM-1954-028-3
• Густав И. Лерер и Дональд Э. Тейлор, «Группы единой рефлексии» , Cambridge University Press, 2009

Дальнейшее чтение

• Ф. Артур Шерк, Питер МакМаллен, Энтони К. Томпсон и Азия Ивич Вайс, редакторы: Kaleidoscopes — Selected Writings of HSM Coxeter. , Статья 25, Конечные группы, порожденные унитарными отражениями , стр. 415-425, John Wiley, 1995, ISBN 0-471-01003-0 
• МакМаллен, Питер ; Шульте, Эгон (декабрь 2002 г.), Абстрактные правильные многогранники (1-е изд.), Cambridge University Press , ISBN 0-521-81496-0Глава 9 Унитарные группы и эрмитовы формы , стр. 289–298