Вынужденное излучение

Высвобождение фотона, вызванное другим

Лазерный свет — это разновидность вынужденного излучения.

Вынужденное излучение — это процесс, при котором входящий фотон определенной частоты может взаимодействовать с возбужденным атомным электроном (или другим возбужденным молекулярным состоянием), заставляя его опуститься на более низкий энергетический уровень. Освобожденная энергия передается электромагнитному полю, создавая новый фотон с частотой , поляризацией и направлением движения, которые идентичны фотонам падающей волны. Это отличается от спонтанного излучения , которое происходит с характерной скоростью для каждого из атомов/осцилляторов в верхнем энергетическом состоянии независимо от внешнего электромагнитного поля.

По данным Американского физического общества , первым человеком, который правильно предсказал явление вынужденного излучения, был Альберт Эйнштейн в серии статей, начавшихся в 1916 году, кульминацией которых стало то, что сейчас называется коэффициентом Эйнштейна B. Работа Эйнштейна стала теоретической основой мазера и лазера . [ ^{1] [2] [3] [4]} Процесс по форме идентичен атомному поглощению , в котором энергия поглощенного фотона вызывает идентичный, но противоположный атомный переход: с нижнего уровня на более высокий энергетический уровень. В обычных средах при тепловом равновесии поглощение превышает вынужденное излучение, поскольку в состояниях с более низкой энергией больше электронов, чем в состояниях с более высокой энергией. Однако при наличии инверсии населенности скорость вынужденного излучения превышает скорость поглощения, и может быть достигнуто чистое оптическое усиление . Такая усиливающая среда , наряду с оптическим резонатором, является сердцем лазера или мазера. Не имея механизма обратной связи, лазерные усилители и суперлюминесцентные источники также функционируют на основе вынужденного излучения.

Обзор

Электроны и их взаимодействие с электромагнитными полями важны для нашего понимания химии и физики . В классическом представлении энергия электрона, вращающегося вокруг атомного ядра, больше для орбит, удаленных от ядра атома . Однако квантово-механические эффекты заставляют электроны занимать дискретные положения на орбиталях . Таким образом, электроны находятся на определенных энергетических уровнях атома, два из которых показаны ниже:

Когда электрон поглощает энергию либо от света (фотонов), либо от тепла ( фононов ), он получает этот падающий квант энергии. Но переходы разрешены только между дискретными уровнями энергии, такими как два, показанные выше. Это приводит к линиям испускания и линиям поглощения .

Когда электрон возбуждается с более низкого на более высокий энергетический уровень, маловероятно, что он останется таким навсегда. Электрон в возбужденном состоянии может распасться на более низкое энергетическое состояние, которое не занято, в соответствии с определенной постоянной времени, характеризующей этот переход. Когда такой электрон распадается без внешнего воздействия, испуская фотон, это называется « спонтанным излучением ». Фаза и направление, связанные с испускаемым фотоном, являются случайными. Материал со многими атомами в таком возбужденном состоянии может, таким образом, привести к излучению , которое имеет узкий спектр (сосредоточенный вокруг одной длины волны света), но отдельные фотоны не будут иметь общего фазового соотношения и также будут испускаться в случайных направлениях. Это механизм флуоресценции и теплового излучения .

Внешнее электромагнитное поле на частоте, связанной с переходом, может влиять на квантово-механическое состояние атома, не поглощаясь. Когда электрон в атоме совершает переход между двумя стационарными состояниями (ни одно из которых не показывает дипольного поля), он переходит в переходное состояние, которое имеет дипольное поле и действует как небольшой электрический диполь , и этот диполь колеблется с характерной частотой. В ответ на внешнее электрическое поле на этой частоте вероятность перехода электрона в это переходное состояние значительно увеличивается. Таким образом, скорость переходов между двумя стационарными состояниями увеличивается по сравнению со скоростью спонтанного излучения. Переход из состояния с более высокой энергией в состояние с более низкой энергией производит дополнительный фотон с той же фазой и направлением, что и падающий фотон; это процесс вынужденного излучения.

История

Вынужденное излучение было теоретическим открытием Альберта Эйнштейна ^{[5] [6]} в рамках старой квантовой теории , в которой излучение описывается в терминах фотонов, которые являются квантами электромагнитного поля. Вынужденное излучение может также происходить в классических моделях, без ссылки на фотоны или квантовую механику. ^[7] (См. также Laser § History .) По словам профессора физики и директора Центра ультрахолодных атомов Массачусетского технологического института и Гарварда Дэниела Клеппнера , теория излучения Эйнштейна опередила свое время и предвосхищает современную теорию квантовой электродинамики и квантовой оптики на несколько десятилетий. ^[8]

Математическая модель

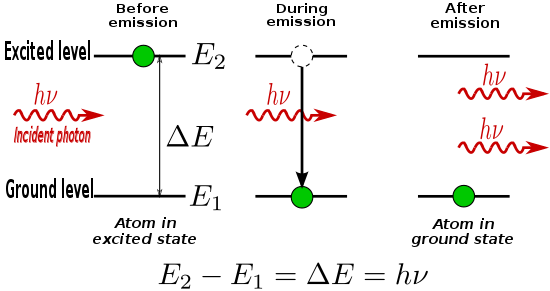
Вынужденное излучение можно смоделировать математически, рассмотрев атом, который может находиться в одном из двух электронных энергетических состояний: состоянии более низкого уровня (возможно, основном состоянии) (1) и возбужденном состоянии (2), с энергиями E ₁ и E ₂ соответственно.

Если атом находится в возбужденном состоянии, он может распасться на более низкое состояние в процессе спонтанного излучения , высвобождая разницу в энергиях между двумя состояниями в виде фотона. Фотон будет иметь частоту ν ₀ и энергию hν ₀ , определяемую как: где h — постоянная Планка . $${\displaystyle E_{2}-E_{1}=h\,\nu _{0}}$$

В качестве альтернативы, если возбужденный атом возмущен электрическим полем частоты ν ₀ , он может испустить дополнительный фотон той же частоты и в фазе, тем самым увеличивая внешнее поле, оставляя атом в состоянии с более низкой энергией. Этот процесс известен как вынужденное излучение.

В группе таких атомов, если число атомов в возбужденном состоянии дается как N ₂ , скорость, с которой происходит вынужденное излучение, дается как где константа пропорциональности B ₂₁ известна как коэффициент Эйнштейна B для этого конкретного перехода, а ρ ( ν ) является плотностью излучения падающего поля на частоте ν . Таким образом, скорость излучения пропорциональна числу атомов в возбужденном состоянии N ₂ и плотности падающих фотонов. $${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=-B_{21}\,\rho (\nu )\,N_{2}}$$

В то же время будет происходить процесс атомной абсорбции, который удаляет энергию из поля, одновременно поднимая электроны из нижнего состояния в верхнее. Его скорость определяется по существу идентичным уравнением, $${\displaystyle {\frac {\partial N_{2}}{\partial t}}=-{\frac {\partial N_{1}}{\partial t}}=B_{12}\,\rho (\nu )\,N_{1}.}$$

Скорость поглощения, таким образом, пропорциональна числу атомов в нижнем состоянии, N ₁ . Коэффициенты B можно рассчитать с помощью дипольного приближения и зависящей от времени теории возмущений в квантовой механике как: ^{[9] [10]} где B соответствует распределению энергии в терминах частоты ν . Коэффициент B может меняться в зависимости от выбора используемой функции распределения энергии, однако произведение функции распределения энергии и соответствующего ей коэффициента B остается прежним. $${\displaystyle B_{ab}={\frac {e^{2}}{6\epsilon _{0}\hbar ^{2}}}|\langle a|{\vec {r}}|b\rangle |^{2}}$$

Эйнштейн показал на основе формы закона Планка ^{[ необходима ссылка ]} , что коэффициент для этого перехода должен быть идентичен коэффициенту для вынужденного излучения: $${\displaystyle B_{12}=B_{21}.}$$

Таким образом, поглощение и вынужденное испускание являются обратными процессами, протекающими с несколько разными скоростями. Другой способ рассмотрения этого - рассмотреть чистое вынужденное испускание или поглощение, рассматривая его как единый процесс. Чистая скорость переходов из E ₂ в E ₁ из-за этого объединенного процесса может быть найдена путем сложения их соответствующих скоростей, приведенных выше: $${\displaystyle {\frac {\partial N_{1}^{\text{net}}}{\partial t}}=-{\frac {\partial N_{2}^{\text{net}}}{\partial t}}=B_{21}\,\rho (\nu )\,(N_{2}-N_{1})=B_{21}\,\rho (\nu )\,\Delta N.}$$

Таким образом, чистая мощность выделяется в электрическое поле, равное энергии фотона hν , ​​умноженной на эту чистую скорость перехода. Для того чтобы это было положительным числом, указывающим на чистое стимулированное излучение, в возбужденном состоянии должно быть больше атомов, чем на нижнем уровне: . В противном случае происходит чистое поглощение, и мощность волны уменьшается при прохождении через среду. Особое условие известно как инверсия населенности , довольно необычное условие, которое должно быть достигнуто в среде усиления лазера. ${\displaystyle \Delta N>0}$ ${\displaystyle N_{2}>N_{1}}$

Отличительной особенностью стимулированного излучения по сравнению с обычными источниками света (которые зависят от спонтанного излучения) является то, что испускаемые фотоны имеют ту же частоту, фазу, поляризацию и направление распространения, что и падающие фотоны. Таким образом, участвующие фотоны взаимно когерентны . Когда присутствует инверсия населенности ( ), следовательно, будет иметь место оптическое усиление падающего излучения. ${\displaystyle \Delta N>0}$

Хотя энергия, генерируемая стимулированным излучением, всегда находится на точной частоте поля, которое его стимулировало, приведенное выше уравнение скорости относится только к возбуждению на конкретной оптической частоте, соответствующей энергии перехода. На частотах, смещенных от силы стимулированного (или спонтанного) излучения, будет уменьшаться в соответствии с так называемой формой линии . Рассматривая только однородное уширение, влияющее на атомный или молекулярный резонанс, функция формы спектральной линии описывается как распределение Лоренца , где — полная ширина на половине максимума или ширина полосы пропускания FWHM. ${\displaystyle \nu _{0}}$ ${\displaystyle \nu _{0}}$ $${\displaystyle g'(\nu )={1 \over \pi }{(\Gamma /2) \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}}$$ ${\displaystyle \Gamma }$

Пиковое значение формы лоренцевской линии приходится на центр линии, . Функция формы линии может быть нормализована так, чтобы ее значение в было равно единице; в случае лоренцевской линии мы получаем ${\displaystyle \nu =\nu _{0}}$ ${\displaystyle \nu _{0}}$ $${\displaystyle g(\nu )={g'(\nu ) \over g'(\nu _{0})}={(\Gamma /2)^{2} \over (\nu -\nu _{0})^{2}+(\Gamma /2)^{2}}.}$$

Таким образом, вынужденное излучение на частотах, далеких от уменьшается этим фактором. На практике также может быть расширение формы линии из-за неоднородного расширения , в первую очередь из-за эффекта Доплера, возникающего из-за распределения скоростей в газе при определенной температуре. Это имеет гауссову форму и уменьшает пиковую силу функции формы линии. В практической задаче полная функция формы линии может быть вычислена посредством свертки отдельных задействованных функций формы линии. Следовательно, оптическое усиление будет добавлять мощность к падающему оптическому полю на частоте со скоростью, заданной как ${\displaystyle \nu _{0}}$ ${\displaystyle \nu }$ $${\displaystyle P=h\nu \,g(\nu )\,B_{21}\,\rho (\nu )\,\Delta N.}$$

Сечение вынужденного излучения

Сечение вынужденного излучения находится там, где $${\displaystyle \sigma _{21}(\nu )=A_{21}{\frac {\lambda ^{2}}{8\pi n^{2}}}g'(\nu )}$$

• A ₂₁ — коэффициент Эйнштейна А ,
• λ — длина волны в вакууме,
• n — показатель преломления среды (безразмерный), а
• g ′( ν ) — функция формы спектральной линии.

Оптическое усиление

Вынужденное излучение может обеспечить физический механизм для оптического усиления . Если внешний источник энергии стимулирует более 50% атомов в основном состоянии к переходу в возбужденное состояние, то создается то, что называется инверсией населенности . Когда свет соответствующей частоты проходит через инвертированную среду, фотоны либо поглощаются атомами, которые остаются в основном состоянии, либо фотоны стимулируют возбужденные атомы испускать дополнительные фотоны той же частоты, фазы и направления. Поскольку в возбужденном состоянии находится больше атомов, чем в основном состоянии, то происходит усиление входной интенсивности .

Инверсия населенности, выраженная в единицах атомов на кубический метр, составляет

${\displaystyle \Delta N_{21}=N_{2}-{g_{2} \over g_{1}}N_{1}}$

где g ₁ и g ₂ — вырождения уровней энергии 1 и 2 соответственно.

Уравнение усиления слабого сигнала

Интенсивность (в ваттах на квадратный метр) вынужденного излучения регулируется следующим дифференциальным уравнением:

${\displaystyle {dI \over dz}=\sigma _{21}(\nu )\cdot \Delta N_{21}\cdot I(z)}$

пока интенсивность I ( z ) достаточно мала, чтобы не оказывать существенного влияния на величину инверсии населенности. Группируя первые два фактора вместе, это уравнение упрощается как

${\displaystyle {dI \over dz}=\gamma _{0}(\nu )\cdot I(z)}$

где

${\displaystyle \gamma _{0}(\nu )=\sigma _{21}(\nu )\cdot \Delta N_{21}}$

- коэффициент усиления слабого сигнала (в радианах на метр). Мы можем решить дифференциальное уравнение, используя разделение переменных :

${\displaystyle {dI \over I(z)}=\gamma _{0}(\nu )\cdot dz}$

Интегрируя, находим:

${\displaystyle \ln \left({I(z) \over I_{in}}\right)=\gamma _{0}(\nu )\cdot z}$

или

${\displaystyle I(z)=I_{in}e^{\gamma _{0}(\nu )z}}$

где

${\displaystyle I_{in}=I(z=0)\,}$оптическая интенсивность входного сигнала (в ваттах на квадратный метр).

Интенсивность насыщения

Интенсивность насыщения I _S определяется как входная интенсивность, при которой усиление оптического усилителя падает ровно до половины усиления слабого сигнала. Мы можем вычислить интенсивность насыщения как

${\displaystyle I_{S}={h\nu \over \sigma (\nu )\cdot \tau _{S}}}$

где

${\displaystyle h}$- постоянная Планка , а

${\displaystyle \tau _{\text{S}}}$— постоянная времени насыщения, которая зависит от времени жизни спонтанного излучения различных переходов между уровнями энергии, связанными с усилением.

${\displaystyle \nu }$частота в Гц

Минимальное значение имеет место при резонансе, ^[11] , где поперечное сечение наибольшее. Это минимальное значение равно: ${\displaystyle I_{\text{S}}(\nu )}$ ${\displaystyle \sigma (\nu )}$

${\displaystyle I_{\text{sat}}={\frac {\pi }{3}}{hc \over \lambda ^{3}\tau _{S}}}$

Для простого двухуровневого атома с естественной шириной линии постоянная времени насыщения . ${\displaystyle \Gamma }$ ${\displaystyle \tau _{\text{S}}=\Gamma ^{-1}}$

Общее уравнение усиления

Общая форма уравнения усиления, которая применяется независимо от входной интенсивности, выводится из общего дифференциального уравнения для интенсивности I как функции положения z в среде усиления :

${\displaystyle {dI \over dz}={\gamma _{0}(\nu ) \over 1+{\bar {g}}(\nu ){I(z) \over I_{S}}}\cdot I(z)}$

где - интенсивность насыщения. Для решения сначала переставим уравнение, чтобы разделить переменные, интенсивность I и положение z : ${\displaystyle I_{S}}$

${\displaystyle {dI \over I(z)}\left[1+{\bar {g}}(\nu ){I(z) \over I_{S}}\right]=\gamma _{0}(\nu )\cdot dz}$

Интегрируя обе части, получаем

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I(z)-I_{in} \over I_{S}}=\gamma _{0}(\nu )\cdot z}$

или

${\displaystyle \ln \left({I(z) \over I_{in}}\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left({I(z) \over I_{in}}-1\right)=\gamma _{0}(\nu )\cdot z}$

Коэффициент усиления G усилителя определяется как оптическая интенсивность I в позиции z, деленная на входную интенсивность:

${\displaystyle G=G(z)={I(z) \over I_{in}}}$

Подставляя это определение в предыдущее уравнение, находим общее уравнение усиления :

${\displaystyle \ln \left(G\right)+{\bar {g}}(\nu ){I_{in} \over I_{S}}\left(G-1\right)=\gamma _{0}(\nu )\cdot z}$

Приближение малого сигнала

В частном случае, когда входной сигнал мал по сравнению с интенсивностью насыщения, другими словами,

${\displaystyle I_{in}\ll I_{S}\,}$

тогда общее уравнение усиления дает усиление малого сигнала как

${\displaystyle \ln(G)=\ln(G_{0})=\gamma _{0}(\nu )\cdot z}$

или

${\displaystyle G=G_{0}=e^{\gamma _{0}(\nu )z}}$

что идентично уравнению усиления слабого сигнала (см. выше).

Асимптотическое поведение большого сигнала

Для больших входных сигналов, где

${\displaystyle I_{in}\gg I_{S}\,}$

прирост приближается к единице

${\displaystyle G\rightarrow 1}$

и общее уравнение усиления приближается к линейной асимптоте :

${\displaystyle I(z)=I_{in}+{\gamma _{0}(\nu )\cdot z \over {\bar {g}}(\nu )}I_{S}}$

Смотрите также

• Поглощение
• Активная лазерная среда
• Лазер (включая раздел истории )
• Лазерная наука
• цикл Раби
• Спонтанное излучение
• STED-микроскопия
• Коэффициенты Эйнштейна

Ссылки

1. Треткофф, Эрни (август 2005 г.). «Этот месяц в истории физики: Эйнштейн предсказывает вынужденное излучение». Новости Американского физического общества . 14 (8) . Получено 1 июня 2022 г.
2. Штрауманн, Норберт (23 марта 2017 г.). «Эйнштейн в 1916 г.: «О квантовой теории излучения»". arXiv : 1703.08176 [физика.хист-ф].
3. Хехт, Джефф (15 августа 2021 г.). «Лазер». Encyclopedia Britannica . Получено 1 июня 2022 г.
4. Стоун, А. Дуглас (6 октября 2013 г.). Эйнштейн и квант: поиски доблестного шваба (первое издание). Princeton University Press. ISBN 978-0691139685. Получено 1 июня 2022 г. .
5. Эйнштейн, А (1916). «Излучение и поглощение излучения в квантовой теории». Verhandlungen der Deutschen Physikalischen Gesellschaft . 18 : 318–323. Бибкод : 1916DPhyG..18..318E.
6. Эйнштейн, А (1917). «Квантовая теория излучения». Physikalische Zeitschrift . 18 : 121–128. Бибкод : 1917PhyZ...18..121E.
7. Fain, B.; Milonni, PW (1987). "Классическое стимулированное излучение". Журнал оптического общества Америки B. 4 ( 1): 78. Bibcode : 1987JOSAB...4...78F. doi : 10.1364/JOSAB.4.000078.
8. Клеппнер, Дэниел (1 февраля 2005 г.). «Перечитывая Эйнштейна о радиации». Physics Today . 58 (2): 30–33. Bibcode : 2005PhT....58b..30K. doi : 10.1063/1.1897520 . Получено 1 июня 2022 г.
9. Хилборн, Роберт (2002). «Коэффициенты Эйнштейна, сечения, значения f, дипольные моменты и все такое» (PDF) .
10. Сегре, Карло. «Коэффициенты Эйнштейна — Основы квантовой теории II (PHYS 406)» (PDF) . стр. 32.
11. Фут, CJ (2005). Атомная физика. Oxford University Press. стр. 142. ISBN 978-0-19-850695-9.

• Салех, Бахаа Э.А. и Тейх, Малвин Карл (1991). Основы фотоники . Нью-Йорк: Джон Уайли и сыновья. ISBN 0-471-83965-5.
• Алан Корни (1977). Атомная и лазерная спектроскопия . Оксфорд: Oxford Uni. Press. ISBN 0-19-921145-0. ISBN  978-0-19-921145-6 .