Сабит ибн Курра (полное имя: Абу аль-Хасан ибн Захрун аль-Харрани аль-Саби , арабский : أبو الحسن ثابت بن قرة بن زهرون الحراني ابئ , латынь : Фебит/Фебит/Тебит [2] 826 или 836 — 19 февраля, 901), [3] был эрудитом, известным своими работами в области математики , медицины , астрономии и перевода . Он жил в Багдаде во второй половине IX века во времена Аббасидского халифата .
Сабит ибн Курра сделал важные открытия в алгебре , геометрии и астрономии . В астрономии Сабит считается одним из первых реформаторов системы Птолемея , а в механике он был основателем статики . [4] Сабит также много писал о медицине и создал философские трактаты. [5]
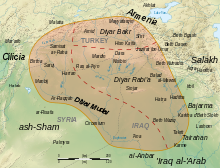
Сабит родился в Харране в Верхней Месопотамии , которая в то время была частью Дияр Мударского подразделения региона Аль-Джазира Аббасидского халифата . Сабит принадлежал к сабиям Харрана , эллинизированной семитской политеистической астральной религии , которая все еще существовала в Харране девятого века. [6]
В юности Сабит работал менялой на рынке в Харране, пока не встретил Мухаммада ибн Мусу, старейшего из трех математиков и астрономов, известных как Бану Муса . Сабит проявил такие исключительные лингвистические способности, что ибн Муса выбрал его для приезда в Багдад, чтобы он обучался математике, астрономии и философии под руководством Бану Муса. Здесь Сабит был представлен не только сообществу ученых, но и тем, кто имел значительную власть и влияние в Багдаде. [7] [8]
Сабит и его ученики жили в самом интеллектуально ярком и, вероятно, самом большом городе того времени, Багдаде . Сабит приехал в Багдад в первую очередь, чтобы работать на Бану Муса, став частью их круга и помогая им переводить греческие математические тексты. [9] Неизвестно, как Бану Муса и Сабит занимались математикой, астрономией, астрологией, магией, механикой , медициной и философией . Позже в его жизни покровителем Сабита был халиф Аббасидов аль-Мутадид (правил в 892–902 гг.), у которого он стал придворным астрономом. [9] Сабит стал личным другом и придворным халифа. Сабит умер в Багдаде в 901 году. Его сын, Синан ибн Сабит, и внук, Ибрагим ибн Синан, также внесли вклад в медицину и науку. [10] К концу своей жизни Сабит успел написать 150 работ по математике, астрономии и медицине. [11] Несмотря на всю проделанную Сабитом работу, большая часть его работ не сохранилась. Сохранилось менее дюжины его работ. [10]

Родным языком Табита был сирийский [12] , который был среднеарамейским диалектом из Эдессы , и он свободно говорил как на средневековом греческом , так и на арабском [13] . Он был автором множества договоров. Благодаря тому, что он был трехъязычным, Табит смог сыграть важную роль в греко-арабском переводческом движении [10] . Он также создал школу перевода в Багдаде [11] .
Сабит перевел с греческого на арабский труды Аполлония Пергского , Архимеда , Евклида и Птолемея . Он переработал перевод « Начал » Евклида Хунайна ибн Исхака . Он также переписал перевод «Альмагеста » Птолемея , сделанный Исхаком ибн Хунайном , и перевел «Географию» Птолемея . Перевод Сабита работы Архимеда, в которой дано построение правильного семиугольника, был обнаружен в 20 веке, оригинал был утерян. [ требуется ссылка ]
Считается, что Сабит был астрономом халифа аль-Мутадида . [14] Сабит смог использовать свои математические работы при изучении птолемеевской астрономии . [10] Средневековая астрономическая теория трепета равноденствий часто приписывается Сабиту. [ необходима цитата ] Но она уже была описана Теоном Александрийским в его комментариях к Handy Tables Птолемея . Согласно Копернику , Сабит определил продолжительность сидерического года как 365 дней, 6 часов, 9 минут и 12 секунд (погрешность в 2 секунды). Коперник основывал свое утверждение на латинском тексте, приписываемом Сабиту. Сабит опубликовал свои наблюдения за Солнцем . [ необходима цитата ] Что касается планетарных гипотез Птолемея , Сабит исследовал проблемы движения Солнца и Луны, а также теорию солнечных часов. [10] Рассматривая гипотезы Птолемея, Сабит ибн Курра обнаружил сидерический год , который при наблюдении за Землей и измерении ее на фоне неподвижных звезд будет иметь постоянное значение. [15]
Табит также был автором и написал De Anno Solis. Эта книга содержала и записывала факты об эволюции астрономии в девятом веке. [14] Табит упоминал в книге, что Птолемей и Гиппарх считали, что движение звезд согласуется с движением, обычно обнаруживаемым у планет. Табит считал, что эту идею можно расширить, включив в нее Солнце и Луну. [14] Имея это в виду, он также считал, что солнечный год следует рассчитывать, рассматривая возвращение Солнца к данной звезде. [14]
В математике Табит вывел уравнение для определения дружественных чисел . Его доказательство этого правила представлено в « Трактате о выводе дружественных чисел простым способом» . [16] Это было сделано во время написания работы по теории чисел , расширив их использование для описания соотношений между геометрическими величинами, шаг, который греки не сделали. Работа Табита по дружественным числам и теории чисел помогла ему вложить больше средств в геометрические отношения чисел, устанавливая его теорему о трансверсали (геометрии) . [11] [16]
Табит описал обобщенное доказательство теоремы Пифагора . [17] Он предоставил усиленное расширение [ требуется разъяснение ] доказательства Пифагора, которое включало знание пятого постулата Евклида . [18] Этот постулат гласит, что пересечение двух прямых отрезков объединяется, чтобы создать два внутренних угла, которые меньше 180 градусов. Метод редукции и композиции [ требуется разъяснение ], используемый Табитом, привел к объединению и расширению [ требуется разъяснение ] современных и древних знаний об этом знаменитом доказательстве. Табит считал, что геометрия связана с равенством и разностью величин линий и углов, [ требуется разъяснение ] , а также что идеи движения (и идеи, взятые из физики в более широком смысле) должны быть интегрированы в геометрию. [19] [ требуется разъяснение ]
Продолжение работы над геометрическими отношениями и полученный экспоненциальный ряд позволили Табиту вычислить несколько решений шахматных задач . Эта проблема была связана не столько с самой игрой, сколько с количеством решений или природой возможных решений. В случае Табита он работал с комбинаторикой, чтобы работать над перестановками, необходимыми для победы в шахматной партии. [20]
В дополнение к работе Табита по евклидовой геометрии есть доказательства того, что он был знаком и с геометрией Архимеда . Его работа с коническими сечениями и вычисление формы параболоида ( купол ) показывают его мастерство как архимедова геометра. Это еще больше подчеркивается [ необходимо разъяснение ] использованием Табитом свойства Архимеда для получения элементарного приближения объема параболоида. Использование неравных сечений, хотя и относительно простое, показывает критическое понимание как евклидовой, так и архимедовой геометрии. [21] Табит также был ответственен за комментарий к Liber Assumpta Архимеда . [22]
В физике Табит отверг перипатетические и аристотелевские понятия «естественного места» для каждого элемента . Вместо этого он предложил теорию движения, в которой как восходящие, так и нисходящие движения вызваны весом , и что порядок вселенной является результатом двух конкурирующих притяжений ( jadhb ): одно из них «между подлунными и небесными элементами», а другое — «между всеми частями каждого элемента в отдельности». [23] а в механике он был основателем статики . [24] Кроме того, Liber Karatonis Табита содержал доказательство закона рычага. Эта работа была результатом объединения аристотелевских и архимедовых идей динамики и механики. [11]
Одним из важнейших текстов Курры является его работа с Kitab fi 'l-qarastun . Этот текст состоит из арабской механической традиции. [25] Другим важным текстом является Kitab fi sifat alwazn , в котором обсуждаются концепции равноплечего баланса. Сообщается, что Курра был одним из первых, кто написал о концепции равноплечего баланса или, по крайней мере, систематизировал ее трактовку.
Курра стремился установить связь между силами движения и расстоянием, пройденным мобильным устройством. [25]
Сабит был хорошо известен как врач и написал значительное количество медицинских трактатов и комментариев. Его работы включали общие справочники, такие как al-Dhakhira fī ilm al-tibb («Сокровищница медицины»), Kitāb al-Rawda fi l–tibb («Книга сада медицины») и al-Kunnash («Сборник»). Он также создал специальные работы по таким темам, как желчные камни; лечение таких болезней, как оспа, корь и заболевания глаз; и обсуждал ветеринарию и анатомию птиц. Сабит написал комментарии к работам Галена и других, включая такие работы, как « О растениях» (приписывается Аристотелю , но, вероятно, написана философом первого века до н. э. Николаем Дамасским ). [5]
Один из рассказов о работе Сабита как врача приводится в « Та'рих аль-хукама » Ибн аль-Кифти , где Сабиту приписывают исцеление мясника, который, как предполагалось, должен был непременно умереть. [5]
Лишь немногие произведения Сабита сохранились в первоначальном виде.
Дополнительные работы Табита включают:
В своем кратком изложении « Китаб ихбар аль -'улама' би ахбар аль-хукама» аль-Кифти аль-Заузани перечисляет семь религиозных трудов на сирийском языке Сабита и говорит, что он также писал на сирийском языке о музыке и геометрии. Согласно Бар-Эбрею , сирийскому историку XIII века, Сабит написал около 150 работ на арабском языке и 16 на сирийском. Он утверждает, что сам видел большинство сирийских работ и перечисляет их. Список Бар-Эбрея согласуется со списком аль-Заузани. Большинство работ посвящены языческой религии, но есть работа по музыке и две по геометрии, а также «книга летописи древних сирийских царей, которые являются халдеями» и «книга о славе его расы и его предках, от которых они произошли» [28] .
Секта, имеющая сильные греческие связи, в более ранние времена приняла греческую культуру, и для ее членов было обычным делом говорить по-гречески, хотя после завоевания сабиев исламом они стали арабоговорящими. На юго-востоке Турции был еще один язык, а именно сирийский, который был основан на восточноарамейском диалекте Эдессы. Этот язык был родным языком Табита ибн Курры, но он свободно владел как греческим, так и арабским.
{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )Обзоры: Сейед Хоссейн Наср (1998) в Isis 89 (1) стр. 112-113; Чарльз Бернетт (1998) в Bulletin of the School of Oriental and African Studies, University of London 61 (2) стр. 406.