Метод Хартри-Фока

Метод в квантовой физике

В вычислительной физике и химии метод Хартри –Фока ( HF ) представляет собой метод приближенного определения волновой функции и энергии квантовой системы многих тел в стационарном состоянии .

Метод Хартри–Фока часто предполагает, что точная N -частичная волновая функция системы может быть аппроксимирована одним детерминантом Слейтера (в случае, когда частицы являются фермионами ) или одной постоянной (в случае бозонов ) N спин-орбиталей . Применяя вариационный метод , можно вывести набор N -связанных уравнений для N спин-орбиталей. Решение этих уравнений дает волновую функцию Хартри–Фока и энергию системы. Приближение Хартри–Фока является примером теории среднего поля ^[1] , где пренебрежение флуктуациями более высокого порядка в параметре порядка позволяет заменить члены взаимодействия квадратичными членами, получая точно решаемые гамильтонианы.

Особенно в старой литературе метод Хартри-Фока также называют методом самосогласованного поля ( SCF ). При выводе того, что сейчас называется уравнением Хартри как приближенным решением уравнения Шредингера , Хартри потребовал, чтобы конечное поле, вычисленное из распределения заряда, было «самосогласованным» с предполагаемым начальным полем. Таким образом, самосогласованность была требованием решения. Решения нелинейных уравнений Хартри-Фока также ведут себя так, как будто каждая частица подвергается воздействию среднего поля, созданного всеми другими частицами (см. оператор Фока ниже), и, следовательно, терминология продолжилась. Уравнения почти универсально решаются с помощью итерационного метода , хотя алгоритм итерации с фиксированной точкой не всегда сходится. ^[2] Эта схема решения не является единственно возможной и не является существенной особенностью метода Хартри-Фока.

Метод Хартри–Фока находит свое типичное применение в решении уравнения Шредингера для атомов, молекул, наноструктур ^[3] и твердых тел, но он также нашел широкое применение в ядерной физике . (См. метод Хартри–Фока–Боголюбова для обсуждения его применения в теории структуры ядра ). В теории структуры атома вычисления могут быть для спектра со многими возбужденными уровнями энергии, и, следовательно, метод Хартри–Фока для атомов предполагает, что волновая функция является функцией состояния одной конфигурации с четко определенными квантовыми числами и что уровень энергии не обязательно является основным состоянием .

Как для атомов, так и для молекул решение Хартри-Фока является центральной отправной точкой для большинства методов, которые более точно описывают многоэлектронную систему.

Остальная часть этой статьи будет посвящена приложениям в теории электронной структуры, подходящим для молекул с атомом в качестве особого случая. Здесь обсуждается только ограниченный метод Хартри-Фока, где атом или молекула являются системой с замкнутой оболочкой, где все орбитали (атомные или молекулярные) заняты дважды. Системы с открытой оболочкой , где некоторые электроны не спарены, могут рассматриваться либо ограниченным методом с открытой оболочкой , либо неограниченным методом Хартри-Фока.

Краткая история

Ранние полуэмпирические методы

Метод Хартри–Фока возник в конце 1920-х годов, вскоре после открытия уравнения Шредингера в 1926 году. Методы Дугласа Хартри основывались на некоторых более ранних полуэмпирических методах начала 1920-х годов (Э. Фуэса, Р. Б. Линдсея и его самого), основанных на старой квантовой теории Бора.

В модели атома Бора энергия состояния с главным квантовым числом n задается в атомных единицах как . Из атомных спектров было замечено, что уровни энергии многоэлектронных атомов хорошо описываются путем применения модифицированной версии формулы Бора. Вводя квантовый дефект d в качестве эмпирического параметра, уровни энергии общего атома были хорошо аппроксимированы формулой , в том смысле, что можно было довольно хорошо воспроизвести наблюдаемые уровни переходов, наблюдаемые в рентгеновской области (например, см. эмпирическое обсуждение и вывод в законе Мозли ). Существование ненулевого квантового дефекта было приписано отталкиванию электронов, которое явно не существует в изолированном атоме водорода. Это отталкивание приводило к частичному экранированию голого заряда ядра. Эти ранние исследователи позже ввели другие потенциалы, содержащие дополнительные эмпирические параметры, в надежде на лучшее воспроизведение экспериментальных данных. ${\displaystyle E=-1/n^{2}}$ ${\displaystyle E=-1/(n+d)^{2}}$

метод Хартри

В 1927 году DR Hartree представил процедуру, которую он назвал методом самосогласованного поля, для вычисления приближенных волновых функций и энергий для атомов и ионов. ^[4] Хартри стремился избавиться от эмпирических параметров и решить многочастичное независимое от времени уравнение Шредингера из фундаментальных физических принципов, т. е. ab initio . Его первый предложенный метод решения стал известен как метод Хартри , или произведение Хартри . Однако многие современники Хартри не понимали физических обоснований метода Хартри: многим людям он казался содержащим эмпирические элементы, и его связь с решением многочастичного уравнения Шредингера была неясной. Однако в 1928 году JC Slater и JA Gaunt независимо показали, что метод Хартри можно сформулировать на более прочной теоретической основе, применив вариационный принцип к анзацу (пробной волновой функции) как произведению одночастичных функций. ^{[5] [6]}

В 1930 году Слейтер и В. А. Фок независимо друг от друга указали на то, что метод Хартри не соблюдает принцип антисимметрии волновой функции. ^{[7] [8]} Метод Хартри использовал принцип исключения Паули в его старой формулировке, запрещающий присутствие двух электронов в одном и том же квантовом состоянии. Однако было показано, что это принципиально неполно, поскольку не учитывает квантовую статистику .

Хартри–Фок

Решение проблемы отсутствия антисимметрии в методе Хартри пришло, когда было показано, что определитель Слейтера , определитель одночастичных орбиталей, впервые использованный Гейзенбергом и Дираком в 1926 году, тривиально удовлетворяет антисимметричному свойству точного решения и, следовательно, является подходящим анзацем для применения вариационного принципа . Исходный метод Хартри затем можно рассматривать как приближение к методу Хартри–Фока путем пренебрежения обменом . Исходный метод Фока в значительной степени опирался на теорию групп и был слишком абстрактным для понимания и реализации современными физиками. В 1935 году Хартри переформулировал метод, чтобы он был более подходящим для целей вычислений. ^[9]

Метод Хартри–Фока, несмотря на его физически более точную картину, мало использовался до появления электронных компьютеров в 1950-х годах из-за гораздо больших вычислительных требований по сравнению с ранним методом Хартри и эмпирическими моделями. ^[10] Первоначально и метод Хартри, и метод Хартри–Фока применялись исключительно к атомам, где сферическая симметрия системы позволяла значительно упростить задачу. Эти приближенные методы часто использовались (и используются) вместе с приближением центрального поля , чтобы наложить условие, что электроны в одной и той же оболочке имеют одинаковую радиальную часть, и ограничить вариационное решение спиновой собственной функцией . Тем не менее, вычисление решения вручную с использованием уравнений Хартри–Фока для атома среднего размера было трудоемким; малые молекулы требовали вычислительных ресурсов, намного превышающих те, что были доступны до 1950 года.

Алгоритм Хартри-Фока

Метод Хартри–Фока обычно используется для решения не зависящего от времени уравнения Шредингера для многоэлектронного атома или молекулы, как описано в приближении Борна–Оппенгеймера . Поскольку для многоэлектронных систем не существует известных аналитических решений ( есть решения для одноэлектронных систем, таких как водородные атомы и двухатомный катион водорода ), задача решается численно. Из-за нелинейностей, вносимых приближением Хартри–Фока, уравнения решаются с использованием нелинейного метода, такого как итерация , что и дало название «метод самосогласованного поля».

Приближения

Метод Хартри-Фока делает пять основных упрощений для решения этой задачи:

• Приближение Борна–Оппенгеймера изначально предполагается. Полная молекулярная волновая функция на самом деле является функцией координат каждого из ядер, в дополнение к координатам электронов.
• Обычно релятивистские эффекты полностью игнорируются. Оператор импульса предполагается полностью нерелятивистским.
• Вариационное решение предполагается как линейная комбинация конечного числа базисных функций , которые обычно (но не всегда) выбираются ортогональными . Конечный базисный набор предполагается приблизительно полным .
• Предполагается, что каждая собственная функция энергии может быть описана одним определителем Слейтера , антисимметризированным произведением одноэлектронных волновых функций (т.е. орбиталей ).
• Подразумевается приближение среднего поля . Эффекты, возникающие из-за отклонений от этого предположения, игнорируются. Эти эффекты часто совместно используются в качестве определения термина электронная корреляция . Однако, строго говоря, ярлык «электронная корреляция» охватывает как кулоновскую корреляцию, так и корреляцию Ферми, а последняя является эффектом электронного обмена, который полностью учитывается в методе Хартри-Фока. ^{[11] [12]} Изложенный в этой терминологии, метод игнорирует только кулоновскую корреляцию. Однако это важный недостаток, объясняющий (среди прочего) неспособность Хартри-Фока уловить лондонскую дисперсию . ^[13]

Ослабление последних двух приближений приводит к появлению множества так называемых пост-Хартри-Фоковских методов.

Вариационная оптимизация орбиталей

Алгоритмическая блок-схема, иллюстрирующая метод Хартри–Фока

Вариационная теорема утверждает , что для независимого от времени гамильтониана любая пробная волновая функция будет иметь ожидаемое значение энергии , которое больше или равно истинной волновой функции основного состояния, соответствующей данному гамильтониану. Из-за этого энергия Хартри-Фока является верхней границей истинной энергии основного состояния данной молекулы. В контексте метода Хартри-Фока наилучшим возможным решением является предел Хартри-Фока ; т. е. предел энергии Хартри-Фока, когда базисный набор приближается к полноте . (Другим является предел полного CI , где последние два приближения теории Хартри-Фока, описанные выше, полностью отменены. Только при достижении обоих пределов получается точное решение с точностью до приближения Борна-Оппенгеймера.) Энергия Хартри-Фока является минимальной энергией для одного определителя Слейтера.

Начальной точкой метода Хартри-Фока является набор приближенных одноэлектронных волновых функций, известных как спин-орбитали . Для расчета атомной орбитали это обычно орбитали для водородоподобного атома (атома с одним электроном, но соответствующим зарядом ядра). Для расчета молекулярной орбитали или кристаллического расчета начальные приближенные одноэлектронные волновые функции обычно представляют собой линейную комбинацию атомных орбиталей (ЛКАО).

Орбитали выше учитывают присутствие других электронов только в среднем. В методе Хартри-Фока влияние других электронов учитывается в контексте теории среднего поля . Орбитали оптимизируются, требуя от них минимизировать энергию соответствующего определителя Слейтера. Результирующие вариационные условия на орбиталях приводят к новому одноэлектронному оператору, оператору Фока . Как минимум, занятые орбитали являются собственными решениями оператора Фока через унитарное преобразование между собой. Оператор Фока является эффективным одноэлектронным гамильтоновым оператором, являющимся суммой двух членов. Первый представляет собой сумму операторов кинетической энергии для каждого электрона, энергию межъядерного отталкивания и сумму ядерно-электронных кулоновских членов притяжения. Второй представляет собой кулоновские члены отталкивания между электронами в описании теории среднего поля; чистая энергия отталкивания для каждого электрона в системе, которая вычисляется путем рассмотрения всех других электронов внутри молекулы как гладкого распределения отрицательного заряда. Это основное упрощение, присущее методу Хартри–Фока, и оно эквивалентно пятому упрощению в приведенном выше списке.

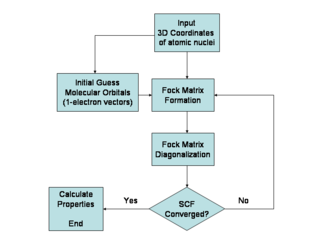
Поскольку оператор Фока зависит от орбиталей, используемых для построения соответствующей матрицы Фока , собственные функции оператора Фока, в свою очередь, являются новыми орбиталями, которые могут быть использованы для построения нового оператора Фока. Таким образом, орбитали Хартри–Фока оптимизируются итеративно до тех пор, пока изменение полной электронной энергии не станет ниже предопределенного порога. Таким образом, вычисляется набор самосогласованных одноэлектронных орбиталей. Электронная волновая функция Хартри–Фока затем является определителем Слейтера, построенным из этих орбиталей. Следуя основным постулатам квантовой механики, волновая функция Хартри–Фока затем может быть использована для вычисления любого желаемого химического или физического свойства в рамках метода Хартри–Фока и используемых приближений.

Математическая формулировка

Вывод

Согласно правилам Слейтера–Кондона , математическое ожидание энергии молекулярного электронного гамильтониана для детерминанта Слейтера равно ${\displaystyle {\hat {H}}^{e}}$

${\textstyle {\begin{aligned}E[\psi ^{HF}]&=\left\langle \psi ^{HF}|{\hat {H}}^{e}|\psi ^{HF}\right\rangle \\&=\sum _{i=1}^{N}\int {\text{d}}\mathbf {x} _{i}\,\phi _{i}^{*}(\mathbf {x} _{i}){\hat {h}}(\mathbf {x} _{i})\phi _{i}(\mathbf {x} _{i})\\&+{\frac {1}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}\int \mathrm {d} \mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{i}^{*}(\mathbf {x} _{i})\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{i}-\mathbf {x} _{j}|}}\phi _{i}(\mathbf {x} _{i})\phi _{j}(\mathbf {x} _{j})\\&-{\frac {1}{2}}\sum _{i=1}^{N}\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{i}^{*}(\mathbf {x} _{i})\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{i}-\mathbf {x} _{j}|}}\phi _{i}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{i})\end{aligned}}}$

где — одноэлектронный оператор, включающий электронные кинетические операторы и электронно-ядерное кулоновское взаимодействие, а также ${\displaystyle {\hat {h}}}$

${\displaystyle {\begin{aligned}\psi ^{HF}=\psi (\mathbf {x} _{1},\mathbf {x} _{2},\ldots ,\mathbf {x} _{N})={\frac {1}{\sqrt {N!}}}{\begin{vmatrix}\phi _{1}(\mathbf {x} _{1})&\phi _{2}(\mathbf {x} _{1})&\cdots &\phi _{N}(\mathbf {x} _{1})\\\phi _{1}(\mathbf {x} _{2})&\phi _{2}(\mathbf {x} _{2})&\cdots &\phi _{N}(\mathbf {x} _{2})\\\vdots &\vdots &\ddots &\vdots \\\phi _{1}(\mathbf {x} _{N})&\phi _{2}(\mathbf {x} _{N})&\cdots &\phi _{N}(\mathbf {x} _{N})\end{vmatrix}}.\end{aligned}}}$

Для вывода уравнения Хартри-Фока мы минимизируем функционал энергии для N электронов с ортонормальными ограничениями.

${\displaystyle \delta E[\phi _{k}^{*}(x_{k})]=\delta \left\langle \psi ^{HF}|{\hat {H}}^{e}|\psi ^{HF}\right\rangle -\delta \left[\sum _{i=1}^{N}\sum _{j=1}^{N}\lambda _{ij}\left(\left\langle \phi _{i},\phi _{j}\right\rangle -\delta _{ij}\right)\right]{\stackrel {!}{=}}\,0,}$

Поскольку мы можем выбрать базис , то выберем такой базис, в котором матрица множителей Лагранжа станет диагональной, т.е. . Выполняя вариацию , получим ${\displaystyle \phi _{i}(x_{i})}$ ${\displaystyle \lambda _{ij}}$ ${\displaystyle \lambda _{ij}=\epsilon _{i}\delta _{ij}}$

${\displaystyle {\begin{aligned}\delta E[\phi _{k}^{*}(x_{k})]&=\sum _{i=1}^{N}\int {\text{d}}\mathbf {x} _{i}\,{\hat {h}}(\mathbf {x} _{i})\phi _{i}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&+\sum _{i=1}^{N}\sum _{j=1}^{N}\int \mathrm {d} \mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{i}-\mathbf {x} _{j}|}}\phi _{i}(\mathbf {x} _{i})\phi _{j}(\mathbf {x} _{j})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&-\sum _{i=1}^{N}\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{i}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{i}-\mathbf {x} _{j}|}}\phi _{i}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&-\sum _{i=1}^{N}\epsilon _{i}\int {\text{d}}\mathbf {x} _{i}\,\phi _{i}(\mathbf {x} _{i})\delta (\mathbf {x} _{i}-\mathbf {x} _{k})\delta _{ik}\\&={\hat {h}}(\mathbf {x} _{k})\phi _{k}(\mathbf {x} _{k})\\&+\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{k}-\mathbf {x} _{j}|}}\phi _{k}(\mathbf {x} _{k})\phi _{j}(\mathbf {x} _{j})\\&-\sum _{j=1}^{N}\int {\text{d}}\mathbf {x} _{j}\phi _{j}^{*}(\mathbf {x} _{j}){\frac {1}{|\mathbf {x} _{k}-\mathbf {x} _{j}|}}\phi _{k}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{k})\\&-\epsilon _{k}\phi _{k}(\mathbf {x} _{k})=0.\\\end{aligned}}}$

Множитель 1/2 в молекулярном гамильтониане выпадает перед двойными интегралами из-за симметрии и правила произведения. Мы можем определить оператор Фока, чтобы переписать уравнение

${\displaystyle {\hat {F}}(\mathbf {x} _{k})\phi _{k}(\mathbf {x} _{k})\equiv \left[{\hat {h}}(\mathbf {x} _{k})+{\hat {J}}(\mathbf {x} _{k})-{\hat {K}}(\mathbf {x} _{k})\right]\phi _{k}(\mathbf {x} _{k})=\epsilon _{k}\phi _{k}(\mathbf {x} _{k}),}$

где оператор Кулона и оператор обмена определяются следующим образом ${\displaystyle {\hat {J}}(\mathbf {x} _{k})}$ ${\displaystyle {\hat {K}}(\mathbf {x} _{k})}$

${\displaystyle {\begin{aligned}{\hat {J}}(\mathbf {x_{k}} )&\equiv \sum _{j=1}^{N}\int \mathrm {d} \mathbf {x} _{j}{\frac {\phi _{j}^{*}(\mathbf {x} _{j})\phi _{j}(\mathbf {x} _{j})}{|\mathbf {x} _{k}-\mathbf {x} _{j}|}}=\sum _{j=1}^{N}\int \mathrm {d} \mathbf {x} _{j}{\frac {\rho (\mathbf {x} _{j})}{|\mathbf {x} _{k}-\mathbf {x} _{j}|}},\\{\hat {K}}(\mathbf {x_{k}} )\phi _{k}(\mathbf {x} _{k})&\equiv \sum _{j=1}^{N}\phi _{j}(\mathbf {x} _{k})\int {\text{d}}\mathbf {x} _{j}{\frac {\phi _{j}^{*}(\mathbf {x} _{j})\phi _{k}(\mathbf {x} _{j})}{|\mathbf {x} _{k}-\mathbf {x} _{j}|}}.\\\end{aligned}}}$

Оператор обмена не имеет классического аналога и может быть определен только как интегральный оператор.

Решение и называются молекулярной орбиталью и орбитальной энергией соответственно. ${\displaystyle \phi _{k}}$ ${\displaystyle \epsilon _{k}}$

Хотя уравнение Хартри-Фока представляется в форме задачи на собственные значения, сам оператор Фока зависит от и должен решаться с помощью другого метода. ${\displaystyle \phi }$

Общая энергия

Оптимальную полную энергию можно записать в терминах молекулярных орбиталей. ${\displaystyle E_{HF}}$

${\displaystyle E_{HF}=\sum _{i=1}^{N}{\hat {h}}_{ii}+\sum _{i=1}^{N}\sum _{j=1}^{N/2}[2{\hat {J}}_{ij}-{\hat {K}}_{ij}]+V_{\text{nucl}}}$

${\displaystyle {\hat {J}}_{ij}}$и являются матричными элементами кулоновского и обменного операторов соответственно, а представляет собой полное электростатическое отталкивание между всеми ядрами в молекуле. ${\displaystyle {\hat {K}}_{ij}}$ ${\displaystyle V_{\text{nucl}}}$

Следует подчеркнуть, что полная энергия не равна сумме орбитальных энергий.

Если атом или молекула имеет замкнутую оболочку , полная энергия согласно методу Хартри-Фока равна

${\displaystyle E_{HF}=2\sum _{i=1}^{N/2}{\hat {h}}_{ii}+\sum _{i=1}^{N/2}\sum _{j=1}^{N/2}[2{\hat {J}}_{ij}-{\hat {K}}_{ij}]+V_{\text{nucl}}.}$^[14]

Линейная комбинация атомных орбиталей

Обычно в современных вычислениях Хартри-Фока волновые функции одного электрона аппроксимируются линейной комбинацией атомных орбиталей . Эти атомные орбитали называются орбиталями слейтеровского типа . Кроме того, очень часто используемые «атомные орбитали» фактически состоят из линейной комбинации одной или нескольких орбиталей гауссовского типа , а не орбиталей слейтеровского типа, в интересах экономии большого количества времени вычислений.

На практике используются различные базисные наборы , большинство из которых состоят из гауссовых функций. В некоторых приложениях для получения набора ортогональных базисных функций применяется метод ортогонализации, такой как процесс Грама–Шмидта . В принципе, это может сэкономить время вычислений, когда компьютер решает уравнения Рутана–Холла , эффективно преобразуя матрицу перекрытия в единичную матрицу . Однако в большинстве современных компьютерных программ для молекулярных вычислений Хартри–Фока эта процедура не выполняется из-за высокой численной стоимости ортогонализации и появления более эффективных, часто разреженных алгоритмов для решения обобщенной задачи собственных значений , примером которой являются уравнения Рутана–Холла .

Численная стабильность

Численная устойчивость может быть проблемой при этой процедуре, и существуют различные способы борьбы с этой нестабильностью. Один из самых основных и общеприменимых называется F-смешиванием или затуханием. При F-смешивании, как только вычисляется волновая функция одного электрона, она не используется напрямую. Вместо этого используется некоторая комбинация этой вычисленной волновой функции и предыдущих волновых функций для этого электрона, наиболее распространенной из которых является простая линейная комбинация вычисленной и непосредственно предшествующей волновой функции. Хитрый трюк, использованный Хартри для атомных расчетов, заключался в увеличении заряда ядра, тем самым сближая все электроны. По мере стабилизации системы это постепенно уменьшалось до правильного заряда. В молекулярных расчетах иногда используется похожий подход, когда сначала вычисляется волновая функция для положительного иона, а затем эти орбитали используются в качестве отправной точки для нейтральной молекулы. Современные молекулярные компьютерные программы Хартри-Фока используют различные методы для обеспечения сходимости уравнений Рутана-Холла.

Слабые стороны, расширения и альтернативы

Из пяти упрощений, описанных в разделе «Алгоритм Хартри–Фока», пятое обычно является наиболее важным. Пренебрежение электронной корреляцией может привести к большим отклонениям от экспериментальных результатов. Было разработано несколько подходов к этой слабости, совместно называемых пост-методами Хартри–Фока , для включения электронной корреляции в многоэлектронную волновую функцию. Один из этих подходов, теория возмущений Мёллера–Плессета , рассматривает корреляцию как возмущение оператора Фока. Другие расширяют истинную многоэлектронную волновую функцию в терминах линейной комбинации детерминант Слейтера, таких как многоконфигурационное самосогласованное поле , конфигурационное взаимодействие , квадратичное конфигурационное взаимодействие и полное активное пространство SCF (CASSCF) . Другие методы (например, вариационный квантовый метод Монте-Карло ) модифицируют волновую функцию Хартри-Фока, умножая ее на корреляционную функцию (фактор «Джастроу»), которая явно является функцией множества электронов, которые нельзя разложить на независимые одночастичные функции.

Альтернативой расчетам Хартри-Фока, используемым в некоторых случаях, является теория функционала плотности , которая рассматривает как обменную, так и корреляционную энергию, хотя и приблизительно. Действительно, часто используются расчеты, которые являются гибридом двух методов — популярная схема B3LYP является одним из таких гибридных функциональных методов. Другой вариант — использовать современные методы валентных связей .

Пакеты программного обеспечения

Список пакетов программного обеспечения, известных для выполнения расчетов Хартри-Фока, в частности для молекул и твердых тел, см. в списке программного обеспечения для квантовой химии и физики твердого тела .

Смотрите также

Ссылки

1. Bruus, Henrik; Flensberg, Karsten (2014). Многочастичная квантовая теория в физике конденсированного состояния: введение (PDF) (Исправленная версия ред.). Oxford New York: Oxford University Press. ISBN 9780198566335.
2. Фрезе Фишер, Шарлотта (1987). "Общая программа Хартри-Фока". Computer Physics Communications . 43 (3): 355–365. Bibcode : 1987CoPhC..43..355F. doi : 10.1016/0010-4655(87)90053-1.
3. Абдулсаттар, Мудар А. (2012). «Инфракрасные и рамановские спектры нанокристаллов сверхрешетки SiGe: исследование теории функционала плотности». J. Appl. Phys. 111 (4): 044306–044306–4. Bibcode :2012JAP...111d4306A. doi : 10.1063/1.3686610 .
4. Хартри, DR (1928). «Волновая механика атома с некулоновским центральным полем». Math. Proc. Camb. Philos. Soc. 24 (1): 111. Bibcode :1928PCPS...24..111H. doi :10.1017/S0305004100011920. S2CID  121520012.
5. Слейтер, Дж. К. (1928). «Самосогласованное поле и структура атомов». Phys. Rev. 32 (3): 339–348. Bibcode :1928PhRv...32..339S. doi :10.1103/PhysRev.32.339.
6. Gaunt, JA (1928). «Теория атомных полей Хартри». Math. Proc. Camb. Philos. Soc. 24 (2): 328–342. Bibcode :1928PCPS...24..328G. doi :10.1017/S0305004100015851. S2CID  119685329.
7. Слейтер, Дж. К. (1930). «Заметка о методе Хартри». Phys. Rev. 35 (2): 210–211. Bibcode :1930PhRv...35..210S. doi :10.1103/PhysRev.35.210.2.
8. Фок, Вирджиния (1930). «Näherungsmethode zur Lösung des quantenmechanischen Mehrkörperproblems». З. Физ. (на немецком языке). 61 (1): 126–148. Бибкод : 1930ZPhy...61..126F. дои : 10.1007/BF01340294. S2CID  125419115. Фок, В. А. (1930).«Самосогласованное поле» mit Austausch für Natrium». Z. Phys. (на немецком языке). 62 (11): 795–805. Bibcode : 1930ZPhy...62..795F. doi : 10.1007/BF01330439. S2CID  120921212.
9. Хартри, DR; Хартри, W. (1935). "Самосогласованное поле с обменом для бериллия". Proc. R. Soc. Lond. A. 150 ( 869): 9. Bibcode :1935RSPSA.150....9H. doi : 10.1098/rspa.1935.0085 .
10. Слейтер, Дж. К. (1951). «Упрощение метода Хартри-Фока». Physical Review . 81 (3): 385–390. Bibcode : 1951PhRv...81..385S. doi : 10.1103/PhysRev.81.385.
11. Хинчлифф, Алан (2000). Моделирование молекулярных структур (2-е изд.). Baffins Lane, Чичестер, Западный Сассекс PO19 1UD, Англия: John Wiley & Sons Ltd. стр. 186. ISBN 0-471-48993-X.{{cite book}}: CS1 maint: location (link)
12. Сабо, А.; Остлунд, Н.С. (1996). Современная квантовая химия . Минеола, Нью-Йорк: Dover Publishing. ISBN 0-486-69186-1.
13. AJ Stone (1996), Теория межмолекулярных сил , Оксфорд: Clarendon Press.
14. Левин, Айра Н. (1991). Квантовая химия (4-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice Hall. стр. 402-3. ISBN 0-205-12770-3 . 

Источники

• Левин, Айра Н. (1991). Квантовая химия (4-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice Hall. стр. 455–544. ISBN 0-205-12770-3.
• Крамер, Кристофер Дж. (2002). Основы вычислительной химии . Чичестер: John Wiley & Sons, Ltd. стр. 153–189. ISBN 0-471-48552-7.
• Сабо, А.; Остлунд, Н.С. (1996). Современная квантовая химия . Минеола, Нью-Йорк: Dover Publishing. ISBN 0-486-69186-1.

Внешние ссылки

• Волновая механика атома с некулоновским центральным полем. Часть II. Некоторые результаты и обсуждение Д. Р. Хартри , Математические труды Кембриджского философского общества, том 24, стр. 111–132, январь 1928 г.
• Введение в теорию молекулярных орбиталей Хартри-Фока, автор К. Дэвид Шеррилл (июнь 2000 г.)
• Теория среднего поля: Хартри-Фок и БКШ в E. Pavarini, E. Koch, J. van den Brink и G. Sawatzky: Квантовые материалы: эксперименты и теория, Юлих 2016, ISBN 978-3-95806-159-0