метрика Шварцшильда

Решение уравнений поля Эйнштейна

В общей теории относительности Эйнштейна метрика Шварцшильда (также известная как решение Шварцшильда ) является точным решением уравнений поля Эйнштейна , которое описывает гравитационное поле вне сферической массы, при условии, что электрический заряд массы, угловой момент массы и универсальная космологическая постоянная равны нулю. Решение является полезным приближением для описания медленно вращающихся астрономических объектов, таких как многие звезды и планеты , включая Землю и Солнце. Оно было найдено Карлом Шварцшильдом в 1916 году.

Согласно теореме Биркгофа , метрика Шварцшильда является наиболее общим сферически симметричным вакуумным решением уравнений поля Эйнштейна. Черная дыра Шварцшильда или статическая черная дыра — это черная дыра , которая не имеет ни электрического заряда, ни углового момента (не вращается). Черная дыра Шварцшильда описывается метрикой Шварцшильда и не может быть отличима от любой другой черной дыры Шварцшильда, кроме как по массе.

Черная дыра Шварцшильда характеризуется окружающей сферической границей, называемой горизонтом событий , которая расположена на радиусе Шварцшильда ( ), часто называемом радиусом черной дыры. Граница не является физической поверхностью, и человек, который упал через горизонт событий (до того, как его разорвали приливные силы), не заметил бы никакой физической поверхности в этом положении; это математическая поверхность, которая имеет значение для определения свойств черной дыры. Любая невращающаяся и незаряженная масса, которая меньше ее радиуса Шварцшильда, образует черную дыру. Решение уравнений поля Эйнштейна справедливо для любой массы M , поэтому в принципе (в рамках общей теории относительности) черная дыра Шварцшильда любой массы могла бы существовать, если бы условия стали достаточно благоприятными для ее образования. ${\displaystyle r_{\text{s}}}$

Вблизи черной дыры Шварцшильда пространство искривляется настолько, что даже световые лучи отклоняются, а очень близкий свет может отклоняться настолько, что он несколько раз обходит вокруг черной дыры. ^{[1] [2] [3]}

Формулировка

Метрика Шварцшильда — это сферически симметричная лоренцева метрика (здесь, с соглашением о сигнатурах (+, -, -, -) ), определенная на (подмножестве) , где — трехмерное евклидово пространство, а — двухсфера. Группа вращений действует на фактор или как вращения вокруг центра , оставляя первый фактор неизменным. Метрика Шварцшильда — это решение уравнений поля Эйнштейна в пустом пространстве, что означает, что оно справедливо только вне гравитирующего тела. То есть для сферического тела радиуса решение справедливо для . Чтобы описать гравитационное поле как внутри, так и вне гравитирующего тела, решение Шварцшильда должно быть согласовано с некоторым подходящим внутренним решением в ⁠ ⁠ , ^[4] таким как внутренняя метрика Шварцшильда . $${\displaystyle \mathbb {R} \times \left(E^{3}-O\right)\cong \mathbb {R} \times (0,\infty )\times S^{2}}$$ ${\displaystyle E^{3}}$ ${\displaystyle S^{2}\subset E^{3}}$ ${\displaystyle \mathrm {SO} (3)=\mathrm {SO} (E^{3})}$ ${\displaystyle E^{3}-O}$ ${\displaystyle S^{2}}$ ${\displaystyle O}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle R}$ ${\displaystyle r>R}$ ${\displaystyle r=R}$

В координатах Шварцшильда метрика Шварцшильда (или, что эквивалентно, линейный элемент для собственного времени ) имеет вид , где — метрика на двух сферах, т.е. ⁠ ​​⁠ . Кроме того, ${\displaystyle (t,r,\theta ,\phi )}$ $${\displaystyle {ds}^{2}=c^{2}\,{d\tau }^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)c^{2}\,dt^{2}-\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}-r^{2}{d\Omega }^{2},}$$ ${\displaystyle {d\Omega }^{2}}$ ${\displaystyle {d\Omega }^{2}=\left(d\theta ^{2}+\sin ^{2}\theta \,d\phi ^{2}\right)}$

• ${\displaystyle d\tau ^{2}}$положительно для времениподобных кривых, в этом случае это собственное время (время, измеренное часами, движущимися вдоль той же мировой линии с пробной частицей ), ${\displaystyle \tau }$
• ${\displaystyle c}$это скорость света ,
• ${\displaystyle t}$есть, для ⁠ ⁠ ${\displaystyle r>r_{\text{s}}}$ , временная координата (измеренная часами, расположенными бесконечно далеко от массивного тела и неподвижными относительно него),
• ${\displaystyle r}$для ⁠ ⁠ ${\displaystyle r>r_{\text{s}}}$ радиальная координата (измеряемая как окружность, деленная на 2π , сферы с центром вокруг массивного тела),
• ${\displaystyle \Omega }$является точкой на двух сферах ⁠ ⁠ ${\displaystyle S^{2}}$ ,
• ${\displaystyle \theta }$ - это коширота ( угол от севера, в радианах ) , определяемая после произвольного выбора оси z , ${\displaystyle \Omega }$
• ${\displaystyle \phi }$- долгота ( также в радианах) вокруг выбранной оси z , а ${\displaystyle \Omega }$
• ${\displaystyle r_{\text{s}}}$— радиус Шварцшильда массивного тела, масштабный коэффициент , который связан с его массой соотношением ⁠ ⁠ , где — гравитационная постоянная . ^[5] ${\displaystyle M}$ ${\displaystyle r_{\text{s}}={2GM}/{c^{2}}}$ ${\displaystyle G}$

Метрика Шварцшильда имеет сингулярность при r = 0 , которая является внутренней сингулярностью кривизны. Она также, по-видимому, имеет сингулярность на горизонте событий r = r _s . В зависимости от точки зрения, метрика, таким образом, определена только на внешней области , только на внутренней области или их несвязном объединении. Однако метрика на самом деле несингулярна поперек горизонта событий, как можно видеть в подходящих координатах (см. ниже). Для ⁠ ⁠ метрика Шварцшильда асимптотически относится к стандартной метрике Лоренца на пространстве Минковского. Для почти всех астрофизических объектов отношение чрезвычайно мало. Например, радиус Шварцшильда Земли примерно равен ${\displaystyle r>r_{\text{s}}}$ ${\displaystyle r<r_{\text{s}}}$ ${\displaystyle r\gg r_{\text{s}}}$ ${\displaystyle {\frac {r_{\text{s}}}{R}}}$ ${\displaystyle r_{\text{s}}^{({\text{Earth}})}}$8,9 мм , в то время как Солнце, которое3,3 × 10 ⁵ раз массивнее ^[6] имеет радиус Шварцшильда около 3,0 км. Отношение становится большим только в непосредственной близости от черных дыр и других сверхплотных объектов, таких как нейтронные звезды . ${\displaystyle r_{\text{s}}^{({\text{Sun}})}}$

Радиальная координата, как оказалось, имеет физическое значение как «надлежащее расстояние между двумя событиями, которые происходят одновременно относительно радиально движущихся геодезических часов, причем два события лежат на одной и той же радиальной координатной линии» ^{[7] .}

Решение Шварцшильда аналогично классической ньютоновской теории гравитации, которая соответствует гравитационному полю вокруг точечной частицы. Даже на поверхности Земли поправки к ньютоновской гравитации составляют всего одну часть на миллиард. ^[8]

История

Решение Шварцшильда названо в честь Карла Шварцшильда , который нашел точное решение в 1915 году и опубликовал его в январе 1916 года, ^[9] чуть больше, чем через месяц после публикации общей теории относительности Эйнштейна. Это было первое точное решение уравнений поля Эйнштейна, отличное от тривиального решения в плоском пространстве . Шварцшильд умер вскоре после публикации своей статьи в результате болезни (предположительно пузырчатки ), которую он развил во время службы в немецкой армии во время Первой мировой войны . ^[10]

Иоганнес Дросте в 1916 году ^[11] независимо получил то же решение, что и Шварцшильд, используя более простой и прямой вывод. ^[12]

В ранние годы общей теории относительности было много путаницы относительно природы сингулярностей, обнаруженных в уравнениях Шварцшильда и других решениях уравнений поля Эйнштейна . В оригинальной статье Шварцшильда он поместил то, что мы сейчас называем горизонтом событий, в начало своей системы координат. В этой статье он также ввел то, что сейчас известно как радиальная координата Шварцшильда ( r в уравнениях выше), в качестве вспомогательной переменной. В своих уравнениях Шварцшильд использовал другую радиальную координату, которая была равна нулю на радиусе Шварцшильда.

Более полный анализ структуры сингулярности был дан Дэвидом Гильбертом ^[13] в следующем году, определив сингулярности как при r = 0, так и при r = r _s . Хотя существовало общее согласие, что сингулярность при r = 0 была «подлинной» физической сингулярностью, природа сингулярности при r = r _s оставалась неясной. ^[14]

В 1921 году Поль Пэнлеве и в 1922 году Альвар Гулльстранд независимо друг от друга создали метрику, сферически симметричное решение уравнений Эйнштейна, которое, как мы теперь знаем, является координатным преобразованием метрики Шварцшильда, координатами Гулльстранда–Пэнлеве , в которых не было сингулярности при r = r _s . Однако они не осознавали, что их решения были просто координатными преобразованиями, и фактически использовали свое решение, чтобы доказать, что теория Эйнштейна была неверной. В 1924 году Артур Эддингтон создал первое координатное преобразование ( координаты Эддингтона–Финкельштейна ), которое показало, что сингулярность при r = r _s была артефактом координат, хотя он также, по-видимому, не осознавал значимости этого открытия. Позже, в 1932 году, Жорж Леметр дал другое преобразование координат ( координаты Лемэтра ) с тем же эффектом и был первым, кто понял, что это подразумевает, что сингулярность при r = r _s не является физической. В 1939 году Говард Робертсон показал, что свободно падающий наблюдатель, спускающийся в метрике Шварцшильда, пересечет сингулярность r = r _s за конечное количество собственного времени, хотя это займет бесконечное количество времени в терминах координатного времени t . ^[14]

В 1950 году Джон Синг опубликовал статью ^[15] , в которой было показано максимальное аналитическое расширение метрики Шварцшильда, снова показав, что сингулярность при r = r _s была артефактом координат и что она представляла два горизонта. Похожий результат позже был заново открыт Джорджем Секерешом ^[16] и независимо Мартином Крускалом ^[17] . Новые координаты, ныне известные как координаты Крускала–Секереша, были намного проще, чем координаты Синга , но обе предоставляли единый набор координат, который охватывал все пространство-время. Однако, возможно, из-за неизвестности журналов, в которых были опубликованы статьи Леметра и Синга, их выводы остались незамеченными, и многие из основных игроков в этой области, включая Эйнштейна, считали, что сингулярность на радиусе Шварцшильда была физической. ^[14] Более поздний вывод Синджем метрического решения Крускала–Секереса ^[18], который был мотивирован желанием избежать «использования «плохих» [Шварцшильда] координат для получения «хороших» [Крускала–Секереса] координат», был в целом недооценен в литературе, но был принят Чандрасекаром в его монографии о черной дыре. ^[19]

Реальный прогресс был достигнут в 1960-х годах, когда математически строгая формулировка, отлитая в терминах дифференциальной геометрии , вошла в область общей теории относительности, что позволило более точно определить, что означает для лоренцева многообразия быть сингулярным. Это привело к окончательной идентификации сингулярности r = r _s в метрике Шварцшильда как горизонта событий , т. е. гиперповерхности в пространстве-времени, которую можно пересечь только в одном направлении. ^[14]

Сингулярности и черные дыры

Решение Шварцшильда, по-видимому, имеет сингулярности при r = 0 и r = r _s ; некоторые компоненты метрики «взрываются» (влекут деление на ноль или умножение на бесконечность) на этих радиусах. Поскольку ожидается, что метрика Шварцшильда будет верна только для радиусов, больших радиуса R гравитирующего тела, то проблем не возникает, пока R > r _s . Для обычных звезд и планет это всегда так. Например, радиус Солнца приблизительно равен700 000  км , тогда как его радиус Шварцшильда составляет всего3 км .

Сингулярность при r = r _s делит координаты Шварцшильда на два несвязанных участка . Внешнее решение Шварцшильда с r > r _s связано с гравитационными полями звезд и планет. Внутреннее решение Шварцшильда с 0 ≤ r < r _s , которое содержит сингулярность при r = 0 , полностью отделено от внешнего участка сингулярностью при r = r _s . Таким образом, координаты Шварцшильда не дают физической связи между двумя участками, которые можно рассматривать как отдельные решения. Однако сингулярность при r = r _s является иллюзией; это пример того, что называется координатной сингулярностью . Как следует из названия, сингулярность возникает из-за плохого выбора координат или координатных условий . При переходе к другой системе координат (например , координатам Леметра , Эддингтона–Финкельштейна , Крускала–Секереша , Новикова или Гулльстранда–Пенлеве ) метрика становится регулярной при r = r _s и может расширить внешний патч до значений r меньших, чем r _s . Используя другое преобразование координат, можно затем связать расширенный внешний патч с внутренним патчем. ^[20]

Однако случай r = 0 отличается. Если кто-то попросит, чтобы решение было действительным для всех r, он столкнется с истинной физической сингулярностью, или гравитационной сингулярностью , в начале координат. Чтобы увидеть, что это истинная сингулярность, нужно рассмотреть величины, которые не зависят от выбора координат. Одной из таких важных величин является инвариант Кречмана , который задается как

${\displaystyle R^{\alpha \beta \gamma \delta }R_{\alpha \beta \gamma \delta }={\frac {12r_{\mathrm {s} }^{2}}{r^{6}}}={\frac {48G^{2}M^{2}}{c^{4}r^{6}}}\,.}$

При r = 0 кривизна становится бесконечной, что указывает на наличие сингулярности. В этой точке метрика не может быть расширена гладко (инвариант Кречмана включает вторые производные метрики), само пространство-время тогда уже не является хорошо определенным. Более того, Сбирски ^[21] показал, что метрика не может быть расширена даже непрерывным образом. Долгое время считалось, что такое решение нефизично. Однако более глубокое понимание общей теории относительности привело к осознанию того, что такие сингулярности являются общей чертой теории, а не просто экзотическим частным случаем.

Решение Шварцшильда, считающееся справедливым для всех r > 0 , называется черной дырой Шварцшильда . Это совершенно справедливое решение уравнений поля Эйнштейна, хотя (как и другие черные дыры) оно обладает довольно странными свойствами. При r < r _s радиальная координата Шварцшильда r становится времениподобной , а временная координата t становится пространственноподобной . ^[22] Кривая при постоянном r больше не является возможной мировой линией частицы или наблюдателя, даже если приложить силу, чтобы попытаться удержать ее там; это происходит из-за того, что пространство-время искривилось настолько, что направление причины и следствия (будущий световой конус частицы ) указывает на сингулярность. ^{[ требуется ссылка ]} Поверхность r = r _s разграничивает то, что называется горизонтом событий черной дыры. Она представляет собой точку, за которой свет больше не может покинуть гравитационное поле. Любой физический объект, радиус которого R становится меньше или равен радиусу Шварцшильда, претерпел гравитационный коллапс и стал черной дырой.

Альтернативные координаты

Решение Шварцшильда может быть выражено в диапазоне различных вариантов выбора координат, помимо координат Шварцшильда, использованных выше. Различные варианты выбора, как правило, подчеркивают различные особенности решения. В таблице ниже показаны некоторые популярные варианты выбора.

В таблице выше для краткости введены некоторые сокращения. Скорость света c установлена ​​на единицу . Обозначение

${\displaystyle g_{\Omega }=d\theta ^{2}+\sin ^{2}\theta \,d\varphi ^{2}}$

используется для метрики единичного радиуса двумерной сферы. Более того, в каждой записи R и T обозначают альтернативные варианты радиальной и временной координаты для конкретных координат. Обратите внимание, что R или T могут различаться от записи к записи.

Координаты Крускала–Секереша имеют вид, к которому можно применить преобразование Белинского–Захарова . Это означает, что черная дыра Шварцшильда является формой гравитационного солитона .

Параболоид Фламма

График параболоида Фламма. Его не следует путать с не связанной с ним концепцией гравитационного колодца .

Пространственная кривизна решения Шварцшильда для r > r _s может быть визуализирована, как показано на графике. Рассмотрим экваториальный срез H с постоянным временем через решение Шварцшильда, зафиксировав θ = ⁠ π/2⁠ , t = константа, и позволяя оставшимся координатам Шварцшильда ( r , φ ) изменяться. Представьте теперь, что есть дополнительное евклидово измерение w , которое не имеет физической реальности (оно не является частью пространства-времени). Затем замените плоскость ( r , φ ) поверхностью, ямочкой в ​​направлении w согласно уравнению ( параболоид Фламма )

${\displaystyle w=2{\sqrt {r_{\mathrm {s} }\left(r-r_{\mathrm {s} }\right)}}.}$

Эта поверхность обладает тем свойством, что расстояния, измеренные внутри нее, соответствуют расстояниям в метрике Шварцшильда, поскольку с учетом определения w выше,

${\displaystyle dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}={\frac {dr^{2}}{1-{\frac {r_{\mathrm {s} }}{r}}}}+r^{2}\,d\varphi ^{2}=-ds^{2}}$

Таким образом, параболоид Фламма полезен для визуализации пространственной кривизны метрики Шварцшильда. Однако его не следует путать с гравитационным колодцем . Ни одна обычная (массивная или безмассовая) частица не может иметь мировую линию, лежащую на параболоиде, поскольку все расстояния на нем являются пространственноподобными (это поперечное сечение в один момент времени, поэтому любая движущаяся по нему частица будет иметь бесконечную скорость ). Тахион может иметь пространственноподобную мировую линию, которая полностью лежит на одном параболоиде. Однако даже в этом случае его геодезический путь не является траекторией, которую можно получить через аналогию гравитационного колодца с «резиновым листом»: в частности, если углубление нарисовано направленным вверх, а не вниз, геодезический путь тахиона все равно искривляется к центральной массе, а не от нее. См. статью о гравитационном колодце для получения дополнительной информации.

Параболоид Фламма может быть получен следующим образом. Евклидова метрика в цилиндрических координатах ( r , φ , w ) записывается как

${\displaystyle -ds^{2}=dw^{2}+dr^{2}+r^{2}\,d\varphi ^{2}\,.}$

Если поверхность описывать функцией w = w ( r ) , то евклидову метрику можно записать как

${\displaystyle -ds^{2}=\left(1+\left({\frac {dw}{dr}}\right)^{2}\right)\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

Сравнивая это с метрикой Шварцшильда в экваториальной плоскости ( θ = ⁠π/2⁠ ) ​​в фиксированное время ( t = константа, dt = 0 )

${\displaystyle -ds^{2}=\left(1-{\frac {r_{\mathrm {s} }}{r}}\right)^{-1}\,dr^{2}+r^{2}\,d\varphi ^{2}\,,}$

дает интегральное выражение для w ( r ) :

${\displaystyle w(r)=\int {\frac {dr}{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}}=2r_{\mathrm {s} }{\sqrt {{\frac {r}{r_{\mathrm {s} }}}-1}}+{\mbox{constant}}}$

решением которого является параболоид Фламма.

Орбитальное движение

Сравнение орбиты тестовой частицы в ньютоновском (слева) и шварцшильдовском (справа) пространстве-времени; обратите внимание на прецессию линии апсид справа.

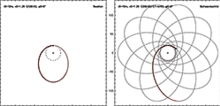
Частица, вращающаяся в метрике Шварцшильда, может иметь устойчивую круговую орбиту с r > 3 r _s . Круговые орбиты с r между 1,5 r _s и 3 r _s нестабильны, и для r < 1,5 r _s круговых орбит не существует . Круговая орбита с минимальным радиусом 1,5 r _s соответствует орбитальной скорости, приближающейся к скорости света. Частица может иметь постоянное значение r между r _s и 1,5 r _s , но только если действует некоторая сила, удерживающая ее там.

Некруговые орбиты, такие как орбита Меркурия , задерживаются на малых радиусах дольше, чем можно было бы ожидать в ньютоновской гравитации . Это можно рассматривать как менее экстремальную версию более драматичного случая, в котором частица проходит через горизонт событий и остается внутри него навсегда. Промежуточные между случаем Меркурия и случаем падения объекта за горизонт событий, существуют экзотические возможности, такие как орбиты с острым краем, в которых спутник может быть вынужден совершать произвольно большое количество почти круговых орбит, после чего он улетает обратно наружу.

Симметрии

Группа изометрий метрики Шварцшильда — это ⁠ ⁠ ${\displaystyle \mathbb {R} \times \mathrm {O} (3)\times \{\pm 1\}}$ , где — ортогональная группа вращений и отражений в трех измерениях, включает временные переносы, а — группа, порожденная обращением времени. ${\displaystyle \mathrm {O} (3)}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \{\pm 1\}}$

Таким образом, это подгруппа десятимерной группы Пуанкаре , которая принимает ось времени (траекторию звезды) в себя. Она опускает пространственные переносы (три измерения) и усиления (три измерения). Она сохраняет временные переносы (одно измерение) и вращения (три измерения). Таким образом, она имеет четыре измерения. Как и группа Пуанкаре, она имеет четыре связанных компонента: компонент тождества; компонент, обращенный во времени; компонент пространственной инверсии; и компонент, который одновременно обращен во времени и пространственно инвертирован.

Кривизны

Скаляр кривизны Риччи и тензор кривизны Риччи оба равны нулю. Ненулевые компоненты тензора кривизны Римана определяются как ^[25]

${\displaystyle -R^{t}{}_{rtr}=2R^{\theta }{}_{r\theta r}=2R^{\phi }{}_{r\phi r}={\frac {r_{\text{s}}}{r^{2}(r_{\text{s}}-r)}},}$

${\displaystyle 2R^{t}{}_{\theta t\theta }=2R^{r}{}_{\theta r\theta }=-R^{\phi }{}_{\theta \phi \theta }=-{\frac {r_{\text{s}}}{r}},}$

${\displaystyle 2R^{t}{}_{\phi t\phi }=2R^{r}{}_{\phi r\phi }=-R^{\theta }{}_{\phi \theta \phi }=-{\frac {r_{\text{s}}\sin ^{2}(\theta )}{r}},}$

${\displaystyle R^{r}{}_{trt}=-2R^{\theta }{}_{t\theta t}=-2R^{\phi }{}_{t\phi t}=c^{2}{\frac {r_{\text{s}}(r_{\text{s}}-r)}{r^{4}}},}$

из чего можно увидеть, что . Шесть из этих формул являются уравнением 5.13 в Кэрролле ^[26] и подразумевают остальные 6 с помощью . Компоненты, которые могут быть получены с помощью других симметрий тензора Римана, не отображаются. ${\displaystyle R^{\gamma }{}_{\alpha \gamma \beta }=0}$ ${\displaystyle R^{\alpha }{}_{\beta \gamma \delta }=g^{\alpha \kappa }g_{\beta \lambda }R^{\lambda }{}_{\kappa \delta \gamma }}$

Для понимания физического смысла этих величин полезно выразить тензор кривизны в ортонормированном базисе. В ортонормированном базисе наблюдателя ненулевые компоненты в геометрических единицах равны ^[25]

${\displaystyle R^{\hat {r}}{}_{{\hat {t}}{\hat {r}}{\hat {t}}}=-R^{\hat {\theta }}{}_{{\hat {\phi }}{\hat {\theta }}{\hat {\phi }}}=-{\frac {r_{\text{s}}}{r^{3}}},}$

${\displaystyle R^{\hat {\theta }}{}_{{\hat {t}}{\hat {\theta }}{\hat {t}}}=R^{\hat {\phi }}{}_{{\hat {t}}{\hat {\phi }}{\hat {t}}}=-R^{\hat {r}}{}_{{\hat {\theta }}{\hat {r}}{\hat {\theta }}}=-R^{\hat {r}}{}_{{\hat {\phi }}{\hat {r}}{\hat {\phi }}}={\frac {r_{\text{s}}}{2r^{3}}}.}$

Опять же, компоненты, которые можно получить с помощью симметрий тензора Римана, не отображаются. Эти результаты инвариантны к любому усилению Лоренца, поэтому компоненты не меняются для нестатичных наблюдателей. Уравнение геодезического отклонения показывает, что приливное ускорение между двумя наблюдателями, разделенными расстоянием , равно , поэтому тело длиной растягивается в радиальном направлении кажущимся ускорением и сжимается в перпендикулярных направлениях . ${\displaystyle \xi ^{\hat {j}}}$ ${\displaystyle D^{2}\xi ^{\hat {j}}/D\tau ^{2}=-R^{\hat {j}}{}_{{\hat {t}}{\hat {k}}{\hat {t}}}\xi ^{\hat {k}}}$ ${\displaystyle L}$ ${\displaystyle (r_{\text{s}}/r^{3})c^{2}L}$ ${\displaystyle -(r_{\text{s}}/(2r^{3}))c^{2}L}$

Смотрите также

• Вывод решения Шварцшильда
• Метрика Рейсснера–Нордстрема (заряженное, невращающееся решение)
• Метрика Керра (незаряженный вращающийся раствор)
• Метрика Керра–Ньюмена (заряженное вращающееся решение)
• Черная дыра , общий обзор
• Координаты Шварцшильда
• Координаты Крускала – Секереса
• Координаты Эддингтона–Финкельштейна
• Координаты Гулстранд – Пенлеве
• Координаты Леметра (решение Шварцшильда в синхронных координатах )
• Поля отсчета в общей теории относительности (наблюдатели Леметра в вакууме Шварцшильда)
• Уравнение Толмена–Оппенгеймера–Волкова (метрические и уравнения давления статического и сферически симметричного тела из изотропного материала)
• Длина Планка

Примечания

1. Люмине, Ж.-П. (1979-05-01). «Изображение сферической черной дыры с тонким аккреционным диском». Астрономия и астрофизика . 75 : 228–235. Bibcode :1979A&A....75..228L. ISSN  0004-6361.
2. Bozza, V. (2002-11-22). "Гравитационное линзирование в пределе сильного поля". Physical Review D. 66 ( 10): 103001. arXiv : gr-qc/0208075 . Bibcode : 2002PhRvD..66j3001B. doi : 10.1103/PhysRevD.66.103001. S2CID  119476658.
3. Снеппен, Альберт (2021-07-09). "Расходящиеся отражения вокруг фотонной сферы черной дыры". Scientific Reports . 11 (1): 14247. Bibcode :2021NatSR..1114247S. doi :10.1038/s41598-021-93595-w. ISSN  2045-2322. PMC 8270963 . PMID  34244573. 
4. Фролов, Валерий; Зельников, Андрей (2011). Введение в физику черных дыр . Оксфорд. стр. 168. ISBN 978-0-19-969229-3.
5. (Ландау и Лифтшиц 1975) . harv error: no target: CITEREFLandauLiftshitz1975 (help)
6. Tennent, RM, ред. (1971). Science Data Book . Oliver & Boyd . ISBN 0-05-002487-6.
7. Готро, Рональд; Хоффманн, Банеш (1978-05-15). «Радиальная координата Шварцшильда как мера собственного расстояния». Physical Review D. 17 ( 10): 2552–2555. Bibcode : 1978PhRvD..17.2552G. doi : 10.1103/PhysRevD.17.2552. ISSN  0556-2821.
8. Элерс, Юрген (январь 1997 г.). "Примеры ньютоновских пределов релятивистского пространства-времени" (PDF) . Классическая и квантовая гравитация . 14 (1A): A119–A126. Bibcode :1997CQGra..14A.119E. doi :10.1088/0264-9381/14/1A/010. hdl : 11858/00-001M-0000-0013-5AC5-F . S2CID  250804865.
9. Шварцшильд, К. (1916). «Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189–196. Бибкод : 1916SPAW.......189S.Перевод см. в Antoci, S.; Loinger, A. (1999). «О гравитационном поле материальной точки согласно теории Эйнштейна». arXiv : physics/9905030 .
10. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Карл Шварцшильд», Архив истории математики Мактьютора , Университет Сент-Эндрюс
11. Дросте, Дж. (1917). «Поле одного центра в теории гравитации Эйнштейна и движение частицы в этом поле» (PDF) . Труды Королевской Нидерландской академии искусств и наук . 19 (1): 197–215. Bibcode : 1917KNAB...19..197D.
12. Kox, AJ (1992). "Общая теория относительности в Нидерландах: 1915–1920". В Eisenstaedt, J.; Kox, AJ (ред.). Исследования по истории общей теории относительности . Birkhäuser . стр. 41. ISBN 978-0-8176-3479-7.
13. Гильберт, Дэвид (1924). «Основы физики». Математические Аннален . 92 (1–2). Спрингер-Верлаг: 1–32. дои : 10.1007/BF01448427. S2CID  179177367.
14. Эрман, Дж. (1999). "Теоремы Пенроуза–Хокинга о сингулярности: история и последствия". В Goenner, H. (ред.). Расширяющиеся миры общей теории относительности . Биркхойзер . стр. 236-. ISBN 978-0-8176-4060-6.
15. Синг, Дж. Л. (1950). «Гравитационное поле частицы». Труды Королевской Ирландской Академии . 53 (6): 83–114. doi :10.1038/164148b0. PMID  18210531. S2CID  4108538.
16. Szekeres, G. (1960). "О сингулярностях риманова многообразия". Publicationes Mathematicae Debrecen . 7 : 285. Bibcode :2002GReGr..34.2001S. doi :10.1023/A:1020744914721. S2CID  118200205.
17. Kruskal, MD (1960). «Максимальное расширение метрики Шварцшильда». Physical Review . 119 (5): 1743–1745. Bibcode : 1960PhRv..119.1743K. doi : 10.1103/PhysRev.119.1743.
18. Synge, JL (декабрь 1974 г.). «Модель вселенных со сферической симметрией». Аннали ди Математика Pura ed Applicata . 98 (1): 239–255. дои : 10.1007/BF02414024. ISSN  0373-3114.
19. Чандрасекар, Субраманьян (2009). Математическая теория черных дыр . Классические тексты Оксфорда по физическим наукам (Переиздание). Оксфорд: Clarendon Press. ISBN 978-0-19-850370-5.
20. Хьюстон, Л. П.; Тод, К. П. (1990). Введение в общую теорию относительности . Cambridge University Press . Глава 19. ISBN 978-0-521-33943-8.
21. Сбирски, Ян (2015). « C ⁰ -нерасширяемость пространства-времени Шварцшильда и пространственноподобный диаметр в лоренцевой геометрии». arXiv : 1507.00601 [gr-qc].
22. Время: Путеводитель путешественника . Oxford University Press, Incorporated. 1999. ISBN 9780199929924. Если посмотреть на черные дыры, то метрика внутри горизонта событий меняет пространственноподобные и временноподобные координаты. Радиус начинает вести себя как времениподобный, а время начинает вести себя как пространствоподобный.
23. Ni, Wei-Tou, ред. (26 мая 2017 г.). Сто лет общей теории относительности: от генезиса и эмпирических оснований до гравитационных волн, космологии и квантовой гравитации. Том 1. World Scientific. стр. I-126. ISBN 9789814635141.
24. Эддингтон, А.С. (1924). Математическая теория относительности (2-е изд.). Cambridge University Press . стр. 93.
25. Мизнер, Чарльз В .; Торн, Кип С.; Уилер , Джон Арчибальд (1973). Гравитация . Нью-Йорк: WH Freeman. ISBN 978-0-7167-0334-1.
26. Кэрролл, Шон (2004). Пространство-время и геометрия: Введение в общую теорию относительности . Эддисон Уэсли. ISBN 0-8053-8732-3.

Ссылки

• Шварцшильд, К. (1916). «Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 7 : 189–196. Бибкод : 1916AbhKP1916..189S.

• Текст оригинальной статьи в Викиресурсе
• Перевод: Antoci, S.; Loinger, A. (1999). «О гравитационном поле материальной точки согласно теории Эйнштейна». arXiv : physics/9905030 .
• Комментарий к статье, дающий более простой вывод: Бел, Л. (2007). «Über das Gravitationsfeld eines Massenpunktesnach der Einsteinschen Theorie». arXiv : 0709.2257 [gr-qc].

• Шварцшильд, К. (1916). «Über das Gravitationsfeld einer Kugel aus incompressible Flüssigkeit». Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften . 1 : 424.

• Текст оригинальной статьи в Викиресурсе
• Перевод: Antoci, S. (1999). «О гравитационном поле сферы несжимаемой жидкости согласно теории Эйнштейна». arXiv : physics/9912033 .

• Фламм, Л. (1916). «Beiträge zur Эйнштейна теории гравитации». Physikalische Zeitschrift . 17 : 448.
• Адлер, Р.; Базен, М.; Шиффер, М. (1975). Введение в общую теорию относительности (2-е изд.). McGraw-Hill . Глава 6. ISBN 0-07-000423-4.
• Ландау, Л. Д.; Лифшиц, Э. М. (1951). Классическая теория полей . Курс теоретической физики . Том 2 (4-е пересмотренное английское издание). Pergamon Press . Глава 12. ISBN 0-08-025072-6.
• Misner, CW; Thorne, KS; Wheeler, JA (1970). Гравитация . WH Freeman . Главы 31 и 32. ISBN 0-7167-0344-0.
• Вайнберг, С. (1972). Гравитация и космология: принципы и приложения общей теории относительности . John Wiley & Sons . Глава 8. ISBN 0-471-92567-5.
• Тейлор, Э. Ф.; Уилер, Дж. А. (2000). Исследование черных дыр: Введение в общую теорию относительности . Эддисон-Уэсли . ISBN 0-201-38423-X.
• Heinzle, JM; Steinbauer, R. (2002). «Замечания о распределительной геометрии Шварцшильда». Журнал математической физики . 43 (3): 1493–1508. arXiv : gr-qc/0112047 . Bibcode :2002JMP....43.1493H. doi :10.1063/1.1448684. S2CID  119677857.