Тензор кривизны Римана

В математической области дифференциальной геометрии тензор кривизны Римана или тензор Римана-Кристофеля (в честь Бернхарда Римана и Элвина Бруно Кристоффеля ) является наиболее распространенным способом выражения кривизны римановых многообразий . Он ставит в соответствие тензор каждой точке риманова многообразия (т. е. является тензорным полем ). Это локальный инвариант римановой метрики, который измеряет неспособность вторых ковариантных производных коммутировать. Риманово многообразие имеет нулевую кривизну тогда и только тогда, когда оно плоское , т. е. локально изометрично евклидову пространству . ^[1] Тензор кривизны также может быть определен для любого псевдориманова многообразия или любого многообразия, снабженного аффинной связностью .

Это центральный математический инструмент в теории общей относительности , современной теории гравитации , а кривизну пространства-времени в принципе можно наблюдать с помощью уравнения геодезического отклонения . Тензор кривизны представляет собой приливную силу, испытываемую твердым телом, движущимся по геодезической , в смысле, уточненном уравнением Якоби .

Определение

Пусть ( M , g) — риманово или псевдориманово многообразие и — пространство всех векторных полей на M. Определим тензор кривизны Римана как отображение по следующей формуле ^[2] где — связность Леви-Чивита : ${\mathfrak {X}}(M)$ ${\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\times {\mathfrak {X}}(M)\rightarrow {\mathfrak {X}}(M)$ $\nabla$

R(X,Y)Z=\nabla _{X}\nabla _{Y}Z-\nabla _{Y}\nabla _{X}Z-\nabla _{[X,Y]}Z

или эквивалентно

R(X,Y)=[\nabla _{X},\nabla _{Y}]-\nabla _{[X,Y]}

где [ X , Y ] — скобка Ли векторных полей и коммутатор дифференциальных операторов. Оказывается, что правая часть на самом деле зависит только от значения векторных полей в данной точке, что примечательно, поскольку ковариантная производная векторного поля также зависит от значений поля в окрестности точки. Следовательно, – -тензорное поле. При фиксированном линейное преобразование также называют преобразованием кривизны или эндоморфизмом . Иногда тензор кривизны определяется с противоположным знаком. $[\nabla _{X},\nabla _{Y}]$ $X,Y,Z$ $R$ $(1,3)$ $X,Y$ $Z\mapsto R(X,Y)Z$

Тензор кривизны измеряет некоммутативность ковариантной производной и, как таковой, является препятствием интегрируемости для существования изометрии с евклидовым пространством (называемым в этом контексте плоским пространством).

Поскольку соединение Леви-Чивита не имеет кручения, кривизну также можно выразить через вторую ковариантную производную ^[3]

{\textstyle \nabla _{X,Y}^{2}Z=\nabla _{X}\nabla _{Y}Z-\nabla _{\nabla _{X}Y}Z}

как

R(X,Y)=\nabla _{X,Y}^{2}-\nabla _{Y,X}^{2}

Таким образом, тензор кривизны измеряет некоммутативность второй ковариантной производной. В абстрактной индексной записи

R^{d}{}_{cab}Z^{c}=\nabla _{a}\nabla _{b}Z^{d}-\nabla _{b}\nabla _{a}Z^{d}.

коммутатором^[4]^[5]

A_{\nu }

A_{\nu ;\rho \sigma }-A_{\nu ;\sigma \rho }=A_{\beta }R^{\beta }{}_{\nu \rho \sigma }.

Эту формулу часто называют тождеством Риччи . ^[6] Это классический метод, использованный Риччи и Леви-Чивитой для получения выражения для тензора кривизны Римана. ^[7] Это тождество можно обобщить, чтобы получить коммутаторы для двух ковариантных производных произвольных тензоров следующим образом ^[8]

{\begin{aligned}&\nabla _{\delta }\nabla _{\gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}-\nabla _{\gamma }\nabla _{\delta }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}\\[3pt]={}&R^{\alpha _{1}}{}_{\rho \delta \gamma }T^{\rho \alpha _{2}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s}}+\ldots +R^{\alpha _{r}}{}_{\rho \delta \gamma }T^{\alpha _{1}\cdots \alpha _{r-1}\rho }{}_{\beta _{1}\cdots \beta _{s}}-R^{\sigma }{}_{\beta _{1}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\sigma \beta _{2}\cdots \beta _{s}}-\ldots -R^{\sigma }{}_{\beta _{s}\delta \gamma }T^{\alpha _{1}\cdots \alpha _{r}}{}_{\beta _{1}\cdots \beta _{s-1}\sigma }\end{aligned}}

Эта формула без изменений применима и к тензорным плотностям , поскольку для связи Леви-Чивита ( не родовой ) получается: ^[6]

\nabla _{\mu }\left({\sqrt {g}}\right)\equiv \left({\sqrt {g}}\right)_{;\mu }=0,

где

g=\left|\det \left(g_{\mu \nu }\right)\right|.

Иногда удобно также определить чисто ковариантную версию тензора кривизны как

R_{\rho \sigma \mu \nu }=g_{\rho \zeta }R^{\zeta }{}_{\sigma \mu \nu }.

Геометрический смысл

Неофициально

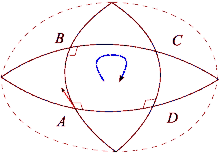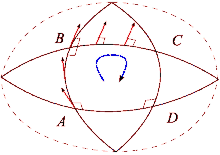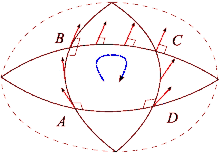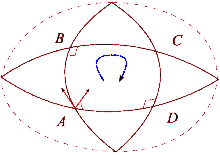
Эффект искривления пространства можно увидеть, сравнив теннисный корт и Землю. Начните с правого нижнего угла теннисного корта, держа ракетку на севере. Затем, прогуливаясь по контуру корта, на каждом шагу следите за тем, чтобы теннисная ракетка сохраняла ту же ориентацию, параллельную ее предыдущему положению. После завершения цикла теннисная ракетка будет параллельна исходному исходному положению. Это потому, что теннисные корты построены с ровной поверхностью. С другой стороны, поверхность Земли искривлена: мы можем совершить петлю на поверхности Земли. Начиная с экватора, направьте теннисную ракетку на север вдоль поверхности Земли. Опять же, теннисная ракетка всегда должна оставаться параллельной своему предыдущему положению, используя в качестве ориентира местную плоскость горизонта. Для этого пути сначала идите к северному полюсу, затем идите боком (т. е. не поворачивая) вниз к экватору и, наконец, идите назад к исходной позиции. Теперь теннисная ракетка будет направлена на запад, хотя в начале пути она указывала на север и вы ни разу не повернули свое тело. Этот процесс похож на параллельную транспортировку вектора по пути, и разница определяет, почему линии, которые кажутся «прямыми», являются «прямыми» только локально. Каждый раз, когда круг завершается, теннисная ракетка будет отклоняться дальше от исходного положения на величину, зависящую от расстояния и кривизны поверхности. Можно определить пути вдоль изогнутой поверхности, где параллельный транспорт работает так же, как и на плоском пространстве. Это геодезические пространства, например любой сегмент большого круга сферы.

Понятие искривленного пространства в математике отличается от разговорного употребления. Например, если бы описанный выше процесс был завершен на цилиндре, можно было бы обнаружить, что он не искривлен в целом, поскольку кривизна вокруг цилиндра компенсируется плоскостностью вдоль цилиндра, это является следствием гауссовой кривизны и теоремы Гаусса Egregium . Знакомый пример — гибкий кусок пиццы, который останется жестким по всей длине, если его изогнуть по ширине.

Тензор кривизны Римана — это способ измерить внутреннюю кривизну. Когда вы записываете его в терминах его компонентов (например, записываете компоненты вектора), он состоит из многомерного массива сумм и произведений частных производных (некоторые из этих частных производных можно рассматривать как своего рода запись кривизна, возникающая у человека, идущего по прямой линии на изогнутой поверхности).

Формально

Когда вектор в евклидовом пространстве перемещается параллельно по петле, он снова будет указывать в исходном направлении после возвращения в исходное положение. Однако в общем случае это свойство не выполняется. Тензор кривизны Римана непосредственно измеряет несостоятельность этого в общем римановом многообразии . Эта ошибка известна как неголономность многообразия .

Пусть – кривая риманова многообразия . Обозначим через параллельное транспортное отображение вдоль . Параллельные транспортные карты связаны с ковариантной производной соотношением $x_{t}$ $M$ $\tau _{x_{t}}:T_{x_{0}}M\to T_{x_{t}}M$ $x_{t}$

\nabla _{{\dot {x}}_{0}}Y=\lim _{h\to 0}{\frac {1}{h}}\left(Y_{x_{0}}-\tau _{x_{h}}^{-1}\left(Y_{x_{h}}\right)\right)=\left.{\frac {d}{dt}}\left(\tau _{x_{t}}^{-1}(Y_{x_{t}})\right)\right|_{t=0}

для каждого векторного поля , определенного вдоль кривой. $Y$

Предположим, что и — пара коммутирующих векторных полей. Каждое из этих полей порождает однопараметрическую группу диффеоморфизмов в окрестности точки . Обозначим через и соответственно параллельные переносы по потокам и за время . Параллельный перенос вектора вокруг четырехугольника со сторонами , , , определяется выражением $X$ $Y$ $x_{0}$ $\tau _{tX}$ $\tau _{tY}$ $X$ $Y$ $t$ $Z\in T_{x_{0}}M$ $tY$ $sX$ $-tY$ $-sX$

\tau _{sX}^{-1}\tau _{tY}^{-1}\tau _{sX}\tau _{tY}Z.

Это измеряет неспособность параллельного транспорта вернуться в исходное положение в касательном пространстве . Сокращение цикла путем отправки дает бесконечно малое описание этого отклонения: $Z$ $T_{x_{0}}M$ $s,t\to 0$

\left.{\frac {d}{ds}}{\frac {d}{dt}}\tau _{sX}^{-1}\tau _{tY}^{-1}\tau _{sX}\tau _{tY}Z\right|_{s=t=0}=\left(\nabla _{X}\nabla _{Y}-\nabla _{Y}\nabla _{X}-\nabla _{[X,Y]}\right)Z=R(X,Y)Z

где – тензор кривизны Римана. $R$

Координатное выражение

Преобразуя в обозначение тензорного индекса , тензор кривизны Римана имеет вид

R^{\rho }{}_{\sigma \mu \nu }=dx^{\rho }\left(R\left(\partial _{\mu },\partial _{\nu }\right)\partial _{\sigma }\right)

где координатные векторные поля. Вышеприведенное выражение можно записать с использованием символов Кристоффеля : $\partial _{\mu }=\partial /\partial x^{\mu }$

R^{\rho }{}_{\sigma \mu \nu }=\partial _{\mu }\Gamma ^{\rho }{}_{\nu \sigma }-\partial _{\nu }\Gamma ^{\rho }{}_{\mu \sigma }+\Gamma ^{\rho }{}_{\mu \lambda }\Gamma ^{\lambda }{}_{\nu \sigma }-\Gamma ^{\rho }{}_{\nu \lambda }\Gamma ^{\lambda }{}_{\mu \sigma }

(см. также список формул римановой геометрии ).

Симметрии и тождества

Тензор кривизны Римана имеет следующие симметрии и тождества:

где скобка относится к скалярному произведению в касательном пространстве, индуцированному метрическим тензором , а скобки и круглые скобки в индексах обозначают операторы антисимметризации и симметризации соответственно. Если кручение ненулевое , тождества Бьянки включают тензор кручения . $\langle ,\rangle$

Первое (алгебраическое) тождество Бьянки было открыто Риччи , но его часто называют первым тождеством Бьянки или алгебраическим тождеством Бьянки , поскольку оно похоже на дифференциальное тождество Бьянки . ^{[ нужна цитата ]}

Первые три тождества образуют полный список симметрий тензора кривизны, т.е. для любого тензора, удовлетворяющего приведенным выше тождествам, можно найти риманово многообразие с таким тензором кривизны в некоторой точке. Простые расчеты показывают, что такой тензор имеет независимые компоненты. ^[9] Из этого следует взаимообменная симметрия. Алгебраические симметрии также эквивалентны утверждению, что R принадлежит образу симметризатора Юнга , соответствующему разбиению 2+2. $n^{2}\left(n^{2}-1\right)/12$

На римановом многообразии имеется ковариантная производная , а тождество Бьянки (часто называемое вторым тождеством Бьянки или дифференциальным тождеством Бьянки) принимает форму последнего тождества в таблице. $\nabla _{u}R$

кривизна Риччи

Тензор кривизны Риччи представляет собой сжатие первого и третьего индексов тензора Римана.

\underbrace {R_{ab}} _{\text{Ricci}}\equiv \underbrace {R^{c}{}_{acb}} _{\text{Riemann}}=g^{cd}\underbrace {R_{cadb}} _{\text{Riemann}}

Особые случаи

Поверхности

Для двумерной поверхности тождества Бьянки означают, что тензор Римана имеет только одну независимую компоненту, а это означает, что скаляр Риччи полностью определяет тензор Римана. Существует только одно допустимое выражение для тензора Римана, которое соответствует требуемым симметриям:

R_{abcd}=f(R)\left(g_{ac}g_{db}-g_{ad}g_{cb}\right)

и дважды сжимая метрику, мы находим явный вид:

R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right),

где — метрический тензор , а — функция, называемая гауссовой кривизной , а a , b , c и d принимают значения либо 1, либо 2. Тензор Римана имеет только один функционально независимый компонент. Гауссова кривизна совпадает с секционной кривизной поверхности. Это также ровно половина скалярной кривизны 2-многообразия, а тензор кривизны Риччи поверхности просто определяется выражением $g_{ab}$ $K=R/2$

R_{ab}=Kg_{ab}.

Космические формы

Риманово многообразие является пространственной формой , если его секционная кривизна равна константе K. Тензор Римана пространственной формы задается формулой

R_{abcd}=K\left(g_{ac}g_{db}-g_{ad}g_{cb}\right).

И наоборот, за исключением размерности 2, если кривизна риманова многообразия имеет эту форму для некоторой функции K , то из тождеств Бьянки следует, что K постоянна и, таким образом, многообразие является (локально) пространственной формой.

Смотрите также

Цитаты

^ Ли 2018, с. 193.
^ Ли 2018, с. 196.
^ Лоусон, Х. Блейн младший; Мишельсон, Мария-Луиза (1989). Спиновая геометрия . Принстон Ю Пресс. п. 154. ИСБН 978-0-691-08542-5.
^ Synge JL, Шильд А. (1949). Тензорное исчисление. первое издание Dover Publications 1978 года. стр. 83, 107. ISBN. 978-0-486-63612-2.
^ ПАМ Дирак (1996). Общая теория относительности . Издательство Принстонского университета . ISBN 978-0-691-01146-2.
^ аб Лавлок, Дэвид; Рунд, Ханно (1989) [1975]. Тензоры, дифференциальные формы и вариационные принципы . Дувр. п. 84 109. ISBN 978-0-486-65840-7.
^ Риччи, Грегорио ; Леви-Чивита, Туллио (март 1900 г.), «Методы дифференцированного абсолютного и leurs приложений», Mathematische Annalen , 54 (1–2): 125–201, doi : 10.1007/BF01454201, S2CID 120009332
^ Сэндберг, Вернон Д. (1978). «Тензорные сферические гармоники на S 2 и S 3 как проблемы собственных значений» (PDF) . Журнал математической физики . 19 (12): 2441–2446. Бибкод : 1978JMP....19.2441S. дои : 10.1063/1.523649.
^ Бергманн ПГ (1976). Введение в теорию относительности. Дувр. стр. 172–174. ISBN 978-0-486-63282-7.