Аргумент незаменимости Куайна–Патнэма [a] — аргумент в философии математики в пользу существования абстрактных математических объектов, таких как числа и множества, позиция, известная как математический платонизм . Он был назван в честь философов Уилларда Куайна и Хилари Патнэма и является одним из важнейших аргументов в философии математики.
Хотя элементы аргумента незаменимости могли возникнуть у таких мыслителей, как Готтлоб Фреге и Курт Гёдель , разработка аргумента Куайном была уникальной, поскольку он ввел в него ряд своих философских позиций, таких как натурализм , конфирмационный холизм и критерий онтологической приверженности . Патнэм дал аргументу Куайна его первую подробную формулировку в своей книге 1971 года «Философия логики» . Однако позже он пришел к несогласию с различными аспектами мышления Куайна и сформулировал свой собственный аргумент незаменимости, основанный на аргументе об отсутствии чудес в философии науки . Стандартная форма аргумента в современной философии приписывается Марку Коливану ; хотя на нее оказали влияние и Куайн, и Патнэм, она во многом отличается от их формулировок. Она представлена в Стэнфордской энциклопедии философии : [2]
Номиналисты , философы, которые отвергают существование абстрактных объектов, выступили против обеих предпосылок этого аргумента. Влиятельный аргумент Хартри Филда утверждает, что математические сущности необязательны для науки. Этот аргумент был поддержан попытками продемонстрировать, что научные и математические теории можно переформулировать, чтобы удалить все ссылки на математические сущности. Другие философы, включая Пенелопу Мэдди , Эллиотта Собера и Джозефа Мелию , утверждали, что нам не нужно верить во все сущности, которые необходимы для науки. Аргументы этих авторов вдохновили на новую объяснительную версию аргумента , которую поддерживают Алан Бейкер и Марк Коливан, которая утверждает, что математика необходима как для конкретных научных объяснений, так и для целых теорий.
В своей статье 1973 года «Математическая истина» Пол Бенасерраф поднял проблему для философии математики . [b] По мнению Бенасеррафа, математические предложения, такие как «два — простое число», подразумевают существование математических объектов . [5] Он подкрепил это утверждение идеей о том, что математика не должна иметь своей собственной особой семантики , или, другими словами, значение математических предложений должно следовать тем же правилам, что и нематематические предложения. Например, согласно этому рассуждению, если предложение «Марс — планета» подразумевает существование планеты Марс, то предложение «два — простое число» также должно подразумевать существование числа два. [6] Но по мнению Бенасеррафа, если бы математические объекты существовали, они были бы непознаваемы. [5] Это происходит потому, что математические объекты, если они существуют, являются абстрактными объектами : объектами, которые не могут вызывать вещи и которые не имеют местоположения в пространстве и времени. [7] Бенацерраф утверждал, основываясь на каузальной теории познания , что было бы невозможно узнать о таких объектах, поскольку они не могут вступить в причинный контакт с нами. [c] [9] Это называется эпистемологической проблемой Бенацеррафа, поскольку она касается эпистемологии математики, то есть того, как мы узнаем, что мы делаем с математикой. [10]
Философия математики делится на два основных течения: платонизм и номинализм . Платонизм утверждает, что существуют абстрактные математические объекты, такие как числа и множества, в то время как номинализм отрицает их существование. [11] Каждое из этих воззрений сталкивается с проблемами, связанными с проблемой, поднятой Бенацеррафом. Поскольку номинализм отвергает существование математических объектов, он не сталкивается с эпистемологической проблемой, но сталкивается с проблемами, касающимися идеи о том, что математика не должна иметь своей собственной особой семантики. Платонизм не сталкивается с проблемами, касающимися семантической половины дилеммы, но ему трудно объяснить, как мы можем иметь какие-либо знания о математических объектах. [12]
Аргумент о незаменимости направлен на преодоление эпистемологической проблемы, выдвинутой против платонизма, путем предоставления обоснования веры в абстрактные математические объекты. [13] Он является частью широкого класса аргументов о незаменимости, наиболее часто применяемых в философии математики, но также включающих аргументы в философии языка и этики . [14] В самом общем смысле аргументы о незаменимости направлены на поддержку своего заключения, основанного на утверждении, что истинность заключения является незаменимой или необходимой для определенной цели. [15] При применении в области онтологии — изучения того, что существует — они иллюстрируют стратегию Куайна для установления существования спорных сущностей, которые не могут быть исследованы напрямую. Согласно этой стратегии, незаменимость этих сущностей для формулирования теории других менее спорных сущностей считается доказательством их существования. [16] В случае философии математики незаменимость математических сущностей для формулирования научных теорий принимается как доказательство существования этих математических сущностей. [17]
Марк Коливан представляет этот аргумент в Стэнфордской энциклопедии философии в следующей форме: [2]
Здесь онтологическая приверженность сущности — это приверженность вере в то, что эта сущность существует. [18] Первая предпосылка основана на двух фундаментальных предположениях: натурализме и конфирмативном холизме . Согласно натурализму, мы должны обратиться к нашим лучшим научным теориям, чтобы определить, что у нас есть наилучшие основания полагать существующим. [19] Куайн резюмировал натурализм как «признание того, что именно в самой науке, а не в какой-то предшествующей философии, реальность должна быть идентифицирована и описана». [20] Конфирмативный холизм — это точка зрения, согласно которой научные теории не могут быть подтверждены изолированно и должны быть подтверждены как целостности. Следовательно, согласно конфирмативному холизму, если мы должны верить в науку, то мы должны верить во всю науку, включая любую математику, которая предполагается нашими лучшими научными теориями. [19] Аргумент в основном нацелен на номиналистов, которые являются научными реалистами , поскольку он пытается обосновать веру в математические сущности способом, аналогичным обоснованию веры в теоретические сущности, такие как электроны или кварки ; Куайн считал, что у таких номиналистов «двойной стандарт» в отношении онтологии. [2]
Аргумент о незаменимости отличается от других аргументов в пользу платонизма, поскольку он приводит доводы только в пользу веры в те части математики, которые необходимы для науки. Он не обязательно оправдывает веру в самые абстрактные части теории множеств, которые Куайн назвал «математическим воссозданием… без онтологических прав». [21] Некоторые философы делают вывод из этого аргумента, что математическое знание является апостериорным , поскольку он подразумевает, что математические истины могут быть установлены только посредством эмпирического подтверждения научных теорий, для которых они необходимы. Это также указывает на то, что математические истины условны , поскольку эмпирически известные истины, как правило, условны. Такая позиция является спорной, поскольку она противоречит традиционному взгляду на математическое знание как на априорное знание необходимых истин . [22]
Хотя исходный аргумент Куайна является аргументом в пользу платонизма, аргументы незаменимости также могут быть построены для аргументации в пользу более слабого утверждения реализма предложений — утверждения, что математическая теория объективно истинна. Это более слабое утверждение, поскольку оно не обязательно подразумевает, что существуют абстрактные математические объекты. [23] [d]
Вторая предпосылка аргумента незаменимости утверждает, что математические объекты являются незаменимыми для наших лучших научных теорий. В этом контексте незаменимость не то же самое, что и неустранимость, потому что любая сущность может быть устранена из теоретической системы при условии внесения соответствующих корректировок в другие части системы. [25] Вместо этого незаменимость означает, что сущность не может быть устранена без снижения привлекательности теории. Привлекательность теории можно оценить с точки зрения теоретических достоинств, таких как объяснительная сила , эмпирическая адекватность и простота . [26] Более того, если сущность является незаменимой для теории, эквивалентная теория может быть сформулирована без нее. [27] Это имеет место, например, если каждое предложение в одной теории является парафразом предложения в другой или если две теории предсказывают одни и те же эмпирические наблюдения. [28]
Согласно Стэнфордской энциклопедии философии , один из самых влиятельных аргументов против аргумента незаменимости исходит от Хартри Филда . [29] Он отвергает утверждение, что математические объекты необходимы для науки; [30] Филд поддержал этот аргумент, переформулировав или «номинировав» научные теории, чтобы они не ссылались на математические объекты. [31] В рамках этого проекта Филд предложил переформулировку ньютоновской физики в терминах отношений между точками пространства-времени. Вместо того, чтобы ссылаться на числовые расстояния, переформулировка Филда использует такие отношения, как «между» и «конгруэнтно», чтобы восстановить теорию, не подразумевая существования чисел. [32] Джон Берджесс и Марк Балагер предприняли шаги для расширения этого проекта номинализации на области современной физики , включая квантовую механику . [33] Такие философы, как Дэвид Маламент и Отавио Буэно, спорят, являются ли такие переформулировки успешными или вообще возможными, особенно в случае квантовой механики. [34]
Альтернативой платонизму Филд считает математический вымысел , согласно которому математические теории ложны, поскольку они ссылаются на абстрактные объекты, которые не существуют. [35] В рамках своего аргумента против аргумента незаменимости Филд попытался объяснить, как возможно использование ложных математических утверждений наукой без того, чтобы научные предсказания стали ложными. [36] Его аргумент основан на идее, что математика консервативна . Математическая теория консервативна, если в сочетании с научной теорией она не подразумевает ничего о физическом мире, чего бы уже не было в научной теории. [37] Это объясняет, как возможно использование математики научными теориями без того, чтобы предсказания науки стали ложными. Кроме того, Филд попытался указать, как именно математика полезна в применении. [29] Филд считает, что математика полезна для науки, поскольку математический язык обеспечивает полезное сокращение для обсуждения сложных физических систем. [33]
Другой подход к отрицанию того, что математические сущности являются незаменимыми для науки, заключается в переформулировании самих математических теорий таким образом, чтобы они не подразумевали существование математических объектов. Чарльз Чихара , Джеффри Хеллман и Патнэм предложили модальные переформулировки математики, которые заменяют все ссылки на математические объекты утверждениями о возможностях. [33]
Натурализм, лежащий в основе аргумента незаменимости, является формой методологического натурализма , которая утверждает первичность научного метода для определения истины. [38] Другими словами, согласно натурализму Куайна, наши лучшие научные теории являются лучшим руководством к тому, что существует. [19] Эта форма натурализма отвергает идею о том, что философия предшествует и в конечном итоге оправдывает веру в науку, вместо этого утверждая, что наука и философия являются непрерывными друг с другом как часть единого, унифицированного исследования мира. [39] Как таковая, эта форма натурализма исключает идею предшествующей философии, которая может опровергнуть онтологические обязательства науки. [40] Это контрастирует с метафизическими формами натурализма , которые исключают существование абстрактных объектов, поскольку они не являются физическими. [41] Пример такого натурализма поддерживает Дэвид Армстронг . Он придерживается принципа, называемого принципом элеатов , который гласит, что существуют только причинные сущности и нет никаких не причинных сущностей. [42] Натурализм Куайна утверждает, что такой принцип не может быть использован для опровержения онтологической приверженности наших лучших научных теорий математическим сущностям, поскольку философские принципы не могут преобладать над наукой. [43]
Я смеюсь при мысли о том, насколько самонадеянно было бы отвергать математику по философским причинам. Как бы вам понравилась работа, в которой вы говорите математикам, что они должны изменить свои пути и отречься от бесчисленных ошибок, теперь, когда философия обнаружила, что классов нет? Можете ли вы сказать им с серьезным лицом, чтобы они следовали философским аргументам, куда бы они ни привели? Если они оспорят ваши полномочия, будете ли вы хвастаться другими великими открытиями философии: что движение невозможно , что Существо, лучше которого нельзя помыслить, нельзя помыслить несуществующим , ... и так далее, и так далее, до тошноты? Только не я!
Дэвид Льюис, Части классов [44]
Куайн считал свой натурализм фундаментальным предположением, но более поздние философы привели аргументы в его поддержку. Наиболее распространенными аргументами в поддержку натурализма Куайна являются аргументы о послужном списке. Это аргументы, которые апеллируют к успешному послужному списку науки по сравнению с философией и другими дисциплинами. [45] Дэвид Льюис, как известно, выдвинул такой аргумент в отрывке из своей книги 1991 года « Части классов» , высмеивая послужной список философии по сравнению с математикой и утверждая, что идея философии, преобладающей над наукой, абсурдна. [46] Критики аргумента о послужном списке утверждают, что он заходит слишком далеко, полностью дискредитируя философские аргументы и методы, и оспаривают идею о том, что философию можно однозначно считать имеющей плохой послужной список. [47]
Натурализм Куайна также критиковался Пенелопой Мэдди за противоречие математической практике. [48] Согласно аргументу незаменимости, математика подчинена естественным наукам в том смысле, что ее легитимность зависит от них. [49] Но Мэдди утверждает, что математики, похоже, не считают, что их практика каким-либо образом ограничена деятельностью естественных наук. Например, аргументы математиков об аксиомах теории множеств Цермело–Френкеля не апеллируют к их приложениям к естественным наукам. Аналогичным образом Чарльз Парсонс утверждал, что математические истины кажутся очевидными таким образом, что это предполагает, что они не зависят от результатов наших лучших теорий. [50]
Конфирмационный холизм — это точка зрения, согласно которой научные теории и гипотезы не могут быть подтверждены изолированно и должны быть подтверждены вместе как часть более крупного кластера теорий. [51] Примером этой идеи, представленной Майклом Резником , является гипотеза о том, что наблюдатель увидит, как нефть и вода разделяются, если их смешать, потому что они не смешиваются. Эта гипотеза не может быть подтверждена изолированно, поскольку она опирается на такие предположения, как отсутствие какого-либо химического вещества, которое будет мешать их разделению, и что глаза наблюдателя функционируют достаточно хорошо, чтобы наблюдать разделение. [52] Поскольку математические теории также предполагаются научными теориями, конфирмационный холизм подразумевает, что эмпирические подтверждения научных теорий также поддерживают эти математические теории. [53]
Согласно контраргументу Мэдди, тезисы натурализма и конфирмативного холизма, составляющие первую предпосылку аргумента незаменимости, находятся в противоречии друг с другом. Мэдди сказала, что натурализм говорит нам, что мы должны уважать методы, используемые учеными, как лучший метод для раскрытия истины, но ученые не действуют так, как будто мы должны верить во все сущности, которые необходимы для науки. [54] Чтобы проиллюстрировать этот момент, Мэдди использует пример атомной теории ; она утверждает, что, несмотря на то, что атом был необходим для лучших теорий ученых к 1860 году, их реальность не была общепризнанной до 1913 года, когда они были подвергнуты прямой экспериментальной проверке. [55] Мэдди и другие, такие как Мэри Ленг , также апеллируют к тому факту, что ученые используют математические идеализации — например, предполагая, что водоемы бесконечно глубоки — без учета того, являются ли они истинными. [56] По словам Мэдди, это указывает на то, что ученые не рассматривают незаменимое использование математики для науки как оправдание веры в математику или математические сущности. В целом, Мэдди сказала, что мы должны встать на сторону натурализма и отвергнуть конфирмационный холизм, то есть нам не нужно верить во все сущности, которые необходимы для науки. [29]
Другой контраргумент Эллиота Собера утверждает, что математические теории не проверяются так же, как научные теории. Собер утверждает, что научные теории конкурируют с альтернативами, чтобы найти теорию с наибольшей эмпирической поддержкой. Но у математической теории нет альтернатив, с которыми она могла бы конкурировать, потому что все научные теории имеют одно и то же математическое ядро. В результате, по мнению Собера, математические теории не разделяют эмпирическую поддержку наших лучших научных теорий, поэтому мы должны отвергнуть конфирмационный холизм. [57]
Поскольку эти контраргументы были выдвинуты, ряд философов, включая Резника, Алана Бейкера , Патрика Дивени, Дэвида Лиггинса , Джейкоба Буша и Андреа Серени, утверждали, что конфирмационный холизм можно исключить из аргумента. [58] Например, Резник предложил прагматичный аргумент незаменимости, сосредоточенный не столько на понятии доказательств, сколько на практической важности математики в проведении научного исследования. [59]
Другой ключевой частью аргумента является концепция онтологического обязательства . Онтологическое обязательство по отношению к сущности — это обязательство верить в то, что эта сущность существует. Его можно разделить на два компонента: обязательства, принимаемые отдельными людьми, и обязательства теорий, в которые они верят. Куайн считал, что мы должны быть привержены тем же сущностям, которым привержены наши лучшие научные теории. [60] Он сформулировал «критерий онтологического обязательства», который направлен на раскрытие обязательств наших лучших теорий путем перевода или «регламентирования» их с обычного языка на логику первого порядка . [61] Куайн считал, что в обычном языке термин «существует» должен нести онтологическое обязательство; сказать «существует» что-то означает, что эта вещь существует. [e] [63] И для Куайна квантификатор существования в логике первого порядка был естественным эквивалентом «существует». Таким образом, при переводе научных теорий в логику первого порядка критерий Куайна принимает онтологические обязательства теории за все объекты, которые регламентированная теория количественно оценивает . [61]
Куайн считал важным переводить наши лучшие научные теории в логику первого порядка, поскольку обычный язык неоднозначен, тогда как логика может сделать обязательства теории более точными. Перевод теорий в логику первого порядка также имеет преимущества по сравнению с переводом их в логики более высокого порядка, такие как логика второго порядка . Хотя логика второго порядка имеет ту же выразительную силу, что и логика первого порядка, ей не хватает некоторых технических преимуществ логики первого порядка, таких как полнота и компактность . Логика второго порядка также допускает квантификацию по свойствам, таким как «краснота», но есть ли у нас онтологическая приверженность свойствам, является спорным. [18] По мнению Куайна, такая квантификация просто неграмматична. [64]
Джоди Аззуни возражал против критерия онтологической приверженности Куайна, говоря, что квантификатор существования в логике первого порядка не всегда несет онтологическое обязательство. [65] По мнению Аззуни, обычный языковой эквивалент квантификации существования «существует» часто используется в предложениях, не подразумевая онтологического обязательства. В частности, Аззуни указывает на использование «существует» при ссылке на вымышленные объекты в таких предложениях, как «существуют вымышленные детективы, которыми восхищаются некоторые настоящие детективы». [66] По мнению Аззуни, для того, чтобы иметь онтологическое обязательство по отношению к сущности, мы должны иметь правильный уровень эпистемического доступа к ней. Это означает, например, что она должна преодолеть некоторые эпистемические трудности, чтобы мы могли постулировать ее. Но по мнению Аззуни, математические сущности — это «простые постулаты», которые может постулировать кто угодно в любое время, «просто записав набор аксиом», поэтому нам не нужно относиться к ним как к реальным. [67]
Более современные представления аргумента не обязательно принимают критерий онтологического обязательства Куайна и могут допускать прямое определение онтологических обязательств из обычного языка. [68] [f]
Одна из проблем с аргументом, поднятым Джозефом Мелией , заключается в том, что он не учитывает роль математики в науке. По словам Мелии, нам нужно верить в математику только в том случае, если она необходима науке в правильном смысле. В частности, она должна быть необходима для научных объяснений. [70] Но, по словам Мелии, математика играет чисто репрезентативную роль в науке, она просто «[делает] больше вещей, которые можно сказать о конкретных объектах». [71] Он утверждает, что по этой причине законно отказываться от приверженности математике, ссылаясь на лингвистический феномен, который он называет «обманом». Это когда человек делает утверждение, а затем позже отказывается от чего-то, подразумеваемого этим утверждением. Примером обмана, используемого для выражения информации в повседневном контексте, является «У всех, кто пришел на семинар, был раздаточный материал. Но тот, кто пришел с опозданием, его не получил». [72] Здесь передается, казалось бы, противоречивая информация, но если отнестись к этому снисходительно, то просто утверждается, что все, кроме человека, который пришел с опозданием, получили раздаточный материал. [72] Аналогично, по словам Мелии, хотя математика необходима для науки, «почти все ученые... отрицают, что существуют такие вещи, как математические объекты», подразумевая, что приверженность математическим объектам ускользает. [73] Для Мелии такое уклонение приемлемо, потому что математика не играет подлинно объяснительной роли в науке. [74]
Вдохновленные как аргументами против конфирмационного холизма [75], так и аргументом Мелии о том, что мы можем приостановить веру в математику, если она не играет подлинно объяснительной роли в науке, [76] Коливан и Бейкер защитили объяснительную версию аргумента незаменимости . [77] [g] Эта версия аргумента пытается устранить опору на конфирмационный холизм, заменив его выводом о лучшем объяснении . Она утверждает, что мы имеем право верить в математические объекты, потому что они появляются в наших лучших научных объяснениях, а не потому, что они наследуют эмпирическую поддержку наших лучших теорий. [80] Она представлена в Интернет-энциклопедии философии в следующей форме: [77]
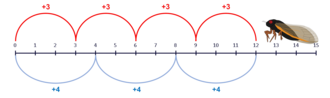
Примером объяснительной незаменимости математики, представленным Бейкером, является периодическая цикада , тип насекомых, жизненный цикл которых обычно составляет 13 или 17 лет. Предполагается, что это эволюционное преимущество, поскольку 13 и 17 являются простыми числами . Поскольку простые числа не имеют нетривиальных множителей, это означает, что хищники вряд ли смогут синхронизироваться с жизненными циклами цикад. Бейкер сказал, что это объяснение, в котором математика, в частности теория чисел , играет ключевую роль в объяснении эмпирического явления. [81]
Другими важными примерами являются объяснения гексагональной структуры пчелиных сот и невозможности пересечь все семь мостов Кёнигсберга только один раз за одну прогулку по городу. [82] Основной ответ на эту форму аргументации, которую приняли такие философы, как Мелия, Крис Дейли, Саймон Лэнгфорд и Юха Саатси, заключается в отрицании того, что существуют подлинно математические объяснения эмпирических явлений, вместо этого определяя роль математики как репрезентативную или индексальную. [83]

Аргумент исторически связан с Уиллардом Куайном и Хилари Патнэмом, но его можно проследить и до более ранних мыслителей, таких как Готтлоб Фреге и Курт Гёдель . В своих аргументах против математического формализма — взгляда, который уподобляет математику игре, подобной шахматам, с правилами о том, как можно манипулировать математическими символами, такими как «2», — Фреге сказал в 1893 году, что «только применимость возводит арифметику из игры в ранг науки». [84] Гёдель в статье 1947 года об аксиомах теории множеств сказал, что если бы новая аксиома имела достаточно проверяемых следствий, ее «пришлось бы принять по крайней мере в том же смысле, что и любую устоявшуюся физическую теорию». [85] Аргументы Фреге и Гёделя отличаются от более позднего аргумента Куайна о незаменимости, поскольку в них отсутствуют такие черты, как натурализм и подчинение практики, что привело некоторых философов, включая Пьеранну Гаравазу , к утверждению, что они не являются подлинными примерами аргумента о незаменимости. [86]
Развивая свой философский взгляд на конфирмационный холизм, Куайн находился под влиянием Пьера Дюгема . [87] В начале двадцатого века Дюгем защищал закон инерции от критиков, которые говорили, что он лишен эмпирического содержания и нефальсифицируем . [52] Эти критики основывали это утверждение на том факте, что закон не делает никаких наблюдаемых предсказаний без постулирования некоторой наблюдаемой системы отсчета и что фальсифицирующих случаев всегда можно избежать, изменив выбор системы отсчета. Дюгем ответил, сказав, что закон производит предсказания, когда сочетается со вспомогательными гипотезами, фиксирующими систему отсчета, и поэтому ничем не отличается от любой другой физической теории. [88] Дюгем сказал, что хотя отдельные гипотезы могут не делать наблюдаемых предсказаний по отдельности, они могут быть подтверждены как части систем гипотез. Куайн распространил эту идею на математические гипотезы, утверждая, что, хотя математические гипотезы сами по себе не имеют эмпирического содержания, они могут участвовать в эмпирических подтверждениях систем гипотез, в которых они содержатся. [89] Этот тезис позже стал известен как тезис Дюгема-Куайна . [90]
Куайн описал свой натурализм как «отказ от цели первой философии. Она рассматривает естественную науку как исследование реальности, подверженное ошибкам и поправимое, но не подлежащее никакому наднаучному суду и не нуждающееся ни в каком обосновании, выходящем за рамки наблюдения и гипотетико -дедуктивного метода ». [91] Термин «первая философия» используется в отношении « Размышлений о первой философии» Декарта , в которых Декарт использовал свой метод сомнения в попытке обеспечить основы науки. Куайн сказал, что попытки Декарта предоставить основы для науки потерпели неудачу и что проект поиска основополагающего обоснования для науки следует отвергнуть, поскольку он считал, что философия никогда не сможет предоставить метод обоснования более убедительный, чем научный метод. [92]
Куайн также находился под влиянием логических позитивистов , таких как его учитель Рудольф Карнап ; его натурализм был сформулирован в ответ на многие из их идей. [93] Для логических позитивистов все обоснованные убеждения сводились к чувственным данным , включая наши знания об обычных объектах, таких как деревья. [94] Куайн критиковал чувственные данные как саморазрушительные, говоря, что мы должны верить в обычные объекты, чтобы организовать наш опыт мира. Он также сказал, что поскольку наука является нашей лучшей теорией того, как чувственный опыт дает нам убеждения об обычных объектах, мы также должны верить в нее. [95] В то время как логические позитивисты говорили, что отдельные утверждения должны подтверждаться чувственными данными, конфирмационный холизм Куайна означает, что научная теория неотъемлемо связана с математической теорией, и поэтому доказательства для научных теорий могут оправдать веру в математические объекты, несмотря на то, что они не воспринимаются напрямую. [94]
Хотя он в конечном итоге стал платоником из-за своей формулировки аргумента незаменимости, [96] Куайн симпатизировал номинализму с ранних этапов своей карьеры. [97] В лекции 1946 года он сказал: «Я выложу свои карты на стол и признаю свои предубеждения: я хотел бы иметь возможность принять номинализм». [98] Он и Нельсон Гудман впоследствии опубликовали совместную статью 1947 года под названием «Шаги к конструктивному номинализму» [99] как часть продолжающегося проекта Куайна по «созданию номиналистического языка, на котором может быть выражена вся естественная наука». [100] Однако в письме Джозефу Генри Вуджеру в следующем году Куайн сказал, что он становится все более убежденным, что «предположение об абстрактных сущностях и предположения о внешнем мире являются предположениями одного и того же рода». [101] Позднее в 1948 году он опубликовал статью «О том, что есть», в которой сказал, что «аналогия между мифом математики и мифом физики... поразительно близка», что ознаменовало переход к его окончательному принятию «вынужденного платонизма». [102]
На протяжении 1950-х годов Куайн регулярно упоминал платонизм, номинализм и конструктивизм как правдоподобные взгляды, и он еще не пришел к окончательному выводу о том, какой из них правильный. [103] Неясно, когда именно Куайн принял платонизм; в 1953 году он дистанцировался от претензий номинализма в своей статье 1947 года с Гудманом, но к 1956 году Гудман все еще описывал «отступничество» Куайна от номинализма как «все еще несколько предварительное». [104] По словам Ливена Декока, Куайн принял необходимость абстрактных математических сущностей, опубликовав свою книгу « Слово и объект» в 1960 году , в которой он написал, что «радикальная номиналистическая доктрина слишком сложна, чтобы ей соответствовать». [105] Однако, хотя он и опубликовал предложения аргумента незаменимости в ряде статей, он никогда не давал его подробной формулировки. [106]
Патнэм впервые явно представил этот аргумент в своей книге 1971 года «Философия логики» , в которой он приписал его Куайну. [107] Он заявил, что аргумент «квантификация математических сущностей необходима для науки, как формальной, так и физической; поэтому мы должны принять такую квантификацию; но это обязывает нас принять существование рассматриваемых математических сущностей». [108] Он также написал, что Куайн «в течение многих лет подчеркивал как незаменимость квантификации математических сущностей, так и интеллектуальную нечестность отрицания существования того, что каждый день предполагает». [108] Поддержка Патнэмом версии аргумента Куайна оспаривается. Интернет-энциклопедия философии утверждает: «В своей ранней работе Хилари Патнэм принял версию аргумента незаменимости Куайна». [109] Лиггинс и Буэно, однако, утверждают, что Патнэм никогда не одобрял этот аргумент и только представлял его как аргумент Куайна. [110] В лекции 1990 года Патнэм сказал, что он разделял взгляды Куайна на аргумент незаменимости с 1948 года, когда он был студентом Гарварда, но с тех пор он пришел к несогласию с ними. [111] Позже он сказал, что он отличался от Куайна в своем отношении к аргументу по крайней мере с 1975 года. [112] Особенности аргумента, с которыми Патнэм пришел к несогласию, включают его опору на единственную, регламентированную, лучшую теорию. [109]
В 1975 году Патнэм сформулировал свой собственный аргумент незаменимости, основанный на аргументе об отсутствии чудес в философии науки, который утверждает, что успех науки может быть объяснен только научным реализмом, не будучи при этом чудом. В том же году он написал: «Я считаю, что позитивный аргумент в пользу реализма [в науке] имеет аналог в случае математического реализма. Здесь я также считаю, что реализм — единственная философия, которая не делает успех науки чудом». [113] Интернет -энциклопедия философии называет эту версию аргумента «аргументом успеха Патнэма» и представляет ее в следующей форме: [109]
Согласно Интернет-энциклопедии философии , первая и вторая предпосылки аргумента были рассмотрены как непротиворечивые, поэтому обсуждение этого аргумента было сосредоточено на третьей предпосылке. Другие позиции, которые пытались объяснить причину успеха математики, включают переформулировки науки Филдом, которые объясняют полезность математики как консервативной стенографии. [109] Патнэм критиковал переформулировки Филда за то, что они применимы только к классической физике и вряд ли могут быть распространены на будущую фундаментальную физику. [116]
По словам Яна Хакинга , не было «согласованного вызова» аргументу незаменимости в течение нескольких десятилетий после того, как Куайн впервые его выдвинул. [117] Чихара в своей книге 1973 года «Онтология и принцип порочного круга» был одним из первых философов, попытавшихся переформулировать математику в ответ на аргументы Куайна. [118] Филд последовал за ним с «Наукой без чисел» в 1980 году и доминировал в дискуссии об аргументе незаменимости на протяжении 1980-х и 1990-х годов. [119] С введением аргументов против первой предпосылки аргумента, первоначально Мэдди в 1990-х годах и продолженных Мелией и другими в 2000-х годах, подход Филда стал известен как «номинализм трудного пути» из-за сложности создания технических реконструкций науки, которые он требует. Подходы, критикующие первую предпосылку, напротив, стали известны как «номинализм легкого пути». [120]
Коливан часто рассматривается как представляющий стандартную или «каноническую» формулировку аргумента в более поздних философских работах. [121] Версия аргумента Коливена оказала влияние на дебаты в современной философии математики. [122] Она отличается в ключевых моментах от аргументов, представленных Куайном и Патнэмом. Версия аргумента Куайна опирается на перевод научных теорий с обычного языка на логику первого порядка для определения ее онтологических обязательств, что явно не требуется Коливэном. Аргументы Патнэма были за объективность математики, но не обязательно за математические объекты. [123] Патнэм явно дистанцировался от этой версии аргумента, заявив, что «с моей точки зрения, описание Коливэном моих аргументов далеко от правильного», и противопоставил свой аргумент незаменимости «фиктивному „аргументу незаменимости Куайна–Патнэма “ ». [124] Коливан сказал, что «приписывание Куайну и Патнэму [является] признанием интеллектуальных долгов, а не указанием на то, что аргумент, в том виде, в котором он представлен, будет одобрен во всех деталях либо Куайном, либо Патнэмом». [125]
Аргумент о незаменимости широко, хотя и не повсеместно, считается лучшим аргументом в пользу платонизма в философии математики. [126] Согласно Стэнфордской энциклопедии философии , некоторые в этой области считают его единственным хорошим аргументом в пользу платонизма. [127] Это один из немногих аргументов, которые стали доминировать в дебатах между математическим реализмом и математическим антиреализмом. [128] В современной философии многие типы номинализма определяют себя как оппозицию аргументу о незаменимости, [129] и он, как правило, рассматривается как самый важный аргумент для преодоления номиналистских взглядов, таких как фикционализм. [130]
Аргументы Куайна и Патнэма также оказали влияние за пределами философии математики, вдохновив аргументы незаменимости в других областях философии. Например, Дэвид Льюис , который был учеником Куайна, использовал аргумент незаменимости, чтобы аргументировать модальный реализм в своей книге 1986 года «О множественности миров» . Согласно его аргументу, квантификация возможных миров необходима для наших лучших философских теорий, поэтому мы должны верить в их конкретное существование. [131] Другие аргументы незаменимости в метафизике защищаются такими философами, как Дэвид Армстронг , Грэм Форбс и Элвин Плантинга , которые утверждали существование положений дел из-за незаменимой теоретической роли, которую они играют в наших лучших философских теориях творцов истины , модальности и возможных миров. [132] В области этики Дэвид Энох расширил критерий онтологического обязательства, используемый в аргументе незаменимости Куайна-Патнэма, чтобы аргументировать моральный реализм . Согласно «аргументу о совещательной незаменимости» Еноха, незаменимость для совещаний так же онтологически обязывает, как и незаменимость для науки, а моральные факты необходимы для совещаний. Поэтому, согласно Еноху, мы должны верить в моральные факты. [133]