основа Грёбнера

Математическая конструкция в компьютерной алгебре

В математике , а точнее в компьютерной алгебре , вычислительной алгебраической геометрии и вычислительной коммутативной алгебре , базис Грёбнера — это особый вид порождающего множества идеала в кольце полиномов K [ x ₁ , ..., x _n ] над полем K . Базис Грёбнера позволяет легко вывести многие важные свойства идеала и связанного с ним алгебраического многообразия , такие как размерность и количество нулей, когда оно конечно. Вычисление базиса Грёбнера — один из основных практических инструментов для решения систем полиномиальных уравнений и вычисления образов алгебраических многообразий при проекциях или рациональных отображениях .

Вычисление базиса Грёбнера можно рассматривать как многомерное нелинейное обобщение как алгоритма Евклида для вычисления наибольших общих делителей полиномов , так и метода исключения Гаусса для линейных систем. ^[1]

Базисы Грёбнера были введены Бруно Бухбергером в его докторской диссертации 1965 года, которая также включала алгоритм для их вычисления ( алгоритм Бухбергера ). Он назвал их в честь своего научного руководителя Вольфганга Грёбнера . В 2007 году Бухбергер получил премию Ассоциации вычислительной техники в Париже Канеллакиса за теорию и практику за эту работу. Однако русский математик Николай Гюнтер ввел похожее понятие в 1913 году, опубликованное в различных российских математических журналах. Эти работы в значительной степени игнорировались математическим сообществом до их повторного открытия в 1987 году Бодо Реншухом и др. ^[2] Аналогичная концепция для многомерных степенных рядов была разработана независимо Хейсуке Хиронакой в ​​1964 году, который назвал их стандартными базисами . Этот термин использовался некоторыми авторами также для обозначения базисов Грёбнера.

Теория базисов Грёбнера была расширена многими авторами в различных направлениях. Она была обобщена на другие структуры, такие как многочлены над кольцами главных идеалов или кольцами многочленов , а также некоторые классы некоммутативных колец и алгебр, такие как алгебры Оре .

Инструменты

Кольцо полиномов

Базисы Грёбнера в первую очередь определяются для идеалов в кольце многочленов над полем K. Хотя теория применима к любому полю, большинство вычислений базиса Грёбнера выполняются либо для поля рациональных чисел , либо для целых чисел по модулю простого числа. ${\displaystyle R=K[x_{1},\ldots ,x_{n}]}$

В контексте базисов Грёбнера ненулевой многочлен в обычно представляется в виде суммы , где — ненулевые элементы K , называемые коэффициентами , а — одночлены (называемые Бухбергером и некоторыми его последователями степенными произведениями ) вида , где — неотрицательные целые числа. Вектор называется вектором-экспонентой одночлена. Когда список переменных фиксирован, запись одночленов часто сокращается до ${\displaystyle R=K[x_{1},\ldots ,x_{n}]}$ ${\displaystyle c_{1}M_{1}+\cdots +c_{m}M_{m},}$ ${\displaystyle c_{i}}$ ${\displaystyle M_{i}}$ ${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}},}$ ${\displaystyle a_{i}}$ ${\displaystyle A=[a_{1},\ldots ,a_{n}]}$ ${\displaystyle X=[x_{1},\ldots ,x_{n}]}$ ${\displaystyle x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}=X^{A}.}$

Мономы однозначно определяются их векторами экспонент, и, когда упорядочение мономов (см. ниже) фиксировано, многочлен однозначно представляется упорядоченным списком упорядоченных пар , образованных вектором экспоненты и соответствующим коэффициентом. Такое представление многочленов особенно эффективно для вычисления базиса Грёбнера на компьютерах, хотя оно менее удобно для других вычислений, таких как факторизация многочленов и наибольший общий делитель многочленов .

Если — конечный набор многочленов в кольце многочленов R , то идеал, порожденный F , — это набор линейных комбинаций элементов F с коэффициентами в R ; это набор многочленов, которые можно записать с помощью ${\displaystyle F=\{f_{1},\ldots ,f_{k}\}}$ ${\textstyle \sum _{i=1}^{k}g_{i}f_{i}}$ ${\displaystyle g_{1},\ldots ,g_{k}\in R.}$

Мономиальное упорядочение

Все операции, связанные с базисами Грёбнера, требуют выбора общего порядка мономов со следующими свойствами совместимости с умножением. Для всех мономов M , N , P ,

1. ${\displaystyle M\leq N\Longleftrightarrow MP\leq NP}$
2. ${\displaystyle M\leq MP}$.

Полный порядок, удовлетворяющий этим условиям, иногда называют допустимым порядком .

Из этих условий следует, что порядок является вполне порядком , то есть каждая строго убывающая последовательность мономов конечна.

Хотя теория базиса Грёбнера не зависит от конкретного выбора допустимого мономиального порядка, три мономиальных порядка особенно важны для приложений:

• Лексикографическое упорядочение , обычно называемое лексом или плексом (для чисто лексического упорядочения).
• Полная степень обратного лексикографического упорядочения , обычно называемая degrevlex .
• Порядок ликвидации , lexdeg .

Теория базиса Грёбнера изначально была введена для лексикографического упорядочения. Вскоре стало понятно, что базис Грёбнера для degrevlex почти всегда гораздо проще вычислить, и что почти всегда проще вычислить базис Грёбнера lex, сначала вычислив базис degrevlex, а затем используя «алгоритм изменения порядка». Когда требуется исключение, degrevlex неудобен; можно использовать и lex, и lexdeg, но, опять же, многие вычисления относительно просты с lexdeg и почти невозможны с lex.

Основные операции

Ведущий член, коэффициент и одночлен

После того, как порядок монома зафиксирован, члены полинома (произведение монома с его ненулевым коэффициентом) естественным образом упорядочиваются по убыванию мономов (для этого порядка). Это делает представление полинома в виде отсортированного списка пар вектор коэффициент–экспонента каноническим представлением полиномов (то есть два полинома равны тогда и только тогда, когда они имеют одинаковое представление).

Первый (наибольший) член многочлена p для этого порядка и соответствующие ему одночлен и коэффициент называются соответственно старшим членом , старшим одночленом и старшим коэффициентом и обозначаются в данной статье как lt( p ), lm( p ) и lc( p ) .

Большинство полиномиальных операций, связанных с базисами Грёбнера, включают ведущие члены. Таким образом, представление полиномов в виде отсортированных списков делает эти операции особенно эффективными (чтение первого элемента списка занимает постоянное время, независимо от длины списка).

Полиномиальные операции

Другие полиномиальные операции, используемые в вычислениях базиса Грёбнера, также совместимы с мономиальным упорядочением; то есть их можно выполнять без переупорядочивания результата:

• Сложение двух многочленов заключается в слиянии двух соответствующих списков членов, со специальной обработкой в ​​случае конфликта (то есть, когда один и тот же одночлен появляется в двух многочленах).
• Умножение многочлена на скаляр состоит в умножении каждого коэффициента на этот скаляр без каких-либо других изменений в представлении.
• Умножение многочлена на одночлен m состоит из умножения каждого одночлена многочлена на m . Это не меняет порядок членов по определению порядка одночленов.

Делимость одночленов

Пусть и будут двумя одночленами с векторами показателей и ${\displaystyle M=x_{1}^{a_{1}}\cdots x_{n}^{a_{n}}}$ ${\displaystyle N=x_{1}^{b_{1}}\cdots x_{n}^{b_{n}}}$ ${\displaystyle A=[a_{1},\ldots ,a_{n}]}$ ${\displaystyle B=[b_{1},\ldots ,b_{n}].}$

Говорят, что M делит N или что N кратно M , если для каждого i ; то есть, если A покомпонентно не больше B. В этом случае частное определяется как Другими словами, вектор показателя степени является покомпонентным вычитанием векторов показателей степени N и M. ${\displaystyle a_{i}\leq b_{i}}$ ${\textstyle {\frac {N}{M}}}$ ${\textstyle {\frac {N}{M}}=x_{1}^{b_{1}-a_{1}}\cdots x_{n}^{b_{n}-a_{n}}.}$ ${\textstyle {\frac {N}{M}}}$

Наибольший общий делитель gcd( M , N ) чисел M и N — это моном , вектор показателя степени которого является покомпонентным минимумом чисел A и B. Наименьшее общее кратное lcm( M , N ) определяется аналогично с max вместо min . ${\textstyle x_{1}^{\min(a_{1},b_{1})}\cdots x_{n}^{\min(a_{n},b_{n})}}$

Один имеет

${\displaystyle \operatorname {lcm} (M,N)={\frac {MN}{\gcd(M,N)}}.}$

Снижение

Редукция полинома другими полиномами относительно мономиального порядка является центральной в теории базиса Грёбнера. Это обобщение как редукции строк , происходящей в гауссовском исключении , так и шагов деления евклидова деления одномерных полиномов . ^{[1] Когда она завершена настолько} , насколько это возможно, ее иногда называют многомерным делением , хотя ее результат не определен однозначно.

Lead-reduction — это особый случай редукции, который проще вычислить. Он имеет основополагающее значение для вычисления базиса Грёбнера, поскольку общая редукция нужна только в конце вычисления базиса Грёбнера, для получения редуцированного базиса Грёбнера из нередуцированного.

Пусть зафиксировано допустимое упорядочение мономов, к которому относится каждое сравнение мономов, которое будет встречаться в этом разделе.

Многочлен f является ведущим приводимым многочленом g , если ведущий моном lm( f ) является кратным lm( g ) . Многочлен f является ведущим приводимым многочленом g , если некоторый моном f является кратным lm( g ) . (Таким образом, если f является ведущим приводимым многочленом g , он также приводим, но f может быть приводимым, не будучи ведущим приводимым.)

Предположим, что f редуцируется с помощью g , и пусть cm — такой член f , что моном m кратен lm( g ) . Одношаговое редуцирование f с помощью g состоит в замене f на

${\displaystyle \operatorname {red} _{1}(f,g)=f-{\frac {c}{\operatorname {lc} (g)}}\,{\frac {m}{\operatorname {lm} (g)}}\,g.}$

Эта операция удаляет моном m из f, не изменяя члены с мономом, большим m (для упорядочения мономов). В частности, одношаговое сокращение свинца f дает многочлен, все мономы которого меньше lm( f ) .

Для данного конечного множества G многочленов говорят, что f является приводимым или приводимо-приводимым к G , если он приводим или приводимо-приводим, соответственно, по крайней мере одним элементом g из G. В этом случае одношаговое сокращение (соответственно одношаговое приводимое сокращение) f к G — это любое одношаговое сокращение (соответственно одношаговое приводимое сокращение) f к элементу G.

(Полное) сокращение (соответственно, сокращение с ведущим) f с помощью G состоит из итераций сокращений за один шаг (соответственно сокращений с ведущим) до тех пор, пока не будет получен полином, который несократим (соответственно, несократим с ведущим) с помощью G. Иногда его называют нормальной формой f с помощью G. В общем случае эта форма не определена однозначно, поскольку, как правило, существует несколько элементов G , которые можно использовать для сокращения f ; эта неоднозначность является отправной точкой теории базиса Грёбнера.

Определение редукции сразу показывает, что если h является нормальной формой f относительно G , то имеем

${\displaystyle f=h+\sum _{g\in G}q_{g}\,g,}$

где h неприводим к G и являются многочленами такими, что В случае одномерных многочленов, если G состоит из одного элемента g , то h является остатком от евклидова деления f на g , а q _g является частным. Более того, алгоритм деления — это в точности процесс свинцовой редукции. По этой причине некоторые авторы используют термин многомерное деление вместо редукции. ${\displaystyle q_{g}}$ ${\displaystyle \operatorname {lm} (q_{g}\,g)\leq \operatorname {lm} (f).}$

Неединственность редукции

В следующем примере есть ровно два полных свинцовых сокращения, которые дают два совершенно разных результата. Тот факт, что результаты неприводимы (а не только свинцовые неприводимые), характерен для этого примера, хотя это довольно распространено для таких небольших примеров.

В этом примере с двумя переменными используется лексикографический порядок с и мы рассматриваем сокращение , на с ${\displaystyle x>y,}$ ${\displaystyle f=2x^{3}-x^{2}y+y^{3}+3y}$ ${\displaystyle G=\{g_{1},g_{2}\},}$ $${\displaystyle {\begin{aligned}g_{1}&=x^{2}+y^{2}-1,\\g_{2}&=xy-2.\end{aligned}}}$$

Для первого шага редукции может быть редуцирован либо первый, либо второй член f . Однако редукцию члена можно свести к удалению этого члена за счет добавления новых нижних членов; если редуцирован не первый редуцированный член, может случиться, что дальнейшее сокращение добавит похожий член, который должен быть редуцирован снова. Поэтому всегда лучше сначала редуктировать наибольший (для порядка монома) редуктируемый член; то есть, в частности, сначала лидировать-редуктировать до получения лидирующего-неприводимого многочлена.

Главный член f сокращается на , а не на . Поэтому первый шаг сокращения состоит в умножении на –2 x и прибавлении результата к f : ${\displaystyle 2x^{3}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2}.}$ ${\displaystyle g_{1}}$

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}=f-2xg_{1}=-x^{2}y-2xy^{2}+2x+y^{3}+3y.}$

Главный член кратен ведущим мономам обоих и Таким образом, у нас есть два выбора для второго шага редукции. Если выбрать, то получим многочлен, который можно снова сократить с помощью ${\displaystyle -x^{2}y}$ ${\displaystyle f_{1}}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2},}$ ${\displaystyle g_{2},}$ ${\displaystyle g_{2}\colon }$

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {xg_{2}} \;-2xy^{2}+y^{3}+3y\;\xrightarrow {2yg_{2}} \;f_{2}=y^{3}-y.}$

Дальнейшее сокращение невозможно, как и полное сокращение f . ${\displaystyle f_{2}}$

При другом выборе на втором этапе получается другой результат:

${\displaystyle f\;\xrightarrow {-2xg_{1}} \;f_{1}\;\xrightarrow {yg_{1}} \;-2xy^{2}+2x+2y^{3}+2y\;\xrightarrow {2yg_{2}} \;f_{3}=2x+2y^{3}-2y.}$

Опять же, результат не поддается уменьшению, хотя было достигнуто только сокращение содержания свинца. ${\displaystyle f_{3}}$

Подводя итог, можно сказать, что полное сокращение f может привести либо к одному , либо к другому ${\displaystyle f_{2}=y^{3}-y}$ ${\displaystyle f_{3}=2x+2y^{3}-2y.}$

Именно для решения проблем, поставленных этой неединственностью, Бухбергер ввел базисы Грёбнера и S -полиномы. Интуитивно, 0 = f − f может быть сведено к Это подразумевает, что принадлежит идеалу, порожденному G . Таким образом, этот идеал не изменяется при добавлении к G , и это допускает больше сокращений. В частности, может быть сведено к на и это восстанавливает единственность приведенной формы. ${\displaystyle f_{2}-f_{3}.}$ ${\displaystyle f_{2}-f_{3}}$ ${\displaystyle f_{3}-f_{2}}$ ${\displaystyle f_{3}}$ ${\displaystyle f_{2}}$ ${\displaystyle f_{3}-f_{2}}$

Здесь алгоритм Бухбергера для базисов Грёбнера начинается с добавления к G многочлена

${\displaystyle g_{3}=yg_{1}-xg_{2}=2x+y^{3}-y.}$

Этот многочлен, названный Бухбергером S -многочленом, представляет собой разность одношаговых сокращений наименьшего общего кратного старших одночленов и на и соответственно: ${\displaystyle x^{2}y}$ ${\displaystyle g_{1}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{1}}$

${\displaystyle g_{3}=\left(x^{2}y-{\frac {x^{2}y}{lt(g_{2})}}g_{2}\right)-\left(x^{2}y-{\frac {x^{2}y}{lt(g_{1})}}g_{1}\right)={\frac {x^{2}y}{lt(g_{1})}}g_{1}-{\frac {x^{2}y}{lt(g_{2})}}g_{2}}$.

В этом примере имеем Это не завершает алгоритм Бухбергера, так как xy дает разные результаты при уменьшении на или ${\displaystyle g_{3}=f_{3}-f_{2}.}$ ${\displaystyle g_{2}}$ ${\displaystyle g_{3}.}$

С-полином

При заданном мономиальном порядке S-полином или критическая пара двух полиномов f и g — это полином

${\displaystyle S(f,g)=\operatorname {red} _{1}(\mathrm {lcm} ,g)-\operatorname {red} _{1}(\mathrm {lcm} ,f)}$;

где lcm обозначает наименьшее общее кратное ведущих мономов f и g . Используя определение , это переводится как: ${\displaystyle \operatorname {red} _{1}}$

${\displaystyle {\begin{aligned}S(f,g)&=\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\right)-\left(\mathrm {lcm} -{\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f\right)\\&={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (f)}}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\mathrm {lcm} }{\operatorname {lm} (g)}}\,g\\\end{aligned}}.}$

Используя свойство, связывающее наименьший кратный и наибольший общий делитель , S -полином можно также записать в виде:

${\displaystyle S(f,g)={\frac {1}{\operatorname {lc} (f)}}\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-{\frac {1}{\operatorname {lc} (g)}}\,{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;}$

где gcd обозначает наибольший общий делитель старших одночленов f и g .

Поскольку мономы, которые редуцируются как f, так и g , являются в точности кратными lcm , можно иметь дело со всеми случаями неоднозначности редукции, рассматривая только S -полиномы. Это фундаментальный факт для теории базиса Грёбнера и всех алгоритмов для их вычисления.

Чтобы избежать дробей при работе с многочленами с целыми коэффициентами, многочлен S часто определяется как

${\displaystyle S(f,g)=\operatorname {lc} (g)\,{\frac {\operatorname {lm} (g)}{\mathrm {gcd} }}\,f-\operatorname {lc} (f)\,{\frac {\operatorname {lm} (f)}{\mathrm {gcd} }}\,g;}$

Это ничего не меняет в теории, поскольку два полинома являются ассоциированными .

Определение

Пусть — кольцо многочленов над полем F. В этом разделе мы предполагаем, что допустимое мономиальное упорядочение зафиксировано. ${\displaystyle R=F[x_{1},\ldots ,x_{n}]}$

Пусть G — конечный набор многочленов в R , который порождает идеал I. Набор G является базисом Грёбнера (относительно мономиального порядка) или, точнее, базисом Грёбнера I , если

1. идеал, порожденный старшими мономами многочленов из I, равен идеалу, порожденному старшими мономами G ,

или, что то же самое,

2. старший моном каждого многочлена из I кратен старшему моному некоторого многочлена из G .

Существует множество характеризующих свойств, каждое из которых может быть принято как эквивалентное определение баз Грёбнера. Для краткости в следующем списке обозначение "одно слово/другое слово" означает, что можно принять либо "одно слово", либо "другое слово" за две различные характеристики баз Грёбнера. Все следующие утверждения являются характеристиками баз Грёбнера:

3. многочлен f принадлежит I тогда и только тогда, когда некоторое/каждое полное сокращение/редукция f с помощью G дает нулевой многочлен;
4. для каждого S -полинома s элементов G некоторое/каждое полное сокращение s с помощью G дает ноль;
5. все полные редукции элемента R дают один и тот же результат;
6. мономы, неприводимые к G, образуют базис векторного пространства F ${\displaystyle R/I.}$

Подсчитав вышеприведенное определение, это дает 12 характеристик базисов Грёбнера. Тот факт, что возможно так много характеристик, делает базисы Грёбнера очень полезными. Например, условие 3 предоставляет алгоритм для проверки идеального членства ; условие 4 предоставляет алгоритм для проверки того, является ли набор полиномов базисом Грёбнера, и формирует основу алгоритма Бухбергера для вычисления базисов Грёбнера; условия 5 и 6 позволяют выполнять вычисления способом, очень похожим на модульную арифметику . ${\displaystyle R/I}$

Существование

Для каждого допустимого мономиального порядка и каждого конечного множества G полиномов существует базис Грёбнера, содержащий G и порождающий тот же идеал. Более того, такой базис Грёбнера может быть вычислен с помощью алгоритма Бухбергера .

Этот алгоритм использует условие 4 и действует примерно следующим образом: для любых двух элементов G вычисляется полное сокращение их S -полинома с помощью G и результат добавляется к G , если он не равен нулю; повторяйте эту операцию с новыми включенными элементами G , пока в конечном итоге все сокращения не дадут ноль.

Алгоритм всегда завершается из-за леммы Диксона или из-за того, что полиномиальные кольца являются нётеровыми ( теорема Гильберта о базисе ). Условие 4 гарантирует, что результат будет базисом Грёбнера, а определения S -полиномов и редукции гарантируют, что сгенерированный идеал не изменится.

Вышеуказанный метод является алгоритмом для вычисления базисов Грёбнера; однако он очень неэффективен. Было предложено и реализовано множество улучшений исходного алгоритма Бухбергера и нескольких других алгоритмов, которые значительно повышают эффективность. См. § Алгоритмы и реализации ниже.

Редуцированные основания Грёбнера

Базис Грёбнера — этоминимальным, если все ведущие мономы его элементов неприводимы к другим элементам базиса. Если задан базис Грёбнера идеалаI, то можно получить минимальный базис ГрёбнераI, удалив многочлены, ведущие мономы которых кратны ведущему моному другого элемента базиса Грёбнера. Однако, если два многочлена базиса имеют одинаковый ведущий моном, то нужно удалить только один. Таким образом, каждый базис Грёбнера содержит минимальный базис Грёбнера как подмножество.

Все минимальные базисы Грёбнера заданного идеала (для фиксированного порядка мономов) имеют одинаковое количество элементов и одинаковые старшие мономы, а неминимальные базисы Грёбнера имеют больше элементов, чем минимальные.

Базис Грёбнера — этосокращенным, если каждый полином в нем несократим другими элементами базиса и имеет1в качестве старшего коэффициента. Таким образом, каждый сокращенный базис Грёбнера является минимальным, но минимальный базис Грёбнера не обязательно должен быть сокращенным.

Если задан базис Грёбнера идеала I , то можно получить редуцированный базис Грёбнера I , сначала удалив полиномы, которые можно сократить с помощью других элементов базиса (для получения минимального базиса); затем заменив каждый элемент базиса результатом полной редукции с помощью других элементов базиса; и, наконец, разделив каждый элемент базиса на его старший коэффициент.

Все приведенные базисы Грёбнера идеала (для фиксированного мономиального порядка) равны. Отсюда следует, что два идеала равны тогда и только тогда, когда они имеют один и тот же приведенный базис Грёбнера.

Иногда редуцированные базисы Грёбнера определяются без условия на старшие коэффициенты. В этом случае уникальность редуцированных базисов Грёбнера верна только с точностью до умножения многочленов на ненулевую константу.

При работе с многочленами над полем рациональных чисел полезно работать только с многочленами с целыми коэффициентами. В этом случае условие на старшие коэффициенты в определении приведенного базиса можно заменить условием, что все элементы базиса являются примитивными многочленами с целыми коэффициентами, причем старшие коэффициенты положительные. Это восстанавливает единственность приведенных базисов. ${\displaystyle \mathbb {Q} }$

Особые случаи

Для каждого мономиального порядка пустой набор многочленов является единственным базисом Грёбнера нулевого идеала .

Для каждого мономиального порядка множество многочленов, содержащее ненулевую константу, является базисом Грёбнера единичного идеала (всего кольца многочленов). Наоборот, каждый базис Грёбнера единичного идеала содержит ненулевую константу. Приведенный базис Грёбнера единичного идеала образован единственным многочленом 1 .

В случае полиномов от одной переменной существует единственно допустимое мономиальное упорядочение — упорядочение по степени. Минимальные базисы Грёбнера — это синглтоны, состоящие из одного полинома. Редуцированные базисы Грёбнера — это мономиальные полиномы .

Пример и контрпример

Нули образуют красную параболу; нули образуют три синие вертикальные линии. Их пересечение состоит из трех точек. ${\displaystyle f}$ ${\displaystyle g}$

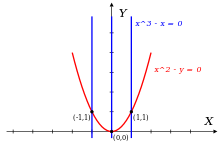
Пусть — кольцо двумерных многочленов с рациональными коэффициентами, и рассмотрим идеал, порожденный многочленами ${\displaystyle R=\mathbb {Q} [x,y]}$ ${\displaystyle I=\langle f,g\rangle }$

${\displaystyle f=x^{2}-y}$,

${\displaystyle g=x^{3}-x}$.

Уменьшая g на f , получаем новый многочлен k, такой что ${\displaystyle I=\langle f,k\rangle :}$

${\displaystyle k=g-xf=xy-x.}$

Ни один из f и k не может быть сведен другим, но xk может быть сведен к f , что дает другой многочлен от I :

${\displaystyle h=xk-(y-1)f=y^{2}-y.}$

При лексикографическом упорядочении с мы имеем ${\displaystyle x>y}$

lt( f ) = x ²

lt( k ) = ху

^lt ( h ) = y2

Так как f , k и h принадлежат I , и ни один из них не редуцируется другими, ни один из и не является базисом Грёбнера I. ${\displaystyle \{f,k\},}$ ${\displaystyle \{f,h\},}$ ${\displaystyle \{h,k\}}$

С другой стороны, { f , k , h } является базисом Грёбнера для I , поскольку S-полиномы

${\displaystyle {\begin{aligned}yf-xk&=y(x^{2}-y)-x(xy-x)=f-h\\yk-xh&=y(xy-x)-x(y^{2}-y)=0\\y^{2}f-x^{2}h&=y(yf-xk)+x(yk-xh)\end{aligned}}}$

может быть сведено к нулю с помощью f , k и h .

Метод, который был использован здесь для нахождения h и k и доказательства того, что { f , k , h } является базисом Грёбнера, является прямым применением алгоритма Бухбергера . Таким образом, его можно механически применить к любому подобному примеру, хотя, в общем случае, необходимо рассмотреть много полиномов и S-полиномов, а вычисление, как правило, слишком велико для выполнения без компьютера.

Свойства и применение оснований Грёбнера

Если явно не указано иное, все последующие результаты ^[3] верны для любого мономиального порядка (см. эту статью для определений различных порядков, которые упоминаются ниже).

Распространенное заблуждение, что для некоторых из этих результатов необходим лексикографический порядок. Напротив, лексикографический порядок почти всегда является самым сложным для вычисления, и его использование делает непрактичными многие вычисления, которые относительно просты с градуированным обратным лексикографическим порядком (grevlex) или, когда требуется исключение, порядком исключения (lexdeg), который ограничивается grevlex для каждого блока переменных.

Равенство идеалов

Редуцированные базисы Грёбнера уникальны для любого заданного идеала и любого мономиального порядка. Таким образом, два идеала равны тогда и только тогда, когда они имеют один и тот же (редуцированный) базис Грёбнера (обычно программное обеспечение для создания базиса Грёбнера всегда создает редуцированные базисы Грёбнера).

Членство и включение идеалов

Редукция многочлена f по базису Грёбнера G идеала I дает 0 тогда и только тогда, когда f принадлежит I . Это позволяет проверить принадлежность элемента идеалу. Другой метод состоит в проверке того, что базис Грёбнера G ∪{ f } равен G .

Чтобы проверить, содержится ли идеал I, порожденный f ₁ , ..., f _{k ,} в идеале J , достаточно проверить, что каждый f _I принадлежит J . Можно также проверить равенство приведенных базисов Грёбнера J и J ∪ { f ₁ , ..., f _k } .

Решения системы алгебраических уравнений

Любой набор полиномов можно рассматривать как систему полиномиальных уравнений , приравнивая полиномы нулю. Набор решений такой системы зависит только от порожденного идеала и, следовательно, не меняется при замене данного порождающего набора на базис Грёбнера, для любого упорядочения, порожденного идеала. Такое решение с координатами в алгебраически замкнутом поле, содержащем коэффициенты полиномов, называется нулем идеала . В обычном случае рациональных коэффициентов это алгебраически замкнутое поле выбирается в качестве комплексного поля .

Идеал не имеет нулей (система уравнений противоречива ) тогда и только тогда, когда 1 принадлежит идеалу (это Nullstellensatz Гильберта ), или, что эквивалентно, если его базис Грёбнера (для любого мономиального порядка) содержит 1, или, также, если соответствующий редуцированный базис Грёбнера равен [1].

Если задан базис Грёбнера G идеала I , он имеет только конечное число нулей, тогда и только тогда, когда для каждой переменной x G содержит многочлен со старшим мономом, который является степенью x (без какой-либо другой переменной, появляющейся в старшем члене). Если это так, то число нулей, подсчитанное с кратностью, равно числу мономов, которые не кратны ни одному старшему моному G. Это число называется степенью идеала.

Когда число нулей конечно, базис Грёбнера для лексикографического мономиального упорядочения теоретически обеспечивает решение: первая координата решения является корнем наибольшего общего делителя многочленов базиса, зависящих только от первой переменной. После подстановки этого корня в базис вторая координата этого решения является корнем наибольшего общего делителя полученных многочленов, зависящих только от второй переменной, и так далее. Этот процесс решения является только теоретическим, поскольку подразумевает вычисление НОД и нахождение корней многочленов с приближенными коэффициентами, что нецелесообразно из-за числовой нестабильности. Поэтому были разработаны другие методы решения полиномиальных систем с помощью базисов Грёбнера (см. Система полиномиальных уравнений для более подробной информации).

Размерность, степень и ряд Гильберта

Размерность идеала I в кольце многочленов R — это размерность Крулля кольца R / I , равная размерности алгебраического множества нулей I. Она также равна числу гиперплоскостей в общем положении , необходимых для пересечения с алгебраическим множеством, которое является конечным числом точек. Степень идеала и связанного с ним алгебраического множества — это число точек этого конечного пересечения, подсчитанное с кратностью. В частности, степень гиперповерхности равна степени ее определяющего многочлена.

Как степень, так и размерность зависят только от набора старших мономов базиса Грёбнера идеала для любого мономиального упорядочения.

Размерность — это максимальный размер подмножества S переменных, такой, что не существует ведущего монома, зависящего только от переменных из S. Таким образом, если идеал имеет размерность 0, то для каждой переменной x существует ведущий моном в базисе Грёбнера, который является степенью x .

И размерность, и степень могут быть выведены из ряда Гильберта идеала, который является рядом , где — число мономов степени i , которые не кратны ни одному ведущему моному в базисе Грёбнера. Ряд Гильберта может быть просуммирован в рациональную дробь ${\textstyle \sum _{i=0}^{\infty }d_{i}t^{i}}$ ${\displaystyle d_{i}}$

${\displaystyle \sum _{i=0}^{\infty }d_{i}t^{i}={\frac {P(t)}{(1-t)^{d}}},}$

где d — размерность идеала, а — многочлен такой, что — степень идеала. ${\displaystyle P(t)}$ ${\displaystyle P(1)}$

Хотя размерность и степень не зависят от выбора порядка мономов, ряд Гильберта и многочлен изменяются при изменении порядка мономов. ${\displaystyle P(t)}$

Большинство систем компьютерной алгебры , предоставляющих функции для вычисления базисов Грёбнера, предоставляют также функции для вычисления рядов Гильберта, а значит, и размерности и степени.

Устранение

Вычисление базисов Грёбнера для элиминационного мономиального упорядочения допускает вычислительную теорию элиминации . Она основана на следующей теореме.

Рассмотрим полиномиальное кольцо , в котором переменные разделены на два подмножества X и Y . Давайте также выберем элиминационное мономиальное упорядочение, «элиминирующее» X , то есть мономиальное упорядочение, для которого два монома сравниваются путем сравнения сначала X -частей, и, в случае равенства, рассмотрения только Y -частей. Это означает, что моном, содержащий X -переменную, больше любого монома, независимого от X . Если G является базисом Грёбнера идеала I для этого мономиального упорядочения, то является базисом Грёбнера (этот идеал часто называют идеалом элиминации ). Более того, состоит в точности из полиномов G , чьи главные члены принадлежат K [ Y ] (это очень упрощает вычисление , так как нужно проверять только главные мономы). ${\displaystyle K[x_{1},\ldots ,x_{n},y_{1},\ldots ,y_{m}]=K[X,Y],}$ ${\displaystyle G\cap K[Y]}$ ${\displaystyle I\cap K[Y]}$ ${\displaystyle G\cap K[Y]}$ ${\displaystyle G\cap K[Y]}$

Это свойство исключения имеет множество применений, некоторые из которых описаны в следующих разделах.

Другое применение в алгебраической геометрии состоит в том, что исключение реализует геометрическую операцию проекции аффинного алгебраического множества в подпространство объемлющего пространства: с указанными выше обозначениями ( замыкание Зарисского ) проекции алгебраического множества, определяемого идеалом I, в подпространство Y определяется идеалом ${\displaystyle I\cap K[Y].}$

Лексикографическое упорядочение, такое что является элиминационным упорядочением для каждого разбиения Таким образом, базис Грёбнера для этого упорядочения несет гораздо больше информации, чем обычно необходимо. Это может объяснить, почему базисы Грёбнера для лексикографического упорядочения обычно являются самыми сложными для вычисления. ${\displaystyle x_{1}>\cdots >x_{n}}$ ${\displaystyle \{x_{1},\ldots ,x_{k}\},\{x_{k+1},\ldots ,x_{n}\}.}$

Пересекающиеся идеалы

Если I и J — два идеала, порожденные соответственно { f ₁ , ..., f _m } и { g ₁ , ..., g _k }, то вычисление одного базиса Грёбнера создает базис Грёбнера их пересечения I ∩ J . Для этого вводится новый неопределенный t , и используется порядок исключения, такой что первый блок содержит только t , а другой блок содержит все остальные переменные (это означает, что моном, содержащий t , больше любого монома, который не содержит t ). С этим порядком мономов базис Грёбнера I ∩ J состоит из многочленов, которые не содержат t , в базисе Грёбнера идеала

${\displaystyle K=\langle tf_{1},\ldots ,tf_{m},(1-t)g_{1},\ldots ,(1-t)g_{k}\rangle .}$

Другими словами, I ∩ J получается путем исключения t из K. Это можно доказать, заметив, что идеал K состоит из многочленов, таких что и . Такой многочлен независим от t тогда и только тогда, когда a = b , что означает, что ${\displaystyle (a-b)t+b}$ ${\displaystyle a\in I}$ ${\displaystyle b\in J}$ ${\displaystyle b\in I\cap J.}$

Имплицитация рациональной кривой

Рациональная кривая — это алгебраическая кривая , имеющая набор параметрических уравнений вида

${\displaystyle {\begin{aligned}x_{1}&={\frac {f_{1}(t)}{g_{1}(t)}}\\&\;\;\vdots \\x_{n}&={\frac {f_{n}(t)}{g_{n}(t)}},\end{aligned}}}$

где и являются одномерными многочленами для 1 ≤ i ≤ n . Можно (и будем) предполагать, что и являются взаимно простыми (они не имеют непостоянных общих множителей). ${\displaystyle f_{i}(t)}$ ${\displaystyle g_{i}(t)}$ ${\displaystyle f_{i}(t)}$ ${\displaystyle g_{i}(t)}$

Имплицитация заключается в вычислении неявных уравнений такой кривой. В случае n = 2, то есть для плоских кривых, это может быть вычислено с результирующим . Неявное уравнение представляет собой следующий результирующий:

${\displaystyle {\text{Res}}_{t}(g_{1}x_{1}-f_{1},g_{2}x_{2}-f_{2}).}$

Исключение с базисами Грёбнера позволяет имплицитно определить для любого значения n , просто исключив t в идеале Если n = 2, результат тот же, что и с результирующим, если отображение инъективно для почти каждого t . В другом случае результирующий является степенью результата исключения. ${\displaystyle \langle g_{1}x_{1}-f_{1},\ldots ,g_{n}x_{n}-f_{n}\rangle .}$ ${\displaystyle t\mapsto (x_{1},x_{2})}$

Насыщенность

При моделировании задачи с помощью полиномиальных уравнений часто предполагается, что некоторые величины не равны нулю, чтобы избежать вырожденных случаев. Например, при работе с треугольниками многие свойства становятся ложными, если треугольник вырождается в отрезок прямой, т. е. длина одной стороны равна сумме длин других сторон. В таких ситуациях нельзя вывести соответствующую информацию из полиномиальной системы, если не игнорировать вырожденные решения. Точнее, система уравнений определяет алгебраическое множество , которое может иметь несколько неприводимых компонентов , и необходимо удалить компоненты, на которых условия вырождения везде равны нулю.

Это делается путем насыщения уравнений условиями вырождения, что может быть сделано с помощью свойства исключения базисов Грёбнера.

Определение насыщенности

Локализация кольца заключается в присоединении к нему формальных обратных некоторых элементов. В этом разделе рассматривается только случай одного элемента или, что эквивалентно, конечного числа элементов (присоединение обратных элементов нескольких элементов эквивалентно присоединению обратного их произведения). Локализация кольца R элементом f — это кольцо , где t — новая неопределенность, представляющая обратный элемент к f . Локализация идеала I кольца R — это идеал Когда R — многочленное кольцо, вычисления в неэффективны из-за необходимости управления знаменателями. Поэтому локализация обычно заменяется операцией насыщения . ${\displaystyle R_{f}=R[t]/(1-ft),}$ ${\displaystyle R_{f}I}$ ${\displaystyle I_{f}.}$ ${\displaystyle R_{f}}$

Theнасыщенность относительноfидеалаIвRесть обратный образпри каноническом отображении изRвЭто идеал,состоящий из всех элементовR, произведение которых с некоторой степеньюfпринадлежитI. ${\displaystyle R_{f}I}$ ${\displaystyle R_{f}.}$ ${\displaystyle I:f^{\infty }=\{g\in R\mid (\exists k\in \mathbb {N} )f^{k}g\in I\}}$

Если J — идеал, порожденный I и 1− ft в R [ t ], то отсюда следует, что если R — кольцо многочленов, то вычисление базиса Грёбнера, исключающее t, дает базис Грёбнера насыщения идеала многочленом. ${\displaystyle I:f^{\infty }=J\cap R.}$

Важное свойство насыщения, гарантирующее, что оно удаляет из алгебраического множества, определяемого идеалом I, неприводимые компоненты, на которых многочлен f равен нулю, заключается в следующем: первичное разложение состоит из компонентов первичного разложения I, которые не содержат никакой степени f . ${\displaystyle I:f^{\infty }}$

Расчет насыщенности

Базис Грёбнера насыщения посредством f полиномиального идеала, порожденного конечным набором полиномов F , может быть получен путем исключения t из , то есть путем сохранения полиномов независимыми от t в базисе Грёбнера для порядка исключения, исключающего t . ${\displaystyle F\cup \{1-tf\},}$ ${\displaystyle F\cup \{1-tf\}}$

Вместо использования F можно также начать с базиса Грёбнера F . Какой метод наиболее эффективен, зависит от задачи. Однако, если насыщение не удаляет ни одного компонента, то есть если идеал равен своему насыщенному идеалу, вычисление сначала базиса Грёбнера F обычно происходит быстрее. С другой стороны, если насыщение удаляет некоторые компоненты, прямое вычисление может быть значительно быстрее.

Если требуется выполнить насыщение относительно нескольких полиномов или относительно одного полинома, который является произведением, есть три способа, которые дают одинаковый результат, но могут иметь совершенно разное время вычислений (это зависит от задачи, которая является наиболее эффективной). ${\displaystyle f_{1},\ldots ,f_{k}}$ ${\displaystyle f=f_{1}\cdots f_{k},}$

• Насыщение в одном вычислении базиса Грёбнера. ${\displaystyle f=f_{1}\cdots f_{k}}$
• Насыщаем, затем насыщаем результат и так далее. ${\displaystyle f_{1},}$ ${\displaystyle f_{2},}$
• Добавление к F или к его базису Грёбнера полиномов и исключение в одном вычислении базиса Грёбнера. ${\displaystyle 1-t_{1}f_{1},\ldots ,1-t_{k}f_{k},}$ ${\displaystyle t_{i}}$

Эффективный Nullstellensatz

Nullstellensatz Гильберта имеет две версии. Первая утверждает, что множество многочленов не имеет общих нулей над алгебраическим замыканием поля коэффициентов, если и только если 1 принадлежит сгенерированному идеалу. Это легко проверить с помощью вычисления базиса Грёбнера, поскольку 1 принадлежит идеалу тогда и только тогда, когда 1 принадлежит базису Грёбнера идеала, для любого мономиального порядка.

Вторая версия утверждает, что множество общих нулей (в алгебраическом замыкании поля коэффициентов) идеала содержится в гиперповерхности нулей многочлена f , тогда и только тогда, когда степень f принадлежит идеалу. Это можно проверить, насытив идеал f ; на самом деле, степень f принадлежит идеалу тогда и только тогда, когда насыщение f дает базис Грёбнера, содержащий 1.

Имплицитация в более высоком измерении

По определению, аффинное рациональное многообразие размерности k может быть описано параметрическими уравнениями вида

${\displaystyle {\begin{aligned}x_{1}&={\frac {p_{1}}{p_{0}}}\\&\;\;\vdots \\x_{n}&={\frac {p_{n}}{p_{0}}},\end{aligned}}}$

где — n +1 многочлен от k переменных (параметры параметризации). Таким образом, параметры и координаты точек многообразия являются нулями идеала ${\displaystyle p_{0},\ldots ,p_{n}}$ ${\displaystyle t_{1},\ldots ,t_{k}.}$ ${\displaystyle t_{1},\ldots ,t_{k}}$ ${\displaystyle x_{1},\ldots ,x_{n}}$

${\displaystyle I=\left\langle p_{0}x_{1}-p_{1},\ldots ,p_{0}x_{n}-p_{n}\right\rangle .}$

Можно было бы предположить, что достаточно исключить параметры, чтобы получить неявные уравнения многообразия, как это было сделано в случае кривых. К сожалению, это не всегда так. Если имеют общий нуль (иногда называемый базовой точкой ), каждый неприводимый компонент непустого алгебраического множества, определяемого , является неприводимым компонентом алгебраического множества, определяемого I . Из этого следует, что в этом случае прямое исключение дает пустой набор многочленов. ${\displaystyle p_{i}}$ ${\displaystyle p_{i}}$ ${\displaystyle t_{i}}$

Следовательно, если k > 1, для вычисления необходимо выполнить два базиса Грёбнера:

1. Насыщаем , чтобы получить основу Грёбнера ${\displaystyle I}$ ${\displaystyle p_{0}}$ ${\displaystyle G}$
2. Исключим из , чтобы получить базис Грёбнера идеала (неявных уравнений) многообразия. ${\displaystyle t_{i}}$ ${\displaystyle G}$

Алгоритмы и реализации

Алгоритм Бухбергера — старейший алгоритм вычисления базисов Грёбнера. Он был разработан Бруно Бухбергером вместе с теорией базисов Грёбнера. Он прост в реализации, но вскоре выяснилось, что сырые реализации могут решать только тривиальные задачи. Основные проблемы следующие:

1. Даже когда результирующий базис Грёбнера мал, промежуточные полиномы могут быть огромными. Это приводит к тому, что большая часть вычислительного времени может быть потрачена на управление памятью . Таким образом, специализированные алгоритмы управления памятью могут быть фундаментальной частью эффективной реализации.
2. Целые числа, возникающие во время вычислений, могут быть достаточно большими для того, чтобы сделать полезными быстрые алгоритмы умножения и многомодулярную арифметику . По этой причине большинство оптимизированных реализаций используют GMPlibrary . Также в оптимизированных реализациях используются модульная арифметика , китайская теорема об остатках и подъем Гензеля
3. Выбор S-полиномов для редукции и полиномов, используемых для их редукции, посвящен эвристике . Как и во многих вычислительных задачах, эвристика не может обнаружить большинство скрытых упрощений, и если избегать эвристического выбора, можно получить резкое улучшение эффективности алгоритма.
4. В большинстве случаев большинство вычисляемых S-полиномов сводятся к нулю; то есть большая часть вычислительного времени тратится на вычисление нуля.
5. Мономиальное упорядочение , которое чаще всего требуется для приложений (чисто лексикографическое), не является упорядочением, приводящим к самым простым вычислениям, как правило, это упорядочение degrevlex .

Для решения 3. было предложено много улучшений, вариантов и эвристик до введения алгоритмов F4 и F5 Жаном -Шарлем Фожером . Поскольку эти алгоритмы разработаны для целочисленных коэффициентов или с коэффициентами в целых числах по модулю простого числа , алгоритм Бухбергера остается полезным для более общих коэффициентов.

Грубо говоря, алгоритм F4 решает 3., заменяя множество S-полиномиальных редукций на редукцию строк одной большой матрицы, для которой можно использовать продвинутые методы линейной алгебры . Это частично решает проблему 4., поскольку редукции к нулю в алгоритме Бухбергера соответствуют соотношениям между строками матрицы, подлежащей редукции, а нулевые строки редуцированной матрицы соответствуют базису векторного пространства этих соотношений.

Алгоритм F5 улучшает F4, вводя критерий, который позволяет уменьшить размер матриц, которые должны быть сокращены. Этот критерий почти оптимален, поскольку матрицы, которые должны быть сокращены, имеют полный ранг в достаточно регулярных случаях (в частности, когда входные полиномы образуют регулярную последовательность ). Настройка F5 для общего использования сложна, поскольку его производительность зависит от порядка входных полиномов и баланса между приращением степени рабочего полинома и количеством рассматриваемых входных полиномов. На сегодняшний день (2022 г.) не существует распределенной реализации, которая была бы значительно эффективнее F4, но над модульными целыми числами F5 успешно использовался для нескольких криптографических задач ; например, для взлома задачи HFE .

Проблема 5. была решена путем открытия алгоритмов преобразования базиса, которые начинаются с базиса Грёбнера для одного мономиального порядка для вычисления базиса Грёбнера для другого мономиального порядка. Алгоритм FGLM — это такой алгоритм преобразования базиса, который работает только в нульмерном случае (где многочлены имеют конечное число комплексных общих нулей) и имеет полиномиальную сложность по числу общих нулей. Алгоритм преобразования базиса, который работает в общем случае, — это алгоритм обхода Грёбнера . ^[4] В своей первоначальной форме FGLM может быть критическим шагом для решения систем полиномиальных уравнений , поскольку FGML не учитывает разреженность вовлеченных матриц . Это было исправлено путем введения разреженных алгоритмов FGLM . ^[5]

Большинство систем компьютерной алгебры общего назначения имеют реализации одного или нескольких алгоритмов для базисов Грёбнера, часто также встроенных в другие функции, такие как решение систем полиномиальных уравнений или упрощение тригонометрических функций; это касается, например, CoCoA , GAP , Macaulay 2 , Magma , Maple , Mathematica , SINGULAR , SageMath и SymPy . Когда доступен F4, он, как правило, намного эффективнее алгоритма Бухбергера. Методы реализации и алгоритмические варианты не всегда документируются, хотя они могут оказывать существенное влияние на эффективность.

Реализации F4 и (разреженного)-FGLM включены в библиотеку Msolve . ^[6] Помимо алгоритмов Грёбнера, Msolve содержит быстрые алгоритмы для изоляции действительных корней и объединяет все эти функции в алгоритм для действительных решений систем полиномиальных уравнений , который значительно превосходит другое программное обеспечение для этой задачи (Maple и Magma). ^[6] Msolve доступен на GitHub и взаимодействует с Julia , Maple и SageMath; это означает, что Msolve можно использовать непосредственно из этих программных сред.

Сложность

Сложность вычислений базиса Грёбнера обычно оценивается с точки зрения числа n переменных и максимальной степени d входных полиномов.

В худшем случае основным параметром сложности является максимальная степень элементов полученного редуцированного базиса Грёбнера. Точнее, если базис Грёбнера содержит элемент большой степени D , этот элемент может содержать ненулевые члены, вычисление которых требует времени С другой стороны, если все многочлены в редуцированном базисе Грёбнера однородного идеала имеют степень не более D , базис Грёбнера может быть вычислен с помощью линейной алгебры на векторном пространстве многочленов степени меньше 2 D , которое имеет размерность ^[1] Таким образом, сложность этого вычисления равна ${\displaystyle \Omega (D^{n})}$ ${\displaystyle \Omega (D^{n})>D^{\Omega (n)}.}$ ${\displaystyle O(D^{n}).}$ ${\displaystyle O(D^{n})^{O(1)}=D^{O(n)}.}$

Худшая сложность вычисления базиса Грёбнера дважды экспоненциальна по n . Точнее, сложность ограничена сверху полиномом по Используя немного обозначений o , она, следовательно, ограничена С другой стороны, были приведены примеры редуцированных базисов Грёбнера, содержащих полиномы степени или содержащих элементы. Поскольку каждый алгоритм для вычисления базиса Грёбнера должен записывать свой результат, это дает нижнюю границу сложности. ${\textstyle d^{2^{n}}.}$ ${\textstyle d^{2^{n+o(n)}}.}$ ${\textstyle d^{2^{\Omega (n)}},}$ ${\textstyle d^{2^{\Omega (n)}}}$

Базис Грёбнера является EXPSPACE-полным . ^[7]

Обобщения

Концепция и алгоритмы базисов Грёбнера были обобщены на подмодули свободных модулей над кольцом многочленов. Фактически, если L — свободный модуль над кольцом R , то можно рассматривать прямую сумму как кольцо, определив произведение двух элементов L как 0 . Это кольцо можно отождествить с , где — базис L . Это позволяет отождествить подмодуль L , порожденный с идеалом , порожденным и произведениями , . Если R — кольцо многочленов, это сводит теорию и алгоритмы базисов Грёбнера модулей к теории и алгоритмам базисов Грёбнера идеалов. ${\displaystyle R\oplus L}$ ${\displaystyle R[e_{1},\ldots ,e_{l}]/\left\langle \{e_{i}e_{j}|1\leq i\leq j\leq l\}\right\rangle }$ ${\displaystyle e_{1},\ldots ,e_{l}}$ ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle R[e_{1},\ldots ,e_{l}]}$ ${\displaystyle g_{1},\ldots ,g_{k}}$ ${\displaystyle e_{i}e_{j}}$ ${\displaystyle 1\leq i\leq j\leq l}$

Концепция и алгоритмы базисов Грёбнера были также обобщены на идеалы над различными кольцами, коммутативными и нет, например, на кольца многочленов над главным кольцом идеалов или алгебры Вейля .

Области применения

Коды исправления ошибок

Базис Грёбнера был применён в теории кодов с исправлением ошибок для алгебраического декодирования. Используя вычисление базиса Грёбнера на различных формах уравнений с исправлением ошибок, были разработаны методы декодирования для исправления ошибок циклических кодов, ^[8] аффинных многообразных кодов, ^[9] алгебро-геометрических кодов и даже общих линейных блочных кодов. ^[10] Применение базиса Грёбнера в алгебраическом декодировании по-прежнему является областью исследований теории канального кодирования.

Смотрите также

• Лемма Бергмана о алмазе , расширение базисов Грёбнера на некоммутативные кольца
• Более серьезная основа
• Джанет базис
• Регулярные цепочки , альтернативный способ представления алгебраических множеств

Ссылки

1. Lazard, Daniel (1983). "Gröbner bases, Gaussian exception and resolution of systems of algebraic conditions". Computer Algebra . Lecture Notes in Computer Science. Vol. 162. pp. 146–156. doi :10.1007/3-540-12868-9_99. ISBN 978-3-540-12868-7.
2. Реншух, Бодо; Ролофф, Хартмут; Распутин, Георгий Г.; Абрамсон, Михаил (июнь 2003 г.). «Вклад в конструктивную теорию полиномиальных идеалов XXIII: забытые работы ленинградского математика Н. М. Гюнтера по теории полиномиальных идеалов» (PDF) . SIGSAM Bull . 37 (2): 35–48. doi :10.1145/944567.944569. S2CID  1819694.
3. Кокс, Дэвид А .; Литтл, Джон; О'Ши, Донал (1997). Идеалы, многообразия и алгоритмы: введение в вычислительную алгебраическую геометрию и коммутативную алгебру . Springer. ISBN 0-387-94680-2.
4. Коллар, Стефан; Калькбренер, Майкл; Молл, Дэниел (1997). «Преобразование оснований с помощью прогулки Грёбнера». Журнал символических вычислений . 24 (3–4). Эльзевир: 465–469. дои : 10.1006/jsco.1996.0145 .
5. Faugère, Jean-Charles ; Chenqi, Mou (2017). «Разреженные алгоритмы FGLM». Journal of Symbolic Computation . 80 . Elsevier: 538–569. arXiv : 1304.1238 . doi : 10.1016/j.jsc.2016.07.025 . S2CID  149627.
6. Berthomieu \first1=Jérémy; Eder, Christian; Safey El Din, Mohab (2021). Msolve: библиотека для решения полиномиальных систем. Международный симпозиум по символьным и алгебраическим вычислениям 2021 года. 46-й Международный симпозиум по символьным и алгебраическим вычислениям. Санкт-Петербург, Россия. arXiv : 2104.03572 . doi :10.1145/3452143.3465545.{{cite conference}}: CS1 maint: numeric names: authors list (link)
7. Майр, Эрнст В. (сентябрь 1997 г.), «Некоторые результаты сложности для полиномиальных идеалов», Журнал сложности , 13 (3): 303–325, doi : 10.1006/jcom.1997.0447
8. Чен, X.; Рид, IS; Хеллесет, T.; Труонг, TK (1994). «Использование базисов Грёбнера для декодирования двоичных циклических кодов вплоть до истинного минимального расстояния». Труды IEEE по теории информации . 40 (5): 1654–61. doi :10.1109/18.333885.
9. Фицджеральд, Дж.; Лакс, РФ (1998). «Декодирование аффинных кодов с использованием базисов Грёбнера». Designs, Codes and Cryptography . 13 (2): 147–158. doi :10.1023/A:1008274212057. S2CID  2515114.
10. Булыгин, С.; Пелликаан, Р. (2009). «Декодирование линейных кодов с исправлением ошибок до половины минимального расстояния с базисами Грёбнера». Базисы Грёбнера, кодирование и криптография . Springer . стр. 361–5. ISBN 978-3-540-93805-7.

Дальнейшее чтение

• Адамс, Уильям В.; Лустаунау, Филипп (1994). Введение в базисы Грёбнера . Аспирантура по математике . Том 3. Американское математическое общество . ISBN 0-8218-3804-0.
• Ли, Хуэйши (2011). Базисы Грёбнера в теории колец . World Scientific . ISBN 978-981-4365-13-0.
• Беккер, Томас; Вайспфеннинг, Фолькер (1998). Базисы Грёбнера: вычислительный подход к коммутативной алгебре . Graduate Texts in Mathematics. Vol. 141. Springer. ISBN 0-387-97971-9.
• Бухбергер, Бруно (1965). Алгоритм нахождения базисных элементов кольца вычетов нульмерного полиномиального идеала (PDF) (PhD). Университет Инсбрука. — (2006). "Докторская диссертация Бруно Бухбергера 1965 г.: Алгоритм нахождения базисных элементов кольца классов вычетов нульмерного полиномиального идеала". Журнал символических вычислений . 41 (3–4). Перевод Абрамсона, М.: 471–511. doi : 10.1016/j.jsc.2005.09.007 . [Это тезис Бухбергера об изобретении базисов Грёбнера.]
• Бухбергер, Бруно (1970). «Алгоритмический критерий разрешимости системы алгебраических уравнений» (PDF) . Математические уравнения . 4 : 374–383. дои : 10.1007/BF01844169. S2CID  189834323. (Это журнальная публикация диссертации Бухбергера.) Burchberger, B.; Winkler, F., ред. (26 февраля 1998 г.). "Алгоритмический критерий разрешимости системы алгебраических уравнений". Gröbner Bases and Applications . London Mathematical Society Lecture Note Series. Том 251. Cambridge University Press. С. 535–545. ISBN 978-0-521-63298-0.
• Бухбергер, Бруно; Кауэрс, Мануэль (2010). «Базисы Грёбнера». Scholarpedia . 5 (10): 7763. Bibcode :2010SchpJ...5.7763B. doi : 10.4249/scholarpedia.7763 .
• Фрёберг, Ральф (1997). Введение в базисы Грёбнера . Уайли. ISBN 0-471-97442-0.
• Sturmfels, Bernd (ноябрь 2005 г.). "Что такое ... базис Грёбнера?" (PDF) . Notices of the American Mathematical Society . 52 (10): 1199–1200, краткое введение{{cite journal}}: CS1 maint: postscript (link)
• Ширшов, Анатолий И. (1999). "Некоторые алгоритмические проблемы для алгебр Ли" (PDF) . ACM SIGSAM Bulletin . 33 (2): 3–6. doi :10.1145/334714.334715. S2CID  37070503.(пер. с Сиб. мат. ж. Сибирский математический журнал 3 (1962), 292–296).
• Ашенбреннер, Маттиас ; Хиллар, Кристофер (2007). «Конечная генерация симметричных идеалов». Труды Американского математического общества . 359 (11): 5171–92. arXiv : math/0411514 . doi : 10.1090/S0002-9947-07-04116-5 . S2CID  5656701.(о бесконечномерных базисах Грёбнера для колец многочленов от бесконечного числа неизвестных).

Внешние ссылки

• Реализация алгоритма F4 самим Фожером
• «Базис Грёбнера», Энциклопедия математики , EMS Press , 2001 [1994]
• Бухбергер, Б. (2003). "Gröbner Bases: A Short Introduction for Systems Theories" (PDF) . В Moreno-Diaz, R.; Бухбергер, Б.; Фрейре, Дж. (ред.). Computer Aided Systems Theory — EUROCAST 2001: A Selection of Papers from the 8th International Workshop on Computer Aided Systems Theory. Springer. стр. 1–19. ISBN 978-3-540-45654-4.
• Бухбергер, Б.; Заплетал, А. «Библиография по основам Грёбнера».
• Страница сравнительных временных характеристик для программного обеспечения Gröbner Bases
• Профессор Бруно Бухбергер Бруно Бухбергер
• Вайсштейн, Эрик В. «Базис Грёбнера». Математический мир .
• Введение в теорию Гребнера на Scholarpedia