Крутящий момент

Поворотная сила вокруг оси

В физике и механике крутящий момент является вращательным аналогом линейной силы . ^[1] Его также называют моментом силы (также сокращенно моментом ). Символом крутящего момента обычно является строчная греческая буква тау . Когда его называют моментом силы, его обычно обозначают буквой M. Так же, как линейная сила является толчком или тягой, приложенной к телу, крутящий момент можно рассматривать как скручивание, приложенное к объекту относительно выбранной точки; например, закручивание винта использует крутящий момент, который прикладывается отверткой, вращающейся вокруг своей оси . Например, сила в три ньютона, приложенная на расстоянии двух метров от точки опоры, создает такой же крутящий момент, как сила в один ньютон, приложенная на расстоянии шести метров от точки опоры. ${\displaystyle {\boldsymbol {\tau }}}$

История

Термин «крутящий момент» (от лат. torquēre , «скручивать»), как говорят, был предложен Джеймсом Томсоном и появился в печати в апреле 1884 года. ^{[2] [3] [4]} Использование этого термина засвидетельствовано в том же году Сильванусом П. Томпсоном в первом издании «Динамо-электрических машин» . ^[4] Томпсон мотивирует этот термин следующим образом: ^[3]

Так же, как ньютоновское определение силы — это то, что производит или стремится производить движение (вдоль линии), так и крутящий момент можно определить как то, что производит или стремится производить кручение (вокруг оси). Лучше использовать термин, который рассматривает это действие как единую определенную сущность, чем использовать такие термины, как « пара » и « момент », которые предполагают более сложные идеи. Единое понятие кручения, применяемое для поворота вала, лучше, чем более сложное понятие приложения линейной силы (или пары сил) с определенным рычагом.

Сегодня крутящий момент обозначается с использованием разного словаря в зависимости от географического положения и области изучения. Эта статья следует определению, используемому в физике США в использовании слова крутящий момент . ^[5]

В машиностроении Великобритании и США крутящий момент называют моментом силы , обычно сокращая его до момента . ^[6] Эту терминологию можно проследить по крайней мере до 1811 года в «Traité de mécanique» Симеона Дени Пуассона . [ ^7] Английский перевод работы Пуассона появился в 1842 году.

Определение и связь с другими физическими величинами

Частица находится в положении r относительно своей оси вращения. Когда к частице приложена сила F , только перпендикулярная составляющая F _⊥ создает крутящий момент. Этот крутящий момент τ = r × F имеет величину τ = | r | | F _⊥ | = | r | | F | sin θ и направлен наружу от страницы.

Сила, приложенная перпендикулярно рычагу, умноженная на ее расстояние от точки опоры рычага (длину плеча рычага ), является его крутящим моментом. Таким образом, крутящий момент определяется как произведение величины перпендикулярной составляющей силы и расстояния линии действия силы от точки, вокруг которой он определяется. В трех измерениях крутящий момент является псевдовектором ; для точечных частиц он задается перекрестным произведением вектора смещения и вектора силы. Направление крутящего момента можно определить с помощью правила правой руки : если пальцы правой руки согнуты от направления плеча рычага к направлению силы, то большой палец указывает в направлении крутящего момента. ^[8] Из этого следует, что вектор крутящего момента перпендикулярен как векторам положения , так и силы и определяет плоскость, в которой лежат два вектора. Результирующее направление вектора крутящего момента определяется правилом правой руки. Поэтому любая сила, направленная параллельно вектору положения частицы, не создает крутящего момента. ^{[9] [10]} Величина крутящего момента, приложенного к твердому телу, зависит от трех величин: приложенной силы, вектора плеча рычага ^[11], соединяющего точку, относительно которой измеряется крутящий момент, с точкой приложения силы, и угла между векторами силы и плеча рычага. В символах:

$${\displaystyle {\boldsymbol {\tau }}=\mathbf {r} \times \mathbf {F} \implies \tau =rF_{\perp }=rF\sin \theta }$$

где

• ${\displaystyle {\boldsymbol {\tau }}}$- вектор крутящего момента, - величина крутящего момента, ${\displaystyle \tau }$
• ${\displaystyle \mathbf {r} }$— вектор положения (вектор от точки, относительно которой измеряется крутящий момент, до точки, где приложена сила), а r — величина вектора положения,
• ${\displaystyle \mathbf {F} }$— вектор силы, F — величина вектора силы, а F _⊥ — величина силы, направленной перпендикулярно положению частицы,
• ${\displaystyle \times }$обозначает векторное произведение , которое создает вектор, перпендикулярный как r , так и F, следуя правилу правой руки ,
• ${\displaystyle \theta }$угол между вектором силы и вектором плеча рычага.

Единицей крутящего момента в системе СИ является ньютон-метр (Н⋅м). Подробнее о единицах крутящего момента см. в разделе Единицы.

Связь с моментом импульса

Чистый крутящий момент тела определяет скорость изменения момента импульса тела ,

$${\displaystyle {\boldsymbol {\tau }}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}}$$

где L — вектор момента импульса, а t — время. Для движения точечной частицы,

$${\displaystyle \mathbf {L} =I{\boldsymbol {\omega }},}$$

где - момент инерции , а ω - псевдовектор орбитальной угловой скорости . Отсюда следует, что ${\textstyle I=mr^{2}}$

$${\displaystyle {\boldsymbol {\tau }}_{\mathrm {net} }=I_{1}{\dot {\omega _{1}}}{\hat {\boldsymbol {e_{1}}}}+I_{2}{\dot {\omega _{2}}}{\hat {\boldsymbol {e_{2}}}}+I_{3}{\dot {\omega _{3}}}{\hat {\boldsymbol {e_{3}}}}+I_{1}\omega _{1}{\frac {d{\hat {\boldsymbol {e_{1}}}}}{dt}}+I_{2}\omega _{2}{\frac {d{\hat {\boldsymbol {e_{2}}}}}{dt}}+I_{3}\omega _{3}{\frac {d{\hat {\boldsymbol {e_{3}}}}}{dt}}=I{\boldsymbol {\dot {\omega }}}+{\boldsymbol {\omega }}\times (I{\boldsymbol {\omega }})}$$

с использованием производной вектора это Это уравнение является вращательным аналогом второго закона Ньютона для точечных частиц и справедливо для любого типа траектории. В некоторых простых случаях, таких как вращающийся диск, где только момент инерции на вращающейся оси равен, вращательный второй закон Ньютона может быть где . $${\displaystyle {d{\boldsymbol {\hat {e_{i}}}} \over dt}={\boldsymbol {\omega }}\times {\boldsymbol {\hat {e_{i}}}}}$$ $${\displaystyle {\boldsymbol {\tau }}=I{\boldsymbol {\alpha }}}$$ ${\displaystyle {\boldsymbol {\alpha }}={\dot {\boldsymbol {\omega }}}}$

Доказательство эквивалентности определений

Определение момента импульса для отдельной точечной частицы: где p — линейный импульс частицы , а r — радиус-вектор из начала координат. Производная по времени от этого равна: $${\displaystyle \mathbf {L} =\mathbf {r} \times \mathbf {p} }$$

$${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times \mathbf {p} .}$$

Этот результат можно легко доказать, разделив векторы на компоненты и применив правило произведения . Но поскольку скорость изменения линейного импульса — это сила , а скорость изменения положения — это скорость , ${\textstyle \mathbf {F} }$ ${\textstyle \mathbf {v} }$

$${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} +\mathbf {v} \times \mathbf {p} }$$

Перекрестное произведение импульса на связанную с ним скорость равно нулю, поскольку скорость и импульс параллельны, поэтому второй член равен нулю. Следовательно, крутящий момент на частице равен первой производной ее углового момента по времени. Если приложено несколько сил, то согласно второму закону Ньютона следует, что ${\displaystyle \mathbf {p} }$ ${\displaystyle \mathbf {v} }$ $${\displaystyle {\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {r} \times \mathbf {F} _{\mathrm {net} }={\boldsymbol {\tau }}_{\mathrm {net} }.}$$

Это общее доказательство для точечных частиц, но его можно обобщить на систему точечных частиц, применив приведенное выше доказательство к каждой из точечных частиц, а затем просуммировав по всем точечным частицам. Аналогично, доказательство можно обобщить на непрерывную массу, применив приведенное выше доказательство к каждой точке внутри массы, а затем проинтегрировав по всей массе.

Производные крутящего момента

В физике ротатум — это производная крутящего момента по времени ^[12]

${\displaystyle \mathbf {P} ={\frac {\mathrm {d} {\boldsymbol {\tau }}}{\mathrm {d} t}},}$

где τ — крутящий момент.

Это слово произошло от латинского слова rotātus, означающего «вращать», но термин rotatum не является общепризнанным, но широко используется. Не существует общепризнанного лексикона для обозначения последовательных производных от rotatum, хотя иногда и высказывались различные предложения.

Используя определение крутящего момента через векторное произведение, альтернативное выражение для вращательного момента выглядит следующим образом:

${\displaystyle \mathbf {P} =\mathbf {r} \times {\frac {\mathrm {d} \mathbf {F} }{\mathrm {d} t}}+{\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times \mathbf {F} .}$

Поскольку скорость изменения силы равна рывку , а скорость изменения положения равна скорости , выражение можно упростить до: ${\textstyle \mathbf {Y} }$ ${\textstyle \mathbf {v} }$

${\displaystyle \mathbf {P} =\mathbf {r} \times \mathbf {Y} +\mathbf {v} \times \mathbf {F} .}$

Связь с властью и энергией

Закон сохранения энергии также может быть использован для понимания крутящего момента. Если силе разрешено действовать на расстоянии, она совершает механическую работу . Аналогично, если крутящему моменту разрешено действовать через угловое смещение, он совершает работу. Математически, для вращения вокруг фиксированной оси через центр масс , работа W может быть выражена как

W знак равно ∫ θ 1 θ 2 τ d θ , {\ displaystyle W = \ int _ {\ theta _ {1}} ^ {\ theta _ {2}} \ tau \ \ mathrm {d} \ theta,}

где τ — крутящий момент, а θ ₁ и θ ₂ представляют (соответственно) начальное и конечное угловые положения тела. ^[13]

Из принципа работы-энергии следует , что W также представляет собой изменение вращательной кинетической энергии E _r тела, определяемое выражением

E р знак равно 1 2 я ω 2 , {\ displaystyle E _ {\ mathrm {r}} = {\ tfrac {1} {2}} I \ omega ^ {2},}

где I — момент инерции тела, а ω — его угловая скорость . ^[13]

Мощность — это работа за единицу времени , определяемая по формуле

п знак равно τ ⋅ ω , {\displaystyle P={\boldsymbol {\tau }}\cdot {\boldsymbol {\omega }},}

где P — мощность, τ — крутящий момент, ω — угловая скорость , а представляет собой скалярное произведение . ${\displaystyle \cdot }$

Алгебраически уравнение можно перестроить для вычисления крутящего момента для заданной угловой скорости и выходной мощности. Мощность, впрыскиваемая крутящим моментом, зависит только от мгновенной угловой скорости, а не от того, увеличивается ли угловая скорость, уменьшается или остается постоянной, пока применяется крутящий момент (это эквивалентно линейному случаю, когда мощность, впрыскиваемая силой, зависит только от мгновенной скорости, а не от результирующего ускорения, если таковое имеется).

Доказательство

Работа, совершаемая переменной силой, действующей на конечное линейное перемещение, определяется путем интегрирования силы по элементарному линейному перемещению. ${\displaystyle s}$ ${\displaystyle \mathrm {d} \mathbf {s} }$

$${\displaystyle W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} \mathbf {s} }$$

Однако бесконечно малое линейное смещение связано с соответствующим угловым смещением и радиусом-вектором как ${\displaystyle \mathrm {d} \mathbf {s} }$ ${\displaystyle \mathrm {d} {\boldsymbol {\theta }}}$ ${\displaystyle \mathbf {r} }$

$${\displaystyle \mathrm {d} \mathbf {s} =\mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r} }$$

Подстановка в приведенное выше выражение для работы дает $${\displaystyle W=\int _{s_{1}}^{s_{2}}\mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r} }$$

Выражение внутри интеграла представляет собой скалярное тройное произведение , но согласно определению крутящего момента и поскольку параметр интегрирования был изменен с линейного смещения на угловое смещение, уравнение становится ${\displaystyle \mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}\times \mathbf {r} =\mathbf {r} \times \mathbf {F} \cdot \mathrm {d} {\boldsymbol {\theta }}}$

$${\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}{\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}}$$

Если крутящий момент и угловое смещение имеют одно и то же направление, то скалярное произведение сводится к произведению величин, т. е. давая ${\displaystyle {\boldsymbol {\tau }}\cdot \mathrm {d} {\boldsymbol {\theta }}=\left|{\boldsymbol {\tau }}\right|\left|\mathrm {d} {\boldsymbol {\theta }}\right|\cos 0=\tau \,\mathrm {d} \theta }$

$${\displaystyle W=\int _{\theta _{1}}^{\theta _{2}}\tau \,\mathrm {d} \theta }$$

Принцип моментов

Принцип моментов, также известный как теорема Вариньона (не путать с геометрической теоремой с тем же названием), гласит, что результирующий крутящий момент, возникающий вследствие действия нескольких сил, приложенных к одной точке, равен сумме вносящих вклад крутящих моментов:

$${\displaystyle \tau =\mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\ldots +\mathbf {r} _{N}\times \mathbf {F} _{N}.}$$

Из этого следует, что крутящие моменты, возникающие в результате действия N сил вокруг оси на объект, уравновешиваются, когда

$${\displaystyle \mathbf {r} _{1}\times \mathbf {F} _{1}+\mathbf {r} _{2}\times \mathbf {F} _{2}+\ldots +\mathbf {r} _{N}\times \mathbf {F} _{N}=\mathbf {0} .}$$

Единицы

Крутящий момент имеет размерность силы, умноженной на расстояние , символически T ⁻² L ² M, и эти основные размеры такие же , как у энергии или работы . Официальная литература СИ указывает ньютон-метр , правильно обозначаемый как Н⋅м, как единицу для крутящего момента; хотя это размерно эквивалентно джоулю , который является единицей энергии, последний никогда не может использоваться для крутящего момента. ^{[14] [15]} В случае крутящего момента единица назначается вектору , тогда как для энергии она назначается скаляру . Это означает, что размерная эквивалентность ньютон-метра и джоуля может быть применена в первом случае, но не во втором. Эта проблема решается в ориентационном анализе , который рассматривает радиан как базовую единицу, а не как безразмерную единицу. ^[16]

Традиционными имперскими единицами измерения крутящего момента являются фунт-фут (lbf-ft) или, для малых значений, фунт-дюйм (lbf-in). В США крутящий момент чаще всего называют фут -фунтом (обозначается как lb-ft или ft-lb) и дюйм-фунтом (обозначается как in-lb). ^{[17] [18]} Практикующие специалисты полагаются на контекст и дефис в аббревиатуре, чтобы знать, что они относятся к крутящему моменту, а не к энергии или моменту массы (как правильно подразумевает символика ft-lb).

Перевод в другие единицы

Коэффициент преобразования может быть необходим при использовании различных единиц мощности или крутящего момента. Например, если вместо угловой скорости (единица: радиан в секунду) используется скорость вращения (единица: оборот в минуту или секунду), мы должны умножить на 2π радиан на оборот. В следующих формулах P — мощность, τ — крутящий момент, а ν ( греческая буква ню ) — скорость вращения.

$${\displaystyle P=\tau \cdot 2\pi \cdot \nu }$$

Показаны единицы:

$${\displaystyle P_{\rm {W}}=\tau _{\rm {N{\cdot }m}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/s}}}$$

Разделив минуту на 60 секунд, получаем следующее.

$${\displaystyle P_{\rm {W}}={\frac {\tau _{\rm {N{\cdot }m}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}}{\rm {60~s/min}}}}$$

где скорость вращения измеряется в оборотах в минуту (об/мин).

Некоторые люди (например, американские инженеры-автомобилестроители) используют лошадиные силы (механические) для мощности, фут-фунты (lbf⋅ft) для крутящего момента и об/мин для скорости вращения. Это приводит к изменению формулы на:

$${\displaystyle P_{\rm {hp}}={\frac {\tau _{\rm {lbf{\cdot }ft}}\cdot 2\pi _{\rm {rad/rev}}\cdot \nu _{\rm {rev/min}}}{33,000}}.}$$

Приведенная ниже константа (в футо-фунтах в минуту) изменяется в зависимости от определения лошадиной силы; например, при использовании метрической лошадиной силы она становится приблизительно равной 32 550.

Использование других единиц (например, БТЕ в час для мощности) потребует другого специального коэффициента пересчета.

Вывод

Для вращающегося объекта линейное расстояние, пройденное по окружности вращения, является произведением радиуса на пройденный угол. То есть: линейное расстояние = радиус × угловое расстояние. И по определению, линейное расстояние = линейная скорость × время = радиус × угловая скорость × время.

По определению крутящего момента: крутящий момент = радиус × сила. Мы можем переставить это так, чтобы определить силу = крутящий момент ÷ радиус. Эти два значения можно подставить в определение мощности :

$${\displaystyle {\begin{aligned}{\text{power}}&={\frac {{\text{force}}\cdot {\text{linear distance}}}{\text{time}}}\\[6pt]&={\frac {\left({\dfrac {\text{torque}}{r}}\right)\cdot (r\cdot {\text{angular speed}}\cdot t)}{t}}\\[6pt]&={\text{torque}}\cdot {\text{angular speed}}.\end{aligned}}}$$

Радиус r и время t выпали из уравнения. Однако угловая скорость должна быть в радианах за единицу времени, в соответствии с предполагаемой прямой связью между линейной скоростью и угловой скоростью в начале вывода. Если скорость вращения измеряется в оборотах за единицу времени, линейная скорость и расстояние увеличиваются пропорционально на 2 π в приведенном выше выводе, чтобы получить:

$${\displaystyle {\text{power}}={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}.\,}$$

Если крутящий момент выражен в ньютон-метрах, а скорость вращения в оборотах в секунду, приведенное выше уравнение дает мощность в ньютон-метрах в секунду или ваттах. Если используются имперские единицы, и если крутящий момент выражен в фунтах-силах-футах, а скорость вращения в оборотах в минуту, приведенное выше уравнение дает мощность в футах-фунтах-силах в минуту. Затем форма лошадиных сил уравнения выводится путем применения коэффициента преобразования 33 000 фут⋅фунт-сила/мин на лошадиную силу:

$${\displaystyle {\begin{aligned}{\text{power}}&={\text{torque}}\cdot 2\pi \cdot {\text{rotational speed}}\cdot {\frac {{\text{ft}}{\cdot }{\text{lbf}}}{\text{min}}}\cdot {\frac {\text{horsepower}}{33,000\cdot {\frac {{\text{ft}}\cdot {\text{lbf}}}{\text{min}}}}}\\[6pt]&\approx {\frac {{\text{torque}}\cdot {\text{RPM}}}{5,252}}\end{aligned}}}$$

потому что ${\displaystyle 5252.113122\approx {\frac {33,000}{2\pi }}.\,}$

Особые случаи и другие факты

Формула плеча момента

Диаграмма плеча момента

Очень полезный частный случай, часто приводимый в качестве определения крутящего момента в областях, отличных от физики, выглядит следующим образом:

$${\displaystyle \tau =({\text{moment arm}})({\text{force}}).}$$

Конструкция «плеча момента» показана на рисунке справа вместе с векторами r и F, упомянутыми выше. Проблема с этим определением в том, что оно не дает направления крутящего момента, а только величину, и, следовательно, его трудно использовать в трехмерных случаях. Если сила перпендикулярна вектору смещения r , плечо момента будет равно расстоянию до центра, а крутящий момент будет максимальным для данной силы. Уравнение для величины крутящего момента, возникающего из-за перпендикулярной силы:

$${\displaystyle \tau =({\text{distance to centre}})({\text{force}}).}$$

Например, если человек прикладывает силу 10 Н к концу гаечного ключа длиной 0,5 м (или силу 10 Н, действующую на расстоянии 0,5 м от точки поворота гаечного ключа любой длины), крутящий момент составит 5 Н⋅м — при условии, что человек перемещает гаечный ключ, прикладывая силу в плоскости движения и перпендикулярно ключу.

Крутящий момент, вызванный двумя противоположными силами F _g и − F _g, вызывает изменение углового момента L в направлении этого крутящего момента. Это заставляет волчок прецессировать .

Статическое равновесие

Для того чтобы объект находился в статическом равновесии , не только сумма сил должна быть равна нулю, но и сумма крутящих моментов (моментов) относительно любой точки. Для двумерной ситуации с горизонтальными и вертикальными силами сумма требуемых сил — это два уравнения: Σ H = 0 и Σ V = 0 , а крутящий момент — третье уравнение: Σ τ = 0. То есть, для решения статически определенных задач равновесия в двух измерениях используются три уравнения.

Чистая сила против крутящего момента

Когда чистая сила, действующая на систему, равна нулю, крутящий момент, измеренный из любой точки пространства, одинаков. Например, крутящий момент на контуре с током в однородном магнитном поле одинаков независимо от точки отсчета. Если чистая сила не равна нулю, а является крутящим моментом, измеренным из , то крутящий момент, измеренный из , является ${\displaystyle \mathbf {F} }$ ${\displaystyle {\boldsymbol {\tau }}_{1}}$ ${\displaystyle \mathbf {r} _{1}}$ ${\displaystyle \mathbf {r} _{2}}$ $${\displaystyle {\boldsymbol {\tau }}_{2}={\boldsymbol {\tau }}_{1}+(\mathbf {r} _{2}-\mathbf {r} _{1})\times \mathbf {F} }$$

Крутящий момент машины

Кривая крутящего момента мотоцикла («BMW K 1200 R 2005»). Горизонтальная ось показывает скорость вращения (в об/мин ), которую вращает коленчатый вал , а вертикальная ось — крутящий момент (в ньютон-метрах ), который двигатель способен обеспечить на этой скорости.

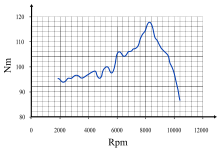
Крутящий момент является частью базовой спецификации двигателя : выходная мощность двигателя выражается как его крутящий момент, умноженный на угловую скорость приводного вала. Двигатели внутреннего сгорания создают полезный крутящий момент только в ограниченном диапазоне скоростей вращения (обычно от 1000 до 6000  об/мин для небольшого автомобиля). Можно измерить изменяющийся выходной крутящий момент в этом диапазоне с помощью динамометра и показать его в виде кривой крутящего момента. Паровые двигатели и электродвигатели, как правило, создают максимальный крутящий момент вблизи нуля об/мин, причем крутящий момент уменьшается по мере увеличения скорости вращения (из-за увеличения трения и других ограничений). Поршневые паровые двигатели и электродвигатели могут запускать тяжелые грузы с нуля об/мин без сцепления .

На практике взаимосвязь между мощностью и крутящим моментом можно наблюдать в велосипедах : велосипеды обычно состоят из двух колес, передней и задней передач (называемых звездочками ), зацепленных с цепью , и механизма переключения передач , если система трансмиссии велосипеда позволяет использовать несколько передаточных чисел (т. е. многоскоростной велосипед ), все из которых прикреплены к раме . Велосипедист , человек, который едет на велосипеде, обеспечивает входную мощность, вращая педали, тем самым проворачивая переднюю звездочку (обычно называемую цепной звездочкой ). Входная мощность, обеспечиваемая велосипедистом, равна произведению угловой скорости (т. е. количества оборотов педалей в минуту, умноженного на 2π ) и крутящего момента на оси кривошипной системы велосипеда . Трансмиссия велосипеда передает входную мощность на колесо , которое, в свою очередь, передает полученную мощность на дорогу в качестве выходной мощности велосипеда. В зависимости от передаточного числа велосипеда _{входная} пара (крутящий момент, угловая скорость) преобразуется в _{выходную} пару (крутящий момент, угловая скорость). При использовании большей задней передачи или при переключении на пониженную передачу в многоскоростных велосипедах угловая скорость колес уменьшается, а крутящий момент увеличивается, произведение которого (т. е. мощность) не изменяется.

Умножитель крутящего момента

Крутящий момент можно увеличить тремя способами: расположив точку опоры таким образом, чтобы длина рычага увеличилась; используя более длинный рычаг; или используя редуктор или коробку передач . Такой механизм увеличивает крутящий момент, поскольку скорость вращения уменьшается.

Смотрите также

• Момент
• Изгибающий момент
• Перевод единиц
• Момент трения
• Механическое равновесие
• Динамика твердого тела
• Статика
• Гидротрансформатор
• Ограничитель крутящего момента
• Динамометрическая отвертка
• Тестер крутящего момента
• Динамометрический ключ
• Торсион (механика)

Ссылки

1. Serway, RA и Jewett, JW Jr. (2003). Физика для ученых и инженеров . 6-е изд. Brooks Cole. ISBN  0-534-40842-7 .
2. Томсон, Джеймс; Лармор, Джозеф (1912). Сборник статей по физике и технике. University Press. стр. civ.
3. Thompson, Silvanus Phillips (1893). Динамоэлектрические машины: руководство для студентов-электротехников (4-е изд.). Нью-Йорк, Harvard Publishing Co., стр. 108.
4. "крутящий момент". Оксфордский словарь английского языка . 1933.
5. Физика для инженерии Хендрикса, Субрамони и Ван Блерка, Chinappi, стр. 148, веб-ссылка. Архивировано 11 июля 2017 г. на Wayback Machine.
6. Кейн, Т. Р. Кейн и Д. А. Левинсон (1985). Динамика, теория и приложения, стр. 90–99: Бесплатная загрузка Архивировано 19 июня 2015 г. на Wayback Machine .
7. Пуассон, Симеон-Дени (1811). Traité de mécanique, первый том. п. 67.
8. "Правило правой руки для крутящего момента". Архивировано из оригинала 2007-08-19 . Получено 2007-09-08 .
9. Холлидей, Дэвид; Резник, Роберт (1970). Основы физики . John Wiley & Sons. С. 184–85.
10. Найт, Рэндалл; Джонс, Брайан; Филд, Стюарт (2016). College Physics: A Strategic Approach (3rd technology update ed.). Бостон: Pearson. стр. 199. ISBN 9780134143323. OCLC  922464227.
11. Типлер, Пол (2004). Физика для ученых и инженеров: механика, колебания и волны, термодинамика (5-е изд.). WH Freeman. ISBN 0-7167-0809-4.
12. «Исследование взаимодействия человека и робота в промышленных условиях: осведомленность, интеллект и соответствие».
13. Kleppner, Daniel; Kolenkow, Robert (1973). Введение в механику . McGraw-Hill. стр. 267–268. ISBN 9780070350489.
14. С официального сайта СИ Архивировано 19 апреля 2021 г. на Wayback Machine , Международная система единиц – 9-е издание – Текст на английском языке Раздел 2.3.4: «Например, величина крутящего момента является перекрестным произведением вектора положения и вектора силы. Единица СИ – ньютон-метр. Несмотря на то, что крутящий момент имеет ту же размерность, что и энергия (единица СИ – джоуль), джоуль никогда не используется для выражения крутящего момента».
15. "SI brochure Ed. 9, Section 2.3.4" (PDF) . Bureau International des Poids et Mesures. 2019. Архивировано (PDF) из оригинала 2020-07-26 . Получено 2020-05-29 .
16. Пейдж, Честер Х. (1979). "Опровержение "Групповых свойств величин и единиц" де Бура"". Американский журнал физики . 47 (9): 820. Bibcode : 1979AmJPh..47..820P. doi : 10.1119/1.11704.
17. "Dial Torque Wrenchs from Grainger". Grainger. 2020.Демонстрация того, что, как и в большинстве промышленных предприятий США, диапазоны крутящего момента указаны в фут-фунтах, а не в фунт-силах-футах.
18. Эрьявец, Джек (22 января 2010 г.). Механические коробки передач и трансмиссии: Учебное пособие . Cengage Learning. стр. 38. ISBN 978-1-4354-3933-7.

Внешние ссылки

• «Лошадиная мощность и крутящий момент». Архивировано 28.03.2007 на Wayback Machine. Статья, показывающая, как мощность, крутящий момент и передача влияют на производительность автомобиля.
• Крутящий момент и угловой момент при круговом движении в проекте PHYSNET.
• Интерактивное моделирование крутящего момента
• Преобразователь единиц крутящего момента
• Ощущение крутящего момента Архивировано 08.05.2021 в Wayback Machine Интерактивный порядок величин.