Гауссово целое число

В теории чисел гауссово целое число — это комплексное число , действительная и мнимая части которого являются целыми числами . Гауссовы целые числа, с обычным сложением и умножением комплексных чисел , образуют интегральную область , обычно записываемую как или ^[1] $\mathbf {Z} [я]$ $\mathbb {Z} [я].$

Гауссовы целые числа имеют много общих свойств с целыми числами: они образуют евклидову область и, таким образом, имеют евклидово деление и евклидов алгоритм ; это подразумевает уникальную факторизацию и множество связанных свойств. Однако гауссовы целые числа не имеют общего порядка , который уважает арифметику.

Гауссовы целые числа являются алгебраическими целыми числами и образуют простейшее кольцо квадратичных целых чисел .

Гауссовы целые числа названы в честь немецкого математика Карла Фридриха Гаусса .

Основные определения

Гауссовы целые числа — это набор ^[1]

\mathbf {Z} [i]=\{a+bi\mid a,b\in \mathbf {Z} \},\qquad {\text{ где }}i^{2}=-1.

Другими словами, гауссово целое число — это комплексное число , такое что его действительная и мнимая части являются целыми числами . Поскольку гауссовы целые числа замкнуты относительно сложения и умножения, они образуют коммутативное кольцо , которое является подкольцом поля комплексных чисел. Таким образом, это область целостности .

При рассмотрении в комплексной плоскости гауссовы целые числа образуют $двумерную$ целочисленную решетку .

Сопряженным числом гауссовского целого числа $a + bi$ является гауссовское целое число $a - bi$ .

Норма гауссовского целого числа равна его произведению на сопряженное ему число .

N(a+bi)=(a+bi)(a-bi)=a^{2}+b^{2}.

Норма гауссовского целого числа, таким образом, является квадратом его абсолютного значения как комплексного числа. Норма гауссовского целого числа является неотрицательным целым числом, которое является суммой двух квадратов . Таким образом, норма не может иметь вид $4 k + 3$ , где $k$ — целое число .

Норма мультипликативна , то есть имеет место ^[2]

N(zw)=N(z)N(w),

для каждой пары гауссовых целых чисел $z, w$ . Это можно показать напрямую или с помощью мультипликативного свойства модуля комплексных чисел.

Единицами кольца целых гауссовых чисел (то есть целых гауссовых чисел, мультипликативное обратное число которых также является целым гауссовым числом ) являются в точности целые гауссовы числа с нормой 1, то есть 1, –1, $i$ и $-$ $i$ . ^[3]

Евклидово деление

Визуализация максимального расстояния до некоторого гауссовского целого числа

Гауссовы целые числа имеют евклидово деление (деление с остатком), подобное делению целых чисел и многочленов . Это делает гауссовы целые числа евклидовой областью и подразумевает, что гауссовы целые числа разделяют с целыми числами и многочленами многие важные свойства, такие как существование евклидова алгоритма для вычисления наибольших общих делителей , тождество Безу , свойство главного идеала , лемма Евклида , теорема об уникальной факторизации и китайская теорема об остатках , все из которых можно доказать, используя только евклидово деление.

Алгоритм евклидова деления берет в кольце гауссовых целых чисел делимое $a$ и делитель $b \neq 0$ и выдает частное $q$ и остаток $r,$ такие что

a=bq+r\quad {\text{и}}\quad N(r)<N(b).

На самом деле, остаток можно сделать меньше:

a=bq+r\quad {\text{и}}\quad N(r)\leq {\frac {N(b)}{2}}.

Даже при таком лучшем неравенстве частное и остаток не обязательно будут уникальными, но можно уточнить выбор, чтобы гарантировать уникальность.

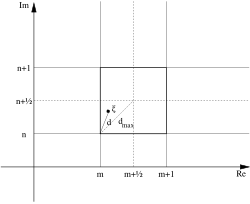
Чтобы доказать это, можно рассмотреть комплексное числовое отношение $x + iy = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠а/б⁠$ . Существуют уникальные целые числа $m$ и $n,$ такие что $- ⁠ 1 / 2 ⁠ < х - м \leq ⁠ 1 / 2 ⁠$ и $- ⁠ 1 / 2 ⁠ < у - н \leq ⁠ 1 / 2 ⁠$ , и таким образом $N (x - m + i (y - n)) \leq ⁠ 1 / 2 ⁠$ . Принимая $q = m + in$ , имеем

a=bq+r,

r=b{\bigl (}x-m+i(yn){\bigr )},

N(r)\leq {\frac {N(b)}{2}}.

Выбор $x - m$ и $y - n$ в полуоткрытом интервале требуется для уникальности. Это определение евклидова деления можно интерпретировать геометрически в комплексной плоскости (см. рисунок), заметив, что расстояние от комплексного числа $ξ$ до ближайшего гауссовского целого числа не превышает $⁠$ $\sqrt 2 / 2 ⁠$ .^[4]

Главные идеалы

Так как кольцо $G$ целых гауссовых чисел является евклидовой областью, $G$ является областью главных идеалов , что означает, что каждый идеал G является главным . Явно, идеал $I$ является подмножеством кольца $R$ таким, что каждая сумма элементов $I$ и каждое произведение элемента $I$ на элемент $R$ принадлежат $I.$ Идеал является главным, если он состоит из всех кратных одного элемента $g$ $,$ то есть имеет вид

\{gx\mid x\in G\}.

В этом случае говорят, что идеал порождается g или что $g$ $является$ генератором идеала .

Каждый идеал $I$ в кольце гауссовых целых чисел является главным, потому что, если выбрать в $I$ ненулевой элемент $g$ минимальной нормы, то для каждого элемента $x$ из $I$ остаток от евклидова деления $x$ на $g$ также принадлежит $I$ и имеет норму, меньшую, чем у $g$ ; из-за выбора $g$ эта норма равна нулю, и, следовательно, остаток также равен нулю. То есть, $x = qg$ , где $q$ — частное.

Для любого $g$ идеал, порожденный $g$ , также порождается любым ассоциированным элементом $g$ , то есть $g, gi, - g, - gi$ ; никакой другой элемент не порождает тот же идеал. Поскольку все образующие идеала имеют одну и ту же норму, норма идеала является нормой любого из его образующих.

В некоторых обстоятельствах полезно выбрать, раз и навсегда, генератор для каждого идеала. Для этого есть два классических способа, оба из которых рассматривают сначала идеалы нечетной нормы. Если $g = a + bi$ имеет нечетную норму $a 2 + b 2$ , то один из $a$ и $b$ нечетный, а другой четный. Таким образом, $g$ имеет ровно одного ассоциированного элемента с действительной частью $a,$ которая нечетна и положительна. В своей оригинальной статье Гаусс сделал другой выбор, выбрав единственный ассоциированный элемент таким образом, что остаток от его деления на $2 + 2 i$ равен единице. Фактически, поскольку $N (2 + 2 i) = 8$ , норма остатка не больше 4. Поскольку эта норма нечетна, а 3 не является нормой гауссовского целого числа, норма остатка равна единице, то есть остаток является единицей. Умножая $g$ на обратную этой единице величину, можно найти ассоциированный элемент, который имеет единицу в качестве остатка при делении на $2 + 2 i$ .

Если норма $g$ четная, то либо $g = 2 k h ,$ либо $g = 2 k h (1 + i)$ , где $k$ — положительное целое число, а $N (h)$ — нечетное. Таким образом, выбирается ассоциированный элемент $g$ для получения $h$ , который соответствует выбору ассоциированных элементов для элементов нечетной нормы.

Гауссовы простые числа

Поскольку гауссовы целые числа образуют область главных идеалов, они также образуют область уникальной факторизации . Это подразумевает, что гауссово целое число неприводимо (то есть оно не является произведением двух неединиц ) тогда и только тогда, когда оно является простым (то есть оно порождает простой идеал ).

Простые элементы Z $[$ $i$ $]$ также известны как гауссовы простые числа . Ассоциированное с гауссовым простым числом число также является гауссовым простым числом. Сопряженное с гауссовым простым числом число также является гауссовым простым числом $($ это подразумевает, что гауссовы простые числа симметричны относительно действительной и мнимой осей).

Положительное целое число является гауссовым простым числом тогда и только тогда, когда оно является простым числом , сравнимым с 3 по модулю 4 (то есть его можно записать как $4 n + 3$ , где $n —$ неотрицательное целое число) (последовательность A002145 в OEIS ). Остальные простые числа не являются гауссовыми простыми числами, но каждое из них является произведением двух сопряженных гауссовых простых чисел.

Гауссово целое число $a + bi$ является гауссовым простым тогда и только тогда, когда выполняется одно из следующих условий:

один из $a, b$ равен нулю, а абсолютное значение другого является простым числом вида $4 n + 3$ (где $n$ — неотрицательное целое число), или
оба числа не равны нулю, а $a 2 + b 2$ — простое число (которое не будет иметь вид $4 n + 3$ ).

Другими словами, гауссово целое число $m$ является гауссовым простым числом тогда и только тогда, когда либо его норма является простым числом, либо $m$ является произведением единицы ( $\pm1, \pm i$ ) и простого числа вида $4 n + 3$ .

Отсюда следует, что существует три случая факторизации простого натурального числа $p$ в гауссовых целых числах:

Если $p$ сравнимо с 3 по модулю 4, то оно является гауссовым простым числом; на языке алгебраической теории чисел говорят , что $p$ инертно в гауссовых целых числах.
Если $p$ сравнимо с 1 по модулю 4, то оно является произведением гауссовского простого числа на его сопряженное число, оба из которых являются неассоциированными гауссовыми простыми числами (ни одно из них не является произведением другого на единицу); говорят, что $p$ является разложенным простым числом в гауссовых целых числах. Например, $5 = (2 + i)(2 - i)$ и $13 = (3 + 2 i)(3 - 2 i)$ .
Если $p = 2$ , то $2 = (1 + i)(1 - i) = i (1 - i) 2$ ; то есть 2 — это произведение квадрата простого гауссовского числа на единицу; это единственное разветвленное простое число в гауссовых целых числах.

Уникальная факторизация

Как и для каждой уникальной области факторизации , каждое гауссово целое число может быть разложено на множители как произведение единицы и гауссовых простых чисел, и эта факторизация уникальна с точностью до порядка множителей и замены любого простого числа любым из его ассоциированных чисел (вместе с соответствующим изменением единичного множителя).

Если выбрать, раз и навсегда, фиксированное гауссово простое число для каждого класса эквивалентности ассоциированных простых чисел, и если взять только эти выбранные простые числа в факторизации, то получится факторизация, которая уникальна вплоть до порядка множителей. С выбором, описанным выше, результирующая уникальная факторизация имеет вид

u(1+i)^{e_{0}}{p_{1}}^{e_{1}}\cdots {p_{k}}^{e_{k}},

где $u$ — единица (то есть $u \in {1, -1, i, - i}$ ), $e 0$ и $k$ — неотрицательные целые числа, $e 1, \dots, e k$ — положительные целые числа, а $p 1, \dots, p k$ — различные гауссовские простые числа, такие, что в зависимости от выбора выбранных ассоциированных элементов,

либо $p k = a k + ib k$ с $нечетным$ и положительным, а $b$ четным,
или остаток от евклидова деления $p k$ на $2 + 2 i$ равен 1 (это изначальный выбор Гаусса ^[5] ).

Преимущество второго выбора заключается в том, что выбранные ассоциированные элементы хорошо ведут себя при произведениях для гауссовых целых чисел нечетной нормы. С другой стороны, выбранные ассоциированные элементы для действительных гауссовых простых чисел являются отрицательными целыми числами. Например, факторизация 231 в целых числах и при первом выборе ассоциированных элементов равна 3 × 7 × 11 , тогда как при втором выборе она равна (–1) × (–3) × (–7) × (–11) .

Гауссовы рациональные числа

Поле гауссовых рациональных чисел — это поле дробей кольца гауссовых целых чисел. Оно состоит из комплексных чисел, действительная и мнимая части которых являются рациональными .

Кольцо гауссовых целых чисел представляет собой интегральное замыкание целых чисел в гауссовых рациональных числах.

Это означает, что гауссовы целые числа являются квадратичными целыми числами и что гауссово рациональное число является гауссовым целым числом тогда и только тогда, когда оно является решением уравнения

x^{2}+cx+d=0,

с целыми числами $c$ и $d$ . Фактически $a + bi$ является решением уравнения

x^{2}-2ax+a^{2}+b^{2},

и это уравнение имеет целые коэффициенты тогда и только тогда, когда $a$ и $b$ оба являются целыми числами.

Наибольший общий делитель

Как и для любой уникальной области факторизации , наибольший общий делитель (НОД) двух гауссовых целых чисел $a, b$ — это гауссово целое число $d$ , которое является общим делителем $a$ и $b$ , и которое имеет все общие делители $a$ и $b$ в качестве делителя. То есть (где $|$ обозначает отношение делимости ),

$г | а$ и $г | б$ , и
$c | a$ и $c | b$ подразумевают $c | d$ .

Таким образом, наибольшее подразумевается относительно отношения делимости, а не для упорядочения кольца (для целых чисел оба значения наибольшего совпадают).

Более технически, наибольший общий делитель $a$ и $b$ является генератором идеала, порожденного a $и$ b $($ эта характеристика верна для областей главных идеалов , но, в общем случае, не для областей уникальной факторизации).

Наибольший общий делитель двух гауссовых целых чисел не является уникальным, но определяется с точностью до умножения на единицу . То есть, если задан наибольший общий делитель $d$ чисел $a$ и $b$ , наибольшими общими делителями чисел $a$ и $b$ являются $d, - d, id$ и $- id$ .

Существует несколько способов вычисления наибольшего общего делителя двух гауссовых целых чисел $a$ и $b$ . Когда известны простые множители $a$ и $b$ ,

a=i^{k}\prod _{m}{p_{m}}^{\nu _{m}},\quad b=i^{n}\prod _{m}{p_{m}}^{\mu _{m}},

где простые числа $p m$ попарно не связаны, а показатели $μ m$ не связаны, наибольший общий делитель равен

\prod _{m}{p_{m}}^{\lambda _{m}},

\lambda _{m} =\min(\nu _{m},\mu _{m}).

К сожалению, за исключением простых случаев, разложение на простые множители трудно вычислить, и алгоритм Евклида приводит к гораздо более простому (и быстрому) вычислению. Этот алгоритм состоит из замены входных данных $(a, b)$ на $(b, r)$ , где $r$ — остаток от евклидова деления $a$ на $b$ , и повторения этой операции до получения нулевого остатка, то есть пары $(d, 0)$ . Этот процесс завершается, потому что на каждом шаге норма второго гауссовского целого числа уменьшается. Полученное $d$ является наибольшим общим делителем, потому что (на каждом шаге) $b$ и $r = a - bq$ имеют те же делители, что и $a$ и $b$ , и, таким образом, тот же самый наибольший общий делитель.

Этот метод вычисления работает всегда, но не так прост, как для целых чисел, потому что евклидово деление сложнее. Поэтому для рукописных вычислений часто предпочитают третий метод. Он состоит в том, чтобы заметить, что норма $N (d)$ наибольшего общего делителя $a$ и $b$ является общим делителем $N (a)$ , $N (b)$ и $N (a + b)$ . Когда наибольший общий делитель $D$ этих трех целых чисел имеет несколько множителей, то легко проверить на общий делитель все гауссовы целые числа с нормой, делящей $D$ .

Например, если $a = 5 + 3 i$ , а $b = 2 - 8 i$ , то $N (a) = 34$ , $N (b) = 68$ и $N (a + b) = 74$ . Поскольку наибольший общий делитель трех норм равен 2 , наибольший общий делитель $a$ и $b$ имеет норму 1 или 2 . Поскольку гауссово целое число нормы 2 необходимо связано с $1 + i$ , и поскольку $1 + i$ делит $a$ и $b$ , то наибольший общий делитель равен $1 + i$ .

Если заменить $b на его сопряженное число$ $b = 2 + 8 i$ , то наибольший общий делитель трех норм равен 34, норме $a$ , таким образом, можно предположить, что наибольший общий делитель равен $a$ , то есть, что $a | b$ . Фактически, имеем $2 + 8 i = (5 + 3 i)(1 + i)$ .

Сравнения и классы остатков

Для заданного гауссова целого числа $z 0$ , называемого модулем , два гауссова целых числа $z 1, z 2$ сравнимы по модулю $z 0$ , если их разность кратна $z 0$ , то есть если существует гауссово целое число $q$ такое, что $z 1 - z 2 = qz 0$ . Другими словами, два гауссова целых числа сравнимы по модулю $z 0$ , если их разность принадлежит идеалу , порожденному $z 0$ . Это обозначается как $z 1 \equiv z 2 (mod z 0)$ .

Сравнимость по модулю $z 0$ — это отношение эквивалентности (также называемое отношением конгруэнтности ), которое определяет разбиение гауссовых целых чисел на классы эквивалентности , называемые здесь классами конгруэнтности или классами вычетов . Множество классов вычетов обычно обозначается $Z [i]/ z 0 Z [i]$ , или $Z [i]/ ⟨ z 0 ⟩$ , или просто $Z [i]/ z 0$ .

Остаточный класс гауссовского целого числа $a$ — это множество

{\bar {a}}:=\left\{z\in \mathbf {Z} [i]\mid z\equiv a{\pmod {z_{0}}}\right\}

всех гауссовых целых чисел, которые конгруэнтны $a$ . Отсюда следует, что $a = b$ тогда и только тогда, когда $a \equiv b (mod z 0)$ .

Сложение и умножение совместимы с конгруэнциями. Это означает, что $a 1 \equiv b 1 (mod z 0)$ и $a 2 \equiv b 2 (mod z 0)$ подразумевают $a 1 + a 2 \equiv b 1 + b 2 (mod z 0)$ и $a 1 a 2 \equiv b 1 b 2 (mod z 0)$ . Это определяет хорошо определенные операции (не зависящие от выбора представителей) на классах остатков:

{\bar {a}}+{\bar {b}}:={\overline {a+b}}\quad {\text{and}}\quad {\bar {a}}\cdot {\bar {b}}:={\overline {ab}}.

С помощью этих операций классы вычетов образуют коммутативное кольцо — фактор-кольцо целых гауссовых чисел по идеалу, порожденному $z 0$ , которое также традиционно называют кольцом классов вычетов по модулю $z 0$ (подробнее см. в разделе Фактор-кольцо ).

Примеры

Существует ровно два класса вычетов для модуля $1 + i$ , а именно $0 = {0, \pm2, \pm4,\dots,\pm1 \pm i, \pm3 \pm i,\dots}$ (все кратные $1 + i$ ), и $1 = {\pm1, \pm3, \pm5,\dots, \pm i, \pm2 \pm i,\dots}$ , которые образуют шахматный узор на комплексной плоскости. Эти два класса образуют, таким образом, кольцо с двумя элементами, которое, по сути, является полем , единственным (с точностью до изоморфизма) полем с двумя элементами, и, таким образом, может быть отождествлено с целыми числами по модулю 2 . Эти два класса можно рассматривать как обобщение разбиения целых чисел на четные и нечетные целые числа. Таким образом, можно говорить о четных и нечетных гауссовых целых числах (Гаусс разделил четные гауссовы целые числа на четные , то есть делящиеся на 2, и получетные ).
Для модуля 2 существует четыре класса вычетов, а именно $0, 1, i, 1 + i$ . Они образуют кольцо с четырьмя элементами, в котором $x = - x$ для каждого $x$ . Таким образом, это кольцо не изоморфно кольцу целых чисел по модулю 4, другому кольцу с четырьмя элементами. Можно иметь $1 + i 2 = 0$ , и, таким образом, это кольцо не является ни конечным полем с четырьмя элементами, ни прямым произведением двух копий кольца целых чисел по модулю 2.
Для модуля $2 + 2i = (i - 1) 3$ существует восемь классов вычетов, а именно $0, \pm1, \pm i, 1 \pm i, 2$ , из которых четыре содержат только четные гауссовы целые числа, а четыре содержат только нечетные гауссовы целые числа.

Описание классов остатков

Все 13 классов вычетов с их минимальными вычетами (синие точки) в квадрате $Q 00$ (светло-зеленый фон) для модуля $z 0 = 3 + 2 i$ . Один класс вычетов с $z = 2 - 4 i \equiv - i (mod z 0)$ выделен желтыми/оранжевыми точками.

При заданном модуле $z 0$ все элементы класса остатков имеют одинаковый остаток от евклидова деления на $z 0$ , при условии использования деления с уникальным частным и остатком, которое описано выше. Таким образом, перечисление классов остатков эквивалентно перечислению возможных остатков. Это можно сделать геометрически следующим образом.

На комплексной плоскости можно рассмотреть квадратную сетку , квадраты которой ограничены двумя линиями

{\begin{aligned}V_{s}&=\left\{\left.z_{0}\left(s-{\tfrac {1}{2}}+ix\right)\right\vert x\in \mathbf {R} \right\}\quad {\text{and}}\\H_{t}&=\left\{\left.z_{0}\left(x+i\left(t-{\tfrac {1}{2}}\right)\right)\right\vert x\in \mathbf {R} \right\},\end{aligned}}

с целыми числами $s$ и $t$ (синие линии на рисунке). Они делят плоскость на полуоткрытые квадраты (где $m$ и $n$ — целые числа)

Q_{mn}=\left\{(s+it)z_{0}\left\vert s\in \left[m-{\tfrac {1}{2}},m+{\tfrac {1}{2}}\right),t\in \left[n-{\tfrac {1}{2}},n+{\tfrac {1}{2}}\right)\right.\right\}.

Полуоткрытые интервалы, которые встречаются в определении $Q mn,$ были выбраны таким образом, чтобы каждое комплексное число принадлежало ровно одному квадрату; то есть квадраты $Q mn$ образуют разбиение комплексной плоскости. Можно

Q_{mn}=(m+in)z_{0}+Q_{00}=\left\{(m+in)z_{0}+z\mid z\in Q_{00}\right\}.

Это означает, что каждое гауссово целое число сравнимо по модулю $z 0$ с уникальным гауссовым целым числом в $Q 00$ (зеленый квадрат на рисунке), который является его остатком от деления на $z 0$ . Другими словами, каждый класс остатков содержит ровно один элемент в $Q 00$ .

Гауссовы целые числа в $Q 00$ (или на его границе ) иногда называются минимальными остатками , поскольку их норма не больше нормы любого другого гауссовского целого числа в том же классе остатков (Гаусс называл их абсолютно наименьшими остатками ).

Из этого можно вывести с помощью геометрических соображений, что число классов вычетов по модулю целого числа Гаусса $z 0 = a + bi$ равно его норме $N (z 0) = a 2 + b 2$ (доказательство см. ниже; аналогично, для целых чисел число классов вычетов по модулю $n$ равно его абсолютному значению $| n |$ ).

Доказательство

Соотношение $Q mn = (m + in) z 0 + Q 00$ означает, что все $Q mn$ получены из $Q 00$ путем его преобразования в гауссово целое число. Это подразумевает, что все $Q mn$ имеют одинаковую площадь $N = N (z 0)$ и содержат одинаковое количество $n g$ гауссовых целых чисел.

В общем случае число точек сетки (здесь гауссовы целые числа) в произвольном квадрате с площадью $A$ равно $A + Θ (\sqrt A)$ (см. Big theta для обозначения). Если рассмотреть большой квадрат, состоящий из $k \times k$ квадратов $Q mn$ , то он содержит $k 2 N + O (k \sqrt N)$ точек сетки. Из этого следует $k 2 n g = k 2 N + Θ (k \sqrt N)$ , и, таким образом, $n g = N + Θ (⁠ \sqrt Н / к ⁠)$ после деления на $k 2.$ Взяв предел, когда $k$ стремится к бесконечности, получаем $n g = N = N (z 0)$ .

Поля остаточного класса

Кольцо классов вычетов по модулю гауссовского целого числа $z 0$ является полем тогда и только тогда, когда — гауссово простое число. $z_{0}$

Если $z 0$ является разложенным простым числом или разветвленным простым числом $1 + i$ (то есть, если его норма $N (z 0)$ является простым числом, которое равно либо 2, либо простому числу, сравнимому с 1 по модулю 4), то поле класса вычетов имеет простое число элементов (то есть $N (z 0)$ ). Таким образом, оно изоморфно полю целых чисел по модулю $N (z 0)$ .

Если, с другой стороны, $z 0$ — инертное простое число (то есть $N (z 0) = p 2$ — квадрат простого числа, сравнимый с 3 по модулю 4), то поле вычетных классов имеет $p 2$ элементов и является расширением степени 2 (единственным с точностью до изоморфизма) простого поля с $p$ элементами (целыми числами по модулю $p$ ).

Группа примитивных вычетов и функция Эйлера

Многие теоремы (и их доказательства) для модулей целых чисел можно напрямую перенести на модули гауссовых целых чисел, если заменить абсолютное значение модуля нормой. Это особенно справедливо для примитивной группы классов вычетов (также называемой мультипликативной группой целых чисел по модулю $n$ ) и функции тотиента Эйлера . Примитивная группа классов вычетов модуля $z$ определяется как подмножество ее классов вычетов, которое содержит все классы вычетов $a ,$ которые взаимно просты с $z$ , т.е. $(a, z) = 1$ . Очевидно, что эта система образует мультипликативную группу . Число ее элементов будет обозначаться как $ϕ (z)$ (аналогично функции тотиента Эйлера $φ (n)$ для целых чисел $n$ ).

Для гауссовых простых чисел немедленно следует, что $ϕ (p) = | p | 2 - 1$ , а для произвольных составных гауссовых целых чисел

z=i^{k}\prod _{m}{p_{m}}^{\nu _{m}}

Формулу произведения Эйлера можно вывести как

\phi (z)=\prod _{m\,(\nu _{m}>0)}{\bigl |}{p_{m}}^{\nu _{m}}{\bigr |}^{2}\left(1-{\frac {1}{|p_{m}|{}^{2}}}\right)=|z|^{2}\prod _{p_{m}|z}\left(1-{\frac {1}{|p_{m}|{}^{2}}}\right)

где произведение строится по всем простым делителям $p m$ числа $z$ (при $ν m > 0$ ). Также важная теорема Эйлера может быть напрямую перенесена:

Для всех

a

(a, z) = 1

справедливо, что

a ϕ (z) \equiv 1 (mod z)

Историческая справка

Кольцо гауссовых целых чисел было введено Карлом Фридрихом Гауссом в его второй монографии о квартикальной взаимности (1832). ^[6] Теорема квадратичной взаимности (которую он впервые доказал в 1796 году) связывает разрешимость сравнения $x 2 \equiv q (mod p)$ с разрешимостью сравнения $x 2 \equiv p (mod q)$ . Аналогично, кубическая взаимность связывает разрешимость сравнения $x 3 \equiv q (mod p)$ с разрешимостью сравнения $x 3 \equiv p (mod q)$ , а биквадратичная (или квартикальная) взаимность является соотношением между $x 4 \equiv q (mod p)$ и $x 4 \equiv p (mod q)$ . Гаусс обнаружил, что закон биквадратичной взаимности и его дополнения легче сформулировать и доказать как утверждения о «целых комплексных числах» (т. е. целых гауссовых числах), чем как утверждения об обычных целых числах (т. е. целых числах).

В сноске он отмечает, что целые числа Эйзенштейна являются естественной областью для формулировки и доказательства результатов кубической взаимности , и указывает, что подобные расширения целых чисел являются подходящими областями для изучения высших законов взаимности.

В этой статье не только были введены гауссовы целые числа и доказано, что они являются уникальной областью факторизации, но также были введены термины «норма», «единица», «первичный» и «ассоциированный», которые теперь являются стандартными в алгебраической теории чисел.

Нерешенные проблемы

Распределение малых гауссовых простых чисел в комплексной плоскости

Большинство нерешенных проблем связано с распределением гауссовых простых чисел на плоскости.

Задача Гаусса о круге не имеет дела с гауссовыми целыми числами как таковыми, а вместо этого запрашивает количество точек решетки внутри круга заданного радиуса с центром в начале координат. Это эквивалентно определению количества гауссовых целых чисел с нормой, меньшей заданного значения.

Существуют также гипотезы и нерешенные проблемы о гауссовых простых числах. Две из них:

Действительная и мнимая оси имеют бесконечное множество гауссовых простых чисел 3, 7, 11, 19, ... и их ассоциированных. Существуют ли другие линии, которые имеют бесконечно много гауссовых простых чисел на них? В частности, существует ли бесконечно много гауссовых простых чисел вида $1 + ki$ ? ^[7]
Можно ли дойти до бесконечности, используя гауссовы простые числа в качестве ступенек и делая шаги равномерно ограниченной длины? Это известно как проблема гауссовского рва ; она была поставлена в 1962 году Бэзилом Гордоном и остается нерешенной. ^[8]^[9]

Смотрите также

Алгебраическое целое число
Циклотомическое поле
Целое число Эйзенштейна
Эйзенштейн премьер
кватернион Гурвица
Доказательства теоремы Ферма о суммах двух квадратов
Доказательства квадратичной взаимности
Квадратное целое число
Расщепление простых идеалов в расширениях Галуа описывает структуру простых идеалов в гауссовых целых числах.
Таблица гауссовых целочисленных факторизаций

Примечания

^ ab Fraleigh (1976, стр. 286)
^ Фрейли (1976, стр. 289)
^ Фрейли (1976, стр. 288)
^ Фрейли (1976, стр. 287)
^ Гаусс (1831, стр. 546)
^ Кляйнер (1998)
^ Рибенбойм, Гл. III.4.D Гл. 6.II, Гл. 6.IV (гипотеза Харди и Литтлвуда E и F)
^ Гетнер, Эллен; Вагон, Стэн ; Вик, Брайан (1998). «Прогулка по гауссовым простым числам». The American Mathematical Monthly . 105 (4): 327–337. doi :10.2307/2589708. JSTOR 2589708. MR 1614871. Zbl 0946.11002.
^ Гай, Ричард К. (2004). Нерешенные проблемы теории чисел (3-е изд.). Springer-Verlag . С. 55–57. ISBN 978-0-387-20860-2. Збл 1058.11001.

Ссылки

Гаусс, CF (1831), "Theoria residuorum biquadraticorum. Commentatio secunda.", Comm. Соц. Рег. наук. Геттинген , 7 : 89–148.; перепечатано в Werke, Georg Olms Verlag, Хильдесхайм, 1973, стр. 93–148. Немецкий перевод этой статьи доступен в Интернете по адресу ″H. Мазер (ред.): Арифметическая арифметика Карла Фридриха Гаусса über höhere Arithmetik. Шпрингер, Берлин, 1889 г., стр. 534».
Фрейли, Джон Б. (1976), Первый курс абстрактной алгебры (2-е изд.), Чтение: Addison-Wesley , ISBN 0-201-01984-1
Кляйнер, Израиль (1998). «От чисел к кольцам: ранняя история теории колец». Elem. Math. 53 (1): 18–35. doi : 10.1007/s000170050029 . Zbl 0908.16001.
Рибенбойм, Пауло (1996). Новая книга записей простых чисел (3-е изд.). Нью-Йорк: Springer. ISBN 0-387-94457-5. Збл 0856.11001.
Генри Г. Бейкер (1993). «Комплексные гауссовские целые числа для «гауссовой графики»". Уведомления ACM SIGPLAN . 28 (11): 22–27. doi :10.1145/165564.165571. S2CID 8083226.

Внешние ссылки

Текст сборника ИМО по квадратичным расширениям и гауссовым целым числам в решении задач
Кит Конрад, Гауссовы целые числа.