Генерация высоких гармоник

Лазерный научный процесс

Генерация высоких гармоник ( ГВГ ) — это нелинейный процесс, в ходе которого мишень (газ, плазма, твердый или жидкий образец) освещается интенсивным лазерным импульсом. При таких условиях образец будет излучать высокие гармоники луча генерации (выше пятой гармоники). В связи с когерентным характером процесса генерация высоких гармоник является предпосылкой аттосекундной физики .

Генерация возмущенных гармоник

Генерация пертурбационной гармоники — это процесс, при котором лазерный свет с частотой ω и энергией фотона ħω может использоваться для генерации новых частот света. Новые сгенерированные частоты являются целыми кратными nω исходной частоты света. Этот процесс был впервые обнаружен в 1961 году Франкеном и др. ^[1] с использованием рубинового лазера с кристаллическим кварцем в качестве нелинейной среды .

Генерация гармоник в диэлектрических твердых телах хорошо изучена и широко используется в современной лазерной физике (см. генерация второй гармоники ). В 1967 году Нью и др. наблюдали первую генерацию третьей гармоники в газе. ^[2] В одноатомных газах возможно создание только нечетных гармоник по причинам симметрии. Генерация гармоник в пертурбативном (слабом поле) режиме характеризуется быстро уменьшающейся эффективностью с увеличением порядка гармоники. ^[3] Такое поведение можно понять, рассмотрев атом, поглощающий n фотонов , а затем испускающий один фотон высокой энергии. Вероятность поглощения n фотонов уменьшается с увеличением n , что объясняет быстрое уменьшение начальной интенсивности гармоник.

Разработка

Спектр неонового источника ГВГ, возбуждаемого титан-сапфировым лазером

Первая генерация высоких гармоник наблюдалась в 1977 году при взаимодействии интенсивных импульсов CO2 _- лазера с плазмой, генерируемой из твердых мишеней. ^[4] ГВГ в газах, гораздо более распространенная в настоящее время в применении, была впервые обнаружена Макферсоном и коллегами в 1987 году, ^[5] а затем Ферреем и др. в 1988 году, ^[6] с удивительными результатами: было обнаружено, что высокие гармоники уменьшаются в интенсивности в низких порядках, как и ожидалось, но затем наблюдалось образование плато, при этом интенсивность гармоник оставалась приблизительно постоянной на протяжении многих порядков. ^[7] Были измерены гармоники плато, охватывающие сотни эВ, которые простираются в режим мягкого рентгеновского излучения . ^[8] Это плато резко заканчивается в положении, называемом отсечкой высоких гармоник.

Характеристики

Высокие гармоники обладают рядом интересных свойств. Они представляют собой настраиваемый настольный источник XUV /мягкого рентгеновского излучения, синхронизированный с ведущим лазером и производимый с той же частотой повторения. Отсечка гармоник изменяется линейно с ростом интенсивности лазера до интенсивности насыщения, _на которой прекращается генерация гармоник. ^[9] Интенсивность насыщения можно увеличить, изменив атомные виды на более легкие благородные газы , но они имеют более низкую эффективность преобразования, поэтому необходимо найти баланс в зависимости от требуемых энергий фотонов.

Генерация высоких гармоник сильно зависит от поля ведущего лазера, и в результате гармоники имеют схожие свойства временной и пространственной когерентности. ^[10] Высокие гармоники часто генерируются с длительностью импульса короче, чем у ведущего лазера. ^[11] Это происходит из-за нелинейности процесса генерации, фазового согласования и ионизации . Часто гармоники производятся только в очень маленьком временном окне, когда выполняется условие фазового согласования. Истощение генерирующей среды из-за ионизации также означает, что генерация гармоник в основном ограничивается передним фронтом импульса возбуждения. ^[12]

Высокие гармоники излучаются коллинеарно с ведущим лазером и могут иметь очень жесткое угловое ограничение, иногда с меньшей расходимостью, чем у основного поля, и близкими к гауссовым профилям пучка. ^[13]

Полуклассический подход

Максимальная энергия фотона, производимая при генерации высокой гармоники, определяется отсечкой гармонического плато. Это можно рассчитать классически , изучив максимальную энергию, которую ионизированный электрон может получить в электрическом поле лазера. Энергия отсечки определяется как: ^[14]

${\displaystyle E_{\mathrm {max} }=I_{p}+3.17\ U_{p}}$

где U _p — пондеромоторная энергия лазерного поля, а I _p — потенциал ионизации .

Эта энергия отсечки выводится из полуклассического расчета, часто называемого трехшаговой моделью. Электрон изначально рассматривается квантово-механически, поскольку он туннелирует ионизируется из родительского атома, но его последующая динамика рассматривается классически. Предполагается, что электрон рождается в вакууме с нулевой начальной скоростью и впоследствии ускоряется электрическим полем лазерного луча .

Трехэтапная модель

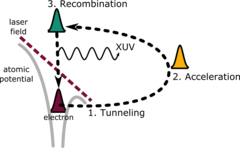
Через половину оптического цикла после ионизации электрон изменит направление, поскольку электрическое поле изменит знак, и ускорится обратно к родительскому ядру. После возвращения к родительскому ядру он может испускать излучение, подобное тормозному , во время процесса рекомбинации с атомом, когда он возвращается в свое основное состояние . Это описание стало известно как реколлиссионная модель генерации высоких гармоник. ^[15]

Энергия возврата электрона (сплошная синяя кривая) и время движения (синяя пунктирная кривая) как функция времени возврата

Поскольку частота испускаемого излучения зависит как от кинетической энергии, так и от потенциала ионизации, различные частоты испускаются в разное время рекомбинации (т. е. испускаемый импульс чирпируется ) . Более того, для каждой частоты существует два соответствующих времени рекомбинации. Мы называем эти две траектории короткой траекторией (которая испускается первой) и длинной траекторией.

В полуклассической картине HHG будет происходить только в том случае, если поле ведущего лазера линейно поляризовано. Эллиптичность лазерного луча заставляет возвращающийся электрон промахиваться мимо родительского ядра. Квантово-механически перекрытие волнового пакета возвращающегося электрона с ядерным волновым пакетом уменьшается. Это наблюдалось экспериментально, где интенсивность гармоник быстро уменьшается с увеличением эллиптичности. ^[16] Другим эффектом, ограничивающим интенсивность ведущего лазера, является сила Лоренца . При интенсивностях выше 10 ¹⁶ Вт·см ⁻² магнитная составляющая лазерного импульса, которая игнорируется в оптике слабого поля, может стать достаточно сильной, чтобы отклонить возвращающийся электрон. Это заставит его «промахнуться» мимо родительского ядра и, следовательно, предотвратить HHG.

Фазовое согласование

Как и в каждом нелинейном процессе, фазовое согласование играет важную роль в генерации высоких гармоник в газовой фазе. В геометрии свободной фокусировки четырьмя причинами несоответствия волнового вектора являются: нейтральная дисперсия, плазменная дисперсия, фаза Гуи и дипольная фаза. ^{[17] [18]}

Нейтральная дисперсия вызвана атомами, в то время как плазменная дисперсия вызвана ионами, и эти две имеют противоположные знаки. Фаза Гуи обусловлена ​​скачком фазы волнового фронта вблизи фокуса и изменяется вдоль него. Наконец, дипольная фаза возникает из-за атомного отклика в процессе HHG. ^[19] При использовании геометрии газовой струи оптимальные условия для генерации высоких гармоник, испускаемых с коротких траекторий, достигаются, когда генерирующий газ находится после фокуса, в то время как генерация высоких гармоник с длинной траектории может быть получена вне оси, когда генерирующий газ находится перед фокусом. ^[20]

Кроме того, реализация геометрии свободной фокусировки для ведущего поля позволяет большему числу излучателей и фотонов участвовать в процессе генерации и, таким образом, повышать выход гармоник. ^[21] При использовании геометрии газовой струи фокусировка лазера в диск Маха может повысить эффективность генерации гармоник. ^[22]

В более общем смысле, в рентгеновской области спектра материалы имеют показатель преломления, очень близкий к 1. Чтобы уравновесить фазовое рассогласование, нам необходимо найти такие параметры в многомерном пространстве, которые фактически сделают объединенный показатель преломления на длине волны ведущего лазера близким к 1. ${\displaystyle \Delta k=k_{q}-qk_{L}}$

Для достижения уровней интенсивности, которые могут исказить потенциал связи атома, необходимо сфокусировать управляющий лазерный луч. Это вводит дисперсионные члены, влияющие на фазовое рассогласование, в зависимости от конкретной геометрии (например, распространение плоской волны, свободная фокусировка, волновод с полым сердечником и т. д.). Кроме того, в процессе генерации высоких гармоник электроны ускоряются, и некоторые из них возвращаются к своему родительскому иону, что приводит к рентгеновским вспышкам. Однако большинство этих электронов не возвращаются, а вместо этого вносят вклад в дисперсию для совместно распространяющихся волн. Возвращающиеся электроны переносят фазу из-за таких процессов, как ионизация, рекомбинация и распространение. Кроме того, ионизированные атомы могут влиять на показатель преломления среды, обеспечивая еще один источник дисперсии.

Фазовое рассогласование (> 0 фазовая скорость лазера больше, чем у рентгеновских лучей) можно представить как:

${\displaystyle \Delta k=k_{q}-qk_{L}=\underbrace {\Delta k_{\mathrm {neutrals} }} _{<0}+\underbrace {\Delta k_{\mathrm {ions} }} _{<0}+\underbrace {\Delta k_{\mathrm {electrons} }} _{>0}+\underbrace {\Delta k_{\mathrm {geometry} }} _{>0}+\underbrace {\Delta k_{\mathrm {intrinsic} }} _{>\;\!0}+\cdots }$

где — вклад нейтральных атомов, — вклад ионов (при ионизации нейтралов этот член может быть все еще достаточно большим в УФ-диапазоне ^[23] ), — плазменный вклад, — геометрия свободной фокусировки, плоская волна или волноводная геометрия, — фаза, накопленная электроном за время, проведенное им вдали от атома, и т. д. Каждый член имеет определенный знак, позволяющий компенсировать рассогласование в определенное время и на определенной частоте. ${\displaystyle \Delta k_{\mathrm {neutrals} }}$ ${\displaystyle \Delta k_{\mathrm {ions} }}$ ${\displaystyle \Delta k_{\mathrm {electrons} }}$ ${\displaystyle \Delta k_{\mathrm {geometry} }}$ ${\displaystyle \Delta k_{\mathrm {intrinsic} }}$

Вклад электронов масштабируется квадратично с длиной волны: , в то время как вклад атомов масштабируется обратно пропорционально длине волны: . Таким образом, на длинных ИК-волнах член довольно велик на электрон, в то время как член довольно мал и близок к единице. Для согласования фаз процесса HHG требуются очень высокие давления и низкие уровни ионизации, что дает большое количество излучателей. ^[24] В противоположном УФ-спектральном диапазоне член велик из-за близко расположенных УФ-резонансов, и, кроме того, член мал. Для согласования фаз процесса необходимы низкие давления. Более того, в УФ-диапазоне могут быть допущены очень высокие уровни ионизации (намного больше 100%). Это дает масштабируемость энергии фотонов HHG с интенсивностью управляющего УФ-лазера. ^[23] Геометрия плоской волны или геометрия со слабой фокусировкой обеспечивает высококоллинеарное согласование фаз и максимальное извлечение потока на управляющих длинах волн, где член мал. Генерация гармоник высокого порядка в волноводе позволяет распространять волны с характеристиками, близкими к характеристикам распространения плоской волны. ^[25] Такие геометрии дают преимущества, особенно рентгеновские спектры, генерируемые ИК-лучами, где для оптимального извлечения мощности требуются большие объемы взаимодействия. В таких геометриях были получены спектры, простирающиеся до 1,6 кэВ. ^[24] Для высоких гармоник, возбуждаемых в УФ-ВИД, волноводный член мал, а картина фазового согласования напоминает геометрию плоской волны. В таких геометриях были получены гармоники с узкой полосой пропускания, простирающиеся до края углерода (300 эВ). ^[23] ${\displaystyle \Delta n_{\mathrm {electrons} }\sim -\lambda ^{2}}$ ${\displaystyle \Delta n_{\mathrm {atoms} }\sim 1/\lambda ^{2}}$ ${\displaystyle \left|\Delta n_{\mathrm {electrons} }\right|}$ ${\displaystyle \Delta n_{\mathrm {atoms} }}$ ${\displaystyle \Delta n_{\mathrm {atoms} }}$ ${\displaystyle \left|\Delta n_{\mathrm {electrons} }\right|}$ ${\displaystyle {\vec {v}}\times {\vec {B}}}$

Смотрите также

• Аттосекундная физика
• Нелинейная оптика
• Фотоионизация
• Резонансная генерация высоких гармоник из плазменных факелов, полученных путем лазерной абляции

Ссылки

1. PA Franken, AE Hill, CW Peters и G. Weinreich, Phys. Rev. Lett. 7, 118 (1961).
2. New, GHC; Ward, JF (1967). «Генерация оптической третьей гармоники в газах». Phys. Rev. Lett . 19 (10): 556–559. Bibcode : 1967PhRvL..19..556N. doi : 10.1103/physrevlett.19.556.
3. Дж. Вильденауэр, Журнал прикладной физики 62, 41 (1987).
4. Бернетт, NH; и др. (1977). «Генерация гармоник при взаимодействии лазера CO2 с мишенью». Appl. Phys. Lett . 31 (3): 172–174. Bibcode :1977ApPhL..31..172B. doi :10.1063/1.89628.
5. Макферсон, А.; и др. (1987). "Исследования многофотонного производства вакуумно-ультрафиолетового излучения в инертных газах". JOSA B . 4 (4): 595. Bibcode :1987JOSAB...4..595M. doi :10.1364/JOSAB.4.000595.
6. Феррей, М.; и др. (1988). "Многогармоническое преобразование излучения 1064 нм в инертных газах". Журнал физики B: атомная, молекулярная и оптическая физика . 21 (3): L31. Bibcode : 1988JPhB...21L..31F. doi : 10.1088/0953-4075/21/3/001. S2CID  250827054.
7. Ли, XF; Л'Юлье, А.; Феррей, М.; Ломпре, ЛА; Мейнфрей, Г. (1989). «Генерация множественных гармоник в инертных газах при высокой интенсивности лазера». Physical Review A. 39 ( 11): 5751–5761. Bibcode : 1989PhRvA..39.5751L. doi : 10.1103/physreva.39.5751. PMID  9901157.
8. Seres, J.; et al. (2005). "Лазерная технология: Источник когерентных килоэлектронвольтных рентгеновских лучей". Nature . 433 (7026): 596. Bibcode :2005Natur.433..596S. doi : 10.1038/433596a . PMID  15703738. S2CID  4425428.
9. Brabec, T.; Krausz, F. (2000). «Интенсивные лазерные поля с несколькими циклами: Границы нелинейной оптики». Reviews of Modern Physics . 72 (2): 545–591. Bibcode : 2000RvMP...72..545B. doi : 10.1103/revmodphys.72.545.
10. L'Huillier, A.; Schafer, KJ; Kulander, KC (1991). «Теоретические аспекты генерации гармоник интенсивного поля». Journal of Physics B: Atomic, Molecular and Optical Physics . 24 (15): 3315–3341. Bibcode :1991JPhB...24.3315L. doi :10.1088/0953-4075/24/15/004. S2CID  250751106.
11. Полосы 43-аттосекундных импульсов мягкого рентгеновского излучения, генерируемые пассивно стабильным CEP-источником в среднем инфракрасном диапазоне, https://doi.org/10.1364/OE.25.027506
12. Schafer, KJ; Kulander, KC (1997). "High Harmonic Generation from Ultrafast Pump Lasers". Physical Review Letters . 78 (4): 638–641. Bibcode : 1997PhRvL..78..638S. doi : 10.1103/physrevlett.78.638.
13. Tisch, JWG; et al. (1994). "Генерация гармоник высокого порядка с угловым разрешением в гелии". Physical Review A. 49 ( 1): R28–R31. Bibcode : 1994PhRvA..49...28T. doi : 10.1103/physreva.49.r28. PMID  9910285.
14. Krause, Jeffrey L.; Schafer, Kenneth J.; Kulander, Kenneth C. (1992). «Генерация гармоник высокого порядка из атомов и ионов в режиме высокой интенсивности». Physical Review Letters . 68 (24): 3535–3538. Bibcode :1992PhRvL..68.3535K. doi :10.1103/PhysRevLett.68.3535. PMID  10045729.
15. Corkum, PB (1993). «Плазменная перспектива многофотонной ионизации в сильном поле». Physical Review Letters . 71 (13): 1994–1997. Bibcode : 1993PhRvL..71.1994C. doi : 10.1103/physrevlett.71.1994. PMID  10054556. S2CID  29947935.
16. Дитрих, П.; Бернетт, Н. Х.; Иванов, М.; Коркум, П. Б. (1994). «Высокогармоническая генерация и коррелированная двухэлектронная многофотонная ионизация с эллиптически поляризованным светом». Physical Review A. 50 ( 5): R3585–R3588. Bibcode : 1994PhRvA..50.3585D. doi : 10.1103/physreva.50.r3585. PMID  9911439.
17. Altucci, C.; Starczewski, T.; Mevel, E.; Wahlström, C.-G.; Carré, B.; L'Huillier, A. (1996). «Влияние атомной плотности на генерацию гармоник высокого порядка». J. Opt. Soc. Am. B . 13 (1): 148–156. Bibcode :1996JOSAB..13..148A. doi :10.1364/JOSAB.13.000148.
18. Паскаль, Сальер; Люлье, Энн; Левенштейн, Мачей (1995). «Управление когерентностью гармоник высокого порядка» (PDF) . Physical Review Letters . 74 (19): 3776–3779. Bibcode : 1995PhRvL..74.3776S. doi : 10.1103/physrevlett.74.3776. PMID  10058294. S2CID  35091499.
19. Левенштейн, Мачей; Сальер, Паскаль; Люлье, Энн (1995). «Фаза атомной поляризации при генерации гармоник высокого порядка». Physical Review A. 52 ( 6): 4747–4754. Bibcode : 1995PhRvA..52.4747L. doi : 10.1103/physreva.52.4747. PMID  9912816.
20. Балку, Филипп; Сальер, Паскаль; Люлье, Энн; Левенштейн, Мачей (1997). «Обобщенные условия фазового согласования для высоких гармоник: роль сил градиента поля». Physical Review A. 55 ( 4): 3204–3210. Bibcode : 1997PhRvA..55.3204B. doi : 10.1103/PhysRevA.55.3204.
21. Takahashi, E.; Nabekawa, Y.; Midorikawa, K. (2002). «Генерация 10-uj когерентного экстремально-ультрафиолетового света с использованием гармоник высокого порядка». Optics Letters . 27 (21): 1920–1922. Bibcode : 2002OptL...27.1920T. doi : 10.1364/OL.27.001920. PMID  18033402.
22. Грант-Джейкоб, Джеймс; Миллс, Бен; Бутчер, Том; Чепмен, Ричард; Броклсби, Уильям; Фрей, Джереми (2011). «Влияние структуры газовой струи на генерацию высоких гармоник» (PDF) . Optics Express . 19 (10): 9801–9806. Bibcode :2011OExpr..19.9801G. doi : 10.1364/OE.19.009801 . PMID  21643236.
23. Popmintchev, D.; Hernández-García, C.; Dollar, F.; Mancuso, CA; Peng, P.-C.; Barwick, B.; Gorman, TT; Alonso-Mori, R.; Ališauskas, S.; Andriukaitis, G.; Baltuška, A.; Bostedt, C.; Chen, M.-C.; Dakovski, GL; Durfee, CG; Eckert, S.; Fan, T.-M.; Ferguson, WR; Frischkorn, CG; et al. (2015). «Ультрафиолетовый сюрприз: эффективная генерация мягких рентгеновских лучей высокой гармоники в многократно ионизированной плазме». Science . 350 (6265): 1225–1231. Bibcode : 2015Sci...350.1225P. doi : 10.1126/science.aac9755. hdl : 10366/147088 . PMID  26785483. S2CID  2342988.
24. Попминчев, Т.; Чен, М.-К.; Попминчев Д.; Арпин, П.; Браун, С.; Алисаускас, С.; Андрюкайтис, Г.; Бальчунас, Т.; Мюке, О.Д.; Пагзлис, А.; Балтуска, А.; Шим, Б.; Шраут, SE; Гаэта, А.; Эрнандес-Гарсия, К.; Плайя, Л.; Беккер, А.; Джарон-Беккер, А.; Мурнейн, ММ; и др. (2012). «Яркие когерентные сверхвысокие гармоники в кэВном рентгеновском режиме от фемтосекундных лазеров среднего инфракрасного диапазона». Наука . 336 (6086): 1287–1291. arXiv : 2403.19535 . Bibcode :2012Sci...336.1287P. doi :10.1126/science.1218497. hdl : 10366/147089 . PMID  22679093. S2CID  24628513.
25. Rundquist, A.; Durfee, CG; Chang, Z.; Herne, C.; Backus, S.; Murnane, MM; Kapteyn, HC (1998). "Генерация когерентных мягких рентгеновских лучей с согласованной фазой". Science . 280 (5368): 1412–1415. arXiv : 2403.19636 . Bibcode :1998Sci...280.1412R. doi :10.1126/science.280.5368.1412. PMID  9603725.