Список графиков

Этот частичный список графов содержит определения графов и семейств графов. Для собранных определений терминов теории графов , которые не относятся к отдельным типам графов, таким как вершина и путь , см. Глоссарий теории графов . Для ссылок на существующие статьи о конкретных видах графов см. Категория: Графы . Некоторые из конечных структур, рассматриваемых в теории графов, имеют названия, иногда вдохновленные топологией графа, а иногда в честь их первооткрывателя. Известным примером является граф Петерсена , конкретный граф на 10 вершинах, который появляется как минимальный пример или контрпример во многих различных контекстах.

Индивидуальные графики

Высокосимметричные графы

Сильно регулярные графы

Сильно регулярный граф на v вершинах и ранге k обычно обозначается srg( v,k ,λ,μ).

Симметричные графы

Симметричный граф — это граф, в котором есть симметрия ( автоморфизм графа ), переводящая любую упорядоченную пару смежных вершин в любую другую упорядоченную пару; перепись Фостера перечисляет все малые симметричные 3-регулярные графы. Каждый сильно регулярный граф симметричен, но не наоборот.

Полусимметричные графы

Графические семейства

Полные графики

Полный граф на вершинах часто называют -кликой и обычно обозначают , от немецкого komplett . ^[1] $n$ $n$ $K_{n}$

$К_{1}$
$К_{2}$
$К_{3}$
$К_{4}$
$К_{5}$
$К_{6}$
$K_{7}$
$K_{8}$

Полные двудольные графы

Полный двудольный граф обычно обозначается . Для получения более подробной информации см. раздел о звездных графах. Граф равен 4-циклу (квадрату), представленному ниже. $K_{н,м}$ $n=1$ $К_{2,2}$ $C_{4}$

$К_{2,3}$
$К_{3,3}$ , график полезности
$K_{2,4}$
$K_{3,4}$

Циклы

Граф -цикл на вершинах называется n-циклом и обычно обозначается . Его также называют циклическим графом , многоугольником или n-угольником . Частными случаями являются треугольник , квадрат , а затем несколько с греческими названиями пятиугольник , шестиугольник и т. д. $n$ $C_{n}$ $C_{3}$ $C_{4}$ $C_{5}$ $C_{6}$

$C_{3}$
$C_{4}$
$C_{5}$
$C_{6}$

Графики дружбы

Граф дружбы F _n может быть построен путем соединения n копий графа-цикла C ₃ с общей вершиной. ^[2]

Графы фуллеренов

В теории графов термин фуллерен относится к любому 3- регулярному плоскому графу со всеми гранями размера 5 или 6 (включая внешнюю грань). Из формулы многогранника Эйлера , V – E + F = 2 (где V , E , F обозначают число вершин, ребер и граней), следует, что в фуллерене ровно 12 пятиугольников и h = V /2 – 10 шестиугольников. Следовательно, V = 20 + 2 h ; E = 30 + 3 h . Графы фуллеренов являются представлениями Шлегеля соответствующих соединений фуллеренов.

20-фуллерен ( додекаэдрический граф)
24-фуллерен ( граф гексагонального усеченного трапецоэдра )
26-фуллереновый граф
60-фуллерен ( усеченный икосаэдрический граф)
70-фуллерен

Алгоритм для генерации всех неизоморфных фуллеренов с заданным числом шестиугольных граней был разработан Г. Бринкманном и А. Дрессом. ^[3] Г. Бринкманн также предоставил свободно доступную реализацию, называемую fullgen.

Платоновы тела

Полный граф на четырех вершинах образует скелет тетраэдра , а в более общем случае полные графы образуют скелеты симплексов . Графы гиперкуба также являются скелетами правильных многогранников большей размерности .

Куб ,
$n=8$ $м=12$
Октаэдр ,
$n=6$ $м=12$
Додекаэдр ,
$n=20$ $м=30$
Икосаэдр ,
$n=12$ $м=30$

Усеченные тела

Снаркс

Снарк — это кубический граф без мостов , который требует четырех цветов в любой правильной раскраске ребер . Наименьший снарк — это граф Петерсена , уже перечисленный выше.

Звезда

Звезда S k — это полный двудольный граф K _1,_k . Звезда S ₃ называется графом-клешней _.

Колесные графики

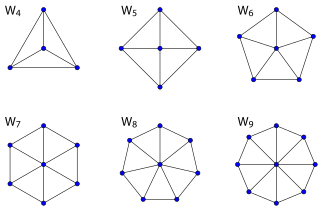
Граф -колесо W _n — это граф на n вершинах, построенный путем соединения одной вершины с каждой вершиной в ( n − 1)-цикле.

Другие графики

Этот частичный список содержит определения графов и семейств графов, которые известны под определенными названиями, но не имеют собственной статьи в Википедии.

Механизм

Шестеренчатый граф , обозначаемый G _n , представляет собой граф, полученный путем вставки дополнительной вершины между каждой парой смежных вершин на периметре колесного графа W _n . Таким образом, G _n имеет 2 n +1 вершин и 3 n ребер. ^[4] Шестеренчатые графы являются примерами квадратных графов и играют ключевую роль в характеристике запрещенных графов квадратных графов. ^[5] Шестеренчатые графы также известны как зубчатые колеса и двудольные колеса .

Шлем

Граф -штурвал , обозначаемый H _n , представляет собой граф, полученный путем присоединения одного ребра и узла к каждому узлу внешнего контура графа -колеса W _n . ^[6]^[7]

Омар

Граф лобстера — это дерево , в котором все вершины находятся в пределах расстояния 2 от центрального пути . ^[8]^[9] Сравните с гусеницей .

Веб

Веб - граф W _{n , r} — это граф, состоящий из r концентрических копий циклического графа C _n , с соответствующими вершинами, соединенными «спицами». Таким образом, W _{n ,1} — это тот же граф, что и C _n , а W _n,2 — это призма .

Веб-граф также определяется как призматический граф Y _{n +1, 3} с удаленными ребрами внешнего цикла. ^[7]^[10]

Ссылки

^ Дэвид Грайс и Фред Б. Шнайдер, Логический подход к дискретной математике , Springer, 1993, стр. 436.
^ Галлиан, JA «Динамический обзор DS6: маркировка графов». Электронный журнал комбинаторики , DS6, 1-58, 3 января 2007 г. [1] Архивировано 31 января 2012 г. на Wayback Machine .
^ Бринкманн, Гуннар; Дресс, Андреас ВМ (1997). «Конструктивное перечисление фуллеренов». Журнал алгоритмов . 23 (2): 345–358. doi :10.1006/jagm.1996.0806. MR 1441972.
^ Вайсштейн, Эрик В. "Граф шестерен". MathWorld .
^ Бандельт, Х.-Дж.; Чепои, В.; Эппштейн, Д. (2010), «Комбинаторика и геометрия конечных и бесконечных квадратных графов», SIAM Journal on Discrete Mathematics , 24 (4): 1399–1440, arXiv : 0905.4537 , doi : 10.1137/090760301, S2CID 10788524
^ Вайсштейн, Эрик В. «Граф Хелма». MathWorld .
^ ab "Архивная копия" (PDF) . Архивировано из оригинала (PDF) 2012-01-31 . Получено 2008-08-16 .{{cite web}}: CS1 maint: архивная копия как заголовок ( ссылка )
^ "Google Дискуссионная группа" . Проверено 5 февраля 2014 г.
^ Вайсштейн, Эрик В. Graph.html "Граф лобстера". MathWorld . {{cite web}}: Проверить |url=значение ( помощь )
^ Вайсштейн, Эрик В. «Веб-график». Математический мир .