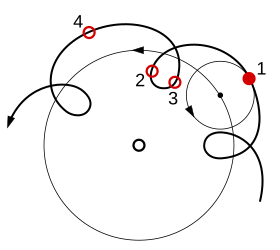
В системах астрономии Гиппарха , Птолемея и Коперника эпицикл (от древнегреческого ἐπίκυκλος ( epíkuklos ) « на круге», что означает «круг, движущийся по другому кругу») [ 1] был геометрической моделью, используемой для объяснения изменений скорости и направления видимого движения Луны , Солнца и планет . В частности, он объяснял видимое ретроградное движение пяти планет, известных в то время. Во-вторых, он также объяснял изменения видимых расстояний планет от Земли.
Впервые предложена Аполлонием Пергским в конце III в. до н. э. Она была развита Аполлонием Пергским и Гиппархом Родосским, которые широко ее использовали во II в. до н. э., затем формализована и широко использовалась Птолемеем в его астрономическом трактате II в. н. э. « Альмагест» .
Эпициклическое движение используется в Антикитерском механизме , [требуется ссылка] древнегреческом астрономическом устройстве, для компенсации эллиптической орбиты Луны, движущейся быстрее в перигее и медленнее в апогее, чем круговые орбиты, с использованием четырех шестерен, две из которых включены эксцентрично, что довольно близко соответствует второму закону Кеплера .
Эпициклы работали очень хорошо и были очень точными, потому что, как позже показал анализ Фурье , любая гладкая кривая может быть аппроксимирована с произвольной точностью с достаточным количеством эпициклов. Однако они вышли из моды с открытием того, что планетарные движения были в значительной степени эллиптическими из гелиоцентрической системы отсчета , что привело к открытию того, что гравитация, подчиняющаяся простому закону обратных квадратов, могла бы лучше объяснить все планетарные движения.
В обеих системах Гиппарха и Птолемея предполагается , что планеты движутся по малой окружности, называемой эпициклом , которая в свою очередь движется по большей окружности, называемой деферентом (сам Птолемей описал эту точку, но не дал ей названия [2] ). Обе окружности вращаются на восток и примерно параллельны плоскости видимой орбиты Солнца в этих системах ( эклиптике ). Несмотря на то, что система считается геоцентрической , ни одна из окружностей не была центрирована на Земле, вместо этого движение каждой планеты было сосредоточено в специфической для планеты точке, немного удаленной от Земли, называемой эксцентриком . Орбиты планет в этой системе похожи на эпитрохоиду , но не являются в точности эпитрохоидами, поскольку угол эпицикла не является линейной функцией угла деферента.
В системе Гиппарха эпицикл вращался и вращался вдоль деферента с равномерным движением. Однако Птолемей обнаружил, что он не может согласовать это с доступными ему данными вавилонских наблюдений; в частности, форма и размер видимых ретроградов отличались. Угловая скорость, с которой двигался эпицикл, не была постоянной, если только он не измерял ее из другой точки, которая теперь называется эквантом ( Птолемей не дал ей названия). Постоянной была угловая скорость, с которой деферент двигался вокруг точки на полпути между эквантом и Землей (эксцентрик); центр эпицикла описывал равные углы за равное время только при наблюдении со стороны экванта. Именно использование эквантов для отделения равномерного движения от центра круговых деферентов отличало систему Птолемея. Для внешних планет угол между центром эпицикла и планетой был таким же, как угол между Землей и Солнцем.
Птолемей не предсказал относительные размеры планетарных деферентов в Альмагесте . Все его вычисления были сделаны относительно нормализованного деферента, рассматривая один случай за раз. Это не значит, что он считал, что все планеты были равноудалены, но у него не было основы для измерения расстояний, за исключением Луны. Он обычно упорядочивал планеты по направлению от Земли на основе их орбитальных периодов. Позже он вычислил их расстояния в Планетарных гипотезах и суммировал их в первом столбце этой таблицы: [3]
Если бы его значения радиусов смещения относительно расстояния Земля-Солнце были более точными, размеры эпициклов все приближались бы к расстоянию Земля-Солнце. Хотя все планеты рассматриваются отдельно, все они связаны одним особым образом: линии, проведенные от тела через эпицентрический центр всех планет, были параллельны, как и линия, проведенная от Солнца к Земле, вдоль которой располагались Меркурий и Венера. Это означает, что все тела вращаются по своим эпициклам в ногу с Солнцем Птолемея (то есть все они имеют период ровно в один год). [ необходима цитата ]
Вавилонские наблюдения показали, что для высших планет планета обычно двигалась по ночному небу медленнее, чем звезды. Каждую ночь планета, казалось, немного отставала от звезд, в том, что называется прямым движением . Вблизи противостояния планета, казалось, меняла направление и двигалась по ночному небу быстрее звезд в течение некоторого времени в ретроградном движении, прежде чем снова повернуть назад и возобновить прямое движение. Эпициклическая теория, в частности, пыталась объяснить это поведение.
Нижние планеты всегда наблюдались вблизи Солнца, появляясь только незадолго до восхода или вскоре после заката. Их видимое ретроградное движение происходит во время перехода от вечерней звезды к утренней звезде, когда они проходят между Землей и Солнцем.
Когда древние астрономы смотрели на небо, они видели Солнце, Луну и звезды, движущиеся над головой в регулярной манере. Вавилоняне проводили небесные наблюдения, в основном за Солнцем и Луной, как средство перекалибровки и сохранения хронометража для религиозных церемоний. [4] Другие ранние цивилизации, такие как греки, имели таких мыслителей, как Фалес Милетский , первый, кто задокументировал и предсказал солнечное затмение (585 г. до н. э.), [5] или Гераклид Понтийский . Они также видели «странников» или «планеты» (наши планеты ). Регулярность в движениях блуждающих тел предполагала, что их положения могли быть предсказуемыми.

Наиболее очевидным подходом к проблеме прогнозирования движений небесных тел было простое нанесение их положений на карту звездного поля, а затем подгонка математических функций под изменяющиеся положения. [6] Введение лучших небесных измерительных приборов, таких как введение гномона Анаксимандром , [7] позволило грекам лучше понять ход времени, например, количество дней в году и продолжительность сезонов, [8] что необходимо для астрономических измерений.
Древние работали с геоцентрической точки зрения по той простой причине, что Земля была там, где они стояли и наблюдали за небом, и именно небо казалось движущимся, в то время как земля под ногами казалась неподвижной и устойчивой. Некоторые греческие астрономы (например, Аристарх Самосский ) предполагали, что планеты (включая Землю) вращаются вокруг Солнца, но оптика (и конкретная математика — например, закон тяготения Исаака Ньютона ) , необходимая для предоставления данных, которые убедительно подтверждали бы гелиоцентрическую модель, не существовали во времена Птолемея и не появятся еще более полутора тысяч лет после его времени. Более того, аристотелевская физика не была разработана с учетом подобных расчетов, а философия Аристотеля относительно небес полностью противоречила концепции гелиоцентризма. Только после того, как Галилео Галилей наблюдал луны Юпитера 7 января 1610 года и фазы Венеры в сентябре 1610 года, гелиоцентрическая модель начала получать широкую поддержку среди астрономов, которые также пришли к принятию идеи о том, что планеты являются отдельными мирами, вращающимися вокруг Солнца (то есть, что Земля также является планетой). Иоганн Кеплер сформулировал свои три закона движения планет , которые описывают орбиты планет в Солнечной системе с замечательной степенью точности, используя систему, которая использует эллиптические, а не круговые орбиты. Три закона Кеплера до сих пор преподаются на университетских курсах физики и астрономии, и формулировка этих законов не изменилась с тех пор, как Кеплер впервые сформулировал их четыреста лет назад.
Видимое движение небесных тел относительно времени имеет циклическую природу. Аполлоний Пергский (III в. до н. э.) понял, что это циклическое изменение можно визуально представить малыми круговыми орбитами, или эпициклами , вращающимися по большим круговым орбитам, или деферентам . Гиппарх (II в. до н. э.) рассчитал требуемые орбиты. Деференты и эпициклы в древних моделях не представляли собой орбиты в современном смысле, а скорее сложный набор круговых путей, центры которых разделены определенным расстоянием, чтобы аппроксимировать наблюдаемое движение небесных тел.
Клавдий Птолемей усовершенствовал концепцию деферента и эпицикла и ввел эквант как механизм, который учитывает изменения скорости в движении планет. Разработанная им эмпирическая методология оказалась необычайно точной для своего времени и все еще использовалась во времена Коперника и Кеплера. Гелиоцентрическая модель не обязательно более точна как система для отслеживания и прогнозирования движений небесных тел, чем геоцентрическая, при рассмотрении строго круговых орбит. Гелиоцентрическая система потребовала бы более сложных систем для компенсации смещения точки отсчета. Только после предложения Кеплера об эллиптических орбитах такая система стала все более точной, чем простая эпициклическая геоцентрическая модель. [9]
Оуэн Джинджерич [10] описывает планетарное соединение, которое произошло в 1504 году и, по-видимому, наблюдалось Коперником. В заметках, приложенных к его копии Альфонсинских таблиц , Коперник прокомментировал, что «Марс превосходит числа более чем на два градуса. Сатурн превосходит числа на полтора градуса». Используя современные компьютерные программы, Джинджерич обнаружил, что во время соединения Сатурн действительно отставал от таблиц на полтора градуса, а Марс опережал предсказания почти на два градуса. Более того, он обнаружил, что предсказания Птолемея для Юпитера в то же время были довольно точными. Таким образом, Коперник и его современники использовали методы Птолемея и считали их заслуживающими доверия более чем через тысячу лет после публикации оригинальной работы Птолемея.
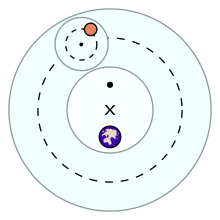
Когда Коперник преобразовал земные наблюдения в гелиоцентрические координаты, [11] он столкнулся с совершенно новой проблемой. Положения, центрированные на Солнце, демонстрировали циклическое движение по отношению ко времени, но без ретроградных петель в случае внешних планет. [ сомнительно – обсудить ] В принципе, гелиоцентрическое движение было проще, но с новыми тонкостями из-за еще не открытой эллиптической формы орбит. Другое осложнение было вызвано проблемой, которую Коперник так и не решил: правильный учет движения Земли в преобразовании координат. [12] : 267 В соответствии с прошлой практикой Коперник использовал модель деферента/эпицикла в своей теории, но его эпициклы были маленькими и назывались «эпициклетами».
В системе Птолемея модели для каждой из планет были разными, и так было с первоначальными моделями Коперника. Однако, работая над математикой, Коперник обнаружил, что его модели можно объединить в единую систему. Более того, если бы они были масштабированы так, чтобы орбита Земли была одинаковой во всех них, порядок планет, который мы распознаем сегодня, легко следовал бы из математики. Меркурий вращался ближе всего к Солнцу, а остальные планеты встали на свои места в порядке, направленном наружу, упорядоченные по их периодам обращения. [12] : 54
Хотя модели Коперника значительно уменьшили величину эпициклов, были ли они проще, чем у Птолемея, спорно. Коперник устранил несколько оклеветанную эквант Птолемея, но ценой дополнительных эпициклов. Различные книги 16-го века, основанные на Птолемее и Копернике, используют примерно равное количество эпициклов. [13] [14] [15] Идея о том, что Коперник использовал только 34 окружности в своей системе, исходит из его собственного заявления в предварительном неопубликованном наброске под названием Commentariolus . К тому времени, как он опубликовал De revolutionibus orbium coelestium , он добавил больше окружностей. Подсчитать общее количество сложно, но, по оценкам, он создал систему столь же сложную, или даже более сложную. [16] Кестлер в своей истории человеческого видения вселенной приравнивает число эпициклов, используемых Коперником, к 48. [17] Популярное общее число около 80 окружностей для системы Птолемея, по-видимому, появилось в 1898 году. Возможно, оно было вдохновлено нептолемеевой системой Джироламо Фракасторо , который использовал либо 77, либо 79 сфер в своей системе, вдохновленной Евдоксом Книдским . [18] Коперник в своих работах преувеличивал число эпициклов, используемых в системе Птолемея; хотя первоначальное количество составляло 80 окружностей, ко времени Коперника система Птолемея была обновлена Пейрбахом до похожего числа 40; таким образом, Коперник фактически заменил проблему ретроградности дополнительными эпициклами. [19]
Теория Коперника была по крайней мере такой же точной, как теория Птолемея, но так и не достигла статуса и признания теории Птолемея. Нужна была теория эллиптической орбиты Кеплера, опубликованная только в 1609 и 1619 годах. Работа Коперника дала объяснения таким явлениям, как ретроградное движение, но на самом деле не доказала, что планеты действительно вращаются вокруг Солнца.

Теории Птолемея и Коперника доказали долговечность и приспособляемость устройства деферента/эпицикла для представления движения планет. Модели деферента/эпицикла работали так хорошо, как они работали, благодаря необычайной орбитальной стабильности Солнечной системы. Любая из этих теорий могла бы использоваться сегодня, если бы Готфрид Вильгельм Лейбниц и Исаак Ньютон не изобрели исчисление . [20]
Согласно Маймониду , в ныне утерянной астрономической системе Ибн Баджи в Андалусской Испании XII века отсутствовали эпициклы. Герсонид из Франции XIV века также исключил эпициклы, утверждая, что они не согласуются с его наблюдениями. [21] Несмотря на эти альтернативные модели, эпициклы не были устранены до XVII века, когда модель эллиптических орбит Иоганна Кеплера постепенно заменила модель Коперника, основанную на идеальных окружностях.
Ньютоновская или классическая механика полностью устранила необходимость в методах деферент/эпицикл и создала более точные теории. Рассматривая Солнце и планеты как точечные массы и используя закон всемирного тяготения Ньютона , были выведены уравнения движения, которые можно было решить различными способами для вычисления прогнозов орбитальных скоростей и положений планет. Если их аппроксимировать как простые задачи двух тел , например, их можно было решить аналитически, в то время как более реалистичная задача n тел требовала численных методов для решения.
Сила ньютоновской механики в решении проблем орбитальной механики проиллюстрирована открытием Нептуна . Анализ наблюдаемых возмущений на орбите Урана дал оценки предполагаемого положения планеты в пределах градуса от того места, где она была обнаружена. Этого нельзя было достичь с помощью методов деферент/эпицикла. Тем не менее, Ньютон в 1702 году опубликовал Теорию движения Луны , которая использовала эпицикл и оставалась в употреблении в Китае до девятнадцатого века. Последующие таблицы, основанные на теории Ньютона, могли приближаться к точности до угловых минут. [22]
Согласно одной из школ мысли в истории астрономии, незначительные несовершенства в исходной системе Птолемея были обнаружены посредством наблюдений, накопленных с течением времени. Ошибочно считалось, что больше уровней эпициклов (кругов внутри кругов) были добавлены к моделям, чтобы точнее соответствовать наблюдаемым движениям планет. Считается, что умножение эпициклов привело к почти неработоспособной системе к XVI веку, и что Коперник создал свою гелиоцентрическую систему , чтобы упростить астрономию Птолемея своего времени, таким образом преуспев в радикальном сокращении числа кругов.
С улучшением наблюдений для представления вновь наблюдаемых явлений стали использоваться дополнительные эпициклы и эксцентрики, пока в позднее Средневековье вселенная не стала «Сферой/С начертанными сверху Центром и Эксцентриком,/Циклом и Эпициклом, Сферой в Сфере».
— Дороти Стимсон , Постепенное принятие теории Коперника о Вселенной , 1917 [23]
В качестве меры сложности число окружностей приводится как 80 для Птолемея, против всего лишь 34 для Коперника. [24] Наибольшее число появилось в Британской энциклопедии по астрономии в 1960-х годах, в обсуждении интереса короля Альфонсо X Кастильского к астрономии в 13 веке. (Альфонсо приписывают заказ на Таблицы Альфонса .)
К этому времени каждая планета была снабжена от 40 до 60 эпициклами, чтобы представить ее сложное движение среди звезд. Пораженный сложностью проекта, Альфонсо приписывают замечание, что если бы он присутствовал при сотворении мира, он мог бы дать превосходный совет.
- Британская энциклопедия , 1968 г. [25]
Как оказалось, главная трудность этой теории эпициклов-на-эпициклах заключается в том, что историки, изучающие книги по астрономии Птолемея из Средних веков и эпохи Возрождения, не нашли абсолютно никаких следов использования нескольких эпициклов для каждой планеты. Например, Альфонсинские таблицы, по-видимому, были рассчитаны с использованием оригинальных, не приукрашенных методов Птолемея. [12] : 57
Другая проблема заключается в том, что сами модели не поощряли никаких доработок. В модели деферент-и-эпицикла части целого взаимосвязаны. Изменение параметра для улучшения соответствия в одном месте нарушит соответствие в другом месте. Модель Птолемея, вероятно, оптимальна в этом отношении. В целом она дала хорошие результаты, но немного упускала кое-где. Опытные астрономы заметили бы эти недостатки и допустили бы их.
По словам историка науки Норвуда Рассела Хэнсона :
Не существует ни одной двусторонне-симметричной или эксцентрично-периодической кривой, используемой в какой-либо области астрофизики или наблюдательной астрономии, которую нельзя было бы гладко изобразить как результирующее движение точки, вращающейся внутри созвездия эпициклов, конечного числа, вращающихся вокруг фиксированного деферента.
— Норвуд Рассел Хэнсон , «Математическая сила эпициклической астрономии», 1960 [26]
Любой путь — периодический или нет, замкнутый или открытый — может быть представлен бесконечным числом эпициклов. Это потому, что эпициклы могут быть представлены в виде комплексного ряда Фурье ; следовательно, при большом числе эпициклов очень сложные пути могут быть представлены в комплексной плоскости . [27]
Пусть комплексное число
где a 0 и k 0 — константы, i = √ −1 — мнимая единица , а t — время, соответствуют дифференту с центром в начале комплексной плоскости и вращающемуся с радиусом a 0 и угловой скоростью
где T — период .
Если z 1 — путь эпицикла, то деферент плюс эпицикл представляется в виде суммы
Это почти периодическая функция , и является периодической функцией только тогда, когда отношение констант k j рационально . Обобщение на N эпициклов дает почти периодическую функцию
который является периодическим только тогда, когда каждая пара k j рационально связана. Нахождение коэффициентов a j для представления зависящего от времени пути в комплексной плоскости , z = f ( t ) , является целью воспроизведения орбиты с деферентами и эпициклами, и это способ « сохранения явлений » (σώζειν τα φαινόμενα). [28]
Эту параллель отметил Джованни Скиапарелли . [29] [30] В контексте дебатов Коперниканской революции о « спасении явлений » вместо предложения объяснений можно понять, почему Фома Аквинский в XIII веке писал:
Разум может быть использован двумя способами для установления точки: во-первых, с целью предоставления достаточного доказательства некоторого принципа [...]. Разум используется другим способом, не для предоставления достаточного доказательства принципа, а для подтверждения уже установленного принципа путем демонстрации соответствия его результатов, как в астрономии теория эксцентриков и эпициклов считается установленной, потому что с ее помощью можно объяснить чувственные проявления небесных движений; однако не так, как если бы это доказательство было достаточным, поскольку какая-то другая теория могла бы их объяснить.
- Фома Аквинский , Summa Theologica [31]
Будучи системой, которая в основном использовалась для обоснования геоцентрической модели, за исключением космоса Коперника, модель деферента и эпицикла была предпочтительнее гелиоцентрических идей, которые предлагали Кеплер и Галилей. Более поздние последователи эпициклической модели, такие как Тихо Браге , который учитывал писания Церкви при создании своей модели, [32] были восприняты еще более благосклонно. Тихоническая модель была гибридной моделью, которая смешивала геоцентрические и гелиоцентрические характеристики, с неподвижной Землей, вокруг которой вращались Солнце и Луна, и планеты, вращающиеся вокруг Солнца. Для Браге идея вращающейся и движущейся Земли была невозможной, и писание всегда должно было быть первостепенным и уважаемым. [33] Когда Галилей попытался оспорить систему Тихо Браге, церковь была недовольна тем, что ее взгляды были оспорены. Публикация Галилея не помогла его делу в суде .
«Добавление эпициклов» стало использоваться как уничижительный комментарий в современных научных дискуссиях. Этот термин может использоваться, например, для описания продолжающихся попыток скорректировать теорию, чтобы ее предсказания соответствовали фактам. Существует общепринятая идея, что дополнительные эпициклы были изобретены для смягчения растущих ошибок, которые система Птолемея отмечала по мере того, как измерения становились более точными, особенно для Марса. Согласно этому представлению, эпициклы рассматриваются некоторыми как парадигматический пример плохой науки. [34]
Коперник добавил дополнительный эпицикл к своим планетам, но это было только в попытке устранить эквант Птолемея, который он считал философским разрывом с совершенством небес Аристотеля. Математически второй эпицикл и эквант дают почти одинаковые результаты, и многие астрономы-коперники до Кеплера продолжали использовать эквант, так как математические вычисления были проще. Эпициклы Коперника также были намного меньше, чем у Птолемея, и были необходимы, потому что планеты в его модели двигались по идеальным окружностям. Иоганн Кеплер позже показал, что планеты движутся по эллипсам, что также устранило необходимость в эпициклах Коперника. [35]