В геометрии звездчатый многогранник — это многогранник , обладающий некоторым повторяющимся свойством невыпуклости, придающим ему визуальное качество звезды.
Существует два основных вида звездчатых многогранников:
Математические исследования звездчатых многогранников обычно касаются правильных , однородных многогранников или двойственных им многогранников. Все эти звезды являются самопересекающимися.
Правильные звездчатые многогранники являются самопересекающимися многогранниками. Они могут иметь либо самопересекающиеся грани , либо самопересекающиеся вершинные фигуры .
Существует четыре правильных звездчатых многогранника , известных как многогранники Кеплера–Пуансо . Символ Шлефли { p , q } подразумевает грани с p сторонами и вершинные фигуры с q сторонами. Два из них имеют пентаграммические {5/2} грани, а два — пентаграммические вершинные фигуры.
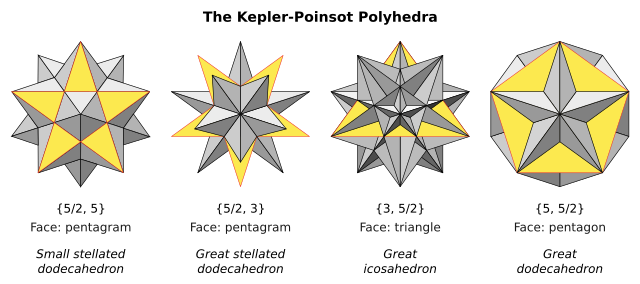
На этих изображениях каждая форма представлена с одним лицом, окрашенным в желтый цвет, чтобы показать видимую часть этого лица.
Существует также бесконечное число правильных звездчатых диэдров и осоэдров {2, p/q } и { p/q ,2} для любого звездчатого многоугольника { p/q }. Будучи вырожденными в евклидовом пространстве, они могут быть реализованы сферически в невырожденной форме.
Существует много однородных звездчатых многогранников , включая две бесконечные серии: призм и антипризм , а также их двойственные .
Однородные и двойственные однородные звездчатые многогранники также являются самопересекающимися многогранниками. Они могут иметь либо самопересекающиеся грани , либо самопересекающиеся вершинные фигуры, либо и то, и другое.
Однородные звездчатые многогранники имеют правильные грани или правильные звездчатые многоугольники . Двойственные однородные звездчатые многогранники имеют правильные грани или правильные звездчатые многоугольники вершинных фигур.
Помимо приведенных выше форм, существует неограниченное количество классов самопересекающихся (звездчатых) многогранников.
Два важных класса — это звёздчатые формы выпуклых многогранников и их двойственные формы, огранки двойственных многогранников.
Например, полная звездчатая форма икосаэдра (на иллюстрации) может быть интерпретирована как самопересекающийся многогранник, состоящий из 20 одинаковых граней, каждая из которых представляет собой (9/4) закрученный многоугольник. Ниже приведена иллюстрация этого многогранника с одной гранью, нарисованной желтым цветом.
Аналогичный самопересекающийся многогранник в любом числе измерений называется звездчатым многогранником .
Правильный многогранник { p , q , r ,..., s , t } является звездчатым многогранником, если либо его грань { p , q ,... s }, либо его вершинная фигура { q , r ,..., s , t } является звездчатым многогранником.
В четырех измерениях 10 правильных звездчатых многогранников называются полихорами Шлефли–Гесса . Аналогично правильным звездчатым многогранникам, все эти 10 состоят из граней, которые являются либо одним из пяти правильных Платоновых тел , либо одним из четырех правильных звездчатых многогранников Кеплера–Пуансо .
Например, большое звездчатое 120-ячейниковое многообразие , спроецированное ортогонально в трехмерное пространство, выглядит следующим образом:
Правильных звездчатых многогранников размерности выше 4 не существует [ необходима ссылка ] .

Многогранник, который не пересекает сам себя, так что вся внутренняя часть может быть видна из одной внутренней точки, является примером звездного домена . Видимые внешние части многих самопересекающихся звездных многогранников образуют границы звездных доменов, но, несмотря на их схожий внешний вид, как абстрактные многогранники это разные структуры. Например, малый звездчатый додекаэдр имеет 12 граней пентаграммы, но соответствующая звездная область имеет 60 равнобедренных треугольных граней и соответственно разное количество вершин и ребер.
Многогранные звездные домены появляются в различных типах архитектуры, обычно религиозной по своей природе. Например, они видны на многих барочных церквях как символы Папы, который построил церковь, на венгерских церквях и на других религиозных зданиях. Эти звезды также могут использоваться в качестве украшений. Моравские звезды используются для обеих целей и могут быть построены в различных формах.