Магнитохимия

Изучение магнитных свойств химических соединений

Магнетохимия занимается магнитными свойствами химических соединений . Магнитные свойства возникают из спина и орбитального углового момента электронов, содержащихся в соединении. Соединения являются диамагнитными, когда они не содержат неспаренных электронов . Молекулярные соединения, которые содержат один или несколько неспаренных электронов, являются парамагнитными . Величина парамагнетизма выражается как эффективный магнитный момент, μ _{eff . Для} переходных металлов первого ряда величина μ _eff является, в первом приближении, простой функцией числа неспаренных электронов, формулой только для спина. В общем случае спин-орбитальная связь заставляет μ _eff отклоняться от формулы только для спина. Для более тяжелых переходных металлов, лантаноидов и актинидов , спин-орбитальную связь нельзя игнорировать. Обменное взаимодействие может происходить в кластерах и бесконечных решетках, что приводит к ферромагнетизму , антиферромагнетизму или ферримагнетизму в зависимости от относительной ориентации отдельных спинов.

Магнитная восприимчивость

Основным измерением в магнетохимии является магнитная восприимчивость. Она измеряет силу взаимодействия при помещении вещества в магнитное поле. Объемная магнитная восприимчивость , представленная символом, определяется соотношением ${\displaystyle \chi _{v}}$

${\displaystyle {\vec {M}}=\chi _{v}{\vec {H}}}$

где, — намагниченность материала ( магнитный дипольный момент на единицу объема), измеряемая в амперах на метр ( единицы СИ ), а — напряженность магнитного поля , также измеряемая в амперах на метр. Восприимчивость — безразмерная величина . Для химических применений предпочтительной величиной является молярная магнитная восприимчивость (χ _моль ). Она измеряется в м ³ ·моль ⁻¹ (СИ) или см ³ ·моль ⁻¹ (СГС) и определяется как ${\displaystyle {\vec {M}}}$ ${\displaystyle {\vec {H}}}$

${\displaystyle \chi _{\text{mol}}=M\chi _{v}/\rho }$

где ρ — плотность в кг·м ⁻³ (СИ) или г·см ⁻³ (СГС), а M — молярная масса в кг·моль ⁻¹ (СИ) или г·моль ⁻¹ (СГС).

Схематическая диаграмма равновесия Гуи

Для измерения магнитной восприимчивости существует множество методов.

• С весами Гуи изменение веса образца измеряется аналитическими весами , когда образец помещается в однородное магнитное поле. Измерения калибруются по известному стандарту, такому как тиоцианат ртути-кобальта, HgCo(NCS) ₄ . Калибровка устраняет необходимость знать плотность образца. Измерения переменной температуры можно проводить, помещая образец в криостат между полюсными наконечниками магнита. ^[1]
• Весы Эванса . ^[2] - это крутильные весы , которые используют образец в фиксированном положении и переменный вторичный магнит для возврата магнитов в исходное положение. Они также калибруются по HgCo(NCS) ₄ .
• С помощью весов Фарадея образец помещается в магнитное поле постоянного градиента и взвешивается на крутильных весах. Этот метод может дать информацию о магнитной анизотропии . ^[3]
• СКВИД — очень чувствительный магнитометр.
• Для веществ в растворе ЯМР может быть использован для измерения восприимчивости. ^{[4] [5]}

Типы магнитного поведения

Когда изолированный атом помещается в магнитное поле, возникает взаимодействие, поскольку каждый электрон в атоме ведет себя как магнит, то есть электрон имеет магнитный момент . Существует два типа взаимодействия.

1. Диамагнетизм. При помещении в магнитное поле атом становится магнитно поляризованным, то есть у него появляется индуцированный магнитный момент. Сила взаимодействия стремится вытолкнуть атом из магнитного поля. По соглашению диамагнитной восприимчивости придается отрицательный знак. Очень часто диамагнитные атомы не имеют неспаренных электронов, то есть каждый электрон спарен с другим электроном на той же атомной орбитали . Моменты двух электронов компенсируют друг друга, поэтому у атома нет чистого магнитного момента. Однако для иона Eu3 ⁺ , имеющего шесть неспаренных электронов, орбитальный угловой момент компенсирует угловой момент электрона, и этот ион диамагнитен при нулевом Кельвине.
2. Парамагнетизм. По крайней мере один электрон не связан с другим. Атом имеет постоянный магнитный момент. При помещении в магнитное поле атом втягивается в это поле. По соглашению парамагнитная восприимчивость имеет положительный знак.

Когда атом присутствует в химическом соединении, его магнитное поведение изменяется под воздействием его химического окружения. Измерение магнитного момента может дать полезную химическую информацию.

В некоторых кристаллических материалах отдельные магнитные моменты могут быть выровнены друг с другом (магнитный момент имеет как величину, так и направление). Это приводит к ферромагнетизму , антиферромагнетизму или ферримагнетизму . Это свойства кристалла в целом, мало влияющие на химические свойства.

Диамагнетизм

Диамагнетизм является универсальным свойством химических соединений, поскольку все химические соединения содержат электронные пары. Соединение, в котором нет неспаренных электронов, называется диамагнитным. Эффект слабый, поскольку он зависит от величины индуцированного магнитного момента. Он зависит от числа электронных пар и химической природы атомов, к которым они принадлежат. Это означает, что эффекты являются аддитивными, и можно составить таблицу «диамагнитных вкладов», или констант Паскаля . ^{[6] [7] [8]} В случае парамагнитных соединений наблюдаемую восприимчивость можно скорректировать, добавив к ней так называемую диамагнитную поправку, которая представляет собой диамагнитную восприимчивость, рассчитанную с использованием значений из таблицы. ^[9]

Парамагнетизм

Механизм и температурная зависимость

Изменение магнитной восприимчивости в зависимости от температуры

Ион металла с одним неспаренным электроном, такой как Cu2 ⁺ , в координационном комплексе представляет собой простейшую иллюстрацию механизма парамагнетизма. Отдельные ионы металла удерживаются лигандами далеко друг от друга, так что между ними нет магнитного взаимодействия. Говорят, что система магнитно разбавлена. Магнитные диполи атомов направлены в случайных направлениях. При приложении магнитного поля происходит расщепление Зеемана первого порядка . Атомы со спинами, выровненными по полю, немного превосходят по численности атомы с невыровненными спинами. В эффекте Зеемана первого порядка разность энергий между двумя состояниями пропорциональна напряженности приложенного поля. Обозначая разность энергий как Δ E , распределение Больцмана дает отношение двух популяций как , где k — постоянная Больцмана , а T — температура в градусах Кельвина . В большинстве случаев Δ E намного меньше kT , и экспоненту можно разложить как 1 – Δ E/kT . Из наличия 1/ T в этом выражении следует, что восприимчивость обратно пропорциональна температуре. ^[10] ${\displaystyle e^{-\Delta E/kT}}$

${\displaystyle \chi ={C \over T}}$

Это известно как закон Кюри , а константа пропорциональности C известна как константа Кюри , значение которой для молярной восприимчивости рассчитывается как ^[11]

${\displaystyle C={\frac {Ng^{2}S(S+1)\mu _{B}^{2}}{3k}}}$

где N — постоянная Авогадро , g — g-фактор Ланде , а μ _B — магнетон Бора . В этой трактовке предполагалось, что основное электронное состояние не вырождено, что магнитная восприимчивость обусловлена ​​только спином электрона и что только основное состояние термически заселено.

В то время как некоторые вещества подчиняются закону Кюри, другие подчиняются закону Кюри-Вейсса .

${\displaystyle \chi ={\frac {C}{T-T_{c}}}}$

T _c — температура Кюри . Закон Кюри-Вейсса будет применяться только при температуре, значительно превышающей температуру Кюри. При температурах ниже температуры Кюри вещество может стать ферромагнитным . Более сложное поведение наблюдается с более тяжелыми переходными элементами.

Эффективный магнитный момент

При соблюдении закона Кюри произведение молярной восприимчивости и температуры является константой. Эффективный магнитный момент μ _eff тогда определяется ^[12] как

${\displaystyle \mu _{\text{eff}}=\mathrm {constant} {\sqrt {T\chi }}}$

Где C имеет единицы СГС см ³ моль ⁻¹ К, μ _эфф равен

${\displaystyle \mu _{\text{eff}}={\sqrt {3k \over N\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 2.82787{\sqrt {T\chi }}}$

Где C имеет единицы СИ м ³ моль ⁻¹ К, μ _эфф равен

${\displaystyle \mu _{\text{eff}}={\sqrt {3k \over N\mu _{0}\mu _{B}^{2}}}{\sqrt {T\chi }}\approx 797.727{\sqrt {T\chi }}}$

Величина μ _eff фактически безразмерна, но часто указывается в единицах магнетон Бора (μ _B ). ^[12]

Для веществ, подчиняющихся закону Кюри, эффективный магнитный момент не зависит от температуры. Для других веществ μ _eff зависит от температуры, но эта зависимость мала, если выполняется закон Кюри-Вейсса и температура Кюри низкая.

Парамагнетизм, не зависящий от температуры

Соединения, которые, как ожидается, будут диамагнитными, могут проявлять этот тип слабого парамагнетизма. Он возникает из-за эффекта Зеемана второго порядка, в котором происходит дополнительное расщепление, пропорциональное квадрату напряженности поля. Его трудно наблюдать, поскольку соединение неизбежно также взаимодействует с магнитным полем в диамагнитном смысле. Тем не менее, имеются данные для перманганат- иона. ^[13] Его легче наблюдать в соединениях более тяжелых элементов, таких как соединения уранила .

Обмен взаимодействиями

Дигидрат ацетата меди(II) ^[14]

Ферримагнитное упорядочение в 2 измерениях

Антиферромагнитное упорядочение в 2 измерениях

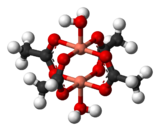
Обменные взаимодействия происходят, когда вещество не является магнитно-разбавленным и существуют взаимодействия между отдельными магнитными центрами. Одной из простейших систем, демонстрирующих результат обменных взаимодействий, является кристаллический ацетат меди(II) , Cu2 ₍ OAc) ₄ (H2O ₎ 2 _. Как следует из формулы, он содержит два иона меди(II). Ионы Cu2 ⁺ удерживаются вместе четырьмя ацетатными лигандами, каждый из которых связывается с обоими ионами меди. Каждый ион Cu2 ^{+ имеет электронную конфигурацию ad9} , и поэтому должен иметь один неспаренный электрон. Если бы между ионами меди была ковалентная связь, электроны бы объединялись в пары, и соединение было бы диамагнитным. Вместо этого существует обменное взаимодействие, при котором спины неспаренных электронов частично выстраиваются друг относительно друга. Фактически создаются два состояния, одно с параллельными спинами, а другое с противоположными спинами. Разница в энергии между двумя состояниями настолько мала, что их заселенности значительно меняются с температурой. В результате магнитный момент изменяется с температурой по сигмоидальной схеме. Состояние с противоположными спинами имеет более низкую энергию, поэтому взаимодействие в этом случае можно классифицировать как антиферромагнитное. ^[14] Считается, что это пример сверхобмена , опосредованного атомами кислорода и углерода ацетатных лигандов. ^[15] Другие димеры и кластеры демонстрируют обменное поведение. ^[16]

Обменные взаимодействия могут действовать на бесконечных цепях в одном измерении, плоскостях в двух измерениях или на всем кристалле в трех измерениях. Это примеры дальнего магнитного упорядочения. Они приводят к ферромагнетизму , антиферромагнетизму или ферримагнетизму в зависимости от природы и относительной ориентации отдельных спинов. ^[17]

Соединения при температурах ниже температуры Кюри проявляют дальний магнитный порядок в форме ферромагнетизма. Другая критическая температура — температура Нееля , ниже которой возникает антиферромагнетизм. Гексагидрат хлорида никеля, NiCl2 _· 6H2O _, имеет температуру Нееля 8,3 К. Восприимчивость максимальна при этой температуре. Ниже температуры Нееля восприимчивость уменьшается, и вещество становится антиферромагнитным. ^[18]

Комплексы ионов переходных металлов

Эффективный магнитный момент для соединения, содержащего ион переходного металла с одним или несколькими неспаренными электронами, зависит от полного орбитального и спинового углового момента неспаренных электронов, и , соответственно. «Полный» в данном контексте означает « векторную сумму ». В приближении, что электронные состояния ионов металла определяются связью Рассела-Саундерса и что спин-орбитальная связь пренебрежимо мала, магнитный момент определяется выражением ^[19] ${\displaystyle {\vec {L}}}$ ${\displaystyle {\vec {S}}}$

${\displaystyle \mu _{\text{eff}}={\sqrt {{\vec {L}}({\vec {L}}+1)+4{\vec {S}}({\vec {S}}+1)}}\mu _{B}}$

Формула только спина

Орбитальный угловой момент генерируется, когда электрон на орбитали вырожденного набора орбиталей перемещается на другую орбиталь в наборе путем вращения. В комплексах с низкой симметрией определенные вращения невозможны. В этом случае орбитальный угловой момент называется «погашенным» и меньше, чем можно было бы ожидать (частичное гашение), или равен нулю (полное гашение). Полное гашение происходит в следующих случаях. Обратите внимание, что электрон в вырожденной паре орбиталей d _{x ² –y ²} или d _{z ²} не может вращаться на другую орбиталь из-за симметрии. ^[20] ${\displaystyle {\vec {L}}}$

легенда: t2g _, t2 ₌ (dxy _{^, dxz} , _dyz ) _. например _, e = ( _{^dx2 – y2 ,} dz2 ^₎ .

Когда орбитальный угловой момент полностью погашен, и парамагнетизм можно отнести только к электронному спину. Полный спиновый угловой момент просто равен половине числа неспаренных электронов, и получается формула только для спина. ${\displaystyle {\vec {L}}=0}$

${\displaystyle \mu _{\text{eff}}={\sqrt {n(n+2)}}\mu _{B}}$

где n — число неспаренных электронов. Формула только спина является хорошим первым приближением для высокоспиновых комплексов переходных металлов первого ряда . ^[21]

Небольшие отклонения от формулы только для спина могут быть результатом пренебрежения орбитальным угловым моментом или спин-орбитальной связью. Например, тетраэдрические комплексы d ³ , d ⁴ , d ⁸ и d ⁹ имеют тенденцию показывать большие отклонения от формулы только для спина, чем октаэдрические комплексы того же иона, поскольку «гашение» орбитального вклада менее эффективно в тетраэдрическом случае. ^[22]

Низкоспиновые комплексы

Диаграмма кристаллического поля для октаэдрического низкоспинового d ⁵

Диаграмма кристаллического поля для октаэдрического высокоспинового d ⁵

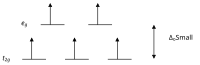
Согласно теории кристаллического поля, d- орбитали иона переходного металла в октаэдрическом комплексе расщепляются на две группы в кристаллическом поле. Если расщепление достаточно велико, чтобы преодолеть энергию, необходимую для размещения электронов на той же орбитали с противоположным спином, получится низкоспиновый комплекс.

При одном неспаренном электроне значения μ _eff находятся в диапазоне от 1,8 до 2,5 μ _B , а при двух неспаренных электронах — в диапазоне от 3,18 до 3,3 μ _B. Обратите внимание, что низкоспиновые комплексы Fe ²⁺ и Co ³⁺ являются диамагнитными. Другая группа комплексов, которые являются диамагнитными, — это квадратно-плоские комплексы ионов d ^{8 ,} таких как Ni ²⁺ и Rh ⁺ и Au ³⁺ .

Спин-кроссовер

Когда разница энергий между высокоспиновыми и низкоспиновыми состояниями сравнима с kT ( k — постоянная Больцмана , а T — температура), между спиновыми состояниями устанавливается равновесие, включающее то, что было названо «электронными изомерами». Трис- дитиокарбамо железа(III), Fe(S2CNR2 ₎ 3 _, является хорошо документированным примером. Эффективный момент варьируется от типичного значения d5 _для ^{низкоспинового} состояния 2,25 _μB при 80 K до более чем 4 _μB выше 300 K. ^[23]

Переходные металлы 2-го и 3-го ряда

Расщепление кристаллического поля больше для комплексов более тяжелых переходных металлов, чем для переходных металлов, обсуждавшихся выше. Следствием этого является то, что низкоспиновые комплексы встречаются гораздо чаще. Константы спин-орбитальной связи, ζ, также больше и не могут игнорироваться даже при элементарных обработках. Магнитное поведение было обобщено, как показано ниже, вместе с обширной таблицей данных. ^[24]

Лантаноиды и актиноиды

Связь Рассела-Саундерса , связь LS, применяется к ионам лантаноидов, эффекты кристаллического поля можно игнорировать, но спин-орбитальная связь не является пренебрежимо малой. Следовательно, спин и орбитальный угловой момент должны быть объединены

${\displaystyle {\vec {L}}=\sum _{i}{\vec {l}}_{i}}$

${\displaystyle {\vec {S}}=\sum _{i}{\vec {s}}_{i}}$

${\displaystyle {\vec {J}}={\vec {L}}+{\vec {S}}}$

и рассчитанный магнитный момент определяется как

${\displaystyle \mu _{\text{eff}}=g{\sqrt {{\vec {J}}({\vec {J}}+1)}};g={3 \over 2}+{\frac {{\vec {S}}({\vec {S}}+1)-{\vec {L}}({\vec {L}}+1)}{2{\vec {J}}({\vec {J}}+1)}}}$

В актинидах спин-орбитальная связь сильна и приближается к связи j j .

${\displaystyle {\vec {J}}=\sum _{i}{\vec {j}}_{i}=\sum _{i}({\vec {l}}_{i}+{\vec {s}}_{i})}$

Это означает, что трудно рассчитать эффективный момент. Например, уран(IV), f ² , в комплексе [UCl ₆ ] ²⁻ имеет измеренный эффективный момент 2,2 μ _B , который включает вклад от температурно-независимого парамагнетизма. ^[26]

Элементы основных групп и органические соединения

Смоделированный спектр ЭПР радикала CH ₃ •

Спин-метка MSTL

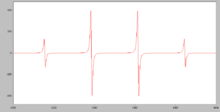
Очень немногие соединения основных групп элементов являются парамагнитными. Известные примеры включают: кислород , O ₂ ; оксид азота , NO; диоксид азота , NO ₂ и диоксид хлора , ClO ₂ . В органической химии соединения с неспаренным электроном называются свободными радикалами . Свободные радикалы, за некоторыми исключениями, являются короткоживущими, потому что один свободный радикал будет быстро реагировать с другим, поэтому их магнитные свойства трудно изучать. Однако, если радикалы хорошо отделены друг от друга в разбавленном растворе в твердой матрице при низкой температуре, их можно изучать с помощью электронного парамагнитного резонанса (ЭПР). Такие радикалы генерируются при облучении. Обширные исследования ЭПР выявили много информации о делокализации электронов в свободных радикалах. Смоделированный спектр радикала CH ₃ • показывает сверхтонкое расщепление из-за взаимодействия электрона с 3 эквивалентными ядрами водорода, каждое из которых имеет спин 1/2. ^{[27] [28]}

Спиновые метки представляют собой долгоживущие свободные радикалы, которые можно вставлять в органические молекулы, чтобы их можно было изучать с помощью ЭПР. ^[29] Например, нитроксид MTSL , функционализированное производное оксида тетраметилпиперидина, TEMPO , используется в направленной спиновой маркировке .

Приложения

Ион гадолиния , Gd3 ⁺ , имеет электронную конфигурацию f7 ^, со всеми параллельными спинами. Соединения иона Gd3 ⁺ являются наиболее подходящими для использования в качестве контрастного вещества для МРТ-сканирования . ^[30] Магнитные моменты соединений гадолиния больше, чем у любого иона переходного металла. Гадолиний предпочтительнее других ионов лантаноидов, некоторые из которых имеют большие эффективные моменты, из-за того, что он имеет невырожденное электронное основное состояние . ^[31]

В течение многих лет природа оксигемоглобина , Hb-O ₂ , была весьма спорной. Экспериментально было обнаружено, что он диамагнитен. Дезоксигемоглобин, как правило, считается комплексом железа в степени окисления +2 , то есть системой ad ⁶ с высокоспиновым магнитным моментом, близким к значению только спина 4,9 μ _B . Было высказано предположение, что железо окисляется, а кислород восстанавливается до супероксида.

Fe(II)Hb (высокоспиновый) + O ₂ ⇌ [Fe(III)Hb]O ₂ ⁻

Затем было предложено, что спаривание электронов от Fe ³⁺ и O ₂ ⁻ происходит посредством обменного механизма. Теперь было показано, что на самом деле железо(II) меняется с высокоспинового на низкоспиновое, когда молекула кислорода отдает пару электронов железу. В то время как в дезоксигемоглобине атом железа лежит над плоскостью гема, в низкоспиновом комплексе эффективный ионный радиус уменьшается, и атом железа лежит в плоскости гема. ^[32]

Fe(II)Hb + O ₂ ⇌ [Fe(II)Hb]O ₂ (низкоспиновый)

Эта информация имеет важное значение для исследований по поиску искусственных переносчиков кислорода .

Соединения галлия(II) были неизвестны до недавнего времени. Поскольку атомный номер галлия — нечетное число (31), Ga2 ⁺ должен иметь неспаренный электрон. Предполагалось, что он будет действовать как свободный радикал и иметь очень короткое время жизни. Отсутствие соединений Ga(II) было частью так называемого эффекта инертной пары . Когда были синтезированы соли аниона с эмпирической формулой, такой как [GaCl3 _] − ^, было обнаружено, что они являются диамагнитными _. Это подразумевало образование связи Ga-Ga и димерной формулы, [Ga2Cl6 _] 2− ^. [ ^33]

Смотрите также

• Магнитная минералогия
• Магнитоэлектрохимия
• Магнитно-ионная жидкость
• Спин-лёд
• Спиновое стекло
• Супердиамагнетизм , Суперпарамагнетизм , Суперферромагнетизм
• Магнетизм одиночной молекулы

Ссылки

1. Эрншоу, стр. 89
2. Весы для измерения магнитной восприимчивости
3. O'Connor, CJ (1982). Lippard, SJ (ред.). Измерения магнитной восприимчивости . Progress in Inorganic Chemistry. Vol. 29. Wiley. p. 203. ISBN 978-0-470-16680-2.
4. Эванс, ДФ (1959). «Определение парамагнитной восприимчивости веществ в растворе методом ядерного магнитного резонанса». J. Chem. Soc. : 2003–2005. doi :10.1039/JR9590002003.
5. Orchard, стр. 15. Earnshshaw, стр. 97.
6. Фиггис и Льюис, стр. 403
7. Карлин, стр. 3
8. Бэйн, Гордон А.; Берри, Джон Ф. (2008). «Диамагнитные поправки и константы Паскаля». J. Chem. Educ . 85 (4): 532. Bibcode : 2008JChEd..85..532B. doi : 10.1021/ed085p532.
9. Фиггис и Льюис, стр. 417
10. Фиггис и Льюис, стр. 419
11. Сад, стр. 48
12. Hoppe, JI (1972). "Эффективный магнитный момент". J. Chem. Educ . 49 (7): 505. Bibcode :1972JChEd..49..505H. doi :10.1021/ed049p505.
13. Сад, стр. 53
14. Lawrence Que (март 2000). Физические методы в бионеорганической химии: спектроскопия и магнетизм. University Science Books. стр. 345–348. ISBN 978-1-891389-02-3. Получено 22 февраля 2011 г.
15. Фиггис и Льюис, с. 435. Фруктовый сад, с. 67
16. Карлин, разделы 5.5–5.7
17. Карлин, главы 6 и 7, стр. 112–225.
18. Карин, стр. 264
19. Фиггис и Льюис, стр. 420
20. Фиггис и Льюис, стр. 424, 432
21. Фиггис и Льюис, стр. 406
22. Фиггис и Льюис, Раздел 3, «Орбитальный вклад»
23. Orchard, стр. 125. Carlin, стр. 270.
24. Фиггис и Льюис, стр. 443–451.
25. Гринвуд и Эрншоу, стр. 1243
26. Сад, стр. 106
27. Weil, John A.; Bolton, James R.; Wertz, John E. (1994). Электронный парамагнитный резонанс: элементарная теория и практические приложения . Wiley. ISBN 0-471-57234-9.
28. Аткинс, П. У.; Саймонс, М. К. Р. (1967). Структура неорганических радикалов; применение электронного спинового резонанса к изучению молекулярной структуры . Elsevier.
29. Берлинер, Л. Дж. (1976). Спиновая маркировка: теория и приложения I. Academic Press. ISBN 0-12-092350-5.Берлинер, Л. Дж. (1979). Спиновая маркировка II: теория и приложения . Academic Press. ISBN 0-12-092352-1.
30. Краузе, В. (2002). Контрастные агенты I: Магнитно-резонансная томография: Ч. 1. Springer. ISBN 3540422471.
31. Караван, Питер; Эллисон, Джеффри Дж.; МакМерри, Томас Дж.; Лауффер, Рэндалл Б., Джеффри Дж.; МакМерри, Томас Дж.; Лауффер, Рэндалл Б. (1999). «Хелаты гадолиния(III) как контрастные агенты для МРТ: структура, динамика и применение». Chem . Rev. 99 (9): 2293–2352. doi :10.1021/cr980440x. PMID  11749483.{{cite journal}}: CS1 maint: несколько имен: список авторов ( ссылка )
32. Гринвуд и Эрншоу, стр. 1099–1011.
33. Гринвуд и Эрншоу, стр. 240

Библиография

• Карлин, Р. Л. (1986). Магнетохимия . Springer . ISBN 978-3-540-15816-5.
• Эрншоу, Алан (1968). Введение в магнетохимию . Academic Press .
• Фиггис, Б. Н.; Льюис, Дж. (1960). «Магнетохимия комплексных соединений». В Льюис. Дж. и Уилкинс. РГ (ред.). Современная координационная химия . Нью-Йорк: Wiley .
• Гринвуд, Норман Н.; Эрншоу, Алан (1997). Химия элементов (2-е изд.). Баттерворт-Хайнеманн . ISBN 978-0-08-037941-8.
• Orchard, AF (2003). Магнетохимия . Oxford Chemistry Primers. Oxford University Press . ISBN 0-19-879278-6.
• Selwood, PW (1943). Магнетохимия. Interscience Publishers Inc.
• Вульфсон, Сергей (1998). Молекулярная магнитохимия . Тейлор и Фрэнсис . ISBN 90-5699-535-9.

Внешние ссылки

• Информационные ресурсы по магнетохимии, доступные в Интернете
• Таблицы диамагнитных поправок и констант Паскаля