Когерентность (физика)

Возможность интерференции двух волн

Когерентность выражает возможность интерференции двух волн . Два монохроматических луча из одного источника всегда интерферируют. ^{[1] : 286} Источники волн не являются строго монохроматическими: они могут быть частично когерентными . Лучи из разных источников взаимно некогерентны .

При интерференции две волны складываются, создавая волну большей амплитуды, чем каждая из них (конструктивная интерференция ), или вычитаются друг из друга, создавая волну минимумов, которая может быть равна нулю ^{[1] : 286} (деструктивная интерференция), в зависимости от их относительной фазы . Конструктивная или деструктивная интерференция являются предельными случаями, и две волны всегда интерферируют, даже если результат сложения сложен или не примечателен.

Две волны с постоянной относительной фазой будут когерентными. ^[2] Степень когерентности можно легко измерить с помощью интерференционной видимости , которая рассматривает размер интерференционных полос относительно входных волн (по мере изменения сдвига фазы); точное математическое определение степени когерентности дается с помощью корреляционных функций. В более общем смысле когерентность описывает статистическое подобие поля (электромагнитного поля, квантового волнового пакета и т. д.) в двух точках пространства или времени. ^[3]

Качественная концепция

Две щели, освещенные одним источником, показывают интерференционную картину. Источник находится далеко слева на схеме, за коллиматорами, которые создают параллельный луч. Эта комбинация гарантирует, что волна от источника ударит по обеим щелям в одной и той же части волнового цикла: волна будет иметь когерентность .

Когерентность контролирует видимость или контрастность интерференционных картин. Например, видимость двухщелевой экспериментальной картины требует, чтобы обе щели были освещены когерентной волной, как показано на рисунке. Большие источники без коллимации или источники, которые смешивают много разных частот, будут иметь более низкую видимость. ^{[4] : 264}

Когерентность содержит несколько различных концепций. Пространственная когерентность описывает корреляцию (или предсказуемую связь) между волнами в разных точках пространства, как поперечную, так и продольную. ^[5] Временная когерентность описывает корреляцию между волнами, наблюдаемыми в разные моменты времени. Оба наблюдаются в эксперименте Майкельсона-Морли и интерференционном эксперименте Юнга . Как только полосы получены в интерферометре Майкельсона , когда одно из зеркал постепенно отодвигается от светоделителя, время прохождения луча увеличивается, а полосы становятся тусклыми и, наконец, исчезают, показывая временную когерентность. Аналогично, в двухщелевом эксперименте , если пространство между двумя щелями увеличивается, когерентность постепенно исчезает, и, наконец, полосы исчезают, показывая пространственную когерентность. В обоих случаях амплитуда полос медленно исчезает, поскольку разность хода увеличивается после длины когерентности.

Когерентность изначально была задумана в связи с двухщелевым экспериментом Томаса Юнга в оптике , но теперь используется в любой области, где используются волны, например, в акустике , электротехнике , нейронауке и квантовой механике . Свойство когерентности является основой для коммерческих приложений, таких как голография , гироскоп Саньяка , радиоантенные решетки , оптическая когерентная томография и телескопические интерферометры ( астрономические оптические интерферометры и радиотелескопы ).

Математическое определение

Функция когерентности между двумя сигналами определяется как ^[6] ${\displaystyle x(t)}$ ${\displaystyle y(t)}$

${\displaystyle \gamma _{xy}^{2}(f)={\frac {|S_{xy}(f)|^{2}}{S_{xx}(f)S_{yy}(f)}}}$

где — кросс-спектральная плотность сигнала, а и — функции спектральной плотности мощности и , соответственно. Кросс-спектральная плотность и спектральная плотность мощности определяются как преобразования Фурье сигналов кросс -корреляции и автокорреляции , соответственно. Например, если сигналы являются функциями времени, кросс-корреляция является мерой сходства двух сигналов как функции временной задержки относительно друг друга, а автокорреляция является мерой сходства каждого сигнала с самим собой в различные моменты времени. В этом случае когерентность является функцией частоты. Аналогично, если и являются функциями пространства, кросс-корреляция измеряет сходство двух сигналов в различных точках пространства, а автокорреляция — сходство сигнала относительно самого себя для определенного расстояния разделения. В этом случае когерентность является функцией волнового числа (пространственной частоты). ${\displaystyle S_{xy}(f)}$ ${\displaystyle S_{xx}(f)}$ ${\displaystyle S_{yy}(f)}$ ${\displaystyle x(t)}$ ${\displaystyle y(t)}$ ${\displaystyle x(t)}$ ${\displaystyle y(t)}$

Когерентность изменяется в интервале . Если это означает, что сигналы идеально коррелированы или линейно связаны, а если они полностью некоррелированы. Если измеряется линейная система, являющаяся входом и выходом, то функция когерентности будет единой по всему спектру. Однако если в системе присутствуют нелинейности, то когерентность будет изменяться в пределе, указанном выше. ${\displaystyle 0\leq \gamma _{xy}^{2}(f)\leq 1}$ ${\displaystyle \gamma _{xy}^{2}(f)=1}$ ${\displaystyle \gamma _{xy}^{2}(f)=0}$ ${\displaystyle x(t)}$ ${\displaystyle y(t)}$

Согласованность и корреляция

Когерентность двух волн выражает, насколько хорошо коррелированы волны, что количественно определяется функцией взаимной корреляции . ^{[7] [1] [8] [9] [10]} Взаимная корреляция количественно определяет способность предсказывать фазу второй волны, зная фазу первой. В качестве примера рассмотрим две волны, идеально коррелированные во все времена (используя монохроматический источник света). В любое время разность фаз между двумя волнами будет постоянной. Если при их объединении они демонстрируют идеальную конструктивную интерференцию, идеальную деструктивную интерференцию или что-то среднее, но с постоянной разностью фаз, то из этого следует, что они идеально когерентны. Как будет обсуждаться ниже, вторая волна не обязательно должна быть отдельной сущностью. Это может быть первая волна в другое время или положение. В этом случае мерой корреляции является функция автокорреляции (иногда называемая самокогерентностью ). Степень корреляции включает в себя корреляционные функции. ^{[11] : 545-550}

Примеры волнообразных состояний

Эти состояния объединяет тот факт, что их поведение описывается волновым уравнением или некоторым его обобщением.

• Волны в канате (вверх и вниз) или пружине (сжатие и расширение)
• Поверхностные волны в жидкости
• Электромагнитные сигналы (поля) в линиях электропередачи
• Звук
• Радиоволны и микроволны
• Световые волны ( оптика )
• Волны материи , связанные, например, с электронами и атомами

В системе с макроскопическими волнами можно измерить волну напрямую. Следовательно, ее корреляцию с другой волной можно просто вычислить. Однако в оптике нельзя измерить электрическое поле напрямую, поскольку оно колеблется намного быстрее, чем временное разрешение любого детектора. ^[12] Вместо этого измеряется интенсивность света. Большинство концепций, связанных с когерентностью, которые будут представлены ниже, были разработаны в области оптики и затем использовались в других областях. Поэтому многие из стандартных измерений когерентности являются косвенными измерениями, даже в областях, где волна может быть измерена напрямую.

Временная когерентность

Рисунок 1: Амплитуда волны одной частоты как функция времени t (красный) и копия той же волны, задержанной на (синий). Время когерентности волны бесконечно, поскольку она идеально коррелирует сама с собой для всех задержек . ^{[13] : 118} ${\displaystyle \tau }$ ${\displaystyle \tau }$

Рисунок 2: Амплитуда волны, фаза которой значительно дрейфует во времени как функция времени t (красный) и копия той же волны, задержанная на (зеленый). ^[14] В любой конкретный момент времени t волна может прекрасно интерферировать со своей задержанной копией. Но, поскольку половину времени красные и зеленые волны находятся в фазе, а половину времени в противофазе, при усреднении по t любая интерференция исчезает при этой задержке. ${\displaystyle \tau _{\mathrm {c} }}$ ${\displaystyle 2\tau }$

Временная когерентность является мерой средней корреляции между значением волны и самой собой, задержанной на , в любую пару времен. Временная когерентность говорит нам, насколько монохроматичным является источник. Другими словами, она характеризует, насколько хорошо волна может интерферировать сама с собой в разное время. Задержка, в течение которой фаза или амплитуда значительно колеблется (и, следовательно, корреляция значительно уменьшается), определяется как время когерентности . При задержке степень когерентности идеальна, тогда как она значительно падает по мере прохождения задержки . Длина когерентности определяется как расстояние, которое волна проходит во времени . ^{[11] : 560, 571–573} ${\displaystyle \tau }$ ${\displaystyle \tau _{\mathrm {c} }}$ ${\displaystyle \tau =0}$ ${\displaystyle \tau =\tau _{\mathrm {c} }}$ ${\displaystyle L_{\mathrm {c} }}$ ${\displaystyle \tau _{\mathrm {c} }}$

Время когерентности не является длительностью сигнала; длина когерентности отличается от области когерентности (см. ниже).

Связь между временем когерентности и полосой пропускания

Чем больше ширина полосы пропускания – диапазон частот Δf, который содержит волна – тем быстрее волна декоррелирует (и, следовательно, тем меньше ): ^{[11] : 358–359, 560} ${\displaystyle \tau _{\mathrm {c} }}$

${\displaystyle \tau _{c}\Delta f\gtrsim 1.}$

Формально это следует из теоремы о свертке в математике, которая связывает преобразование Фурье спектра мощности (интенсивность каждой частоты) с его автокорреляцией. ^{[11] : 572}

Узкополосные лазеры имеют большие длины когерентности (до сотен метров). Например, стабилизированный и мономодовый гелий-неоновый лазер может легко производить свет с длинами когерентности 300 м. ^{[15] Однако не все лазеры обладают высокой монохроматичностью (например, для} лазера на титане-сапфире с синхронизацией мод Δλ ≈ 2 нм – 70 нм).

Светодиоды характеризуются Δλ ≈ 50 нм, а лампы с вольфрамовой нитью накаливания имеют Δλ ≈ 600 нм, поэтому эти источники имеют более короткое время когерентности, чем большинство монохроматических лазеров.

Примеры временной когерентности

Примеры временной согласованности включают в себя:

• Волна, содержащая только одну частоту (монохроматическая), идеально коррелирует сама с собой при всех временных задержках в соответствии с приведенным выше соотношением. (См. рисунок 1)
• Наоборот, волна, фаза которой быстро дрейфует, будет иметь короткое время когерентности. (См. рисунок 2)
• Аналогично, импульсы ( волновые пакеты ) волн, которые по своей природе имеют широкий диапазон частот, также имеют короткое время когерентности, поскольку амплитуда волны быстро меняется. (См. рисунок 3)
• Наконец, белый свет, имеющий очень широкий диапазон частот, представляет собой волну, которая быстро меняется как по амплитуде, так и по фазе. Поскольку он, следовательно, имеет очень короткое время когерентности (всего 10 периодов или около того), его часто называют некогерентным.

Голография требует света с большим временем когерентности. Напротив, оптическая когерентная томография , в своей классической версии, использует свет с коротким временем когерентности.

Измерение временной когерентности

Рисунок 3: Амплитуда волнового пакета, амплитуда которого значительно изменяется во времени (красный), и копия той же волны, задержанная на (зеленый), построенная как функция времени t . В любой конкретный момент времени красная и зеленая волны некоррелированы; одна колеблется, а другая постоянна, поэтому при этой задержке не будет интерференции. Другой способ взглянуть на это — волновые пакеты не перекрываются во времени, поэтому в любой конкретный момент времени есть только одно ненулевое поле, поэтому интерференция не может возникнуть. ${\displaystyle \tau _{\mathrm {c} }}$ ${\displaystyle 2\tau }$

Рисунок 4: Усредненная по времени интенсивность (синий), обнаруженная на выходе интерферометра, отображенная как функция задержки τ для примеров волн на рисунках 2 и 3. При изменении задержки на половину периода интерференция переключается с конструктивной на деструктивную. Черные линии указывают на огибающую интерференции, которая дает степень когерентности . Хотя волны на рисунках 2 и 3 имеют разную временную длительность, они имеют одинаковое время когерентности.

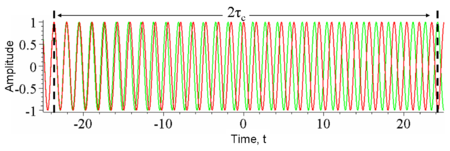
В оптике временная когерентность измеряется в интерферометре, таком как интерферометр Майкельсона или интерферометр Маха-Цендера . В этих устройствах волна объединяется с копией самой себя, которая задерживается на время . Детектор измеряет усредненную по времени интенсивность света, выходящего из интерферометра. Результирующая видимость интерференционной картины (например, см. Рисунок 4) дает временную когерентность при задержке . Поскольку для большинства естественных источников света время когерентности намного короче временного разрешения любого детектора, детектор сам выполняет усреднение по времени. Рассмотрим пример, показанный на рисунке 3. При фиксированной задержке, здесь , бесконечно быстрый детектор будет измерять интенсивность, которая значительно колеблется в течение времени t, равного . В этом случае, чтобы найти временную когерентность при , нужно вручную усреднить интенсивность по времени. ${\displaystyle \tau }$ ${\displaystyle \tau }$ ${\displaystyle 2\tau }$ ${\displaystyle \tau }$ ${\displaystyle 2\tau _{\mathrm {c} }}$

Пространственная когерентность

В некоторых системах, таких как волны на воде или оптика, волноподобные состояния могут распространяться на одно или два измерения. Пространственная когерентность описывает способность двух пространственных точек x ₁ и x ₂ в пределах волны интерферировать при усреднении по времени. Точнее, пространственная когерентность — это взаимная корреляция между двумя точками в волне для всех времен. Если волна имеет только 1 значение амплитуды на бесконечной длине, она идеально пространственно когерентна. Диапазон разделения между двумя точками, на которых наблюдается значительная интерференция, определяет диаметр области когерентности, ^[16] (длина когерентности , часто являющаяся характеристикой источника, обычно является промышленным термином, связанным со временем когерентности источника, а не с областью когерентности в среде). — соответствующий тип когерентности для двухщелевого интерферометра Юнга. Он также используется в оптических системах формирования изображений и, в частности, в различных типах астрономических телескопов. ${\displaystyle A_{\mathrm {c} }}$ ${\displaystyle l_{\mathrm {c} }}$ ${\displaystyle A_{\mathrm {c} }}$

Расстояние от некогерентного источника с площадью поверхности , ${\displaystyle z}$ ${\displaystyle A_{\mathrm {s} }}$ $${\displaystyle A_{\mathrm {c} }={\frac {\lambda ^{2}z^{2}}{A_{\mathrm {s} }}}}$$

Иногда люди также используют термин «пространственная когерентность» для обозначения видимости, когда волнообразное состояние сочетается с пространственно смещенной копией самого себя.

Примеры

• Пространственная когерентность
• 
  Рисунок 5: Плоская волна с бесконечной длиной когерентности .
• 
  Рисунок 6: Волна с переменным профилем (волновым фронтом) и бесконечной длиной когерентности.
• 
  Рисунок 7: Волна с переменным профилем (волновым фронтом) и конечной длиной когерентности.
• 
  Рисунок 8: Волна с конечной площадью когерентности падает на точечное отверстие (малая апертура). Волна будет дифрагировать из точечного отверстия. Вдали от точечного отверстия возникающие сферические волновые фронты приблизительно плоские. Теперь площадь когерентности бесконечна, а длина когерентности неизменна.
• 
  Рисунок 9: Волна с бесконечной областью когерентности объединяется с пространственно смещенной копией самой себя. Некоторые секции волны интерферируют конструктивно, а некоторые будут интерферировать деструктивно. Усредняя по этим секциям, детектор длиной D измерит уменьшенную видимость интерференции . Например, это сделает невыровненный интерферометр Маха-Цендера .

Рассмотрим нить накаливания вольфрамовой лампочки. Различные точки нити накаливания излучают свет независимо и не имеют фиксированного фазового соотношения. Подробно, в любой момент времени профиль излучаемого света будет искажен. Профиль будет изменяться случайным образом в течение времени когерентности . Поскольку для источника белого света, такого как лампочка , он мал, нить накаливания считается пространственно некогерентным источником. Напротив, решетка радиоантенн имеет большую пространственную когерентность, поскольку антенны на противоположных концах решетки излучают с фиксированным фазовым соотношением. Световые волны, создаваемые лазером, часто имеют высокую временную и пространственную когерентность (хотя степень когерентности сильно зависит от точных свойств лазера). Пространственная когерентность лазерных лучей также проявляется в виде спекл-структур и дифракционных полос, видимых на краях тени. ${\displaystyle \tau _{c}}$ ${\displaystyle \tau _{c}}$

Голография требует временно и пространственно когерентного света. Ее изобретатель Деннис Габор создал успешные голограммы более чем за десять лет до изобретения лазеров. Для получения когерентного света он пропустил монохроматический свет из линии излучения ртутной лампы через пространственный фильтр с точечным отверстием.

В феврале 2011 года было сообщено, что атомы гелия , охлажденные до температуры, близкой к абсолютному нулю / состоянию конденсата Бозе-Эйнштейна , могут течь и вести себя как когерентный луч, как это происходит в лазере. ^{[17] [18]} Более того, было обнаружено, что свойства когерентности выходного света из многомодовых нелинейных оптических структур подчиняются оптической термодинамической теории. ^[19]

Спектральная когерентность коротких импульсов

Рисунок 10: Волны разных частот интерферируют, образуя локализованный импульс, если они когерентны.

Рисунок 11: Спектрально некогерентный свет интерферирует, образуя непрерывный свет со случайно изменяющейся фазой и амплитудой.

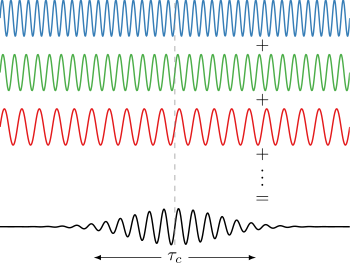
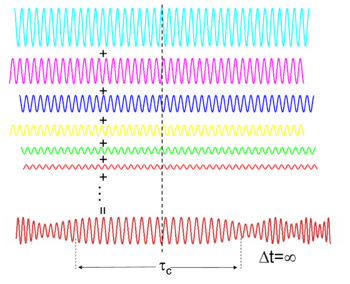
Волны разных частот (в свете это разные цвета) могут интерферировать, образуя импульс, если они имеют фиксированное относительное фазовое соотношение (см. преобразование Фурье ). И наоборот, если волны разных частот не когерентны, то при объединении они создают волну, непрерывную во времени (например, белый свет или белый шум ). Временная длительность импульса ограничена спектральной шириной полосы света в соответствии с: ${\displaystyle \Delta t}$ ${\displaystyle \Delta f}$

${\displaystyle \Delta f\Delta t\geq 1}$,

что следует из свойств преобразования Фурье и приводит к принципу неопределенности Кюпфмюллера (для квантовых частиц это также приводит к принципу неопределенности Гейзенберга ).

Если фаза линейно зависит от частоты (т.е. ), то импульс будет иметь минимальную длительность для своей полосы пропускания ( импульс с ограничением по преобразованию ), в противном случае он будет чирпированным (см. дисперсию ). ${\displaystyle \theta (f)\propto f}$

Измерение спектральной когерентности

Для измерения спектральной когерентности света требуется нелинейный оптический интерферометр, например, оптический коррелятор интенсивности , частотно-разрешенное оптическое стробирование (FROG) или спектральная фазовая интерферометрия для прямой реконструкции электрического поля (SPIDER).

Поляризация и когерентность

Свет также имеет поляризацию , которая является направлением, в котором колеблется электрическое или магнитное поле. Неполяризованный свет состоит из некогерентных световых волн со случайными углами поляризации. Электрическое поле неполяризованного света блуждает во всех направлениях и меняет фазу в течение времени когерентности двух световых волн. Поглощающий поляризатор, повернутый на любой угол, всегда будет пропускать половину падающей интенсивности при усреднении по времени.

Если электрическое поле блуждает на меньшую величину, свет будет частично поляризован, так что под некоторым углом поляризатор будет передавать больше половины интенсивности. Если волна объединяется с ортогонально поляризованной копией самой себя, задержанной на время, меньшее, чем время когерентности, создается частично поляризованный свет.

Поляризация светового луча представлена ​​вектором в сфере Пуанкаре . Для поляризованного света конец вектора лежит на поверхности сферы, тогда как для неполяризованного света вектор имеет нулевую длину. Вектор для частично поляризованного света лежит внутри сферы.

Квантовая когерентность

Характерное свойство квантовых материальных волн , волновая интерференция, основана на когерентности. Хотя изначально она была создана по образцу оптической когерентности, теория и экспериментальное понимание квантовой когерентности значительно расширили эту тему. ^[20]

Когерентность волн материи

Простейшее расширение оптической когерентности применяет оптические концепции к волнам материи . Например, при выполнении эксперимента с двумя щелями с атомами вместо световых волн достаточно коллимированный атомный пучок создает когерентную атомную волновую функцию, освещающую обе щели. ^[21] Каждая щель действует как отдельный, но синфазный пучок, вносящий вклад в картину интенсивности на экране. Эти два вклада приводят к картине интенсивности ярких полос из-за конструктивной интерференции, перемежающейся с темными полосами из-за деструктивной интерференции, на экране ниже по потоку. Было продемонстрировано много вариаций этого эксперимента. ^{[22] : 1057}

Как и в случае со светом, поперечная когерентность (поперек направления распространения) волн материи контролируется коллимацией. Поскольку свет на всех частотах движется с одинаковой скоростью, продольная и временная когерентность связаны; в волнах материи они независимы. В волнах материи выбор скорости (энергии) контролирует продольную когерентность, а пульсация или прерывание контролирует временную когерентность. ^{[21] : 154}

Квантовая оптика

Открытие эффекта Ханбери-Брауна и Твисса – корреляции света при совпадении – побудило Глаубера создать ^[23] уникальный квантовый когерентный анализ. Классическая оптическая когерентность становится классическим пределом для квантовой когерентности первого порядка; более высокая степень когерентности приводит ко многим явлениям в квантовой оптике .

Макроскопическая квантовая когерентность

Макроскопическая масштабная квантовая когерентность приводит к новым явлениям, так называемым макроскопическим квантовым явлениям . Например, лазер , сверхпроводимость и сверхтекучесть являются примерами высококогерентных квантовых систем, эффекты которых очевидны в макроскопическом масштабе. Макроскопическая квантовая когерентность (внедиагональный дальний порядок, ODLRO) ^{[24] [25]} для сверхтекучести и лазерного света связана с когерентностью первого порядка (1-тело)/ODLRO, в то время как сверхпроводимость связана с когерентностью второго порядка/ODLRO. (Для фермионов, таких как электроны, возможны только четные порядки когерентности/ODLRO.) Для бозонов конденсат Бозе–Эйнштейна является примером системы, демонстрирующей макроскопическую квантовую когерентность через множественное занятое одночастичное состояние.

Классическое электромагнитное поле демонстрирует макроскопическую квантовую когерентность. Наиболее очевидным примером является несущий сигнал для радио и телевидения. Они удовлетворяют квантовому описанию когерентности Глаубера .

Квантовая когерентность как ресурс

Недавно MB Plenio и его коллеги построили операциональную формулировку квантовой когерентности как ресурсной теории. Они ввели монотоны когерентности, аналогичные монотонам запутанности. ^[26] Было показано, что квантовая когерентность эквивалентна квантовой запутанности ^[27] в том смысле, что когерентность может быть точно описана как запутанность, и наоборот, что каждая мера запутанности соответствует мере когерентности.

Приложения

Голография

Когерентные суперпозиции оптических волновых полей включают голографию. Голографические фотографии использовались как искусство и как трудно подделываемые защитные этикетки.

Неоптические волновые поля

Дальнейшие приложения касаются когерентной суперпозиции неоптических волновых полей . Например, в квантовой механике рассматривается поле вероятности, которое связано с волновой функцией (интерпретация: плотность амплитуды вероятности). Здесь приложения касаются, среди прочего, будущих технологий квантовых вычислений и уже имеющейся технологии квантовой криптографии . Дополнительно рассматриваются проблемы следующего подраздела. ${\displaystyle \psi (\mathbf {r} )}$

Модальный анализ

Когерентность используется для проверки качества измеряемых передаточных функций (FRF). Низкая когерентность может быть вызвана плохим отношением сигнал/шум и/или недостаточным разрешением по частоте.

Смотрите также

• Атомная когерентность  – тип состояния системы атом-электромагнитное поле
• Длина когерентности  – расстояние, на котором распространяющаяся волна сохраняет определенную степень когерентности.
• Когерентные состояния  – определенное квантовое состояние квантового гармонического осциллятораСтраницы, отображающие краткие описания целей перенаправления
• Ширина линии лазера  – ширина спектральной линии лазерного луча.
• Измерение в квантовой механике  – Взаимодействие квантовой системы с классическим наблюдателем
• Проблема измерения  – Теоретическая проблема квантовой физики
• Монохроматическое излучение  – электромагнитное излучение с одной постоянной частотой.
• Функция взаимной когерентности
• Оптическое гетеродинное обнаружение
• Квантовая биология  – применение квантовой механики и теоретической химии к биологическим объектам и проблемам
• Квантовый эффект Зенона  - явление квантового измерения
• Суперпозиция волн  – фундаментальный физический принцип, утверждающий, что физические решения линейных систем являются линейными.Страницы, отображающие краткие описания целей перенаправления

Ссылки

1. M.Born; E. Wolf (1999). Principles of Optics (7-е изд.). Cambridge University Press . ISBN 978-0-521-64222-4.
2. Рудигер, Пашотта. «Статья о когерентности в энциклопедии RP Photonics». Энциклопедия RP Photonics . Получено 07.06.2023 .
3. Вольф, Эмиль (2007). Введение в теорию когерентности и поляризации света . Кембридж: Cambridge University Press. ISBN 978-0-521-82211-4. OCLC  149011826.
4. Борн, Макс; Вольф, Эмиль (1993). Принципы оптики: электромагнитная теория распространения, интерференции и дифракции света (6-е изд., переиздано (с исправлениями) изд.). Оксфорд: Pergamon Press. ISBN 978-0-08-026481-3.
5. Хехт (1998). Оптика (3-е изд.). Эддисон Уэсли Лонгман. стр. 554–574. ISBN 978-0-201-83887-9.
6. Шин. К., Хаммонд. Дж. Основы обработки сигналов для звуко- и виброинженеров . John Wiley & Sons, 2008.
7. Рольф Г. Винтер; Эфраим М. Стейнберг (2008). «Когерентность». AccessScience . McGraw-Hill . doi :10.1036/1097-8542.146900.
8. Лоудон, Родни (2000). Квантовая теория света . Oxford University Press . ISBN 978-0-19-850177-0.
9. Леонард Мандель; Эмиль Вольф (1995). Оптическая когерентность и квантовая оптика . Cambridge University Press . ISBN 978-0-521-41711-2.
10. Арвинд Маратай (1982). Элементы теории оптической когерентности . John Wiley & Sons . ISBN 978-0-471-56789-9.
11. Хехт, Юджин (2002). Оптика (4-е изд.). Соединенные Штаты Америки: Addison Wesley. ISBN 978-0-8053-8566-3.
12. Пэн, Дж.-Л.; Лю, Т.-А.; Шу, Р.-Х. (2008). «Оптический частотомер на основе двух волоконных лазерных гребенок с синхронизацией мод». Applied Physics B. 92 ( 4): 513. Bibcode : 2008ApPhB..92..513P. doi : 10.1007/s00340-008-3111-6. S2CID  121675431.
13. Кристофер Джерри; Питер Найт (2005). Введение в квантовую оптику . Издательство Кембриджского университета. ISBN 978-0-521-52735-4.
14. Эту фигуру нужно изменить, потому что на ней зеленая волна на самом деле не является копией красной волны; обе являются монохроматическими волнами с немного разными частотами. Правильная фигура была бы комбинацией чирп-волны и ее задержанной копии, чтобы соответствовать фигуре и текущему описанию фигуры.
15. Салех, Тейч. Основы фотоники . Wiley.
16. Гудман (1985). Статистическая оптика (1-е изд.). Wiley-Interscience. стр. 210, 221. ISBN 978-0-471-01502-4.
17. Hodgman, SS; Dall, RG; Manning, AG; Baldwin, KGH; Truscott, AG (2011). «Прямое измерение дальнодействующей когерентности третьего порядка в конденсатах Бозе-Эйнштейна». Science . 331 (6020): 1046–1049. Bibcode :2011Sci...331.1046H. doi :10.1126/science.1198481. PMID  21350171. S2CID  5336898.
18. Pincock, S. (25 февраля 2011 г.). «Холодный лазер заставляет атомы двигаться во времени». ABC Science . ABC News Online . Получено 2011-03-02 .
19. Селим, Махмуд А.; Ву, Фань О.; Пириалакос, Георгиос Г.; Хаджавихан, Мерседех; Христодулидес, Деметриос (2023-03-01). «Свойства когерентности света в многомодовых нелинейных параболических волокнах в условиях оптического равновесия». Optics Letters . 48 (5): 1208–1211. arXiv : 2212.10063 . doi :10.1364/OL.483282. ISSN  1539-4794. PMID  36857250. S2CID  254877557.
20. Стрельцов, Александр; Адессо, Херардо; Пленио, Мартин Б. (2017-10-30). «Коллоквиум: Квантовая когерентность как ресурс». Reviews of Modern Physics . 89 (4): 041003. arXiv : 1609.02439 . doi : 10.1103/RevModPhys.89.041003. ISSN  0034-6861. S2CID  62899253.
21. Адамс, CS; Сигел, M; Млинек, J (май 1994). "Оптика атома". Physics Reports . 240 (3): 143–210. doi : 10.1016/0370-1573(94)90066-3 .
22. Кронин, Александр Д.; Шмидмайер, Йорг; Притчард, Дэвид Э. (28 июля 2009 г.). «Оптика и интерферометрия с атомами и молекулами». Reviews of Modern Physics . 81 (3): 1051–1129. doi :10.1103/RevModPhys.81.1051. hdl : 1721.1/52372 . ISSN  0034-6861. S2CID  28009912.
23. Глаубер, Рой Дж. (1963-06-15). «Квантовая теория оптической когерентности». Physical Review . 130 (6): 2529–2539. doi : 10.1103/PhysRev.130.2529 . ISSN  0031-899X.
24. Пенроуз, О.; Онзагер, Л. (1956). «Бозе-Эйнштейновская конденсация и жидкий гелий». Phys. Rev. 104 ( 3): 576–584. Bibcode :1956PhRv..104..576P. doi :10.1103/physrev.104.576.
25. Yang, CN (1962). «Концепция недиагонального дальнего порядка и квантовые фазы жидкого Не и сверхпроводников». Rev. Mod. Phys . 34 (4): 694–704. Bibcode :1962RvMP...34..694Y. doi :10.1103/revmodphys.34.694.
26. Baumgratz, T.; Cramer, M.; Plenio, MB (2014). "Quantifying Coherence". Phys. Rev. Lett . 113 (14): 140401. arXiv : 1311.0275 . Bibcode : 2014PhRvL.113n0401B. doi : 10.1103/physrevlett.113.140401. PMID  25325620. S2CID  45904642.
27. Tan, KC; Jeong, H. (2018). «Запутанность как симметричная часть коррелированной когерентности». Phys. Rev. Lett . 121 (22): 220401. arXiv : 1805.10750 . Bibcode : 2018PhRvL.121v0401T. doi : 10.1103/PhysRevLett.121.220401. PMID  30547638. S2CID  51690149.

Внешние ссылки

• Доктор СкайСкулл (2008-09-03). "Основы оптики: Когерентность". Черепа в звездах .