stringtranslate.com

Эксперимент с двумя щелями

В современной физике эксперимент с двумя щелями демонстрирует, что свет и материя могут демонстрировать поведение либо классических частиц , либо классических волн . Эта неоднозначность считается доказательством фундаментально вероятностной природы квантовой механики . Этот тип эксперимента был впервые выполнен Томасом Янгом в 1801 году как демонстрация волнового поведения видимого света. [1] В 1927 году Дэвиссон и Джермер и, независимо друг от друга, Джордж Пейджет Томсон и его студент-исследователь Александр Рид [2] продемонстрировали, что электроны демонстрируют такое же поведение, которое позже было распространено на атомы и молекулы. [3] [4] [5] Эксперимент Томаса Юнга со светом был частью классической физики задолго до развития квантовой механики и концепции корпускулярно-волнового дуализма . Он считал, что он продемонстрировал, что волновая теория света Христиана Гюйгенса была правильной, и его эксперимент иногда называют экспериментом Юнга [6] или щелями Юнга. [7]

Эксперимент относится к общему классу экспериментов с «двойным путем», в которых волна разделяется на две отдельные волны (волна обычно состоит из множества фотонов и лучше называть ее волновым фронтом, не путать с волновыми свойствами отдельного фотона), которые затем объединяются в одну волну. Изменения в длине пути обеих волн приводят к сдвигу фаз , создавая интерференционную картину . Другая версия — интерферометр Маха-Цендера , который разделяет луч с помощью светоделителя .

В базовой версии этого эксперимента когерентный источник света , такой как лазерный луч, освещает пластину, пронизанную двумя параллельными щелями, и свет, проходящий через щели, наблюдается на экране за пластиной. [8] [9] Волновая природа света приводит к тому, что световые волны, проходящие через две щели, интерферируют , создавая яркие и темные полосы на экране — результат, который нельзя было бы ожидать, если бы свет состоял из классических частиц. [8] [10] Однако обнаруживается, что свет всегда поглощается на экране в дискретных точках, как отдельные частицы (а не волны); интерференционная картина появляется из-за различной плотности попаданий этих частиц на экран. [11] Кроме того, версии эксперимента, которые включают детекторы на щелях, обнаруживают, что каждый обнаруженный фотон проходит через одну щель (как классическая частица), а не через обе щели (как волна). [12] [13] [14] [15] [16] Однако такие эксперименты показывают, что частицы не формируют интерференционную картину, если определить, через какую щель они проходят. Эти результаты демонстрируют принцип корпускулярно-волнового дуализма . [17] [18]

Обнаружено, что другие объекты атомного масштаба, такие как электроны , демонстрируют такое же поведение при выстреле в двойную щель. [9] Кроме того, обнаружено, что обнаружение отдельных дискретных ударов по своей сути является вероятностным, что необъяснимо с помощью классической механики . [9]

Эксперимент можно провести с сущностями, намного большими, чем электроны и фотоны, хотя это становится сложнее с увеличением размера. Самыми большими сущностями, для которых был проведен эксперимент с двумя щелями, были молекулы , каждая из которых состояла из 2000 атомов (общая масса которых составляла 25 000 атомных единиц массы ). [19]

Эксперимент с двумя щелями (и его вариации) стал классикой благодаря своей ясности в выражении центральных загадок квантовой механики. Ричард Фейнман назвал его «явлением, которое невозможно […] объяснить никаким классическим способом , и которое содержит в себе сердце квантовой механики. В действительности, оно содержит единственную тайну [квантовой механики]». [9]

Обзор

Та же двухщелевая сборка (0,7 мм между щелями); на верхнем изображении одна щель закрыта. На однощелевом изображении дифракционная картина (слабые пятна по обе стороны от основной полосы) формируется из-за ненулевой ширины щели. Эта дифракционная картина также видна на двухщелевом изображении, но со множеством более мелких интерференционных полос.

Если бы свет состоял строго из обычных или классических частиц, и эти частицы выстреливались бы по прямой линии через щель и попадали бы на экран с другой стороны, мы бы ожидали увидеть узор, соответствующий размеру и форме щели. Однако, когда этот «эксперимент с одной щелью» фактически выполняется, узор на экране представляет собой дифракционную картину , в которой свет распространяется. Чем меньше щель, тем больше угол распространения. Верхняя часть изображения показывает центральную часть узора, образованного при освещении щели красным лазером, и, если внимательно присмотреться, две слабые боковые полосы. Больше полос можно увидеть с помощью более совершенного аппарата. Дифракция объясняет узор как результат интерференции световых волн от щели.

Если осветить две параллельные щели, свет от двух щелей снова интерферирует. Здесь интерференция представляет собой более выраженный рисунок с серией чередующихся светлых и темных полос. Ширина полос является свойством частоты освещающего света. [20] (См. нижнюю фотографию справа.)

Рисунок дифракции Юнга

Когда Томас Юнг (1773–1829) впервые продемонстрировал это явление, оно показало, что свет состоит из волн, поскольку распределение яркости можно объяснить попеременной аддитивной и субтрактивной интерференцией волновых фронтов . [9] Эксперимент Юнга, проведенный в начале 1800-х годов, сыграл решающую роль в понимании волновой теории света, одержав победу над корпускулярной теорией света, предложенной Исааком Ньютоном , которая была общепринятой моделью распространения света в 17-м и 18-м веках.

Однако позднее открытие фотоэлектрического эффекта показало, что при различных обстоятельствах свет может вести себя так, как будто он состоит из дискретных частиц. Эти, казалось бы, противоречивые открытия заставили выйти за рамки классической физики и принять во внимание квантовую природу света.

Фейнман любил говорить, что вся квантовая механика может быть почерпнута из тщательного обдумывания последствий этого одного эксперимента. [21] Он также предположил (в качестве мысленного эксперимента), что если бы детекторы были размещены перед каждой щелью, интерференционная картина исчезла бы. [22]

Соотношение дуальности Энглерта –Гринбергера дает подробное описание математики двухщелевой интерференции в контексте квантовой механики.

Двухщелевой эксперимент с низкой интенсивностью света был впервые проведен Г. И. Тейлором в 1909 году [23] путем снижения уровня падающего света до тех пор, пока события испускания/поглощения фотонов не стали в основном неперекрывающимися.Эксперимент по щелевой интерференции не проводился ни с чем, кроме света, до 1961 года, когда Клаус Йонссон из Тюбингенского университета провел его с когерентными электронными пучками и несколькими щелями. [24] [25] В 1974 году итальянские физики Пьер Джорджио Мерли, Джан Франко Миссироли и Джулио Поцци провели связанный эксперимент с использованием отдельных электронов из когерентного источника и бипризменного светоделителя, показав статистическую природу накопления интерференционной картины, как и предсказывала квантовая теория. [26] [27] В 2002 году одноэлектронная версия эксперимента была признана «самым красивым экспериментом» читателями Physics World . [28] С тех пор было опубликовано несколько связанных экспериментов, вызвавших небольшие споры. [29]

В 2012 году Стефано Фраббони и его коллеги отправили отдельные электроны на наноизготовленные щели (шириной около 100 нм) и, обнаружив переданные электроны с помощью одноэлектронного детектора, они смогли показать формирование двухщелевой интерференционной картины. [30] Было проведено много связанных экспериментов с использованием когерентной интерференции; они являются основой современной электронной дифракции, микроскопии и визуализации с высоким разрешением. [31] [32]

В 2018 году в Лаборатории позитронов (L-NESS, Миланский политехнический институт ) Рафаэля Феррагута в Комо ( Италия ) группой под руководством Марко Джаммарки была продемонстрирована интерференция отдельных частиц для антиматерии. [33]

Варианты эксперимента

Интерференция отдельных частиц

Важная версия этого эксперимента включает в себя обнаружение отдельных частиц. Освещение двойной щели с низкой интенсивностью приводит к обнаружению отдельных частиц в виде белых точек на экране. Однако примечательно, что интерференционная картина возникает, когда этим частицам позволяют накапливаться по одной (см. изображение ниже).

Это демонстрирует корпускулярно-волновой дуализм , который гласит, что вся материя проявляет как волновые, так и корпускулярные свойства: частица измеряется как одиночный импульс в одном положении, в то время как квадрат модуля волны описывает вероятность обнаружения частицы в определенном месте на экране, давая статистическую интерференционную картину. [35] Было показано, что это явление происходит с фотонами, [36] электронами, [37] атомами и даже некоторыми молекулами: с бакминстерфуллереном ( C
60) в 2001 году [38] [39] [40] [41] с 2 молекулами из 430 атомов ( C
60(С)
12Ф
25)
10и С
168ЧАС
94Ф
152О
8Н
4С
4) в 2011 году [42] и с молекулами, содержащими до 2000 атомов, в 2019 году [43] . Помимо интерференционных картин, созданных из отдельных частиц, до 4 запутанных фотонов также могут демонстрировать интерференционные картины. [44]

Интерферометр Маха-Цендера

Фотоны в интерферометре Маха-Цендера демонстрируют волнообразную интерференцию и корпускулярное детектирование на детекторах одиночных фотонов .

Интерферометр Маха-Цендера можно рассматривать как упрощенную версию эксперимента с двумя щелями. Вместо того, чтобы распространяться через свободное пространство после двух щелей и попадать в любую точку на расширенном экране, в интерферометре фотоны могут распространяться только по двум путям и попадать в два дискретных фотодетектора. Это позволяет описать его с помощью простой линейной алгебры в размерности 2, а не дифференциальных уравнений.

Фотон, испускаемый лазером, попадает в первый светоделитель и затем находится в суперпозиции между двумя возможными путями. Во втором светоделителе эти пути интерферируют, в результате чего фотон попадает в фотодетектор справа с вероятностью один, а в фотодетектор снизу с вероятностью ноль. Интересно рассмотреть, что бы произошло, если бы фотон определенно находился на одном из путей между светоделителями. Этого можно добиться, заблокировав один из путей или, что эквивалентно, обнаружив наличие там фотона. В обоих случаях больше не будет интерференции между путями, и оба фотодетектора будут поражены с вероятностью 1/2. Из этого мы можем сделать вывод, что фотон не идет по одному или другому пути после первого светоделителя, а находится в настоящей квантовой суперпозиции двух путей. [45]

Эксперименты «в какую сторону» и принцип дополнительности

Известный мысленный эксперимент предсказывает, что если детекторы частиц разместить на щелях, показывая, через какую щель проходит фотон, интерференционная картина исчезнет. [9] Этот эксперимент с выбором пути иллюстрирует принцип дополнительности , согласно которому фотоны могут вести себя либо как частицы, либо как волны, но не могут наблюдаться как оба одновременно. [46] [47] [48] Несмотря на важность этого мысленного эксперимента в истории квантовой механики (например, см. обсуждение версии этого эксперимента Эйнштейна ), технически осуществимые реализации этого эксперимента не предлагались до 1970-х годов. [49] (Наивные реализации мысленного эксперимента из учебника невозможны, поскольку фотоны не могут быть обнаружены без поглощения фотона.) В настоящее время было проведено множество экспериментов, иллюстрирующих различные аспекты дополнительности. [50]

Эксперимент, проведенный в 1987 году [51] [52], дал результаты, которые продемонстрировали, что частичная информация о том, какой путь прошла частица, может быть получена без полного разрушения интерференции. Этот «компромисс волны и частицы» принимает форму неравенства , связывающего видимость интерференционной картины и различимость путей «какого пути». [53]

Отложенный выбор и вариации квантового ластика

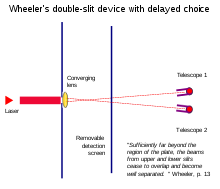
Эксперимент Уиллера с отложенным выбором
Схема эксперимента Уилера с отложенным выбором, показывающая принцип определения пути фотона после его прохождения через щель.

Эксперименты Уилера с отложенным выбором демонстрируют, что извлечение информации о «пути» после того, как частица проходит через щели, может, по-видимому, ретроспективно изменить ее предыдущее поведение в щелях.

Эксперименты с квантовым ластиком демонстрируют, что поведение волны можно восстановить, стерев или иным образом сделав навсегда недоступной информацию о «пути».

Простая иллюстрация явления квантового ластика, которую можно сделать дома, была приведена в статье в Scientific American . [54] Если установить поляризаторы перед каждой щелью с осями, ортогональными друг другу, интерференционная картина будет устранена. Поляризаторы можно рассматривать как вносящие информацию о пути для каждого луча. Введение третьего поляризатора перед детектором с осью 45° относительно других поляризаторов «стирает» эту информацию, позволяя интерференционной картине появиться снова. Это также можно объяснить, рассматривая свет как классическую волну, [54] : 91  , а также при использовании круговых поляризаторов и одиночных фотонов. [55] : 6  Реализации поляризаторов, использующих запутанные пары фотонов, не имеют классического объяснения. [55]

Слабое измерение

В широко разрекламированном эксперименте 2012 года исследователи заявили, что определили путь, по которому прошла каждая частица, без каких-либо неблагоприятных последствий для интерференционной картины, создаваемой частицами. [56] Для этого они использовали установку, при которой частицы, попадающие на экран, были не из точечного источника, а из источника с двумя максимумами интенсивности. Однако комментаторы, такие как Свенссон [57], указали, что на самом деле нет никакого конфликта между слабыми измерениями, выполненными в этом варианте эксперимента с двумя щелями, и принципом неопределенности Гейзенберга . Слабое измерение с последующим пост-отбором не позволяло одновременно измерять положение и импульс для каждой отдельной частицы, но позволяло измерять среднюю траекторию частиц, прибывших в разные положения. Другими словами, экспериментаторы создавали статистическую карту полного ландшафта траектории. [57]

Другие вариации

Лабораторная двухщелевая сборка; расстояние между верхними стойками составляет примерно 2,5 см (один дюйм).
Картины распределения интенсивности в ближнем поле для плазмонных щелей с одинаковой шириной (A) и неравной шириной (B).

В 1967 году Пфлейгор и Мандель продемонстрировали интерференцию двух источников, используя два отдельных лазера в качестве источников света. [58] [59]

В 1972 году было экспериментально показано, что в двухщелевой системе, где в любой момент времени открыта только одна щель, интерференция все равно наблюдается при условии, что разность путей такова, что обнаруженный фотон мог прийти из любой щели. [60] [61] Экспериментальные условия были таковы, что плотность фотонов в системе была намного меньше 1.

В 1991 году Карнал и Млинек провели классический эксперимент Юнга с двумя щелями, в котором метастабильные атомы гелия проходили через микрометровые щели в золотой фольге. [62] [63]

В 1999 году эксперимент по квантовой интерференции (с использованием дифракционной решетки вместо двух щелей) был успешно выполнен с молекулами бакибола (каждая из которых состоит из 60 атомов углерода). [38] [64] Бакибол достаточно велик (диаметр около 0,7  нм , что почти в полмиллиона раз больше протона), чтобы его можно было увидеть в электронный микроскоп .

В 2002 году для демонстрации эксперимента с двумя щелями использовался источник полевой эмиссии электронов. В этом эксперименте когерентная электронная волна испускалась из двух близко расположенных участков эмиссии на вершине иглы, которые действовали как двойные щели, разделяя волну на две когерентные электронные волны в вакууме. Затем можно было наблюдать интерференционную картину между двумя электронными волнами. [65] В 2017 году исследователи провели эксперимент с двумя щелями, используя индуцированные светом полевые электронные эмиттеры. С помощью этой техники участки эмиссии можно оптически выбирать в масштабе десяти нанометров. Избирательно деактивируя (закрывая) один из двух источников эмиссии (щелей), исследователи смогли показать, что интерференционная картина исчезла. [66]

В 2005 году Э. Р. Элиель представил экспериментальное и теоретическое исследование оптической передачи тонкого металлического экрана, перфорированного двумя щелями субволновой длины, разделенными многими оптическими длинами волн. Показано, что общая интенсивность двухщелевой картины в дальней зоне уменьшается или увеличивается в зависимости от длины волны падающего светового пучка. [67]

В 2012 году исследователи из Университета Небраски-Линкольна провели эксперимент с двумя щелями с электронами, описанный Ричардом Фейнманом , используя новые инструменты, которые позволяли контролировать передачу двух щелей и отслеживать события обнаружения одного электрона. Электроны выстреливались электронной пушкой и проходили через одну или две щели шириной 62 нм и высотой 4 мкм. [68]

В 2013 году эксперимент по квантовой интерференции (с использованием дифракционных решеток вместо двух щелей) был успешно проведен с молекулами, каждая из которых состояла из 810 атомов (общая масса которых составляла более 10 000 атомных единиц массы ). [4] [5] Рекорд был увеличен до 2000 атомов (25 000 а.е.м.) в 2019 году. [19]

Гидродинамические пилотные волновые аналоги

Были разработаны гидродинамические аналоги , которые могут воссоздавать различные аспекты квантово-механических систем, включая одночастичную интерференцию через двойную щель. [69] Капля силиконового масла, подпрыгивая по поверхности жидкости, движется сама по себе посредством резонансных взаимодействий с собственным волновым полем. Капля мягко плещется в жидкости при каждом отскоке. В то же время рябь от прошлых отскоков влияет на ее курс. Взаимодействие капли с ее собственной рябью, которая образует то, что известно как пилотная волна , заставляет ее демонстрировать поведение, которое ранее считалось свойственным элементарным частицам, включая поведение, обычно принимаемое в качестве доказательства того, что элементарные частицы распространяются в пространстве как волны, без какого-либо определенного местоположения, пока они не будут измерены. [70] [71]

Поведение, имитируемое с помощью этой гидродинамической пилотной волновой системы, включает квантовую дифракцию одиночных частиц, [72] туннелирование, квантованные орбиты, расщепление орбитального уровня, спин и многомодальную статистику. Также возможно вывести соотношения неопределенности и принципы исключения. Доступны видео, иллюстрирующие различные особенности этой системы. (См. Внешние ссылки.)

Однако более сложные системы, включающие две или более частиц в суперпозиции, не поддаются такому простому, классически интуитивному объяснению. [73] Соответственно, гидродинамический аналог запутанности не был разработан. [69] Тем не менее, оптические аналоги возможны. [74]

Двухщелевой эксперимент по времени

В 2023 году был опубликован эксперимент по воссозданию интерференционной картины во времени путем направления импульса лазера накачки на экран, покрытый оксидом индия и олова (ITO), что изменило бы свойства электронов внутри материала из-за эффекта Керра , изменив его из прозрачного в отражающий примерно на 200 фемтосекунд, где последующий зондирующий лазерный луч, попадающий на экран ITO, затем увидел бы это временное изменение оптических свойств как щель во времени, а две из них как двойную щель с разностью фаз, складывающейся деструктивно или конструктивно на каждом компоненте частоты, что привело бы к интерференционной картине. [75] [76] [77] Аналогичные результаты были получены классическим способом на волнах на воде. [75] [77]

Классическая волновая оптическая формулировка

Картина дифракции на двух щелях с падающей плоской волной
Фотография двухщелевой интерференции солнечного света.
Две щели освещаются плоской волной, показывая разницу хода.

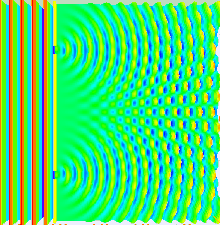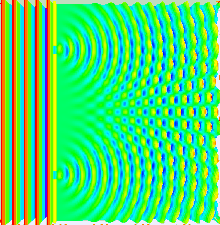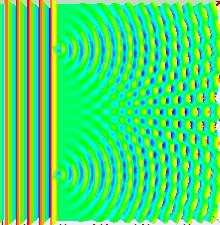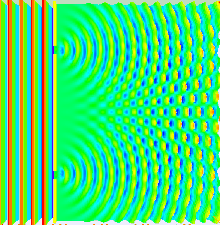
Большая часть поведения света может быть смоделирована с использованием классической волновой теории. Принцип Гюйгенса-Френеля является одной из таких моделей; он утверждает, что каждая точка на волновом фронте генерирует вторичный вейвлет, и что возмущение в любой последующей точке может быть найдено путем суммирования вкладов отдельных вейвлетов в этой точке. Это суммирование должно учитывать фазу , а также амплитуду отдельных вейвлетов. Измерить можно только интенсивность светового поля — она пропорциональна квадрату амплитуды.

В эксперименте с двумя щелями две щели освещаются квазимонохроматическим светом одного лазера. Если ширина щелей достаточно мала (намного меньше длины волны лазерного света), щели дифрагируют свет на цилиндрические волны. Эти два цилиндрических волновых фронта накладываются друг на друга, и амплитуда, а следовательно, и интенсивность, в любой точке объединенных волновых фронтов зависят как от величины, так и от фазы двух волновых фронтов. Разница в фазе между двумя волнами определяется разницей в расстоянии, пройденном двумя волнами.

Если расстояние наблюдения велико по сравнению с разделением щелей ( дальнее поле ), разность фаз можно найти, используя геометрию, показанную на рисунке ниже справа. Разность путей между двумя волнами, распространяющимися под углом θ, определяется по формуле:

Где d — расстояние между двумя щелями. Когда две волны находятся в фазе, т. е. разность хода равна целому числу длин волн, суммированная амплитуда, а следовательно, и суммированная интенсивность максимальны, а когда они находятся в противофазе, т. е. разность хода равна половине длины волны, полутора длинам волн и т. д., то две волны взаимно уничтожаются, и суммированная интенсивность равна нулю. Этот эффект известен как интерференция . Максимумы интерференционных полос возникают под углами

где λ — длина волны света. Угловое расстояние между полосами, θ f , определяется как

Расстояние между полосами на расстоянии z от щелей определяется выражением

Например, если две щели находятся на расстоянии 0,5 мм ( d ) и освещаются лазером с длиной волны 0,6 мкм ( λ ), то на расстоянии 1 м ( z ) расстояние между полосами составит 1,2 мм.

Если ширина щелей b значительна по сравнению с длиной волны, то для определения интенсивности дифрагированного света необходимо уравнение дифракции Фраунгофера следующим образом: [78]

где функция sinc определяется как sinc( x ) = sin( x )/ x для x ≠ 0, и sinc(0) = 1.

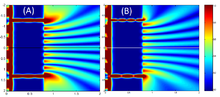
Это проиллюстрировано на рисунке выше, где первый рисунок представляет собой картину дифракции одной щели, заданную функцией sinc в этом уравнении, а второй рисунок показывает объединенную интенсивность света, дифрагированного от двух щелей, где функция cos представляет тонкую структуру, а более грубая структура представляет дифракцию на отдельных щелях, как описано функцией sinc .

Аналогичные расчеты для ближнего поля можно выполнить, применив уравнение дифракции Френеля , которое подразумевает, что по мере приближения плоскости наблюдения к плоскости, в которой расположены щели, дифракционные картины, связанные с каждой щелью, уменьшаются в размерах, так что область, в которой происходит интерференция, уменьшается и может вообще исчезнуть, когда нет перекрытия двух дифракционных картин. [79]

Формулировка интеграла по траектории

Один из бесконечного числа равновероятных путей, используемых в интеграле путей Фейнмана (см. также: Винеровский процесс )

Двухщелевой эксперимент может проиллюстрировать формулировку интеграла по траектории квантовой механики, предложенную Фейнманом. [80] Формулировка интеграла по траектории заменяет классическое понятие единственной, уникальной траектории для системы суммой по всем возможным траекториям. Траектории складываются с помощью функционального интегрирования .

Каждый путь считается одинаково вероятным и, таким образом, вносит одинаковый вклад. Однако фаза этого вклада в любой заданной точке пути определяется действием вдоль пути:

Затем все эти вклады суммируются, а величина конечного результата возводится в квадрат , чтобы получить распределение вероятностей для положения частицы:

Как всегда бывает при вычислении вероятности , результаты необходимо нормализовать , наложив:

Распределение вероятностей результата представляет собой нормализованный квадрат нормы суперпозиции , по всем путям от точки происхождения до конечной точки, волн, распространяющихся пропорционально действию вдоль каждого пути. Различия в кумулятивном действии вдоль различных путей (и, следовательно, относительные фазы вкладов) создают интерференционную картину, наблюдаемую в двухщелевом эксперименте. Фейнман подчеркивал, что его формулировка является всего лишь математическим описанием, а не попыткой описать реальный процесс, который мы можем измерить.

Интерпретации эксперимента

Как и мысленный эксперимент с котом Шредингера , эксперимент с двумя щелями часто используется для того, чтобы подчеркнуть различия и сходства между различными интерпретациями квантовой механики .

Стандартная квантовая физика

Стандартная интерпретация эксперимента с двумя щелями заключается в том, что паттерн представляет собой волновое явление, представляющее собой интерференцию между двумя амплитудами вероятности, по одной для каждой щели. Эксперименты с низкой интенсивностью показывают, что паттерн заполняется при обнаружении одной частицы за раз. Любое изменение в аппарате, предназначенном для обнаружения частицы в определенной щели, изменяет амплитуды вероятности, и интерференция исчезает. [50] : S298  Эта интерпретация не зависит от любого сознательного наблюдателя. [81] :  S281 

Взаимодополняемость

Нильс Бор интерпретировал квантовые эксперименты, такие как эксперимент с двумя щелями, используя концепцию дополнительности. [82] По мнению Бора, квантовые системы не являются классическими, но измерения могут давать только классические результаты. Определенные пары классических свойств никогда не будут наблюдаться в квантовой системе одновременно: интерференционная картина волн в эксперименте с двумя щелями исчезнет, ​​если частицы будут обнаружены на щелях. Современные версии количественные версии концепции допускают непрерывный компромисс между видимостью интерференционных полос и вероятностью обнаружения частицы на щели. [83] [84]

Копенгагенская интерпретация

Копенгагенская интерпретация представляет собой совокупность взглядов на значение квантовой механики , вытекающих из работ Нильса Бора , Вернера Гейзенберга , Макса Борна и других. Термин «Копенгагенская интерпретация», по-видимому, был придуман Гейзенбергом в 1950-х годах для обозначения идей, разработанных в период 1925–1927 годов, сглаживая его разногласия с Бором. [82] [85] [86] [87] Следовательно, нет окончательного исторического утверждения о том, что влечет за собой интерпретация. К общим чертам версий Копенгагенской интерпретации относятся идея о том, что квантовая механика по своей сути недетерминирована , с вероятностями, вычисляемыми с использованием правила Борна , и некоторой формы принципа дополнительности . [88] : 41–54  Более того, акт «наблюдения» или «измерения» объекта необратим, и никакая истина не может быть приписана объекту, кроме как в соответствии с результатами его измерения . В копенгагенской интерпретации дополнительность означает, что конкретный эксперимент может продемонстрировать поведение частицы (прохождение через определенную щель) или поведение волны (интерференцию), но не оба одновременно. [88] :  49  [89] [90] В копенгагенской интерпретации вопрос о том, через какую щель проходит частица, не имеет смысла, если нет детектора. [91] [92]

Реляционная интерпретация

Согласно реляционной интерпретации квантовой механики , впервые предложенной Карло Ровелли , [93] наблюдения, такие как в эксперименте с двумя щелями, являются результатом взаимодействия между наблюдателем (измерительным устройством) и наблюдаемым (физически взаимодействующим) объектом, а не какого-либо абсолютного свойства, которым обладает объект. В случае электрона, если он изначально «наблюдается» в определенной щели, то взаимодействие наблюдатель–частица (фотон–электрон) включает информацию о положении электрона. Это частично ограничивает возможное местоположение частицы на экране. Если она «наблюдается» (измеряется с помощью фотона) не в определенной щели, а на экране, то нет никакой информации о «каком пути» как части взаимодействия, поэтому «наблюдаемое» положение электрона на экране определяется строго его функцией вероятности. Это делает результирующий рисунок на экране таким же, как если бы каждый отдельный электрон прошел через обе щели. [ необходима цитата ]

Многомировая интерпретация

Как и в случае с Копенгагеном, существует несколько вариантов многомировой интерпретации . Объединяющей темой является то, что физическая реальность отождествляется с волновой функцией, и эта волновая функция всегда развивается унитарно, т. е. следуя уравнению Шредингера без коллапсов. [94] [95] Следовательно, существует множество параллельных вселенных, которые взаимодействуют друг с другом только посредством интерференции. Дэвид Дойч утверждает, что способ понять эксперимент с двумя щелями заключается в том, что в каждой вселенной частица проходит через определенную щель, но на ее движение влияет интерференция с частицами в других вселенных. Это создает наблюдаемые полосы. [96] Дэвид Уоллес, другой сторонник многомировой интерпретации, пишет, что в знакомой установке двухщелевого эксперимента два пути недостаточно разделены, чтобы описание в терминах параллельных вселенных имело смысл. [97]

Теория де Бройля–Бома

Альтернатива стандартному пониманию квантовой механики, теория де Бройля-Бома утверждает, что частицы также имеют точное местоположение в любое время, и что их скорости определяются волновой функцией. Таким образом, в то время как отдельная частица будет проходить через одну конкретную щель в двухщелевом эксперименте, так называемая «пилотная волна», которая влияет на нее, будет проходить через обе. Двухщелевые траектории де Бройля-Бома были впервые рассчитаны Крисом Дьюдни во время работы с Крисом Филиппидисом и Бэзилом Хайли в Биркбекском колледже (Лондон). [98] Теория де Бройля-Бома дает те же статистические результаты, что и стандартная квантовая механика, но обходится без многих ее концептуальных трудностей, добавляя сложность посредством специального квантового потенциала для управления частицами. [99]

Хотя эта модель во многом похожа на уравнение Шредингера , известно, что она не работает в релятивистских случаях [100] и не учитывает такие особенности, как рождение или уничтожение частиц в квантовой теории поля . Многие авторы, такие как лауреаты Нобелевской премии Вернер Гейзенберг [101] , сэр Энтони Джеймс Леггетт [102] и сэр Роджер Пенроуз [103], критиковали ее за то, что она не добавляет ничего нового.

Появились более сложные варианты этого типа подхода, например, трехволновая гипотеза [104] [105] Рышарда Городецкого, а также другие сложные комбинации волн де Бройля и Комптона. [106] [107] [108] На сегодняшний день нет никаких доказательств того, что они полезны.

Бомовские траектории

Смотрите также

Ссылки

  1. ^ Янг, Томас (1804). «Бейкеровская лекция. Эксперименты и вычисления относительно физической оптики». Philosophical Transactions of the Royal Society of London . 94 : 1–16. doi : 10.1098/rstl.1804.0001 . S2CID  110408369.
  2. ^ Наварро, Жауме (2010). «Дифракция электронов у Томсона: ранние отклики на квантовую физику в Британии». Британский журнал истории науки . 43 (2): 245–275. doi :10.1017/S0007087410000026. ISSN  0007-0874. S2CID  171025814.
  3. ^ Томсон, ГП; Рид, А. (1927). «Дифракция катодных лучей на тонкой пленке». Nature . 119 (3007): 890. Bibcode :1927Natur.119Q.890T. doi : 10.1038/119890a0 . ISSN  0028-0836. S2CID  4122313.
  4. ^ ab "Физики бьют рекорды в области корпускулярно-волнового дуализма"
  5. ^ ab Eibenberger, Sandra; et al. (2013). «Интерференция материальных волн с частицами, выбранными из молекулярной библиотеки с массами, превышающими 10000 а.е.м.». Physical Chemistry Chemical Physics . 15 (35): 14696–14700. arXiv : 1310.8343 . Bibcode :2013PCCP...1514696E. doi :10.1039/C3CP51500A. PMID  23900710. S2CID  3944699.
  6. ^ Хотя нет сомнений в том, что демонстрация Юнгом оптической интерференции с использованием солнечного света, отверстий и карточек сыграла важную роль в принятии волновой теории света, существуют некоторые сомнения относительно того, проводил ли он когда-либо на самом деле эксперимент по двухщелевой интерференции.
    • Робинсон, Эндрю (2006). Последний человек, который знал всё. Нью-Йорк, Нью-Йорк: Pi Press. С. 123–124. ISBN 978-0-13-134304-7.
  7. ^ Кипнис, Наум С. (1991). История принципа интерференции света. Springer. стр. 65. ISBN 978-0-8176-2316-6.
  8. ^ ab Lederman, Leon M.; Christopher T. Hill (2011). Квантовая физика для поэтов. США: Prometheus Books. стр. 102–111. ISBN 978-1-61614-281-0.
  9. ^ abcdef Фейнман, Ричард П.; Роберт Б. Лейтон; Мэтью Сэндс (1965). Лекции Фейнмана по физике, т. 3. Эддисон-Уэсли. стр. 1.1–1.8. ISBN 978-0-201-02118-9.
  10. ^ Фейнман, 1965, стр. 1.5
  11. ^ Дарлинг, Дэвид (2007). «Волново-корпускулярный дуализм». Интернет-энциклопедия науки . Миры Дэвида Дарлинга . Получено 18 октября 2008 г.
  12. ^ Фейнман, 1965, стр. 1.7
  13. ^ Леон Ледерман; Кристофер Т. Хилл (27 сентября 2011 г.). Квантовая физика для поэтов. Prometheus Books, Publishers. стр. 109. ISBN 978-1-61614-281-0.
  14. ^ " ...если в двухщелевом эксперименте детекторы, регистрирующие выходящие фотоны, размещаются сразу за диафрагмой с двумя щелями: Фотон регистрируется в одном детекторе, а не в обоих... " Мюллер-Кирстен, Х. Дж. В. (2006). Введение в квантовую механику: уравнение Шредингера и интеграл по траектории. США: World Scientific. стр. 14. ISBN 978-981-2566911.
  15. ^ Плотницкий, Аркадий (2012). Нильс Бор и дополнительность: Введение. США: Springer. С. 75–76. ISBN 978-1-4614-4517-3.
  16. ^ " Кажется, что свет проходит через одну щель или другую в форме фотонов, если мы поставим эксперимент, чтобы определить, через какую щель проходит фотон, но проходит через обе щели в форме волны, если мы проведем эксперимент по интерференции " . Rae, Alastair IM (2004). Квантовая физика: иллюзия или реальность?. Великобритания: Cambridge University Press. стр. 9–10. ISBN 978-1-139-45527-5.
  17. ^ Фейнман, Фейнмановские лекции по физике , 3 : Квантовая механика, стр. 1-1 «Однако есть один счастливый случай — электроны ведут себя точно так же, как свет».
  18. ↑ См.: Эксперимент Дэвиссона–Джермера Дэвиссон, К. Дж. (1928). «Дифракция электронов на кристалле никеля». Bell System Technical Journal . 7 : 90–105. doi :10.1002/j.1538-7305.1928.tb00342.x.
  19. ^ ab Яаков Й. Фейн; Филипп Гейер; Патрик Цвик; Филип Киалка; Себастьян Педалино; Марсель Майор; Стефан Герлих; Маркус Арндт (сентябрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа». Nature Physics . 15 (12): 1242–1245. Bibcode :2019NatPh..15.1242F. doi :10.1038/s41567-019-0663-9. S2CID  203638258.
  20. ^ Чарльз Сандерс Пирс первым предложил использовать этот эффект в качестве независимого от артефактов эталона длины.
    • CS Peirce (июль 1879 г.). «Заметка о ходе экспериментов по сравнению длины волны с измерителем». American Journal of Science , на который ссылается Crease, Robert P. (2011). World in the Balance: The historic quest for an absolute system of measurement . New York: WW Norton. стр. 317. ISBN 978-0-393-07298-3 . стр. 203. 
  21. ^ Грин, Брайан (1999). Элегантная Вселенная: Суперструны, Скрытые Измерения и Поиски Окончательной Теории. Нью-Йорк: WW Norton. С. 97–109. ISBN 978-0-393-04688-5.
  22. ^ Фейнман, 1965, глава 3
  23. ^ Сэр Джеффри, Ингрэм Тейлор (1909). «Интерференционные полосы со слабым светом». Проф. к. фил. общ . 15 : 114.
  24. ^ Йонссон, Клаус (1 августа 1961 г.). «Электронные помехи и лучшие художественные работы». Zeitschrift für Physik (на немецком языке). 161 (4): 454–474. Бибкод : 1961ZPhy..161..454J. дои : 10.1007/BF01342460. ISSN  0044-3328. S2CID  121659705.
  25. ^ Йонссон, Клаус (1 января 1974 г.). «Дифракция электронов на нескольких щелях». American Journal of Physics . 42 (1): 4–11. Bibcode : 1974AmJPh..42....4J. doi : 10.1119/1.1987592. ISSN  0002-9505.
  26. ^ Мерли, ПГ; Миссироли, ГФ; Поцци, Г (1976). «О статистическом аспекте явлений электронной интерференции». American Journal of Physics . 44 (3): 306–307. Bibcode : 1976AmJPh..44..306M. doi : 10.1119/1.10184.
  27. ^ Роза, Р. (2012). «Эксперимент Мерли–Миссироли–Поцци с двухщелевой электронной интерференцией». Physics in Perspective . 14 (2): 178–194. Bibcode : 2012PhP....14..178R. doi : 10.1007/s00016-011-0079-0. PMC 4617474. PMID  26525832 . 
  28. ^ "Самый красивый эксперимент". Physics World 2002 Архивировано 24 мая 2021 г. на Wayback Machine
  29. ^ Стидс, Джон; Мерли, Пьер Джорджио; Поцци, Джулио; Миссироли, ДжанФранко; Тономура, Акира (2003). «Двущелевой эксперимент с одиночными электронами». Мир физики . 16 (5): 20–21. дои : 10.1088/2058-7058/16/5/24. ISSN  0953-8585.
  30. ^ Фраббони, Стефано; Габриэлли, Алессандро; Карло Газзади, Джиан; Джорджи, Филиппо; Маттеуччи, Джорджио; Поцци, Джулио; Чезари, Никола Семприни; Вилла, Мауро; Зокколи, Антонио (май 2012 г.). «Эксперимент Янга-Фейнмана с двумя щелями с одиночными электронами: построение интерференционной картины и распределения времени прибытия с использованием пиксельного детектора с быстрым считыванием». Ультрамикроскопия . 116 : 73–76. doi :10.1016/j.ultramic.2012.03.017. ISSN  0304-3991.
  31. ^ Коули, Дж. М. (1995). Физика дифракции . Персональная библиотека Северной Голландии (3-е изд.). Амстердам: Elsevier. ISBN 978-0-444-82218-5.
  32. ^ Спенс, Джон CH (2017). Высокоразрешающая электронная микроскопия (Четвертое издание, впервые опубликовано в мягкой обложке). Оксфорд: Oxford University Press. ISBN 978-0-19-879583-4.
  33. ^ Сала, С.; Арига, А.; Эредитато, А.; Феррагут, Р.; Джаммарки, М.; Леоне, М.; Пистилло, К.; Скамполи, П. (2019). «Первая демонстрация волновой интерферометрии антивещества». Достижения науки . 5 (5): eaav7610. Бибкод : 2019SciA....5.7610S. doi : 10.1126/sciadv.aav7610. ПМК 6499593 . ПМИД  31058223. 
  34. ^ Бах, Роджер; Поуп, Дамиан; Лиу, Си-Хванг; Бателан, Герман (13 марта 2013 г.). "Управляемая двухщелевая электронная дифракция". New Journal of Physics . 15 (3). IOP Publishing: 033018. arXiv : 1210.6243 . Bibcode : 2013NJPh...15c3018B. doi : 10.1088/1367-2630/15/3/033018. ISSN  1367-2630. S2CID  832961.
  35. ^ Грин, Брайан (2007). Ткань космоса: пространство, время и текстура реальности. Random House LLC. стр. 90. ISBN 978-0-307-42853-0.
  36. ^ Анантасвами, Анил (2018). Через две двери одновременно: элегантный эксперимент, который раскрывает загадку нашей квантовой реальности . Penguin. стр. 63. ISBN 978-1-101-98611-0.
  37. ^ Донати, О.; Миссироли, Г.Ф.; Поцци, Г. (1973). «Эксперимент по электронной интерференции». Американский журнал физики . 41 (5): 639–644. Bibcode : 1973AmJPh..41..639D. doi : 10.1119/1.1987321.
  38. ^ ab New Scientist: Квантовые чудеса: Корпускулы и бакиболы, 2010 (Введение, для полного текста необходима подписка, цитируется полностью в [1] Архивировано 25 сентября 2017 г. в Wayback Machine )
  39. ^ Корпускулярно-волновой дуализм C60 Архивировано 31 марта 2012 г. на Wayback Machine
  40. ^ Nairz, Olaf; Brezger, Björn; Arndt, Markus; Zeilinger, Anton (2001). "Дифракция сложных молекул на структурах, сделанных из света". Phys. Rev. Lett . 87 (16): 160401. arXiv : quant-ph/0110012 . Bibcode :2001PhRvL..87p0401N. doi :10.1103/physrevlett.87.160401. PMID  11690188. S2CID  21547361.
  41. ^ Nairz, O; Arndt, M; Zeilinger, A (2003). "Quantum interference experimental with large oxygen" (PDF) . American Journal of Physics . 71 (4): 319–325. Bibcode :2003AmJPh..71..319N. doi :10.1119/1.1531580. Архивировано из оригинала (PDF) 4 июня 2015 г. . Получено 4 июня 2015 г. .
  42. ^ Стефан Герлих и др. (5 апреля 2011 г.). «Квантовая интерференция больших органических молекул». Nature Communications . 2 : 263. Bibcode : 2011NatCo ... 2..263G. doi : 10.1038/ncomms1263. PMC 3104521. PMID  21468015. 
  43. ^ Яаков Фейн и др. (декабрь 2019 г.). «Квантовая суперпозиция молекул за пределами 25 кДа». Nature Physics . 15 (12): 1242–1245. Bibcode :2019NatPh..15.1242F. doi :10.1038/s41567-019-0663-9. S2CID  203638258.
  44. ^ Хессмо, Б., М. В. Митчелл и П. Уолтер. «Запутанные фотоны демонстрируют интерференцию и билокацию». CERN Courier (2004): 11.
  45. ^ Ведрал, Влатко (2006). Введение в квантовую информатику . Oxford University Press. ISBN 978-0-19-921570-6. OCLC  442351498.
  46. ^ Харрисон, Дэвид (2002). «Комплементарность и копенгагенская интерпретация квантовой механики». UPSCALE . Кафедра физики, Университет Торонто . Получено 21 июня 2008 г.
  47. ^ Кэссиди, Дэвид (2008). «Квантовая механика 1925–1927: Триумф Копенгагенской интерпретации». Вернер Гейзенберг . Американский институт физики. Архивировано из оригинала 14 января 2016 года . Получено 21 июня 2008 года .
  48. ^ Boscá Díaz-Pintado, María C. (29–31 марта 2007 г.). «Обновление корпускулярно-волнового дуализма». 15-я конференция Великобритании и Европы по основам физики . Лидс, Великобритания . Получено 21 июня 2008 г.
  49. ^ Бартелл, Л. (1980). «Взаимодополняемость в эксперименте с двумя щелями: о простых реализуемых системах для наблюдения промежуточного поведения частиц и волн». Physical Review D. 21 ( 6): 1698–1699. Bibcode : 1980PhRvD..21.1698B. doi : 10.1103/PhysRevD.21.1698.
  50. ^ ab Zeilinger, A. (1999). «Эксперимент и основы квантовой физики». Reviews of Modern Physics . 71 (2): S288–S297. Bibcode :1999RvMPS..71..288Z. doi :10.1103/RevModPhys.71.S288.
  51. ^ P. Mittelstaedt; A. Prieur; R. Schieder (1987). "Unsharp корпускулярно-волновой дуализм в эксперименте с расщепленным пучком фотонов". Foundations of Physics . 17 (9): 891–903. Bibcode : 1987FoPh...17..891M. doi : 10.1007/BF00734319. S2CID  122856271.
  52. ^ Д. М. Гринбергер и А. Ясин, «Одновременное знание волн и частиц в нейтронном интерферометре», Physics Letters A 128 , 391–4 (1988).
  53. ^ Сен, Д. (2014). «Соотношения неопределенности в квантовой механике». Current Science . 107 (2): 203–218. ISSN  0011-3891. JSTOR  24103129.«Однако, «компромисс волна-частица» теперь выражается в терминах неравенства, известного как дуальность Энглерта-Гринбергера или просто отношение дуальности волна-частица». См. также ссылку 24 в этой работе.
  54. ^ ab Hillmer, R.; Kwiat, P. (2007). «Самодельный квантовый ластик». Scientific American . Том 296, № 5. С. 90–95. Bibcode : 2007SciAm.296e..90H. doi : 10.1038/scientificamerican0507-90 . Получено 11 января 2016 г.
  55. ^ ab Chiao, RY; PG Kwiat; Steinberg, AM (1995). «Квантовая нелокальность в двухфотонных экспериментах в Беркли». Квантовая и полуклассическая оптика: Журнал Европейского оптического общества, часть B. 7 ( 3): 259–278. arXiv : quant-ph/9501016 . Bibcode : 1995QuSOp...7..259C. doi : 10.1088/1355-5111/7/3/006. S2CID  118987962.
  56. ^ Фрэнсис, Мэтью (21 мая 2012 г.). «Распутывание корпускулярно-волнового дуализма в эксперименте с двумя щелями». Ars Technica .
  57. ^ ab Свенссон, Бенгт EY (2013). «Педагогический обзор квантовой теории измерений с упором на слабые измерения». Quanta . 2 (1): 18–49. arXiv : 1202.5148 . doi :10.12743/quanta.v2i1.12. S2CID  119242577.
  58. ^ Пфлейгор, Р. Л.; Мандель, Л. (июль 1967 г.). «Интерференция независимых фотонных пучков». Physical Review . 159 (5): 1084–1088. Bibcode :1967PhRv..159.1084P. doi :10.1103/PhysRev.159.1084.
  59. ^ "Интерференция независимых фотонных пучков: эксперимент Пфлегора-Манделя". Архивировано из оригинала 3 января 2011 г. Получено 16 июня 2011 г.>
  60. ^ Силлитто, Р. М.; Уайкс, Кэтрин (1972). «Эксперимент по интерференции со световыми лучами, модулированными в противофазе электрооптическим затвором». Physics Letters A. 39 ( 4): 333–334. Bibcode : 1972PhLA...39..333S. doi : 10.1016/0375-9601(72)91015-8.
  61. ^ ""К легкой частице"".
  62. ^ Carnal, O.; Mlynek, J. (май 1991). «Двухщелевой эксперимент Юнга с атомами: простой атомный интерферометр». Physical Review Letters . 66 (21): 2689–2694. Bibcode :1991PhRvL..66.2689C. doi :10.1103/PhysRevLett.66.2689. PMID  10043591.
  63. ^ Carnal, O.; Mlynek, J. (1991). «Двухщелевой эксперимент Юнга с атомами: простой атомный интерферометр». Physical Review Letters . 66 (21): 2689–2692. Bibcode :1991PhRvL..66.2689C. doi :10.1103/PhysRevLett.66.2689. PMID  10043591 . Получено 20 марта 2022 г. .>
  64. ^ Арндт, Маркус; Наирз, Олаф; Вос-Андреа, Джулиан; Келлер, Клаудия; Ван дер Зув, Гербранд; Цайлингер, Антон (1999). «Волново-частичный дуализм молекул C60». Природа . 401 (6754): 680–682. Бибкод : 1999Natur.401..680A. дои : 10.1038/44348. PMID  18494170. S2CID  4424892.
  65. ^ Ошима, К.; Мастуда, К.; Кона, Т.; Могами, Ю.; Комаки, М.; Мурата, Ю.; Ямашита, Т.; Кузумаки, Т.; Хориике, Ю. (4 января 2002 г.). "Интерференция электронов Юнга в моделях полевой эмиссии". Physical Review Letters . 88 (3): 038301. Bibcode :2002PhRvL..88c8301O. doi :10.1103/PhysRevLett.88.038301. ISSN  0031-9007. PMID  11801091.
  66. ^ Янагисава, Хирофуми; Чаппина, Марсело; Хафнер, Кристиан; Шец, Йоханнес; Остервальдер, Юрг; Клинг, Матиас Ф. (4 октября 2017 г.). «Оптическое управление двухщелевым интерферометром Янга для лазерно-индуцированной эмиссии электронов из нано-иглы». Научные отчеты . 7 (1): 12661. arXiv : 1710.02216 . Бибкод : 2017NatSR...712661Y. дои : 10.1038/s41598-017-12832-3. ISSN  2045-2322. ПМЦ 5627254 . ПМИД  28978914. 
  67. ^ Схоутен, ХФ; Кузьмин Н.; Дюбуа, Ж.; Виссер, Т.Д.; Гбур, Г. ; Алкемаде, ПФА; Блок, Х.; Хофт, ГВ; Ленстра, Д.; Элиэль, ER (7 февраля 2005 г.). «Двущелевая передача с плазмоном: новый взгляд на эксперимент Янга». Физ. Преподобный Летт . 94 (5): 053901. Бибкод : 2005PhRvL..94e3901S. doi : 10.1103/physrevlett.94.053901. hdl : 1887/71482 . PMID  15783641. S2CID  19197175.
  68. ^ Бах, Роджер и др. (март 2013 г.). "Управляемая двухщелевая дифракция электронов". New Journal of Physics . 15 (3): 033018. arXiv : 1210.6243 . Bibcode : 2013NJPh...15c3018B. doi : 10.1088/1367-2630/15/3/033018. S2CID  832961.
  69. ^ ab Bush, John WM (2015). "Pilot-wave hydrodynamics" (PDF) . Annual Review of Fluid Mechanics . 47 (1): 269–292. Bibcode :2015AnRFM..47..269B. doi :10.1146/annurev-fluid-010814-014506. hdl : 1721.1/89790 . Архивировано (PDF) из оригинала 21 июня 2015 г. . Получено 21 июня 2015 г. .
  70. ^ Буш, Джон ВМ (2010). «Квантовая механика, написанная в большом формате». PNAS . 107 (41): 17455–17456. Bibcode : 2010PNAS..10717455B. doi : 10.1073/pnas.1012399107 . PMC 2955131 . 
  71. ^ Натали Вулховер (30 июня 2014 г.). «Мы все это время неправильно интерпретировали квантовую механику?». Wired .
  72. ^ Couder, Y.; Fort, E. (2012). «Вероятности и траектории в классическом корпускулярно-волновом дуализме». Journal of Physics: Conference Series . 361 (1): 012001. Bibcode : 2012JPhCS.361a2001C. doi : 10.1088/1742-6596/361/1/012001 .
  73. ^ Багготт, Джим (2011). Квантовая история: история за 40 мгновений . Нью-Йорк: Oxford University Press. стр. 76. («Волновая функция системы, содержащей N частиц, зависит от 3 N координат положения и является функцией в 3 N -мерном конфигурационном пространстве или «фазовом пространстве». Трудно визуализировать реальность, содержащую мнимые функции в абстрактном многомерном пространстве. Однако никаких трудностей не возникает, если мнимым функциям не давать реальной интерпретации».)
  74. ^ Ли, Пэнъюнь; Сан, Ифань; Ян, Чжэньвэй; Сун, Синьбин; Чжан, Сяндун (2016). «Классическая гиперкорреляция и волновая оптическая аналогия квантового сверхплотного кодирования». Scientific Reports . 5 : 18574. Bibcode :2015NatSR...518574L. doi :10.1038/srep18574. PMC 4686973 . PMID  26689679. 
  75. ^ ab Bacot, Vincent; Labousse, Matthieu; Eddi, Antonin; Fink, Mathias; Fort, Emmanuel (ноябрь 2016 г.). «Обращение времени и голография с пространственно-временными преобразованиями». Nature Physics . 12 (10): 972–977. arXiv : 1510.01277 . Bibcode :2016NatPh..12..972B. doi :10.1038/nphys3810. ISSN  1745-2481. S2CID  53536274.
  76. ↑ Родригес-Фортуньо, Франсиско Х. (3 апреля 2023 г.). «Оптический двухщелевой эксперимент во времени». Физика природы . 19 (7): 929–930. Бибкод : 2023NatPh..19..929R. дои : 10.1038/s41567-023-02026-2. ISSN  1745-2481. S2CID  257945438.
  77. ^ ab Castelvecchi, Davide (3 апреля 2023 г.). «Световые волны, протиснувшиеся через „щели во времени“». Nature . 616 (7956): 230. Bibcode :2023Natur.616..230C. doi :10.1038/d41586-023-00968-4. PMID  37012471. S2CID  257922697.
  78. ^ Дженкинс ФА и Уайт ХЕ, Основы оптики, 1967, Макгроу Хилл, Нью-Йорк
  79. ^ Лонгхерст RS, Физическая и геометрическая оптика, 1967, 2-е издание, Longmans
  80. ^ Зи, Энтони (2010). Квантовая теория поля в двух словах (2-е изд.). Princeton University Press. С. 2–16. ISBN 978-0-691-14034-6.
  81. ^ Mandel, L. (1 марта 1999 г.). «Квантовые эффекты в однофотонной и двухфотонной интерференции». Reviews of Modern Physics . 71 (2): S274–S282. doi :10.1103/RevModPhys.71.S274. ISSN  0034-6861.
  82. ^ ab Faye, Jan (2019). «Копенгагенская интерпретация квантовой механики». В Zalta, Edward N. (ред.). Стэнфордская энциклопедия философии . Исследовательская лаборатория метафизики, Стэнфордский университет.
  83. ^ Wootters, William K.; Zurek, Wojciech H. (15 января 1979 г.). «Комплементарность в двухщелевом эксперименте: квантовая неразделимость и количественное утверждение принципа Бора». Physical Review D. 19 ( 2): 473–484. doi :10.1103/PhysRevD.19.473. ISSN  0556-2821.
  84. ^ Бартелл, Л.С. (15 марта 1980 г.). «Комплементарность в эксперименте с двумя щелями: о простых реализуемых системах для наблюдения промежуточного поведения частиц и волн». Physical Review D. 21 ( 6): 1698–1699. doi :10.1103/PhysRevD.21.1698. ISSN  0556-2821.
  85. ^ Camilleri, K.; Schlosshauer, M. (2015). «Нильс Бор как философ эксперимента: бросает ли теория декогеренции вызов учению Бора о классических концепциях?». Исследования по истории и философии современной физики . 49 : 73–83. arXiv : 1502.06547 . Bibcode : 2015SHPMP..49...73C. doi : 10.1016/j.shpsb.2015.01.005. S2CID  27697360.
  86. ^ Шайбе, Эрхард (1973). Логический анализ квантовой механики . Pergamon Press. ISBN 978-0-08-017158-6. OCLC  799397091. [T]Нет смысла искать Копенгагенскую интерпретацию как единую и последовательную логическую структуру. Такие термины, как «Копенгагенская интерпретация» или «Копенгагенская школа», основаны на истории развития квантовой механики; они образуют упрощенный и часто удобный способ ссылки на идеи ряда физиков, сыгравших важную роль в становлении квантовой механики и сотрудничавших с Бором в его Институте или принимавших участие в дискуссиях в решающие годы. При более внимательном рассмотрении довольно легко увидеть, что эти идеи расходятся в деталях и что, в частности, взгляды Бора, духовного лидера школы, образуют отдельную сущность, которую теперь можно понять только путем тщательного изучения как можно большего числа соответствующих публикаций самого Бора.
  87. ^ Mermin, N. David (1 января 2017 г.). «Почему QBism не является копенгагенской интерпретацией и что Джон Белл мог подумать об этом». В Bertlmann, Reinhold; Zeilinger, Anton (ред.). Quantum [Un]Speakables II . The Frontiers Collection. Springer International Publishing. стр. 83–93. arXiv : 1409.2454 . doi :10.1007/978-3-319-38987-5_4. ISBN 978-3-319-38985-1. S2CID  118458259.
  88. ^ ab Omnès, Roland (1999). "Копенгагенская интерпретация". Understanding Quantum Mechanics . Princeton University Press. doi :10.2307/j.ctv173f2pm.9. S2CID  203390914.
  89. ^ Розенфельд, Л. (1953). «Спор о дополнительности». Science Progress (1933–) . 41 (163): 393–410. ISSN  0036-8504. JSTOR  43414997.
  90. ^ Перес, Эшер (1995). Квантовая теория: концепции и методы . Kluwer Academic Publishers. стр. 36–39. ISBN 0-7923-2549-4.
  91. ^ Омнес, Р. (1994). Интерпретация квантовой механики . Princeton University Press. стр. 167. ISBN 978-0-691-03669-4. OCLC  439453957.
  92. ^ Брукнер, Часлав ; Цайлингер, Антон (2005). «Квантовая физика как наука об информации». В Elitzur, Авшалом С.; Долев, Шахар; Коленда, Нэнси (ред.). Quo Vadis Quantum Mechanics?. Берлин, Гейдельберг: Springer. стр. 47–61. doi :10.1007/3-540-26669-0_3. ISBN 978-3-540-22188-3.
  93. ^ Ровелли, Карло (1996). «Реляционная квантовая механика». Международный журнал теоретической физики . 35 (8): 1637–1678. arXiv : quant-ph/9609002 . Bibcode :1996IJTP...35.1637R. doi :10.1007/BF02302261. S2CID  16325959.
  94. ^ Кент, Адриан (февраль 2015 г.). «Имеет ли смысл говорить о самолокализации неопределенности в универсальной волновой функции? Замечания о Себенсе и Кэрролле». Основы физики . 45 (2): 211–217. arXiv : 1408.1944 . Bibcode : 2015FoPh...45..211K. doi : 10.1007/s10701-014-9862-5. ISSN  0015-9018. S2CID  118471198.
  95. ^ Вайдман, Лев (5 августа 2021 г.). «Многомировая интерпретация квантовой механики». В Zalta, Edward N. (ред.). Стэнфордская энциклопедия философии .
  96. ^ Дойч, Дэвид (1998). Ткань реальности. Лондон: Penguin. С. 40–53. ISBN 978-0-14-014690-5.
  97. ^ Уоллес, Дэвид (2012). Возникающая мультивселенная . Оксфорд: Oxford University Press. стр. 382. ISBN 978-0-19-954696-1.
  98. ^ Philippidis, C.; Dewdney, C.; Hiley, BJ (1979). «Квантовая интерференция и квантовый потенциал». Il Nuovo Cimento B. 52 ( 1): 15–28. Bibcode : 1979NCimB..52...15P. doi : 10.1007/bf02743566. ISSN  1826-9877. S2CID  53575967.
  99. ^ "Бомовская механика". Стэнфордская энциклопедия философии . Лаборатория метафизических исследований, Стэнфордский университет. 2017.
  100. ^ Goldstein, Sheldon (2021), «Бомовская механика», в Zalta, Edward N. (ред.), The Stanford Encyclopedia of Philosophy (ред. осень 2021 г.), Metaphysics Research Lab, Stanford University , получено 14 августа 2023 г.
  101. ^ Гейзенберг, В. (1956). Паули, В. (ред.). « Нильс Бор и развитие физики: очерки, посвященные Нильсу Бору по случаю его семидесятилетия ». Physics Today . 9 (8): 12. doi :10.1063/1.3060063. ISSN  0031-9228.
  102. ^ Леггетт, А. Дж. (2002). «Проверка пределов квантовой механики: мотивация, состояние дел, перспективы». Журнал физики: конденсированное вещество . 14 (15): R415–R451. doi :10.1088/0953-8984/14/15/201. ISSN  0953-8984. S2CID  250911999.
  103. ^ Пенроуз, Роджер (2004). Дорога к реальности: Полное руководство по законам Вселенной. Лондон: Cape. ISBN 978-0-224-04447-9.
  104. ^ Horodecki, R. (1981). «Волна де Бройля и ее двойная волна». Physics Letters A. 87 ( 3): 95–97. Bibcode : 1981PhLA...87...95H. doi : 10.1016/0375-9601(81)90571-5. ISSN  0375-9601.
  105. ^ Городецкий, Р. (1983). «Сверхсветовая сингулярная двойная волна». Lettere al Nuovo Cimento . 36 (15): 509–511. дои : 10.1007/bf02817964. ISSN  1827-613X. S2CID  120784358.
  106. ^ Das, SN (1984). «Волна де Бройля и волна Комптона». Physics Letters A. 102 ( 8): 338–339. Bibcode : 1984PhLA..102..338D. doi : 10.1016/0375-9601(84)90291-3. ISSN  0375-9601.
  107. ^ Mukhopadhyay, P. (1986). «Корреляция между длиной волны Комптона и длиной волны де Бройля». Physics Letters A. 114 ( 4): 179–182. Bibcode : 1986PhLA..114..179M. doi : 10.1016/0375-9601(86)90200-8. ISSN  0375-9601.
  108. ^ Elbaz, Claude (1985). «О волнах де Бройля и волнах Комптона массивных частиц». Physics Letters A. 109 ( 1–2): 7–8. Bibcode : 1985PhLA..109....7E. doi : 10.1016/0375-9601(85)90379-2. ISSN  0375-9601.

Дальнейшее чтение

Внешние ссылки

На Викискладе есть медиафайлы по теме «Эксперименты с двумя щелями» .

Интерактивная анимация

Эксперименты с отдельными частицами

Гидродинамический аналог

Компьютерное моделирование