Угол

Фигура, образованная двумя лучами, встречающимися в общей точке

Зеленый угол, образованный двумя красными лучами в декартовой системе координат.

В евклидовой геометрии угол — это фигура, образованная двумя лучами , называемыми сторонами угла, имеющими общую конечную точку, называемую вершиной угла. ^[1] Углы, образованные двумя лучами, также известны как плоские углы, поскольку они лежат в плоскости , содержащей лучи. Углы также образуются пересечением двух плоскостей; они называются двугранными углами . Две пересекающиеся кривые также могут определять угол, который является углом лучей, лежащих по касательной к соответствующим кривым в точке их пересечения.

Величина угла называется угловой мерой или просто «углом». Угол поворота — это мера, условно определяемая как отношение длины дуги окружности к ее радиусу , и может быть отрицательным числом . В случае геометрического угла дуга центрирована в вершине и ограничена сторонами. В случае поворота дуга центрирована в центре поворота и ограничена любой другой точкой, а ее изображение — поворотом.

История и этимология

Слово angle происходит от латинского слова angulus , означающего «угол». Родственные слова включают греческое ἀγκύλος ( ankylοs ), означающее «кривой, изогнутый», и английское слово « ankle ». Оба связаны с протоиндоевропейским корнем *ank- , означающим «сгибать» или «лук». ^[2]

Евклид определяет плоский угол как наклон друг к другу, в плоскости, двух линий, которые встречаются друг с другом и не лежат прямо друг относительно друга. Согласно неоплатоническому метафизику Проклу , угол должен быть либо качеством, либо количеством, либо отношением. Первое понятие, угол как качество, использовал Эвдем Родосский , который рассматривал угол как отклонение от прямой линии ; второе, угол как качество, Карп Антиохийский , который рассматривал его как интервал или пространство между пересекающимися линиями; Евклид принял третье: угол как отношение. ^[3]

Определение углов

В математических выражениях принято использовать греческие буквы ( α , β , γ , θ , φ , . . . ) в качестве переменных, обозначающих размер некоторого угла ^[4] (символ π обычно не используется для этой цели, чтобы избежать путаницы с константой, обозначаемой этим символом ). Также используются строчные латинские буквы ( a ,  b ,  c , . . . ). В контекстах, где это не вызывает путаницы, угол может быть обозначен заглавной римской буквой, обозначающей его вершину. Примеры см. на рисунках в этой статье.

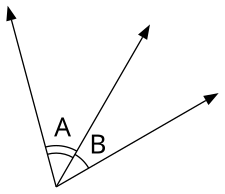
Три определяющие точки могут также определять углы в геометрических фигурах. Например, угол с вершиной A, образованный лучами AB и AC (то есть полупрямыми из точки A через точки B и C), обозначается ∠BAC или . Если нет риска путаницы, угол иногда может обозначаться только одной вершиной (в данном случае «угол A»). ${\displaystyle {\widehat {\rm {BAC}}}}$

Другими словами, угол, обозначенный, скажем, как ∠BAC, может относиться к любому из четырех углов: углу по часовой стрелке от B до C относительно A, углу против часовой стрелки от B до C относительно A, углу по часовой стрелке от C до B относительно A или углу против часовой стрелки от C до B относительно A, где направление, в котором измеряется угол, определяет его знак (см. § Знаковые углы ). Однако во многих геометрических ситуациях из контекста очевидно, что подразумевается положительный угол, меньший или равный 180 градусам, и в этих случаях не возникает никакой двусмысленности. В противном случае, чтобы избежать двусмысленности, могут быть приняты определенные соглашения, так что, например, ∠BAC всегда относится к углу против часовой стрелки (положительному) от B до C относительно A, а ∠CAB — к углу против часовой стрелки (положительному) от C до B относительно A.

Типы

Отдельные углы

Существует некоторая общая терминология для углов, мера которых всегда неотрицательна (см. § Знаковые углы ):

• Угол, равный 0° или не повернутый, называется нулевым углом . ^[5]
• Угол, меньший прямого угла (менее 90°), называется острым углом ^[6] («acute» означает « острый »).
• Угол, равный ⁠1/4⁠  поворот (90° или ⁠π/2⁠ радианы) называется прямым углом . Две линии, образующие прямой угол, называются нормальными , ортогональными или перпендикулярными . ^[7]
• Угол, больший прямого угла и меньший развернутого угла (между 90° и 180°), называется тупым углом ^[6] («тупой» означает «тупой»).
• Угол, равный ⁠1/2⁠  поворот (180° или π радиан) называется прямым углом . ^[5]
• Угол, больший прямого угла, но меньший одного оборота (между 180° и 360°), называется углом отражения .
• Угол, равный 1 обороту (360° или 2π радианам ), называется полным углом , полным углом , круглым углом или перигоном .
• Угол, не кратный прямому углу, называется косым углом .

Названия, интервалы и единицы измерения приведены в таблице ниже:

Вертикальные и.mw-parser-output .vanchor>:target~.vanchor-text{background-color:#b1d2ff}@media screen{html.skin-theme-clientpref-night .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}@media screen and (prefers-color-scheme:dark){html.skin-theme-clientpref-os .mw-parser-output .vanchor>:target~.vanchor-text{background-color:#0f4dc9}}соседнийпары углов

Углы A и B — пара вертикальных углов; углы C и D — пара вертикальных углов. Штриховка здесь используется для обозначения равенства углов.

При пересечении двух прямых в одной точке образуются четыре угла. Попарно эти углы называются в соответствии с их расположением относительно друг друга.

• Пара углов, расположенных друг напротив друга, образованных двумя пересекающимися прямыми линиями, которые образуют форму, подобную букве «X», называются вертикальными углами или противолежащими углами или вертикально противолежащими углами . Их сокращенно обозначают как vert. opp. ∠s . ^[8]

  Равенство вертикально противоположных углов называется теоремой о вертикальном угле . Эвдем Родосский приписал доказательство Фалесу Милетскому . ^{[9] [10]} Предложение показало, что поскольку оба из пары вертикальных углов являются дополнительными к обоим смежным углам, вертикальные углы равны по мере. Согласно исторической заметке, ^[10] когда Фалес посетил Египет, он заметил, что всякий раз, когда египтяне рисовали две пересекающиеся линии, они измеряли вертикальные углы, чтобы убедиться, что они равны. Фалес пришел к выводу, что можно доказать, что все вертикальные углы равны, если принять некоторые общие понятия, такие как:

  • Все прямые углы равны.
  • Равные, сложенные с равными, равны.
  • Равные вычтены из равных и равны.

  Когда два смежных угла образуют прямую линию, они являются дополнительными. Поэтому, если мы предположим, что мера угла A равна x , мера угла C будет равна 180° − x . Аналогично, мера угла D будет равна 180° − x . Оба угла C и D имеют меры, равные 180 ° − x , и являются конгруэнтными. Поскольку угол B является дополнительным к обоим углам C и D , любую из этих мер углов можно использовать для определения меры угла B. Используя меру либо угла C , либо угла D , мы находим, что мера угла B равна 180° − (180° − x ) = 180° − 180° + x = x . Следовательно, оба угла A и B имеют меры, равные x , и равны по мере.

  

  Углы А и В смежные.

• Смежные углы , часто сокращенно обозначаемые как adj. ∠s , — это углы, которые имеют общую вершину и ребро, но не имеют общих внутренних точек. Другими словами, это углы, стоящие рядом или смежные, имеющие общую «руку». Смежные углы, сумма которых составляет прямой угол, развернутый угол или полный угол, являются особыми и соответственно называются дополнительными , добавочными и дополнительными углами (см. § Объединение пар углов ниже).

Трансверсаль — это линия, которая пересекает пару (часто параллельных) линий и связана с внешними углами , внутренними углами , накрест лежащими внешними углами , накрест лежащими внутренними углами , соответствующими углами и последовательными внутренними углами . ^[11]

Объединение пар углов

Постулат сложения углов гласит, что если B находится внутри угла AOC, то

$${\displaystyle m\angle \mathrm {AOC} =m\angle \mathrm {AOB} +m\angle \mathrm {BOC} }$$

То есть, величина угла AOC равна сумме величины угла AOB и величины угла BOC.

Три специальные пары углов предполагают суммирование углов:

Дополнительные углы a и b ( b является дополнением к a , а a является дополнением к b ) .

• Дополнительные углы — это пары углов, сумма мер которых составляет один прямой угол ( ⁠1/4⁠ поворот, 90°, или ⁠π/2⁠ радиан). ^[12] Если два дополнительных угла смежны, их неразделенные стороны образуют прямой угол. В евклидовой геометрии два острых угла в прямоугольном треугольнике являются дополнительными, поскольку сумма внутренних углов треугольника составляет 180 градусов, а прямой угол составляет 90 градусов.

  Прилагательное дополняющий происходит от латинского слова completum , связанного с глаголом complere , «заполнять». Острый угол «заполняется» его дополнением, образуя прямой угол.

  Разница между углом и прямым углом называется дополнением угла. ^[13]

  Если углы A и B являются дополнительными, то справедливы следующие соотношения: $${\displaystyle {\begin{aligned}&\sin ^{2}A+\sin ^{2}B=1&&\cos ^{2}A+\cos ^{2}B=1\\[3pt]&\tan A=\cot B&&\sec A=\csc B\end{aligned}}}$$

  ( Тангенс угла равен котангенсу его дополнения, а его секанс равен косекансу его дополнения.)

  Приставка « ко- » в названиях некоторых тригонометрических соотношений относится к слову «дополнительный».

  

  Углы a и b являются дополнительными углами.

• Два угла, которые в сумме дают развернутый угол ( ⁠1/2⁠ поворот, 180° или π радиан) называются дополнительными углами . ^[14]

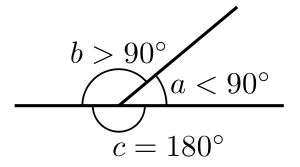
  Если два дополнительных угла являются смежными (т. е. имеют общую вершину и делят только одну сторону), их неразделенные стороны образуют прямую линию . Такие углы называются линейной парой углов . ^[15] Однако дополнительные углы не обязательно должны находиться на одной линии и могут быть разделены в пространстве. Например, смежные углы параллелограмма являются дополнительными, а противолежащие углы вписанного четырехугольника (четырехугольника, все вершины которого лежат на одной окружности) являются дополнительными.

  Если точка P является внешней по отношению к окружности с центром O и если касательные из P касаются окружности в точках T и Q, то ∠TPQ и ∠TOQ являются дополнительными.

  Синусы смежных углов равны. Их косинусы и тангенсы (если не определено) равны по величине, но имеют противоположные знаки.

  В евклидовой геометрии любая сумма двух углов треугольника является дополнительной к третьему, поскольку сумма внутренних углов треугольника является прямым углом.

  

  Углы AOB и COD сопряжены, так как образуют полный угол. Учитывая величины, 45° + 315° = 360°.

• Два угла, которые в сумме дают полный угол (1 оборот, 360° или 2π радиан ), называются дополнительными углами или сопряженными углами . ^[16]

  Разница между углом и полным углом называется выражением угла или сопряжением угла.

Углы, связанные с многоугольниками

Внутренние и внешние углы

• Угол, являющийся частью простого многоугольника, называется внутренним углом , если он лежит внутри этого простого многоугольника. Простой вогнутый многоугольник имеет по крайней мере один внутренний угол, то есть отражённый угол.
  В евклидовой геометрии сумма внутренних углов треугольника составляет π радиан , 180° или ⁠1/2⁠ поворот; меры внутренних углов простого выпуклого четырехугольника в сумме составляют 2 π радиан, 360° или 1 поворот. В общем случае меры внутренних углов простого выпуклого многоугольника с n сторонами в сумме составляют ( n  − 2) π  радиан, или ( n  − 2)180 градусов, ( n  − 2)2 прямых угла, или ( n  − 2) ⁠1/2⁠  очередь.
• Дополнение внутреннего угла называется внешним углом ; то есть внутренний угол и внешний угол образуют линейную пару углов. В каждой вершине многоугольника есть два внешних угла, каждый из которых определяется путем расширения одной из двух сторон многоугольника, которые встречаются в вершине; эти два угла вертикальны и, следовательно, равны. Внешний угол измеряет величину поворота, которую необходимо сделать в вершине, чтобы проследить многоугольник. ^[17] Если соответствующий внутренний угол является углом отражения, внешний угол следует считать отрицательным . Даже в непростом многоугольнике может быть возможно определить внешний угол. Тем не менее, придется выбрать ориентацию плоскости (или поверхности ) , чтобы определить знак меры внешнего угла.
  В евклидовой геометрии сумма внешних углов простого выпуклого многоугольника, если только один из двух внешних углов предполагается в каждой вершине, будет равна одному полному обороту (360°). Внешний угол здесь можно назвать дополнительным внешним углом . Внешние углы обычно используются в программах Logo Turtle при рисовании правильных многоугольников.
• В треугольнике биссектрисы двух внешних углов и биссектриса другого внутреннего угла пересекаются в одной точке. ^[18] : ¹⁴⁹
• В треугольнике три точки пересечения, каждая из которых является внешней биссектрисой угла с противолежащей продолженной стороной , лежат на одной прямой . ^{[18] : 149}
• В треугольнике три точки пересечения, две из которых находятся между биссектрисой внутреннего угла и противолежащей стороной, а третья — между биссектрисой другого внешнего угла и продолженной противолежащей стороной, лежат на одной прямой. ^{[18] : 149}
• Некоторые авторы используют название « внешний угол простого многоугольника» для обозначения внешнего угла, дополняющего внутренний угол ( а не дополнительного!). ^[19] Это противоречит приведенному выше использованию.

Углы, связанные с плоскостью

• Угол между двумя плоскостями (например, двумя смежными гранями многогранника ) называется двугранным углом . ^[13] Его можно определить как острый угол между двумя прямыми, перпендикулярными плоскостям.
• Угол между плоскостью и пересекающей ее прямой равен девяноста градусам минус угол между пересекающей прямой и прямой, проходящей через точку пересечения и перпендикулярной плоскости.

Измерение углов

Размер геометрического угла обычно характеризуется величиной наименьшего поворота, который отображает один из лучей в другой. Углы одинакового размера называются равными конгруэнтными или равными по мере .

В некоторых контекстах, таких как определение точки на окружности или описание ориентации объекта в двух измерениях относительно опорной ориентации, углы, которые отличаются на точное кратное полного оборота, фактически эквивалентны. В других контекстах, таких как определение точки на спиральной кривой или описание кумулятивного вращения объекта в двух измерениях относительно опорной ориентации, углы, которые отличаются на ненулевое кратное полного оборота, не эквивалентны.

Мера угла θ равна ⁠с/г⁠ радианы .

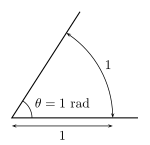
Для измерения угла θ чертится дуга окружности с центром в вершине угла, например, с помощью циркуля . Отношение длины дуги s к радиусу окружности r равно числу радиан в угле: ^[20] Традиционно в математике и СИ радиан считается равным безразмерной единице 1, поэтому обычно опускается. $${\displaystyle \theta ={\frac {s}{r}}\,\mathrm {rad} .}$$

Угол, выраженный другой угловой единицей, может быть получен путем умножения угла на подходящую константу преобразования вида ⁠к/2π​⁠ , где k — мера полного поворота, выраженная в выбранных единицах (например, k = 360° для градусов или 400 град для градианов ):

$${\displaystyle \theta ={\frac {k}{2\pi }}\cdot {\frac {s}{r}}.}$$

Значение θ, определенное таким образом, не зависит от размера окружности: если длина радиуса изменяется, то длина дуги изменяется в той же пропорции, поэтому отношение s / r остается неизменным. ^{[nb 1]}

Единицы

Определение 1 радиана

На протяжении всей истории углы измерялись в различных единицах . Они известны как угловые единицы , при этом наиболее современными единицами являются градус (°), радиан (рад) и град (град), хотя на протяжении всей истории использовались и многие другие . ^[22] Большинство единиц измерения углов определяются таким образом, что один оборот (т. е. угол, охватываемый окружностью круга в его центре) равен n единицам для некоторого целого числа n . Двумя исключениями являются радиан (и его десятичные дольные) и часть диаметра.

В Международной системе величин угол определяется как безразмерная величина, и в частности, радиан является безразмерной единицей. Эта конвенция влияет на то, как углы рассматриваются в размерном анализе .

В следующей таблице перечислены некоторые единицы измерения углов.

Анализ размеров

Плоский угол можно определить как θ = s / r , где θ - (числовое значение) противолежащего угла в радианах, s - длина дуги, а r - радиус. Один радиан СИ соответствует (числовому значению) угла, выраженного в радианах, для которого s = r , следовательно, 1 радиан СИ = 1 м/м = 1. ^[28] Однако рад следует использовать только для выражения углов, а не для выражения отношений длин в целом. ^[29] Аналогичный расчет с использованием площади кругового сектора θ = 2 A / r ² дает 1 радиан СИ как 1 м ² /м ² = 1. ^[30] Ключевым фактом является то, что радиан СИ - это безразмерная единица , равная 1 . В SI 2019 радиан СИ определяется соответственно как 1 рад = 1 . ^[31] В математике и во всех областях науки давно принято использовать рад = 1. [ ^{32] [33]}

Джакомо Прандо пишет: «Нынешнее положение дел неизбежно приводит к призрачным появлениям и исчезновениям радиана в размерном анализе физических уравнений». ^[34] Например, объект, подвешенный на веревке к блоку, поднимется или опустится на y = rθ сантиметров, где r — числовое значение радиуса блока, выраженное в сантиметрах, а θ — числовое значение угла, на который поворачивается блок, выраженное в радианах. При умножении r на θ единица радиан не появляется в результате. Аналогично в формуле для угловой скорости катящегося колеса, ω = v / r , радианы появляются в единицах ω , но не в правой части. ^[35] Энтони Френч называет это явление «вечной проблемой в преподавании механики». ^[36] Оберхофер говорит, что типичный совет игнорировать радианы во время размерного анализа и добавлять или удалять радианы в единицах в соответствии с соглашением и контекстными знаниями «педагогически неудовлетворителен». ^[37]

В 1993 году Метрический комитет Американской ассоциации учителей физики указал, что радиан должен явно появляться в величинах только тогда, когда при использовании других мер угла будут получены другие числовые значения, например, в величинах меры угла (рад), угловой скорости (рад/с), углового ускорения (рад/с2 ⁾ и крутильной жесткости (Н⋅м/рад), а не в величинах крутящего момента (Н⋅м) и углового момента (кг⋅м2 ^/ с). ^[38]

По крайней мере, дюжина ученых между 1936 и 2022 годами вносили предложения рассматривать радиан как базовую единицу измерения для базовой величины (и размерности) «плоского угла». ^{[39] [40] [41]} Обзор предложений Куинси выделяет два класса предложений. Первый вариант изменяет единицу радиуса на метры на радиан, но это несовместимо с размерным анализом для площади круга , π r ² . Другой вариант — ввести размерную константу. По словам Куинси, этот подход «логически строг» по сравнению с СИ, но требует «модификации многих знакомых математических и физических уравнений». ^[42] Размерная константа для угла «довольно странная», и сложность модификации уравнений для добавления размерной константы, вероятно, исключит ее широкое использование. ^[41]

В частности, Куинси идентифицирует предложение Торренса ввести константу η, равную 1 обратному радиану (1 рад ⁻¹ ), аналогично введению константы ε0 . ^{[42] [a]} С этим изменением формула для угла, противолежащего центру окружности, s = rθ , изменяется так, чтобы стать s = ηrθ , а ряд Тейлора для синуса угла θ _{становится} : ^{[41] [43]} где — числовое значение угла, выраженное в радианах. Заглавная функция Sin — это «полная» функция, которая принимает аргумент с размерностью угла и не зависит от выраженных единиц, ^[43] в то время как sin — это традиционная функция на чистых числах , которая предполагает, что ее аргумент — безразмерное число в радианах. ^[44] Заглавный символ может быть обозначен, если ясно, что подразумевается полная форма. ^{[41] [45]} $${\displaystyle \operatorname {Sin} \theta =\sin \ x=x-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\cdots =\eta \theta -{\frac {(\eta \theta )^{3}}{3!}}+{\frac {(\eta \theta )^{5}}{5!}}-{\frac {(\eta \theta )^{7}}{7!}}+\cdots ,}$$ ${\displaystyle x=\eta \theta =\theta /{\text{rad}}}$ ${\displaystyle \operatorname {Sin} }$ ${\displaystyle \sin }$

Текущая система СИ может рассматриваться относительно этой структуры как естественная система единиц , где предполагается, что выполняется уравнение η = 1 , или, аналогично, 1 рад = 1. Это соглашение о радианах позволяет опускать η в математических формулах. ^[46]

Определение радиана в качестве базовой единицы может быть полезным для программного обеспечения, где недостаток длинных уравнений минимален. ^[47] Например, библиотека единиц Boost определяет единицы измерения угла с plane_angleразмерностью, ^[48] а система единиц Mathematica аналогичным образом рассматривает углы как имеющие размерность угла. ^{[49] [50]}

Знаковые углы

При измерении от оси x углы на единичной окружности считаются положительными в направлении против часовой стрелки и отрицательными в направлении по часовой стрелке .

Часто бывает полезно ввести соглашение, которое позволяет положительным и отрицательным угловым значениям представлять ориентации и/или вращения в противоположных направлениях или «смыслах» относительно некоторой точки отсчета.

В двумерной декартовой системе координат угол обычно определяется двумя сторонами, с вершиной в начале координат. Начальная сторона находится на положительной оси x , в то время как другая сторона или конечная сторона определяется мерой от начальной стороны в радианах, градусах или поворотах, причем положительные углы представляют повороты к положительной оси y , а отрицательные углы представляют повороты к отрицательной оси y . Когда декартовы координаты представлены стандартным положением , определяемым осью x вправо и осью y вверх, положительные повороты происходят против часовой стрелки , а отрицательные циклы — по часовой стрелке .

Во многих контекстах угол − θ фактически эквивалентен углу «один полный оборот минус θ ». Например, ориентация, представленная как −45°, фактически равна ориентации, определенной как 360° − 45° или 315°. Хотя конечное положение одинаково, физическое вращение (движение) на −45° не то же самое, что вращение на 315° (например, вращение человека, держащего метлу, покоящуюся на пыльном полу, оставит визуально разные следы подметенных областей на полу).

В трехмерной геометрии понятия «по часовой стрелке» и «против часовой стрелки» не имеют абсолютного значения, поэтому направление положительных и отрицательных углов должно определяться через ориентацию , которая обычно определяется нормальным вектором, проходящим через вершину угла и перпендикулярным плоскости, в которой лежат лучи угла.

В навигации пеленги или азимуты измеряются относительно севера. По соглашению, если смотреть сверху, углы пеленга положительны по часовой стрелке, поэтому пеленг 45 ° соответствует северо-восточной ориентации. Отрицательные пеленги не используются в навигации, поэтому северо-западная ориентация соответствует пеленгу 315°.

Эквивалентные углы

• Углы, имеющие одинаковую меру (т. е. одинаковую величину), называются равными или конгруэнтными . Угол определяется своей мерой и не зависит от длин сторон угла (например, все прямые углы имеют одинаковую меру).
• Два угла, которые имеют общие конечные стороны, но отличаются по размеру на целое число оборотов, называются котерминальными углами .
• Опорный угол (иногда называемый связанным углом ) для любого угла θ в стандартном положении — это положительный острый угол между конечной стороной θ и осью x (положительной или отрицательной). ^{[51] [52] Процедурно величина опорного угла для данного угла может быть определена путем взятия} модуля величины угла ⁠1/2⁠ поворот, 180°, или π радиан, затем остановка, если угол острый, в противном случае взятие дополнительного угла, 180° минус уменьшенная величина. Например, угол в 30 градусов уже является опорным углом, а угол в 150 градусов также имеет опорный угол в 30 градусов (180° − 150°). Углы в 210° и 510° также соответствуют опорному углу в 30 градусов (210° mod 180° = 30°, 510° mod 180° = 150°, дополнительный угол которого равен 30°).

Связанные величины

Для угловой единицы определяющим является то, что постулат сложения углов выполняется. Некоторые величины, связанные с углами, для которых постулат сложения углов не выполняется, включают:

• Наклон или градиент равен тангенсу угла ; градиент часто выражается в процентах. Для очень малых значений (менее 5% ) наклон линии приблизительно равен измерению в радианах ее угла с горизонтальным направлением.
• Расстояние между двумя линиями определяется в рациональной геометрии как квадрат синуса угла между линиями. Поскольку синус угла и синус его дополнительного угла одинаковы, любой угол поворота, который отображает одну из линий в другую, приводит к тому же значению расстояния между линиями .
• Хотя это и делается редко, можно сообщить прямые результаты тригонометрических функций , таких как синус угла.

Углы между кривыми

Угол между двумя кривыми в точке P определяется как угол между касательными A и B в точке P.

Угол между прямой и кривой (смешанный угол) или между двумя пересекающимися кривыми (криволинейный угол) определяется как угол между касательными в точке пересечения. Различные названия (сейчас редко, если вообще когда-либо, используемые) были даны частным случаям: — амфициртовый (греч. ἀμφί , с обеих сторон, κυρτός, выпуклый) или циссоидальный (греч. κισσός, плющ), двояковыпуклый; ксистроидальный или систроидальный (греч. ξυστρίς, инструмент для соскабливания), вогнуто-выпуклый; амфициоловый (греч. κοίλη, впадина) или angulus lunularis , двояковогнутый. ^[53]

Биссекция и трисекция углов

Древнегреческие математики знали, как разделить угол пополам (на два угла равной меры), используя только циркуль и линейку , но могли сделать трисекцию только для некоторых углов. В 1837 году Пьер Ванцель показал, что это построение невозможно выполнить для большинства углов.

Скалярное произведение и обобщения

В евклидовом пространстве угол θ между двумя евклидовыми векторами u и v связан с их скалярным произведением и их длинами формулой

$${\displaystyle \mathbf {u} \cdot \mathbf {v} =\cos(\theta )\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.}$$

Эта формула предоставляет простой метод нахождения угла между двумя плоскостями (или криволинейными поверхностями) по их нормальным векторам и между скрещивающимися прямыми по их векторным уравнениям.

Внутренний продукт

Чтобы определить углы в абстрактном реальном пространстве скалярного произведения , мы заменяем евклидово скалярное произведение ( · ) скалярным произведением , т.е. ${\displaystyle \langle \cdot ,\cdot \rangle }$

$${\displaystyle \langle \mathbf {u} ,\mathbf {v} \rangle =\cos(\theta )\ \left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.}$$

В комплексном внутреннем пространстве произведения выражение для косинуса выше может давать недействительные значения, поэтому оно заменяется на

$${\displaystyle \operatorname {Re} \left(\langle \mathbf {u} ,\mathbf {v} \rangle \right)=\cos(\theta )\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.}$$

или, что более распространено, с использованием абсолютного значения, с

$${\displaystyle \left|\langle \mathbf {u} ,\mathbf {v} \rangle \right|=\left|\cos(\theta )\right|\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|.}$$

Последнее определение игнорирует направление векторов. Таким образом, оно описывает угол между одномерными подпространствами и , охватываемый векторами и соответственно. ${\displaystyle \operatorname {span} (\mathbf {u} )}$ ${\displaystyle \operatorname {span} (\mathbf {v} )}$ ${\displaystyle \mathbf {u} }$ ${\displaystyle \mathbf {v} }$

Углы между подпространствами

Определение угла между одномерными подпространствами и задается формулой ${\displaystyle \operatorname {span} (\mathbf {u} )}$ ${\displaystyle \operatorname {span} (\mathbf {v} )}$

$${\displaystyle \left|\langle \mathbf {u} ,\mathbf {v} \rangle \right|=\left|\cos(\theta )\right|\left\|\mathbf {u} \right\|\left\|\mathbf {v} \right\|}$$

в гильбертовом пространстве может быть расширено до подпространств конечных размерностей. При наличии двух подпространств , с , это приводит к определению углов, называемых каноническими или главными углами между подпространствами. ${\displaystyle {\mathcal {U}}}$ ${\displaystyle {\mathcal {W}}}$ ${\displaystyle \dim({\mathcal {U}}):=k\leq \dim({\mathcal {W}}):=l}$ ${\displaystyle k}$

Углы в римановой геометрии

В римановой геометрии метрический тензор используется для определения угла между двумя касательными . Где U и V — касательные векторы, а g _ij — компоненты метрического тензора G ,

$${\displaystyle \cos \theta ={\frac {g_{ij}U^{i}V^{j}}{\sqrt {\left|g_{ij}U^{i}U^{j}\right|\left|g_{ij}V^{i}V^{j}\right|}}}.}$$

Гиперболический угол

Гиперболический угол является аргументом гиперболической функции, так же как круговой угол является аргументом круговой функции . Сравнение можно визуализировать как размер отверстий гиперболического сектора и кругового сектора , поскольку площади этих секторов соответствуют величинам углов в каждом случае. ^[54] В отличие от кругового угла, гиперболический угол неограничен. Когда круговые и гиперболические функции рассматриваются как бесконечные ряды по их угловому аргументу, круговые являются просто чередующимися формами рядов гиперболических функций. Это сравнение двух рядов, соответствующих функциям углов, было описано Леонардом Эйлером во Введении в анализ бесконечного (1748).

Углы в географии и астрономии

В географии местоположение любой точки на Земле может быть определено с помощью географической системы координат . Эта система определяет широту и долготу любого местоположения в терминах углов, опирающихся на центр Земли, используя экватор и (обычно) Гринвичский меридиан в качестве точек отсчета.

В астрономии заданная точка на небесной сфере (то есть видимое положение астрономического объекта) может быть идентифицирована с использованием любой из нескольких астрономических систем координат , где ссылки различаются в зависимости от конкретной системы. Астрономы измеряют угловое расстояние между двумя звездами , представляя две линии, проходящие через центр Земли , каждая из которых пересекает одну из звезд. Угол между этими линиями и угловое расстояние между двумя звездами могут быть измерены.

И в географии , и в астрономии направление визирования может быть указано в виде вертикального угла, например , высоты относительно горизонта , а также азимута относительно севера .

Астрономы также измеряют видимый размер объектов как угловой диаметр . Например, полная Луна имеет угловой диаметр приблизительно 0,5° при наблюдении с Земли. Можно сказать, «Диаметр Луны стягивает угол в полградуса». Формула малого угла может преобразовать такое угловое измерение в отношение расстояния к размеру.

Другие астрономические приближения включают в себя:

• 0,5° — приблизительный диаметр Солнца и Луны , наблюдаемый с Земли.
• 1° — приблизительная ширина мизинца на расстоянии вытянутой руки.
• 10° — приблизительная ширина сжатого кулака на расстоянии вытянутой руки.
• 20° — приблизительная ширина размаха руки на расстоянии вытянутой руки.

Эти измерения зависят от конкретного человека, и приведенные выше данные следует рассматривать только как грубые приблизительные данные .

В астрономии прямое восхождение и склонение обычно измеряются в угловых единицах, выраженных во времени, исходя из 24-часового цикла суток.

Смотрите также

• Прибор для измерения угла
• Углы между плоскостями
• Угловая статистика ( среднее значение , стандартное отклонение )
• Биссектриса угла
• Угловое ускорение
• Угловой диаметр
• Угловая скорость
• Аргумент (комплексный анализ)
• Астрологический аспект
• Центральный угол
• Проблема угла часов
• Десятичные градусы
• Двугранный угол
• Теорема о внешнем угле
• Золотой угол
• Расстояние по дуге большого круга
• Угол наклона рога
• Вписанный угол
• Иррациональный угол
• Фаза (волны)
• Транспортир
• Телесный угол
• Сферический угол
• Трансцендентный угол
• Трисекция
• Угол зенита

Примечания

1. Этот подход требует, однако, дополнительного доказательства того, что мера угла не меняется с изменением радиуса r , в дополнение к вопросу о «выбранных единицах измерения». Более гладкий подход заключается в измерении угла длиной соответствующей единичной дуги окружности. Здесь «единица» может быть выбрана безразмерной в том смысле, что это действительное число 1, связанное с единичным сегментом на действительной прямой. См., например, Radoslav M. Dimitrić. ^[21]

1. Другие предложения включают сокращение «rad» (Brinsmade 1936), обозначение (Romain 1962) и константы ם (Brownstein 1997), ◁ (Lévy-Leblond 1998), k (Foster 2010), θ _C (Quincey 2021) и (Mohr et al. 2022). ${\displaystyle \langle \theta \rangle }$ ${\displaystyle {\cal {C}}={\frac {2\pi }{\Theta }}}$

Ссылки

1. Сидоров 2001
2. Слокум 2007
3. Чисхолм 1911; Хейберг 1908, стр. 177–178.
4. Абоухантус 2010, стр. 18.
5. Moser 1971, стр. 41.
6. Годфри и Сиддонс 1919, с. 9.
7. Мозер 1971, стр. 71.
8. Вонг и Вонг 2009, стр. 161–163
9. Евклид . Элементы .Предложение I:13.
10. Shute, Shirk & Porter 1960, стр. 25–27.
11. Якобс 1974, стр. 255.
12. "Комплементарные углы". www.mathsisfun.com . Получено 2020-08-17 .
13. Chisholm 1911
14. "Дополнительные углы". www.mathsisfun.com . Получено 2020-08-17 .
15. Якобс 1974, стр. 97.
16. Уиллис, Кларенс Эддисон (1922). Плоская геометрия. Сын Блэкистона. стр. 8.
17. Хендерсон и Таймина 2005, стр. 104.
18. Джонсон, Роджер А. Продвинутая евклидова геометрия , Dover Publications, 2007.
19. Д. Цвиллингер, ред. (1995), CRC Standard Mathematical Tables and Formulae , Бока-Ратон, Флорида: CRC Press, стр. 270как указано в Weisstein, Eric W. "Exterior Angle". MathWorld .
20. Международное бюро мер и весов (20 мая 2019 г.), Международная система единиц (СИ) (PDF) (9-е изд.), ISBN 978-92-822-2272-0, архивировано из оригинала 18 октября 2021 г.
21. Димитрич, Радослав М. (2012). «Об углах и измерениях углов» (PDF) . Преподавание математики . XV (2): 133–140. Архивировано (PDF) из оригинала 2019-01-17 . Получено 2019-08-06 .
22. "угловая единица". TheFreeDictionary.com . Получено 2020-08-31 .
23. "ooPIC Programmer's Guide - Глава 15: URCP". ooPIC Manual & Technical Specifications - ooPIC Compiler Ver 6.0 . Savage Innovations, LLC. 2007 [1997]. Архивировано из оригинала 2008-06-28 . Получено 2019-08-05 .
24. Харгривз, Шон [на польском языке] . «Углы, целые числа и модульная арифметика». blogs.msdn.com. Архивировано из оригинала 2019-06-30 . Получено 2019-08-05 .
25. Бонин, Уолтер (2016-01-11). "RE: WP-32S в 2016?". Музей HP . Архивировано из оригинала 2019-08-06 . Получено 2019-08-05 .
26. Джинс, Джеймс Хопвуд (1947). Рост физической науки. Архив CUP. стр. 7.
27. Мурнаган, Фрэнсис Доминик (1946). Аналитическая геометрия . стр. 2.
28. Международное бюро мер и весов 2019, стр. 151: «Один радиан соответствует углу, для которого s = r »
29. Международное бюро мер и весов 2019, стр. 151.
30. Куинси 2016, стр. 844: «Кроме того, как упоминается в работе Мора и Филлипса 2015, радиан можно определить через площадь A сектора ( A = ⁠1/2⁠ θ r ² ), в этом случае он имеет единицы м ² ⋅м ⁻² .
31. Международное бюро мер и весов 2019, стр. 151: «Один радиан соответствует углу, для которого s = r , таким образом, 1 рад = 1 ».
32. Международное бюро мер и весов 2019, стр. 137.
33. Бриджмен, Перси Уильямс (1922). Размерный анализ. Нью-Хейвен: Издательство Йельского университета. Угловая амплитуда качания [...] Нет размерностей.
34. Прандо, Джакомо (август 2020 г.). «Спектральная единица». Nature Physics . 16 (8): 888. Bibcode : 2020NatPh..16..888P. doi : 10.1038/s41567-020-0997-3 . S2CID  225445454.
35. Леонард, Уильям Дж. (1999). Minds-on Physics: Advanced topics in mechanics. Кендалл Хант. стр. 262. ISBN 978-0-7872-5412-4.
36. Френч, Энтони П. (май 1992 г.). «Что происходит с „радианами“? (комментарий)». The Physics Teacher . 30 (5): 260–261. doi :10.1119/1.2343535.
37. Oberhofer, ES (март 1992). «Что происходит с „радианами“?». The Physics Teacher . 30 (3): 170–171. Bibcode : 1992PhTea..30..170O. doi : 10.1119/1.2343500.
38. Aubrecht, Gordon J.; French, Anthony P.; Iona, Mario; Welch, Daniel W. (февраль 1993 г.). «Радиан — эта проблемная единица». The Physics Teacher . 31 (2): 84–87. Bibcode :1993PhTea..31...84A. doi :10.1119/1.2343667.
39. Бринсмейд 1936; Ромен 1962; Эдер 1982; Торренс 1986; Браунштейн 1997; Леви-Леблон 1998; Фостер 2010; Миллс 2016; Куинси 2021; Леонард 2021; Мор и др. 2022
40. Мор и Филлипс 2015.
41. Куинси, Пол; Браун, Ричард Дж. К. (1 июня 2016 г.). «Последствия принятия плоского угла в качестве базовой величины в СИ». Metrologia . 53 (3): 998–1002. arXiv : 1604.02373 . Bibcode :2016Metro..53..998Q. doi :10.1088/0026-1394/53/3/998. S2CID  119294905.
42. Куинси 2016.
43. Torrens 1986.
44. Мор и др. 2022, стр. 6.
45. Мор и др. 2022, стр. 8–9.
46. Куинси 2021.
47. Куинси, Пол; Браун, Ричард Дж. К. (1 августа 2017 г.). «Более четкий подход к определению систем единиц». Metrologia . 54 (4): 454–460. arXiv : 1705.03765 ​​. Bibcode :2017Metro..54..454Q. doi :10.1088/1681-7575/aa7160. S2CID  119418270.
48. Schabel, Matthias C.; Watanabe, Steven. "Boost.Units FAQ – 1.79.0". www.boost.org . Получено 5 мая 2022 г. Углы рассматриваются как единицы измерения
49. Мор и др. 2022, стр. 3.
50. "UnityDimensions—Wolfram Language Documentation". reference.wolfram.com . Получено 1 июля 2022 г. .
51. "Mathwords: Reference Angle". www.mathwords.com . Архивировано из оригинала 23 октября 2017 г. Получено 26 апреля 2018 г.
52. МакКег, Чарльз П. (2008). Тригонометрия (6-е изд.). Белмонт, Калифорния: Thomson Brooks/Cole. стр. 110. ISBN 978-0495382607.
53. Чисхолм 1911; Хейберг 1908, с. 178
54. Роберт Болдуин Хейворд (1892) Алгебра копланарных векторов и тригонометрия, глава шестая

Библиография

• Эбоугантоус, Чарльз Х. (2010), Первый курс средней школы по геометрии на евклидовой плоскости, Universal Publishers, ISBN 978-1-59942-822-2
• Бринсмейд, Дж. Б. (декабрь 1936 г.). «Плоские и телесные углы. Их педагогическая ценность при явном представлении». Американский журнал физики . 4 (4): 175–179. Bibcode : 1936AmJPh...4..175B. doi : 10.1119/1.1999110.
• Браунштейн, К. Р. (июль 1997 г.). «Углы — давайте относиться к ним прямолинейно». Американский журнал физики . 65 (7): 605–614. Bibcode : 1997AmJPh..65..605B. doi : 10.1119/1.18616 .
• Эдер, У. Э. (январь 1982 г.). «Точка зрения на величину «плоского угла»". Metrologia . 18 (1): 1–12. Бибкод : 1982Metro..18....1E. doi : 10.1088/0026-1394/18/1/002. S2CID  250750831.
• Фостер, Маркус П. (1 декабря 2010 г.). «Следующие 50 лет SI: обзор возможностей для эпохи электронной науки». Metrologia . 47 (6): R41–R51. doi :10.1088/0026-1394/47/6/R01. S2CID  117711734.
• Годфри, Чарльз; Сиддонс, AW (1919), Элементарная геометрия: практическая и теоретическая (3-е изд.), Cambridge University Press
• Хендерсон, Дэвид В.; Таймина, Дайна (2005), Опыт геометрии / евклидовой и неевклидовой с историей (3-е изд.), Pearson Prentice Hall, стр. 104, ISBN 978-0-13-143748-7
• Хейберг, Иоганн Людвиг (1908), Хит, ТЛ (ред.), Евклид, Тринадцать книг «Начал Евклида», т. 1, Кембридж : Cambridge University Press.
• Якобс, Гарольд Р. (1974), Геометрия , WH Freeman, стр. 97, 255, ISBN 978-0-7167-0456-0
• Leonard, BP (1 октября 2021 г.). «Предложение о размерно-согласованной обработке угла и телесного угла Международной системой единиц (СИ)». Metrologia . 58 (5): 052001. Bibcode :2021Metro..58e2001L. doi :10.1088/1681-7575/abe0fc. S2CID  234036217.
• Леви-Леблон, Жан-Марк (сентябрь 1998 г.). «Размерные углы и универсальные константы». American Journal of Physics . 66 (9): 814–815. Bibcode :1998AmJPh..66..814L. doi :10.1119/1.18964.
• Миллс, Ян (1 июня 2016 г.). «О единицах радиан и цикл для величины угла плоскости». Metrologia . 53 (3): 991–997. Bibcode :2016Metro..53..991M. doi :10.1088/0026-1394/53/3/991. S2CID  126032642.
• Mohr, Peter J; Phillips, William D (1 февраля 2015 г.). «Безразмерные единицы в системе СИ». Metrologia . 52 (1): 40–47. arXiv : 1409.2794 . Bibcode :2015Metro..52...40M. doi : 10.1088/0026-1394/52/1/40 .
• Mohr, Peter J; Shirley, Eric L; Phillips, William D; Trott, Michael (23 июня 2022 г.). «О размерности углов и их единицах». Metrologia . 59 (5): 053001. arXiv : 2203.12392 . Bibcode :2022Metro..59e3001M. doi : 10.1088/1681-7575/ac7bc2 .
• Мозер, Джеймс М. (1971), Современная элементарная геометрия, Prentice-Hall
• Куинси, Пол (1 апреля 2016 г.). «Диапазон вариантов обработки плоского угла и телесного угла в системе единиц». Metrologia . 53 (2): 840–845. Bibcode :2016Metro..53..840Q. doi :10.1088/0026-1394/53/2/840. S2CID  125438811.
• Куинси, Пол (1 октября 2021 г.). «Углы в системе СИ: подробное предложение по решению проблемы». Metrologia . 58 (5): 053002. arXiv : 2108.05704 . Bibcode :2021Metro..58e3002Q. doi :10.1088/1681-7575/ac023f. S2CID  236547235.
• Ромен, Жак Э. (июль 1962 г.). «Угол как четвертая фундаментальная величина». Журнал исследований Национального бюро стандартов, раздел B. 66B ( 3): 97. doi : 10.6028/jres.066B.012 .
• Сидоров, Л.А. (2001) [1994], «Угол», Энциклопедия математики , Издательство ЭМС
• Слокум, Джонатан (2007), Предварительный индоевропейский лексикон — данные Pokorny PIE, исследовательский отдел Техасского университета: центр лингвистических исследований , архивировано из оригинала 27 июня 2010 г. , извлечено 2 февраля 2010 г.
• Шут, Уильям Г.; Ширк, Уильям У.; Портер, Джордж Ф. (1960), Плоская и стереометрия , American Book Company, стр. 25–27
• Torrens, AB (1 января 1986 г.). «Об углах и угловых величинах». Metrologia . 22 (1): 1–7. Bibcode : 1986Metro..22....1T. doi : 10.1088/0026-1394/22/1/002. S2CID  250801509.
• Вонг, Так-ва; Вонг, Минг-сим (2009), «Углы пересекающихся и параллельных линий», New Century Mathematics , т. 1B (1-е изд.), Гонконг: Oxford University Press, стр. 161–163, ISBN 978-0-19-800177-5

 В этой статье использован текст из публикации, которая сейчас находится в общественном достоянии :  Чисхолм, Хью , ред. (1911), «Угол», Encyclopaedia Britannica , т. 2 (11-е изд.), Cambridge University Press, стр. 14

Внешние ссылки

• «Угол»  , Британская энциклопедия , том. 2 (9-е изд.), 1878 г., стр. 29–30.