Работа (физика)

Процесс передачи энергии объекту посредством приложения силы посредством перемещения

В науке работа — это энергия , передаваемая объекту или от него посредством приложения силы вдоль перемещения . В простейшей форме для постоянной силы, направленной по направлению движения, работа равна произведению величины силы на пройденное расстояние. Говорят, что сила совершает положительную работу , если она имеет компонент в направлении перемещения точки приложения . Сила совершает отрицательную работу , если она имеет компонент, противоположный направлению перемещения в точке приложения силы. ^[1]

Например, когда мяч удерживается над землей, а затем падает, работа, совершаемая силой тяжести, действующей на мяч при его падении, положительна и равна весу мяча (сила), умноженному на расстояние до земли (перемещение). Если мяч брошен вверх, работа, совершаемая силой тяжести, отрицательна и равна весу, умноженному на перемещение в направлении вверх.

И сила, и смещение являются векторами . Проделанная работа определяется скалярным произведением двух векторов, где результатом является скаляр . Когда сила F постоянна и угол θ между силой и смещением s также постоянен, то проделанная работа определяется по формуле: W = F s cos ⁡ θ {\displaystyle W=Fs\cos {\theta }}

Если сила переменная, то работа определяется криволинейным интегралом :

${\displaystyle W=\int {\vec {F}}\cdot d{\vec {s}}}$

где — небольшое изменение вектора смещения. ${\displaystyle d{\vec {s}}}$

Работа — скалярная величина , ^[2] поэтому она имеет только величину и не имеет направления. Работа переносит энергию из одного места в другое или из одной формы в другую. Единицей работы в системе СИ является джоуль (Дж), та же единица, что и для энергии.

История

Древнегреческое понимание физики ограничивалось статикой простых машин (балансом сил) и не включало динамику или концепцию работы. В эпоху Возрождения динамика механических сил , как называли простые машины , начала изучаться с точки зрения того, насколько далеко они могли поднять груз, в дополнение к силе, которую они могли применить, что в конечном итоге привело к новой концепции механической работы. Полная динамическая теория простых машин была разработана итальянским ученым Галилео Галилеем в 1600 году в Le Meccaniche ( О механике ), в котором он показал лежащее в основе математическое сходство машин как усилителей силы. ^{[3] [4]} Он был первым, кто объяснил, что простые машины не создают энергию, а только преобразуют ее. ^[3]

Ранние концепции работы

Хотя работа не была формально использована до 1826 года, подобные концепции существовали и до этого. Ранние названия для той же концепции включали момент активности, количество действия, скрытую живую силу, динамический эффект, эффективность и даже силу . ^[5] В 1637 году французский философ Рене Декарт писал: ^[6]

Поднятие 100 фунтов на один фут дважды равнозначно поднятию 200 фунтов на один фут или 100 фунтов на два фута.

—  Рене Декарт, Письмо Гюйгенсу

В 1686 году немецкий философ Готфрид Лейбниц писал: ^[7]

Для подъема тела А весом в 1 фунт (libra) на высоту 4 ярда (ulnae) необходима та же сила [«работа» в современных терминах], что и для подъема тела В весом в 4 фунта на высоту 1 ярд.

-  Готфрид Лейбниц, демонстрация Бревиса

В 1759 году Джон Смитон описал величину, которую он назвал «мощностью», «чтобы обозначить проявление силы, гравитации, импульса или давления, чтобы произвести движение». Смитон продолжает, что эту величину можно вычислить, если «поднятый вес умножить на высоту, на которую он может быть поднят за данное время», что делает это определение удивительно похожим на определение Кориолиса . ^[8]

Этимология

Согласно учебнику физики 1957 года Макса Джаммера , ^[9] термин работа был введен в 1826 году французским математиком Гаспаром-Гюставом Кориолисом ^[10] как «вес , поднятый на высоту», что основано на использовании ранних паровых двигателей для подъема ведер воды из затопленных рудных шахт. По словам Рене Дюга, французского инженера и историка, именно Соломону из Ко «мы обязаны термином работа в том смысле, в котором он используется в механике сейчас». ^[11]

Единицы

Единицей работы в системе СИ является джоуль (Дж), названный в честь английского физика Джеймса Прескотта Джоуля (1818-1889), который определяется как работа, необходимая для приложения силы в один ньютон при перемещении на один метр .

Размерно эквивалентный ньютон-метр (Н·м) иногда используется в качестве единицы измерения работы, но его можно спутать с единицей измерения крутящего момента . Использование Н·м не приветствуется руководством СИ , поскольку это может привести к путанице относительно того, является ли величина, выраженная в ньютон-метрах, измерением крутящего момента или измерением работы. ^[12]

Другая единица измерения работы — фут-фунт , которая происходит от английской системы измерения. Как следует из названия единицы, это произведение фунтов для единицы силы и футов для единицы перемещения. Один джоуль эквивалентен 0,07376 фут-фунта. ^[13]

Не входящие в систему СИ единицы работы включают ньютон-метр, эрг , фут-фунт, фут-фунтдаль , киловатт-час , литр-атмосферу и лошадиную силу-час . Поскольку работа имеет ту же физическую размерность , что и тепло , иногда в качестве единицы измерения используются единицы измерения, обычно предназначенные для измерения тепла или содержания энергии, такие как терм , БТЕ и калория .

Работа и энергия

Работа W, совершаемая постоянной силой величиной F в точке, которая перемещается на расстояние s по прямой в направлении действия силы, равна произведению $${\displaystyle W={\vec {F}}\cdot {\vec {s}}}$$

Например, если сила в 10 ньютонов ( F = 10 Н ) действует вдоль точки, которая перемещается на 2 метра ( s = 2 м ), то W = Fs = (10 Н) (2 м) = 20 Дж . Это приблизительно работа, совершаемая при подъеме предмета массой 1 кг с уровня земли над головой человека против силы тяжести.

Работа удваивается либо за счет подъема вдвое большего веса на то же расстояние, либо за счет подъема того же веса вдвое на то же расстояние.

Работа тесно связана с энергией . Энергия имеет ту же единицу измерения, что и работа (Джоули), поскольку энергия от объекта, совершающего работу, передается другим объектам, с которыми он взаимодействует, когда выполняется работа. ^[13] Принцип работы-энергии гласит, что увеличение кинетической энергии твердого тела вызвано равным количеством положительной работы, совершаемой над телом результирующей силой, действующей на это тело. И наоборот, уменьшение кинетической энергии вызвано равным количеством отрицательной работы, совершаемой результирующей силой. Таким образом, если чистая работа положительна, то кинетическая энергия частицы увеличивается на количество работы. Если чистая работа отрицательна, то кинетическая энергия частицы уменьшается на количество работы. ^[14]

Из второго закона Ньютона можно показать, что работа над свободным (без полей), жестким (без внутренних степеней свободы) телом равна изменению кинетической энергии E _{k ,} соответствующей линейной скорости и угловой скорости этого тела. Работа сил, создаваемых потенциальной функцией, известна как потенциальная энергия , а силы называются консервативными . Следовательно, работа над объектом, который просто перемещается в консервативном силовом поле без изменения скорости или вращения, равна минус изменению потенциальной энергии E _p объекта. Эти формулы показывают, что работа — это энергия, связанная с действием силы, поэтому работа впоследствии обладает физическими размерами и единицами энергии. Принципы работы/энергии, обсуждаемые здесь, идентичны электрическим принципам работы/энергии. $${\displaystyle W=\Delta E_{\text{k}}.}$$ $${\displaystyle W=-\Delta E_{\text{p}}.}$$

Силы ограничения

Силы ограничения определяют смещение объекта в системе, ограничивая его в пределах диапазона. Например, в случае наклона плюс гравитация объект прилипает к наклону и, будучи прикрепленным к натянутой струне, он не может двигаться в направлении наружу, чтобы сделать струну более «натянутой». Это устраняет все смещения в этом направлении, то есть скорость в направлении ограничения ограничена 0, так что силы ограничения не выполняют работу над системой.

Для механической системы ^[15] силы ограничения исключают движение в направлениях, характеризующих ограничение. Таким образом, виртуальная работа, выполняемая силами ограничения, равна нулю, что является верным только в том случае, если силы трения исключены. [ ^16]

Фиксированные, не создающие трения силы ограничения не выполняют работу над системой, ^[17] поскольку угол между движением и силами ограничения всегда равен 90° . ^[17] Примерами не создающих работу ограничений являются: жесткие взаимосвязи между частицами, скользящее движение по поверхности без трения и контакт качения без проскальзывания. ^[18]

Например, в системе блоков, такой как машина Этвуда , внутренние силы на веревке и на опорном блоке не производят никакой работы в системе. Поэтому работу нужно вычислить только для гравитационных сил, действующих на тела. Другим примером является центростремительная сила, действующая внутрь нитью на шар, совершающий равномерное круговое движение вбок, которая ограничивает движение шара по окружности, ограничивая его движение от центра окружности. Эта сила не производит никакой работы, поскольку она перпендикулярна скорости шара.

Магнитная сила, действующая на заряженную частицу, равна F = q v × B , где q — заряд, v — скорость частицы, а B — магнитное поле . Результат векторного произведения всегда перпендикулярен обоим исходным векторам, поэтому F ⊥ v . Скалярное произведение двух перпендикулярных векторов всегда равно нулю, поэтому работа W = F ⋅ v = 0 , и магнитная сила не совершает работу. Она может изменить направление движения, но никогда не изменит скорость.

Математический расчет

Для движущихся объектов количество работы/времени (мощность) интегрируется вдоль траектории точки приложения силы. Таким образом, в любой момент времени скорость работы, совершаемой силой (измеряемая в джоулях/секунду или ваттах ), является скалярным произведением силы (вектора) и вектора скорости точки приложения. Это скалярное произведение силы и скорости известно как мгновенная мощность . Так же, как скорости могут быть интегрированы по времени для получения общего расстояния, по фундаментальной теореме исчисления , полная работа вдоль пути аналогично является интегралом по времени мгновенной мощности, приложенной вдоль траектории точки приложения. ^[19]

Работа — это результат силы, действующей на точку, которая следует по кривой X со скоростью v в каждый момент времени. Небольшое количество работы δW , которое происходит за момент времени dt, вычисляется как где F ⋅ v — это мощность за момент времени dt . Сумма этих небольших количеств работы по траектории точки дает работу, где C — это траектория от x ( t ₁ ) до x ( t ₂ ). Этот интеграл вычисляется вдоль траектории частицы и поэтому называется зависимым от пути . $${\displaystyle \delta W=\mathbf {F} \cdot d\mathbf {s} =\mathbf {F} \cdot \mathbf {v} dt}$$ $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} \,dt=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\tfrac {d\mathbf {s} }{dt}}\,dt=\int _{C}\mathbf {F} \cdot d\mathbf {s} ,}$$

Если сила всегда направлена ​​вдоль этой линии, а величина силы равна F , то этот интеграл упрощается до , где s — смещение вдоль линии. Если F постоянна, в дополнение к направлению вдоль линии, то интеграл упрощается еще больше до , где s — смещение точки вдоль линии. $${\displaystyle W=\int _{C}F\,ds}$$ $${\displaystyle W=\int _{C}F\,ds=F\int _{C}ds=Fs}$$

Этот расчет можно обобщить для постоянной силы, которая не направлена ​​вдоль линии, за которой следует частица. В этом случае скалярное произведение F ⋅ d s = F cos θ ds , где θ — угол между вектором силы и направлением движения, ^[19] то есть $${\displaystyle W=\int _{C}\mathbf {F} \cdot d\mathbf {s} =Fs\cos \theta .}$$

Когда компонент силы перпендикулярен смещению объекта (например, когда тело движется по круговой траектории под действием центральной силы ), работа не совершается, поскольку косинус 90° равен нулю. ^[14] Таким образом, гравитация не может совершить работу на планете с круговой орбитой (это идеальный вариант, поскольку все орбиты слегка эллиптические). Кроме того, работа не совершается на теле, движущемся по кругу с постоянной скоростью, будучи ограниченным механической силой, например, движущемся с постоянной скоростью в идеальной центрифуге без трения.

Работа, совершаемая переменной силой

Расчет работы как «сила, умноженная на отрезок прямого пути» применим только в самых простых обстоятельствах, как отмечено выше. Если сила изменяется или тело движется по криволинейной траектории, возможно, вращаясь и не обязательно будучи жестким, то для выполненной работы имеет значение только траектория точки приложения силы, и только компонент силы, параллельный скорости точки приложения, выполняет работу (положительная работа, когда в том же направлении, и отрицательная, когда в противоположном направлении скорости). Этот компонент силы можно описать скалярной величиной, называемой скалярным тангенциальным компонентом ( F cos( θ ) , где θ — угол между силой и скоростью). И тогда самое общее определение работы можно сформулировать следующим образом:

Площадь под кривой показывает работу, совершаемую F(x).

Работа, совершаемая переменной силой, представляет собой линейный интеграл ее скалярной тангенциальной составляющей вдоль траектории ее точки приложения.

Если сила меняется (например, сжимая пружину), нам нужно использовать исчисление, чтобы найти выполненную работу. Если сила как переменная x задана как F ( x ) , то работа, выполненная силой вдоль оси x от x ₁ до x _2, равна:

$${\displaystyle W=\lim _{\Delta \mathbf {x} \to 0}\sum _{x_{1}}^{x_{2}}\mathbf {F(x)} \Delta \mathbf {x} =\int _{x_{1}}^{x_{2}}\mathbf {F(x)} d\mathbf {x} .}$$

Таким образом, работа, совершаемая при переменной силе, может быть выражена как определенный интеграл силы по смещению. ^[20]

Если смещение как переменная времени задано как ∆ x (t) , то работа, совершаемая переменной силой от t ₁ до t _2, равна:

$${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} (t)\cdot \mathbf {v} (t)dt=\int _{t_{1}}^{t_{2}}P(t)dt.}$$

Таким образом, работа, совершаемая переменной силой, может быть выражена как определенный интеграл мощности по времени.

Крутящий момент и вращение

Пара сил возникает из равных и противоположных сил, действующих на две разные точки твердого тела. Сумма (результирующая) этих сил может сократиться, но их воздействие на тело — это пара или крутящий момент T . Работа крутящего момента вычисляется как , где T ⋅ ω — мощность над моментом dt . Сумма этих малых количеств работы по траектории твердого тела дает работу, Этот интеграл вычисляется вдоль траектории твердого тела с угловой скоростью ω, которая изменяется со временем, и поэтому называется зависящей от пути . $${\displaystyle \delta W=\mathbf {T} \cdot {\boldsymbol {\omega }}\,dt,}$$ $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\boldsymbol {\omega }}\,dt.}$$

Если вектор угловой скорости сохраняет постоянное направление, то он принимает вид, где — угол поворота вокруг постоянного единичного вектора S . В этом случае работа крутящего момента становится, где C — траектория от до . Этот интеграл зависит от траектории вращения и, следовательно, зависит от пути. $${\displaystyle {\boldsymbol {\omega }}={\dot {\phi }}\mathbf {S} ,}$$ ${\displaystyle \phi }$ $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot {\boldsymbol {\omega }}\,dt=\int _{t_{1}}^{t_{2}}\mathbf {T} \cdot \mathbf {S} {\frac {d\phi }{dt}}dt=\int _{C}\mathbf {T} \cdot \mathbf {S} \,d\phi ,}$$ ${\displaystyle \phi (t_{1})}$ ${\displaystyle \phi (t_{2})}$ ${\displaystyle \phi (t)}$

Если крутящий момент совмещен с вектором угловой скорости так, что T = τ S , {\displaystyle \mathbf {T} =\tau \mathbf {S} ,} и крутящий момент и угловая скорость постоянны, то работа принимает вид, ^[2] ${\displaystyle \tau }$ $${\displaystyle W=\int _{t_{1}}^{t_{2}}\tau {\dot {\phi }}\,dt=\tau (\phi _{2}-\phi _{1}).}$$

Сила постоянной величины, перпендикулярная плечу рычага

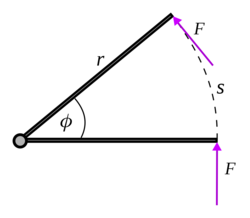
Этот результат можно понять проще, рассматривая крутящий момент как возникающий из силы постоянной величины F , приложенной перпендикулярно к плечу рычага на расстоянии , как показано на рисунке. Эта сила будет действовать на расстоянии вдоль дуги окружности , поэтому проделанная работа равна Введем крутящий момент τ = Fr , чтобы получить то, что представлено выше. ${\displaystyle r}$ ${\displaystyle l=s=r\phi }$ $${\displaystyle W=Fs=Fr\phi .}$$ $${\displaystyle W=Fr\phi =\tau \phi ,}$$

Обратите внимание, что в работу вносит вклад только та составляющая крутящего момента, которая направлена ​​в направлении вектора угловой скорости.

Работа и потенциальная энергия

Скалярное произведение силы F и скорости v точки ее приложения определяет мощность , подводимую к системе в момент времени. Интеграция этой мощности по траектории точки приложения, C = x ( t ) , определяет работу, подводимую к системе силой.

Зависимость от пути

Таким образом, работа, выполняемая силой F над объектом, движущимся по кривой C, задается линейным интегралом : где dx ( t ) определяет траекторию C , а v — скорость вдоль этой траектории. В общем случае этот интеграл требует, чтобы путь, вдоль которого определяется скорость, поэтому говорят, что оценка работы зависит от пути. $${\displaystyle W=\int _{C}\mathbf {F} \cdot d\mathbf {x} =\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt,}$$

Производная по времени от интеграла работы дает мгновенную мощность, $${\displaystyle {\frac {dW}{dt}}=P(t)=\mathbf {F} \cdot \mathbf {v} .}$$

Независимость пути

Если работа для приложенной силы не зависит от пути, то работа, выполненная силой, по теореме о градиенте , определяет потенциальную функцию, которая вычисляется в начале и конце траектории точки приложения. Это означает, что существует потенциальная функция U ( x ) , которая может быть вычислена в двух точках x ( t ₁ ) и x ( t ₂ ), чтобы получить работу по любой траектории между этими двумя точками. Традиционно эту функцию определяют с отрицательным знаком, так что положительная работа является уменьшением потенциала, то есть $${\displaystyle W=\int _{C}\mathbf {F} \cdot d\mathbf {x} =\int _{\mathbf {x} (t_{1})}^{\mathbf {x} (t_{2})}\mathbf {F} \cdot d\mathbf {x} =U(\mathbf {x} (t_{1}))-U(\mathbf {x} (t_{2})).}$$

Функция U ( x ) называется потенциальной энергией, связанной с приложенной силой. Сила, полученная из такой потенциальной функции, называется консервативной . Примерами сил, имеющих потенциальную энергию, являются сила тяжести и сила пружины.

В этом случае градиент работы дает ∇ W = − ∇ U = − ( ∂ U ∂ x , ∂ U ∂ y , ∂ U ∂ z ) = F , {\displaystyle \nabla W=-\nabla U=-\left({\frac {\partial U}{\partial x}},{\frac {\partial U}{\partial y}},{\frac {\partial U}{\partial z}}\right)=\mathbf {F} ,} и говорят, что сила F «выводится из потенциала». ^[21]

Поскольку потенциал U определяет силу F в каждой точке x в пространстве, набор сил называется силовым полем . Мощность, приложенная к телу силовым полем, получается из градиента работы, или потенциала, в направлении скорости V тела, то есть P ( t ) = − ∇ U ⋅ v = F ⋅ v . {\displaystyle P(t)=-\nabla U\cdot \mathbf {v} =\mathbf {F} \cdot \mathbf {v} .}

Работа под действием силы тяжести

Сила тяжести F = mg совершает работу W = mgh вдоль любого нисходящего пути

При отсутствии других сил гравитация приводит к постоянному ускорению вниз каждого свободно движущегося объекта. Вблизи поверхности Земли ускорение, вызванное силой тяжести, составляет g = 9,8 м⋅с ⁻² , а сила гравитации, действующая на объект массой m, составляет F _g = mg . Удобно представить, что эта сила гравитации сосредоточена в центре масс объекта.

Если объект весом mg перемещается вверх или вниз на вертикальное расстояние y ₂ − y ₁ , работа W, совершаемая над объектом, равна: где F _g — вес (фунты в имперских единицах и ньютоны в единицах СИ), а Δ y — изменение высоты y . Обратите внимание, что работа, совершаемая силой тяжести, зависит только от вертикального перемещения объекта. Наличие трения не влияет на работу, совершаемую над объектом его весом. $${\displaystyle W=F_{g}(y_{2}-y_{1})=F_{g}\Delta y=mg\Delta y}$$

В космосе

Сила тяжести, действующая со стороны массы M на другую массу m, определяется по формуле , где r — радиус-вектор от M к m , а r̂ — единичный вектор в направлении r . $${\displaystyle \mathbf {F} =-{\frac {GMm}{r^{2}}}{\hat {\mathbf {r} }}=-{\frac {GMm}{r^{3}}}\mathbf {r} ,}$$

Пусть масса m движется со скоростью v ; тогда работа силы тяжести над этой массой при ее движении из положения r ( t ₁ ) в положение r ( t ₂ ) определяется выражением Обратите внимание, что положение и скорость массы m определяются выражением где e _r и e _t — радиальный и тангенциальный единичные векторы, направленные относительно вектора от M к m , и мы используем тот факт, что Используйте это для упрощения формулы для работы силы тяжести до, Этот расчет использует тот факт, что Функция является функцией гравитационного потенциала, также известной как гравитационная потенциальная энергия . Отрицательный знак следует за соглашением, что работа приобретается за счет потери потенциальной энергии. $${\displaystyle W=-\int _{\mathbf {r} (t_{1})}^{\mathbf {r} (t_{2})}{\frac {GMm}{r^{3}}}\mathbf {r} \cdot d\mathbf {r} =-\int _{t_{1}}^{t_{2}}{\frac {GMm}{r^{3}}}\mathbf {r} \cdot \mathbf {v} \,dt.}$$ $${\displaystyle \mathbf {r} =r\mathbf {e} _{r},\qquad \mathbf {v} ={\frac {d\mathbf {r} }{dt}}={\dot {r}}\mathbf {e} _{r}+r{\dot {\theta }}\mathbf {e} _{t},}$$ ${\displaystyle d\mathbf {e} _{r}/dt={\dot {\theta }}\mathbf {e} _{t}.}$ $${\displaystyle W=-\int _{t_{1}}^{t_{2}}{\frac {GmM}{r^{3}}}(r\mathbf {e} _{r})\cdot \left({\dot {r}}\mathbf {e} _{r}+r{\dot {\theta }}\mathbf {e} _{t}\right)dt=-\int _{t_{1}}^{t_{2}}{\frac {GmM}{r^{3}}}r{\dot {r}}dt={\frac {GMm}{r(t_{2})}}-{\frac {GMm}{r(t_{1})}}.}$$ $${\displaystyle {\frac {d}{dt}}r^{-1}=-r^{-2}{\dot {r}}=-{\frac {\dot {r}}{r^{2}}}.}$$ $${\displaystyle U=-{\frac {GMm}{r}},}$$

Работа пружиной

Силы в пружинах, собранных параллельно

Рассмотрим пружину, которая оказывает горизонтальную силу F = (− kx , 0, 0) , которая пропорциональна ее отклонению в направлении x независимо от того, как движется тело. Работа этой пружины над телом, движущимся по пространству с кривой X ( t ) = ( x ( t ), y ( t ), z ( t )) , вычисляется с использованием ее скорости, v = ( v _x , v _y , v _z ) , чтобы получить Для удобства рассмотрим контакт с пружиной, происходящий при t = 0 , тогда интеграл произведения расстояния x и x-скорости, xv _x dt , по времени t равен ⁠ $${\displaystyle W=\int _{0}^{t}\mathbf {F} \cdot \mathbf {v} dt=-\int _{0}^{t}kxv_{x}dt=-{\frac {1}{2}}kx^{2}.}$$1/2⁠ x ^2. Работа равна произведению расстояния на силу пружины, которая также зависит от расстояния; отсюда и результат x ² .

Работа газом

Работа, совершаемая телом газа над окружающей средой, равна: где P — давление, V — объем, а a и b — начальный и конечный объемы. ${\displaystyle W}$ $${\displaystyle W=\int _{a}^{b}P\,dV}$$

Принцип работы–энергии

Принцип работы и кинетической энергии (также известный как принцип работы–энергии ) гласит, что работа, совершаемая всеми силами, действующими на частицу (работа результирующей силы), равна изменению кинетической энергии частицы. ^[22] То есть работа W, совершаемая результирующей силой, действующей на частицу, равна изменению кинетической энергии частицы , ^[2] где и — скорости частицы до и после совершения работы, а m — ее масса . ${\displaystyle E_{\text{k}}}$ $${\displaystyle W=\Delta E_{\text{k}}={\frac {1}{2}}mv_{2}^{2}-{\frac {1}{2}}mv_{1}^{2}}$$ ${\displaystyle v_{1}}$ ${\displaystyle v_{2}}$

Вывод принципа работы-энергии начинается со второго закона движения Ньютона и результирующей силы, действующей на частицу. Вычисление скалярного произведения силы на скорость частицы оценивает мгновенную мощность, добавленную к системе. ^[23] (Ограничения определяют направление движения частицы, гарантируя, что нет компонента скорости в направлении силы ограничения. Это также означает, что силы ограничения не добавляются к мгновенной мощности.) Интеграл по времени этого скалярного уравнения дает работу из мгновенной мощности и кинетическую энергию из скалярного произведения ускорения на скорость. Тот факт, что принцип работы-энергии устраняет силы ограничения, лежит в основе механики Лагранжа . ^[24]

В этом разделе основное внимание уделяется принципу работы–энергии в его применении к динамике частиц. В более общих системах работа может изменять потенциальную энергию механического устройства, тепловую энергию в тепловой системе или электрическую энергию в электрическом устройстве. Работа переносит энергию из одного места в другое или из одной формы в другую.

Вывод для частицы, движущейся по прямой линии

В случае, если результирующая сила F постоянна как по величине, так и по направлению и параллельна скорости частицы, частица движется с постоянным ускорением a вдоль прямой линии. ^[25] Связь между результирующей силой и ускорением задается уравнением F = ma ( второй закон Ньютона ), а смещение частицы s можно выразить уравнением , которое следует из (см. Уравнения движения ). $${\displaystyle s={\frac {v_{2}^{2}-v_{1}^{2}}{2a}}}$$ ${\displaystyle v_{2}^{2}=v_{1}^{2}+2as}$

Работа чистой силы вычисляется как произведение ее величины на смещение частицы. Подставляя приведенные выше уравнения, получаем: $${\displaystyle W=Fs=mas=ma{\frac {v_{2}^{2}-v_{1}^{2}}{2a}}={\frac {1}{2}}mv_{2}^{2}-{\frac {1}{2}}mv_{1}^{2}=\Delta E_{\text{k}}}$$

Другое происхождение: $${\displaystyle W=Fs=mas=m{\frac {v_{2}^{2}-v_{1}^{2}}{2s}}s={\frac {1}{2}}mv_{2}^{2}-{\frac {1}{2}}mv_{1}^{2}=\Delta E_{\text{k}}}$$

В общем случае прямолинейного движения, когда результирующая сила F не постоянна по величине, но постоянна по направлению и параллельна скорости частицы, работа должна быть проинтегрирована вдоль траектории частицы: $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=\int _{t_{1}}^{t_{2}}F\,v\,dt=\int _{t_{1}}^{t_{2}}ma\,v\,dt=m\int _{t_{1}}^{t_{2}}v\,{\frac {dv}{dt}}\,dt=m\int _{v_{1}}^{v_{2}}v\,dv={\tfrac {1}{2}}m\left(v_{2}^{2}-v_{1}^{2}\right).}$$

Общий вывод принципа работы-энергии для частицы

Для любой чистой силы, действующей на частицу, движущуюся по любой криволинейной траектории, можно продемонстрировать, что ее работа равна изменению кинетической энергии частицы с помощью простого вывода, аналогичного уравнению выше. Это известно как принцип работы-энергии : $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot \mathbf {v} dt=m\int _{t_{1}}^{t_{2}}\mathbf {a} \cdot \mathbf {v} dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {dv^{2}}{dt}}\,dt={\frac {m}{2}}\int _{v_{1}^{2}}^{v_{2}^{2}}dv^{2}={\frac {mv_{2}^{2}}{2}}-{\frac {mv_{1}^{2}}{2}}=\Delta E_{\text{k}}}$$

Тождество требует некоторой алгебры. Из тождества и определения следует ${\textstyle \mathbf {a} \cdot \mathbf {v} ={\frac {1}{2}}{\frac {dv^{2}}{dt}}}$ ${\textstyle v^{2}=\mathbf {v} \cdot \mathbf {v} }$ ${\textstyle \mathbf {a} ={\frac {d\mathbf {v} }{dt}}}$ $${\displaystyle {\frac {dv^{2}}{dt}}={\frac {d(\mathbf {v} \cdot \mathbf {v} )}{dt}}={\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} +\mathbf {v} \cdot {\frac {d\mathbf {v} }{dt}}=2{\frac {d\mathbf {v} }{dt}}\cdot \mathbf {v} =2\mathbf {a} \cdot \mathbf {v} .}$$

Оставшаяся часть приведенного выше вывода представляет собой простое исчисление, такое же, как и в предыдущем прямолинейном случае.

Вывод для частицы в ограниченном движении

В динамике частиц формула, приравнивающая работу, приложенную к системе, к изменению ее кинетической энергии, получается как первый интеграл второго закона движения Ньютона . Полезно отметить, что результирующая сила, используемая в законах Ньютона, может быть разделена на силы, приложенные к частице, и силы, налагаемые ограничениями на движение частицы. Примечательно, что работа силы ограничения равна нулю, поэтому в принципе работы–энергии необходимо учитывать только работу приложенных сил.

Чтобы увидеть это, рассмотрим частицу P, которая следует по траектории X ( t ) с действующей на нее силой F. Изолируем частицу от ее окружения, чтобы выявить силы ограничения R , тогда закон Ньютона примет вид, где m — масса частицы. $${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }},}$$

Векторная формулировка

Обратите внимание, что n точек над вектором указывают на его n-ную производную по времени . Скалярное произведение каждой стороны закона Ньютона с вектором скорости дает, поскольку силы ограничения перпендикулярны скорости частицы. Интегрируем это уравнение вдоль его траектории от точки X ( t ₁ ) до точки X ( t ₂ ), чтобы получить $${\displaystyle \mathbf {F} \cdot {\dot {\mathbf {X} }}=m{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }},}$$ $${\displaystyle \int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\dot {\mathbf {X} }}dt=m\int _{t_{1}}^{t_{2}}{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}dt.}$$

Левая часть этого уравнения представляет собой работу приложенной силы, действующей на частицу вдоль траектории от времени t ₁ до времени t _2. Это также можно записать как Этот интеграл вычисляется вдоль траектории X ( t ) частицы и, следовательно, зависит от пути. $${\displaystyle W=\int _{t_{1}}^{t_{2}}\mathbf {F} \cdot {\dot {\mathbf {X} }}dt=\int _{\mathbf {X} (t_{1})}^{\mathbf {X} (t_{2})}\mathbf {F} \cdot d\mathbf {X} .}$$

Правую часть первого интеграла уравнений Ньютона можно упростить, используя следующее тождество (см. правило произведения для вывода). Теперь оно интегрируется явно, чтобы получить изменение кинетической энергии, где кинетическая энергия частицы определяется скалярной величиной, $${\displaystyle {\frac {1}{2}}{\frac {d}{dt}}({\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }})={\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }},}$$ $${\displaystyle \Delta K=m\int _{t_{1}}^{t_{2}}{\ddot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {d}{dt}}({\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }})dt={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}(t_{2})-{\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}(t_{1})={\frac {1}{2}}m\Delta \mathbf {v} ^{2},}$$ $${\displaystyle K={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}={\frac {1}{2}}m{\mathbf {v} ^{2}}}$$

Тангенциальные и нормальные компоненты

Полезно разложить векторы скорости и ускорения на тангенциальную и нормальную составляющие вдоль траектории X ( t ) , так что где Тогда скалярное произведение скорости на ускорение во втором законе Ньютона принимает вид где кинетическая энергия частицы определяется скалярной величиной, $${\displaystyle {\dot {\mathbf {X} }}=v\mathbf {T} \quad {\text{and}}\quad {\ddot {\mathbf {X} }}={\dot {v}}\mathbf {T} +v^{2}\kappa \mathbf {N} ,}$$ $${\displaystyle v=|{\dot {\mathbf {X} }}|={\sqrt {{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}}}.}$$ $${\displaystyle \Delta K=m\int _{t_{1}}^{t_{2}}{\dot {v}}v\,dt={\frac {m}{2}}\int _{t_{1}}^{t_{2}}{\frac {d}{dt}}v^{2}\,dt={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}),}$$ $${\displaystyle K={\frac {m}{2}}v^{2}={\frac {m}{2}}{\dot {\mathbf {X} }}\cdot {\dot {\mathbf {X} }}.}$$

Результатом является принцип работы и энергии для динамики частиц. Этот вывод можно обобщить на произвольные системы твердых тел. $${\displaystyle W=\Delta K.}$$

Движение по прямой (торможение до полной остановки)

Рассмотрим случай транспортного средства, движущегося по прямой горизонтальной траектории под действием движущей силы и силы тяжести, которые в сумме дают F. Силы связи между транспортным средством и дорогой определяют R , и мы имеем Для удобства пусть траектория будет вдоль оси X, так что X = ( d , 0) , а скорость равна V = ( v , 0) , тогда R ⋅ V = 0 , и F ⋅ V = F _x v , где F _x — составляющая F вдоль оси X, так что Интегрирование обеих частей дает Если F _x постоянна вдоль траектории, то интеграл скорости равен расстоянию, так что $${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }}.}$$ $${\displaystyle F_{x}v=m{\dot {v}}v.}$$ $${\displaystyle \int _{t_{1}}^{t_{2}}F_{x}vdt={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}).}$$ $${\displaystyle F_{x}(d(t_{2})-d(t_{1}))={\frac {m}{2}}v^{2}(t_{2})-{\frac {m}{2}}v^{2}(t_{1}).}$$

В качестве примера рассмотрим автомобиль, занос которого приводит к остановке, где k — коэффициент трения, а W — вес автомобиля. Тогда сила вдоль траектории равна F _x = − kW . Скорость v автомобиля можно определить по длине s заноса, используя принцип работы и энергии. Эта формула использует тот факт, что масса автомобиля равна m = W / g . $${\displaystyle kWs={\frac {W}{2g}}v^{2},\quad {\text{or}}\quad v={\sqrt {2ksg}}.}$$

Гоночный автомобиль Lotus Type 119B Gravity на праздновании 60-летия Lotus

Чемпионат по гравитационным гонкам в Кампус-Новус, Санта-Катарина, Бразилия, 8 сентября 2010 г.

Движение по наклонной поверхности (гравитационные гонки)

Рассмотрим случай транспортного средства, которое начинает движение из состояния покоя и движется по наклонной поверхности (например, по горной дороге), принцип работы-энергии помогает вычислить минимальное расстояние, которое проходит транспортное средство, чтобы достичь скорости V , скажем, 60 миль в час (88 футов в секунду). Сопротивление качению и сопротивление воздуха замедлят транспортное средство, поэтому фактическое расстояние будет больше, чем если бы этими силами пренебречь.

Пусть траектория движения транспортного средства по дороге будет X ( t ), что является кривой в трехмерном пространстве. Сила, действующая на транспортное средство, которая толкает его по дороге, является постоянной силой тяжести F = (0, 0, W ) , в то время как сила дороги на транспортное средство является силой ограничения R . Второй закон Ньютона дает, Скалярное произведение этого уравнения на скорость, V = ( v _x , v _y , v _z ) , дает где V - величина V . Силы ограничения между транспортным средством и дорогой сокращаются из этого уравнения, поскольку R ⋅ V = 0 , что означает, что они не выполняют работу. Интегрируем обе части, чтобы получить Сила веса W постоянна вдоль траектории, а интеграл вертикальной скорости - это вертикальное расстояние, поэтому, Напомним, что V( t ₁ )=0. Обратите внимание, что этот результат не зависит от формы дороги, по которой движется транспортное средство. $${\displaystyle \mathbf {F} +\mathbf {R} =m{\ddot {\mathbf {X} }}.}$$ $${\displaystyle Wv_{z}=m{\dot {V}}V,}$$ $${\displaystyle \int _{t_{1}}^{t_{2}}Wv_{z}dt={\frac {m}{2}}V^{2}(t_{2})-{\frac {m}{2}}V^{2}(t_{1}).}$$ $${\displaystyle W\Delta z={\frac {m}{2}}V^{2}.}$$

Чтобы определить расстояние по дороге, предположим, что уклон составляет 6%, что является крутой дорогой. Это означает, что высота уменьшается на 6 футов на каждые пройденные 100 футов — для таких малых углов функции sin и tan приблизительно равны. Таким образом, расстояние s в футах вниз по уклону 6%, необходимое для достижения скорости V, составляет не менее Эта формула использует тот факт, что вес транспортного средства равен W = mg . $${\displaystyle s={\frac {\Delta z}{0.06}}=8.3{\frac {V^{2}}{g}},\quad {\text{or}}\quad s=8.3{\frac {88^{2}}{32.2}}\approx 2000\mathrm {ft} .}$$

Работа сил, действующих на твердое тело

Работу сил, действующих в различных точках на одно твердое тело, можно вычислить из работы результирующей силы и крутящего момента . Чтобы увидеть это, пусть силы F ₁ , F ₂ , ..., F _n действуют на точки X ₁ , X ₂ , ..., X _n в твердом теле.

Траектории X _i , i = 1, ..., n определяются движением твердого тела. Это движение задается набором вращений [ A ( t )] и траекторией d ( t ) опорной точки в теле. Пусть координаты x _i i = 1, ..., n определяют эти точки в системе отсчета движущегося твердого тела M , так что траектории, прослеживаемые в неподвижной системе F , задаются как $${\displaystyle \mathbf {X} _{i}(t)=[A(t)]\mathbf {x} _{i}+\mathbf {d} (t)\quad i=1,\ldots ,n.}$$

Скорость точек X _i вдоль их траекторий равна где ω — вектор угловой скорости, полученный из кососимметричной матрицы, известной как матрица угловой скорости. $${\displaystyle \mathbf {V} _{i}={\boldsymbol {\omega }}\times (\mathbf {X} _{i}-\mathbf {d} )+{\dot {\mathbf {d} }},}$$ $${\displaystyle [\Omega ]={\dot {A}}A^{\mathsf {T}},}$$

Небольшую величину работы сил над малыми смещениями δ r _i можно определить, аппроксимируя смещение выражением δ r = v δt так или $${\displaystyle \delta W=\mathbf {F} _{1}\cdot \mathbf {V} _{1}\delta t+\mathbf {F} _{2}\cdot \mathbf {V} _{2}\delta t+\ldots +\mathbf {F} _{n}\cdot \mathbf {V} _{n}\delta t}$$ $${\displaystyle \delta W=\sum _{i=1}^{n}\mathbf {F} _{i}\cdot ({\boldsymbol {\omega }}\times (\mathbf {X} _{i}-\mathbf {d} )+{\dot {\mathbf {d} }})\delta t.}$$

Эту формулу можно переписать так, чтобы получить где F и T — результирующая сила и крутящий момент, приложенные в опорной точке d подвижной системы координат M в твердом теле. $${\displaystyle \delta W=\left(\sum _{i=1}^{n}\mathbf {F} _{i}\right)\cdot {\dot {\mathbf {d} }}\delta t+\left(\sum _{i=1}^{n}\left(\mathbf {X} _{i}-\mathbf {d} \right)\times \mathbf {F} _{i}\right)\cdot {\boldsymbol {\omega }}\delta t=\left(\mathbf {F} \cdot {\dot {\mathbf {d} }}+\mathbf {T} \cdot {\boldsymbol {\omega }}\right)\delta t,}$$

Ссылки

1. NCERT (2020). "Physics Book" (PDF) . ncert.nic.in . Получено 24 ноября 2021 г. .
2. Хью Д. Янг и Роджер А. Фридман (2008). Университетская физика (12-е изд.). Эддисон-Уэсли. стр. 329. ISBN 978-0-321-50130-1.
3. Кребс, Роберт Э. (2004). Новаторские эксперименты, изобретения и открытия Средневековья. Greenwood Publishing Group. стр. 163. ISBN 978-0-313-32433-8. Получено 21.05.2008 .
4. Стивен, Дональд; Лоуэлл Кардвелл (2001). Колеса, часы и ракеты: история технологий. США: WW Norton & Company. стр. 85–87. ISBN 978-0-393-32175-3.
5. Мендельсон, Кеннет С. (2003-02-13). «Физические и разговорные значения термина «работа»». American Journal of Physics . 71 (3): 279–281. doi :10.1119/1.1522707. ISSN  0002-9505.
6. Декарт, Р. (2013) [Письмо Гюйгенсу, 5 октября 1637 г.]. Беннетт, Дж. (ред.). Избранная переписка Декарта (PDF) . стр. 50.
7. Илтис, К. (1971). «Лейбниц и полемика о живой силе» (PDF) . Isis . 62 (1): 21–35 (в частности, стр. 24). doi :10.1086/350705. S2CID  143652761.
8. Смитон, Джон (1759). «Экспериментальное исследование естественных сил воды и ветра, приводящих мельницы и другие машины в движение с помощью кругового движения». Philosophical Transactions of the Royal Society . 51 : 105. doi : 10.1098/rstl.1759.0019 . S2CID  186213498.
9. Джеммер, Макс (1957). Концепции силы. Dover Publications, Inc. стр. 167; сноска 14. ISBN 0-486-40689-X.
10. Кориолис, Гюстав (1829). Расчет действия машин, или соображения об использовании двигателей и их оценке. Carilian-Goeury, Libraire (Париж).
11. Дюгас, Р. (1955). История механики. Швейцария: Éditions du Griffon. стр. 128.
12. "Единицы со специальными названиями и символами; единицы, которые включают специальные названия и символы". Международная система единиц (СИ) (8-е изд.). Международное бюро мер и весов . 2006. Архивировано из оригинала 20-04-2013 . Получено 27-10-2012 .
13. McGrath, Kimberley A., ред. (5 мая 2010 г.). Мир физики (1-е изд.). Детройт: Gale. Работа и потенциальная энергия. ISBN 978-0-7876-3651-7.
14. Walker, Jearl; Halliday, David; Resnick, Robert (2011). Основы физики (9-е изд.). Hoboken, NJ: Wiley. стр. 154. ISBN 9780470469118.
15. Голдштейн, Герберт (2002). Классическая механика (3-е изд.). Сан-Франциско: Addison Wesley. ISBN 978-0-201-65702-9. OCLC  47056311.
16. Рогальский, Мирча С. (2018). Advanced University Physics (2-е изд.). Бока-Ратон: Chapman and Hall/CRC. ISBN 9781351991988.
17. "Фейнмановские лекции по физике, том I, гл. 14: Работа и потенциальная энергия (заключение)". feynmanlectures.caltech.edu .
18. Гринвуд, Дональд Т. (1997). Классическая динамика . Минеола, Нью-Йорк: Dover Publications. ISBN 9780486138794.
19. Resnick, Robert, Halliday, David (1966), Physics , Section 1–3 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
20. "MindTap - Cengage Learning". ng.cengage.com . Получено 2023-10-16 .
21. Тейлор, Джон Р. (2005). Классическая механика. Университетские научные книги. ISBN 978-1-891389-22-1.
22. Эндрю Питель; Яан Киусалаас (2010). Инженерная механика: Динамика – Версия SI, Том 2 (3-е изд.). Cengage Learning. стр. 654. ISBN 9780495295631.
23. Пол, Бертон (1979). Кинематика и динамика плоских машин. Prentice-Hall. ISBN 978-0-13-516062-6.
24. Уиттекер, ET (1904). Трактат об аналитической динамике частиц и твердых тел. Cambridge University Press.
25. "Работа–энергия принцип". www.wwu.edu . Архивировано из оригинала 2012-05-30 . Получено 2012-08-06 .

Библиография

• Serway, Raymond A.; Jewett, John W. (2004). Физика для ученых и инженеров (6-е изд.). Brooks/Cole. ISBN 0-534-40842-7.
• Типлер, Пол (1991). Физика для ученых и инженеров: Механика (3-е изд., расширенная версия ред.). WH Freeman. ISBN 0-87901-432-6.

Внешние ссылки

• Принцип работы–энергии