множество Кантора

Множество точек на отрезке прямой

В математике множество Кантора — это множество точек, лежащих на одном отрезке прямой , обладающее рядом неинтуитивных свойств. Оно было открыто в 1874 году Генри Джоном Стивеном Смитом ^{[1] [2] [3] [4]} и упомянуто немецким математиком Георгом Кантором в 1883 году. ^{[5] [6]}

Рассматривая это множество, Кантор и другие помогли заложить основы современной топологии точечных множеств . Наиболее распространенной конструкцией является троичное множество Кантора , построенное путем удаления средней трети отрезка прямой, а затем повторения процесса с оставшимися более короткими отрезками. Кантор упомянул эту троичную конструкцию лишь мимоходом, как пример совершенного множества , которое нигде не плотно (, ^[5] Anmerkungen zu §10, /стр. 590).

В более общем смысле, в топологии, пространство Кантора — это топологическое пространство, гомеоморфное тернарному множеству Кантора (оснащенное его топологией подпространства). По теореме LEJ Brouwer это эквивалентно тому, что оно совершенно, непусто, компактно, метризуемо и имеет нулевую размерность. ^[7]

Расширение множества Кантора. Каждая точка множества представлена ​​здесь вертикальной линией.

Построение и формула троичного множества

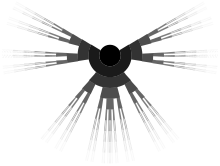
Тройной набор Кантора создается путем итеративного удаления открытой средней трети из набора отрезков. Начинается с удаления открытой средней трети из интервала , оставляя два отрезка: . Затем удаляется открытая средняя треть каждого из этих оставшихся отрезков, оставляя четыре отрезка: . Тройной набор Кантора содержит все точки в интервале , которые не удаляются ни на одном шаге этого бесконечного процесса . Те же факты можно описать рекурсивно, установив ${\displaystyle {\mathcal {C}}}$ ${\textstyle \left({\frac {1}{3}},{\frac {2}{3}}\right)}$ ${\displaystyle \textstyle \left[0,1\right]}$ ${\textstyle \left[0,{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},1\right]}$ ${\textstyle \left[0,{\frac {1}{9}}\right]\cup \left[{\frac {2}{9}},{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},{\frac {7}{9}}\right]\cup \left[{\frac {8}{9}},1\right]}$ ${\displaystyle [0,1]}$

${\displaystyle C_{0}:=[0,1]}$

и

${\displaystyle C_{n}:={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}}{3}}\right)={\frac {1}{3}}{\bigl (}C_{n-1}\cup \left(2+C_{n-1}\right){\bigr )}}$

для , так что ${\displaystyle n\geq 1}$

${\displaystyle {\mathcal {C}}:=}$ ${\displaystyle {\color {Blue}\lim _{n\to \infty }C_{n}}}$ ${\displaystyle =\bigcap _{n=0}^{\infty }C_{n}=\bigcap _{n=m}^{\infty }C_{n}}$   для любого   . ${\displaystyle m\geq 0}$

Первые шесть шагов этого процесса проиллюстрированы ниже.

Используя идею самоподобных преобразований, и явные замкнутые формулы для множества Кантора ^[8] ${\displaystyle T_{L}(x)=x/3,}$ ${\displaystyle T_{R}(x)=(2+x)/3}$ ${\displaystyle C_{n}=T_{L}(C_{n-1})\cup T_{R}(C_{n-1}),}$

${\displaystyle {\mathcal {C}}=[0,1]\,\setminus \,\bigcup _{n=0}^{\infty }\bigcup _{k=0}^{3^{n}-1}\left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)\!,}$

где каждая средняя треть удаляется как открытый интервал из окружающего его закрытого интервала , или ${\textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$ ${\textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[{\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\right]}$

${\displaystyle {\mathcal {C}}=\bigcap _{n=1}^{\infty }\bigcup _{k=0}^{3^{n-1}-1}\left(\left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\right)\!,}$

где средняя треть предыдущего замкнутого интервала удаляется путем пересечения с ${\textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$ ${\textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[{\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]}$ ${\textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\!.}$

Этот процесс удаления средних третей является простым примером правила конечного подразделения . Дополнение троичного множества Кантора является примером фрактальной строки .

В арифметических терминах множество Кантора состоит из всех действительных чисел единичного интервала , которым не требуется цифра 1 для выражения в виде троичной (основание 3) дроби. Как показано на приведенной выше диаграмме, каждая точка множества Кантора уникально расположена путем через бесконечно глубокое двоичное дерево , где путь поворачивает влево или вправо на каждом уровне в соответствии с тем, на какой стороне удаленного сегмента лежит точка. Представление каждого поворота влево с помощью 0 и каждого поворота вправо с помощью 2 дает троичную дробь для точки. ${\displaystyle [0,1]}$

Конструкция Мандельброта методом «свертывания»

В своей книге «Фрактальная геометрия природы » математик Бенуа Мандельброт предлагает причудливый мысленный эксперимент, чтобы помочь читателям, не разбирающимся в математике, представить себе конструкцию . Его повествование начинается с представления бруска, возможно, из легкого металла, в котором вещество бруска «свертывается», итеративно смещаясь к его концам. По мере того, как сегменты бруска становятся меньше, они превращаются в тонкие, плотные слизни, которые в конечном итоге становятся слишком маленькими и слабыми, чтобы их можно было увидеть. ${\displaystyle {\mathcal {C}}}$

СВЕРТЫВАНИЕ: Конструкция канторовой полосы является результатом процесса, который я называю свертыванием. Он начинается с круглой полосы. Лучше всего думать о ней как о имеющей очень низкую плотность. Затем материя «свертывается» из средней трети этой полосы в конечные трети, так что положение последних остается неизменным. Затем материя свертывается из средней трети каждой конечной трети в ее конечные трети, и так до бесконечности, пока не останется бесконечно большое количество бесконечно тонких слитков бесконечно высокой плотности. Эти слитки расположены вдоль линии очень специфическим образом, вызванным процессом генерации. На этой иллюстрации свертывание (которое в конечном итоге требует отбивания молотком!) прекращается, когда и пресс печатника, и наш глаз перестают следить; последняя строка неотличима от предпоследней: каждая из ее конечных частей видна как серый слиток, а не как два параллельных черных слитка. ^[9]

Состав

Поскольку множество Кантора определяется как множество неисключенных точек, то доля (т.е. мера ) оставшегося единичного интервала может быть найдена по общей удаленной длине. Эта общая сумма является геометрической прогрессией

${\displaystyle \sum _{n=0}^{\infty }{\frac {2^{n}}{3^{n+1}}}={\frac {1}{3}}+{\frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\left({\frac {1}{1-{\frac {2}{3}}}}\right)=1.}$

Так что оставшаяся пропорция равна 1 − 1 = 0.

Этот расчет предполагает, что множество Кантора не может содержать интервалов ненулевой длины. Может показаться удивительным, что что-то должно остаться — в конце концов, сумма длин удаленных интервалов равна длине исходного интервала. Однако более пристальный взгляд на процесс показывает, что что-то должно остаться, поскольку удаление «средней трети» каждого интервала включало удаление открытых множеств (множеств, которые не включают свои конечные точки). Таким образом, удаление отрезка прямой ( ⁠1/3⁠ , ⁠2/3⁠ ) ​​из исходного интервала [0, 1] оставляет позади точки ⁠1/3⁠ и ⁠2/3⁠ . Последующие шаги не удаляют эти (или другие) конечные точки, поскольку удаляемые интервалы всегда являются внутренними по отношению к оставшимся интервалам. Таким образом, множество Кантора не пусто и фактически содержит несчетное бесконечное число точек (как следует из приведенного выше описания в терминах путей в бесконечном двоичном дереве).

Может показаться, что остались только конечные точки сегментов конструкции, но это тоже не так. Число ⁠1/4⁠ , например, имеет уникальную троичную форму 0,020202... = 0, 02 . Он находится в нижней трети, и верхней трети этой трети, и нижней трети этой верхней трети, и так далее. Поскольку он никогда не находится ни в одном из средних сегментов, он никогда не удаляется. Тем не менее, он также не является конечной точкой любого среднего сегмента, потому что он не кратен никакой степени 1/3. ^[10] Все конечные точки сегментов являются конечными троичными дробями и содержатся в наборе

${\displaystyle \left\{x\in [0,1]\mid \exists i\in \mathbb {N} _{0}:x\,3^{i}\in \mathbb {Z} \right\}\qquad {\Bigl (}\subset \mathbb {N} _{0}\,3^{-\mathbb {N} _{0}}{\Bigr )}}$

что является счетно бесконечным множеством. Что касается мощности , то почти все элементы множества Кантора не являются ни конечными точками интервалов, ни рациональными точками вроде 1/4. Все множество Кантора на самом деле не счетно.

Характеристики

Мощность

Можно показать, что в этом процессе осталось столько же точек, сколько и было в начале, и поэтому множество Кантора несчетно . Чтобы увидеть это, покажем, что существует функция f из множества Кантора в замкнутый интервал [0,1], которая является сюръективной (т.е. f отображает из на [0,1]), так что мощность не меньше мощности [0,1]. Поскольку является подмножеством [0,1], ее мощность также не больше, поэтому две мощности должны быть фактически равны по теореме Кантора–Бернштейна–Шредера . ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$

Чтобы построить эту функцию, рассмотрим точки в интервале [0, 1] в терминах нотации с основанием 3 (или троичной ). Напомним, что правильные троичные дроби, точнее: элементы , допускают более одного представления в этой нотации, как, например , ⁠ ${\displaystyle {\bigl (}\mathbb {Z} \setminus \{0\}{\bigr )}\cdot 3^{-\mathbb {N} _{0}}}$1/3⁠ , что можно записать как 0,1 ₃ = 0,1 0 ₃ , но также как 0,0222... ₃ = 0,0 2 ₃ , и ⁠2/3⁠ , что можно записать как 0,2 ₃ = 0,2 0 ₃ , но также как 0,1222... ₃ = 0,1 2 ₃ . ^[11] Когда мы удаляем среднюю треть, она содержит числа с троичными числами вида 0,1xxxxx... ₃ , где xxxxx... ₃ строго между 00000... ₃ и 22222... ₃ . Таким образом, числа, оставшиеся после первого шага, состоят из

• Числа вида 0,0xxxxx... ₃ (включая 0,022222... ₃ = 1/3)
• Числа вида 0,2xxxxx... ₃ (включая 0,222222... ₃ = 1)

Это можно обобщить, сказав, что числа с троичным представлением, в которых первая цифра после запятой не равна 1, — это те числа, которые остаются после первого шага.

На втором этапе удаляются числа вида 0,01xxxx... ₃ и 0,21xxxx... ₃ , и (при соответствующем внимании к конечным точкам) можно сделать вывод, что оставшиеся числа — это числа с троичной системой счисления, где ни одна из первых двух цифр не равна 1.

Продолжая таким образом, для того, чтобы число не было исключено на шаге n , оно должно иметь троичное представление, n- я цифра которого не равна 1. Для того, чтобы число было в множестве Кантора, оно не должно быть исключено на любом шаге, оно должно допускать числовое представление, состоящее полностью из нулей и двоек.

Стоит подчеркнуть, что такие числа, как 1, ⁠1/3⁠ = 0,1 ₃ и ⁠7/9⁠ = 0,21 ₃ находятся в множестве Кантора, так как они имеют троичные числа, состоящие исключительно из нулей и двоек: 1 = 0,222... ₃ = 0. 2 ₃ , ⁠1/3⁠ = 0,0222... ₃ = 0,0 2 ₃ и ⁠7/9⁠ = 0,20222... ₃ = 0,20 2 ₃ . Все последние числа являются «конечными точками», а эти примеры являются правыми предельными точками . То же самое верно для левых предельных точек , например ⁠ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$2/3⁠ = 0,1222... ₃ = 0,1 2 ₃ = 0,2 0 ₃ и ⁠8/9⁠ = 0,21222... ₃ = 0,21 2 ₃ = 0,22 0 ₃ . Все эти конечные точки являются правильными троичными дробями (элементами ) вида ⁠ ${\displaystyle \mathbb {Z} \cdot 3^{-\mathbb {N} _{0}}}$п/д⁠ , где знаменатель q является степенью 3 , когда дробь находится в несократимой форме. ^[10] Троичное представление этих дробей заканчивается (т. е. конечно) или — напомним выше, что каждая правильная троичная дробь имеет 2 представления — бесконечно и «заканчивается» либо бесконечным числом повторяющихся нулей, либо бесконечным числом повторяющихся двоек. Такая дробь является левой предельной точкой , если ее троичное представление не содержит единиц и «заканчивается» бесконечным числом повторяющихся нулей. Аналогично правильная троичная дробь является правой предельной точкой , если ее троичное разложение не содержит единиц и «заканчивается» бесконечным числом повторяющихся двоек. ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$

Это множество конечных точек плотно в (но не плотно в [0, 1]) и составляет счетно бесконечное множество. Числа, в которых не являются конечными точками, также имеют только 0 и 2 в своем троичном представлении, но они не могут заканчиваться бесконечным повторением цифры 0 или цифры 2, потому что тогда это была бы конечная точка. ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$

Функция от до [0,1] определяется путем взятия троичных чисел, которые состоят полностью из нулей и двоек, замены всех двоек на единицы и интерпретации последовательности как двоичного представления действительного числа. В формуле, ${\displaystyle {\mathcal {C}}}$

${\displaystyle f{\bigg (}\sum _{k\in \mathbb {N} }a_{k}3^{-k}{\bigg )}=\sum _{k\in \mathbb {N} }{\frac {a_{k}}{2}}2^{-k}}$   где   ${\displaystyle \forall k\in \mathbb {N} :a_{k}\in \{0,2\}.}$

Для любого числа y в [0,1] его двоичное представление можно перевести в троичное представление числа x в заменой всех единиц на двойки. При этом f ( x ) = y , так что y находится в диапазоне f . Например, если y = ⁠ ${\displaystyle {\mathcal {C}}}$3/5⁠ = 0,100110011001... ₂ = 0,1001 , записываем x = 0,200220022002 ... ₃ = ⁠7/10⁠ . Следовательно, f сюръективен. Однако f не инъективен — значения, для которых f ( x ) совпадает , находятся на противоположных концах одной из удаленных средних третей . Например, возьмем

⁠1/3⁠ = 0,0 2 ₃ (что является правой предельной точкой и левой предельной точкой средней трети [ ⁠ ${\displaystyle {\mathcal {C}}}$1/3⁠ , ⁠2/3⁠ ]) и

⁠2/3⁠ = 0,2 0 ₃ (что является левой предельной точкой и правой предельной точкой средней трети [ ⁠ ${\displaystyle {\mathcal {C}}}$1/3⁠ , ⁠2/3⁠ ])

так

${\displaystyle {\begin{array}{lcl}f{\bigl (}{}^{1}\!\!/\!_{3}{\bigr )}=f(0.0{\overline {2}}_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0}}_{2}=f(0.2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr )}.\\&\parallel \\&{}^{1}\!\!/\!_{2}\end{array}}}$

Таким образом, в множестве Кантора столько же точек, сколько и в интервале [0, 1] (который имеет несчетную мощность ). Однако множество конечных точек удаленных интервалов счетно, поэтому в множестве Кантора должно быть несчетное количество чисел, которые не являются конечными точками интервала. Как отмечено выше, одним из примеров такого числа является ⁠ ${\displaystyle {\mathfrak {c}}=2^{\aleph _{0}}}$1/4⁠ , что можно записать как 0,020202... ₃ = 0, 02 в троичной системе счисления. Фактически, если задано любое , то существуют такие, что . Это было впервые продемонстрировано Штейнхаузом в 1917 году, который доказал с помощью геометрического аргумента эквивалентное утверждение, что для любого . ^[12] Поскольку эта конструкция обеспечивает инъекцию из в , мы имеем в качестве непосредственного следствия . Предполагая, что для любого бесконечного множества (утверждение, которое, как было показано, эквивалентно аксиоме выбора Тарским ), это дает еще одну демонстрацию того, что . ${\displaystyle a\in [-1,1]}$ ${\displaystyle x,y\in {\mathcal {C}}}$ ${\displaystyle a=y-x}$ ${\displaystyle \{(x,y)\in \mathbb {R} ^{2}\mid y=x+a\}\;\cap \;({\mathcal {C}}\times {\mathcal {C}})\neq \emptyset }$ ${\displaystyle a\in [-1,1]}$ ${\displaystyle [-1,1]}$ ${\displaystyle {\mathcal {C}}\times {\mathcal {C}}}$ ${\displaystyle |{\mathcal {C}}\times {\mathcal {C}}|\geq |[-1,1]|={\mathfrak {c}}}$ ${\displaystyle |A\times A|=|A|}$ ${\displaystyle A}$ ${\displaystyle |{\mathcal {C}}|={\mathfrak {c}}}$

Множество Кантора содержит столько же точек, сколько и интервал, из которого оно взято, но само не содержит интервала ненулевой длины. Иррациональные числа обладают тем же свойством, но множество Кантора имеет дополнительное свойство быть замкнутым , поэтому оно даже не плотно ни в одном интервале, в отличие от иррациональных чисел, которые плотны в каждом интервале.

Было высказано предположение , что все алгебраические иррациональные числа являются нормальными . Поскольку элементы множества Кантора не являются нормальными, это означало бы, что все элементы множества Кантора являются либо рациональными, либо трансцендентными .

Самоподобие

Множество Кантора является прототипом фрактала . Оно самоподобно , поскольку равно двум копиям самого себя, если каждую копию уменьшить в 3 раза и перенести. Точнее, множество Кантора равно объединению двух функций, левого и правого преобразований самоподобия самого себя и , которые оставляют множество Кантора инвариантным с точностью до гомеоморфизма : ${\displaystyle T_{L}(x)=x/3}$ ${\displaystyle T_{R}(x)=(2+x)/3}$ ${\displaystyle T_{L}({\mathcal {C}})\cong T_{R}({\mathcal {C}})\cong {\mathcal {C}}=T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}}).}$

Повторяющаяся итерация и может быть визуализирована как бесконечное бинарное дерево . То есть, в каждом узле дерева можно рассматривать поддерево слева или справа. Взятие множества вместе с композицией функций образует моноид , диадический моноид . ${\displaystyle T_{L}}$ ${\displaystyle T_{R}}$ ${\displaystyle \{T_{L},T_{R}\}}$

Автоморфизмы бинарного дерева являются его гиперболическими вращениями и задаются модулярной группой . Таким образом, множество Кантора является однородным пространством в том смысле, что для любых двух точек и в множестве Кантора существует гомеоморфизм с . Явную конструкцию можно описать проще , если рассматривать множество Кантора как пространство-произведение счетного числа копий дискретного пространства . Тогда отображение, определяемое как , является инволютивным гомеоморфизмом, меняющим местами и . ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle h:{\mathcal {C}}\to {\mathcal {C}}}$ ${\displaystyle h(x)=y}$ ${\displaystyle h}$ ${\displaystyle \{0,1\}}$ ${\displaystyle h:\{0,1\}^{\mathbb {N} }\to \{0,1\}^{\mathbb {N} }}$ ${\displaystyle h_{n}(u):=u_{n}+x_{n}+y_{n}\mod 2}$ ${\displaystyle x}$ ${\displaystyle y}$

Закон сохранения

Было обнаружено, что некоторая форма закона сохранения всегда отвечает за масштабирование и самоподобие. В случае множества Кантора можно увидеть, что th-й момент (где — фрактальная размерность ) всех выживших интервалов на любой стадии процесса построения равен константе, которая равна единице в случае множества Кантора. ^{[13] [14]} Мы знаем, что в системе на th-м шаге ее построения присутствуют интервалы размера . Тогда, если мы обозначим выжившие интервалы как , то th-й момент будет равен . ${\displaystyle d_{f}}$ ${\displaystyle d_{f}=\ln(2)/\ln(3)}$ ${\displaystyle N=2^{n}}$ ${\displaystyle 1/3^{n}}$ ${\displaystyle n}$ ${\displaystyle x_{1},x_{2},\ldots ,x_{2^{n}}}$ ${\displaystyle d_{f}}$ ${\displaystyle x_{1}^{d_{f}}+x_{2}^{d_{f}}+\cdots +x_{2^{n}}^{d_{f}}=1}$ ${\displaystyle x_{1}=x_{2}=\cdots =x_{2^{n}}=1/3^{n}}$

Размерность Хаусдорфа множества Кантора равна ln(2)/ln(3) ≈ 0,631.

Топологические и аналитические свойства

Хотя под «множеством Кантора» обычно понимается исходное, среднетретье множество Кантора, описанное выше, топологи часто говорят о «множестве Кантора», которое означает любое топологическое пространство , гомеоморфное (топологически эквивалентное) ему.

Как показывает приведенный выше аргумент суммирования, множество Кантора несчетно, но имеет меру Лебега 0. Поскольку множество Кантора является дополнением объединения открытых множеств , оно само является замкнутым подмножеством действительных чисел и, следовательно, полным метрическим пространством . Поскольку оно также полностью ограничено , теорема Гейне–Бореля утверждает , что оно должно быть компактным .

Для любой точки множества Кантора и любой произвольно малой окрестности этой точки существует некоторое другое число с троичной цифрой, состоящей только из нулей и двоек, а также числа, троичные цифры которых содержат единицы. Следовательно, каждая точка множества Кантора является точкой накопления (также называемой точкой кластера или предельной точкой) множества Кантора, но ни одна из них не является внутренней точкой . Замкнутое множество, в котором каждая точка является точкой накопления, также называется совершенным множеством в топологии , в то время как замкнутое подмножество интервала без внутренних точек нигде не плотно в интервале.

Каждая точка множества Кантора является также точкой накопления дополнения множества Кантора.

Для любых двух точек в множестве Кантора будет некоторая троичная цифра, где они различаются — одна будет иметь 0, а другая 2. Разделив множество Кантора на «половинки» в зависимости от значения этой цифры, мы получим разбиение множества Кантора на два замкнутых множества, которые разделяют исходные две точки. В относительной топологии на множестве Кантора точки были разделены открыто-замкнутым множеством . Следовательно, множество Кантора полностью несвязно . Как компактное полностью несвязное хаусдорфово пространство , множество Кантора является примером пространства Стоуна .

Как топологическое пространство, множество Кантора естественно гомеоморфно произведению счетного числа копий пространства , где каждая копия несет дискретную топологию . Это пространство всех последовательностей из двух цифр ${\displaystyle \{0,1\}}$

${\displaystyle 2^{\mathbb {N} }=\{(x_{n})\mid x_{n}\in \{0,1\}{\text{ for }}n\in \mathbb {N} \},}$

который также может быть отождествлен с множеством 2-адических целых чисел . Основой открытых множеств топологии произведения являются цилиндрические множества ; гомеоморфизм отображает их в топологию подпространства , которую множество Кантора наследует от естественной топологии на действительной прямой . Эта характеристика пространства Кантора как произведения компактных пространств дает второе доказательство того, что пространство Кантора компактно, с помощью теоремы Тихонова .

Из приведенной выше характеристики следует, что множество Кантора гомеоморфно целым p -адическим числам , а если из него удалить одну точку, то и p -адическим числам .

Множество Кантора является подмножеством вещественных чисел, которые являются метрическим пространством относительно обычной метрики расстояния ; поэтому само множество Кантора является метрическим пространством, используя ту же самую метрику. В качестве альтернативы можно использовать p -адическую метрику на : если даны две последовательности , расстояние между ними равно , где — наименьший индекс, такой что ; если такого индекса нет, то две последовательности одинаковы, и мы определяем расстояние как равное нулю. Эти две метрики генерируют одну и ту же топологию на множестве Кантора. ${\displaystyle 2^{\mathbb {N} }}$ ${\displaystyle (x_{n}),(y_{n})\in 2^{\mathbb {N} }}$ ${\displaystyle d((x_{n}),(y_{n}))=2^{-k}}$ ${\displaystyle k}$ ${\displaystyle x_{k}\neq y_{k}}$

Мы видели выше, что множество Кантора является полностью несвязным совершенным компактным метрическим пространством. Действительно, в некотором смысле оно является единственным: каждое непустое полностью несвязное совершенное компактное метрическое пространство гомеоморфно множеству Кантора. Подробнее о пространствах, гомеоморфных множеству Кантора, см . в разделе Пространство Кантора.

Множество Кантора иногда рассматривается как «универсальное» в категории компактных метрических пространств , поскольку любое компактное метрическое пространство является непрерывным образом множества Кантора; однако эта конструкция не является единственной, и поэтому множество Кантора не является универсальным в точном категориальном смысле. «Универсальное» свойство имеет важные приложения в функциональном анализе , где оно иногда известно как теорема о представлении для компактных метрических пространств . ^[15]

Для любого целого числа q ≥ 2 топология на группе G = Z _q ^ω (счетная прямая сумма) дискретна. Хотя двойственное по Понтрягину Γ также есть Z _q ^ω , топология Γ компактна. Видно, что Γ полностью несвязно и совершенно — таким образом, оно гомеоморфно множеству Кантора. Гомеоморфизм проще всего явно записать в случае q = 2. (См. Rudin 1962 p 40.)

Мера и вероятность

Множество Кантора можно рассматривать как компактную группу двоичных последовательностей, и как таковое оно наделено естественной мерой Хаара . При нормализации так, чтобы мера множества была равна 1, оно является моделью бесконечной последовательности подбрасываний монеты. Более того, можно показать, что обычная мера Лебега на интервале является образом меры Хаара на множестве Кантора, в то время как естественная инъекция в троичное множество является каноническим примером сингулярной меры . Можно также показать, что мера Хаара является образом любой вероятности , что делает множество Кантора в некотором роде универсальным вероятностным пространством.

В теории меры Лебега множество Кантора является примером множества, которое несчетно и имеет нулевую меру. ^[16] Напротив, множество имеет меру Хаусдорфа 1 в своей размерности log 2 / log 3. ^[17]

числа Кантора

Если мы определим число Кантора как член множества Кантора, то ^[18]

1. Каждое действительное число в диапазоне [0, 2] является суммой двух чисел Кантора.
2. Между любыми двумя числами Кантора существует число, которое не является числом Кантора.

Описательная теория множеств

Множество Кантора является разреженным множеством (или множеством первой категории) как подмножество [0,1] (хотя и не как подмножество самого себя, поскольку это пространство Бэра ). Таким образом, множество Кантора демонстрирует, что понятия «размера» в терминах мощности, меры и категории (Бэра) не обязательно должны совпадать. Как и множество , множество Кантора является «малым» в том смысле, что оно является нулевым множеством (множеством меры нуль) и является разреженным подмножеством [0,1]. Однако, в отличие от , которое счетно и имеет «малую» мощность, мощность такая же, как у [0,1], континуума , и является «большим» в смысле мощности. Фактически, также возможно построить подмножество [0,1], которое является тощим, но имеет положительную меру, и подмножество, которое не является тощим, но имеет нулевую меру: ^[19] Взяв счетное объединение «толстых» канторовых множеств меры (см. множество Смита–Вольтерры–Кантора ниже для построения), мы получаем множество , которое имеет положительную меру (равную 1), но является тощим в [0,1], поскольку каждое из них нигде не плотно. Затем рассмотрим множество . Поскольку , не может быть тощим, но поскольку , должно иметь нулевую меру. ${\displaystyle \mathbb {Q} \cap [0,1]}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle \mathbb {Q} \cap [0,1]}$ ${\displaystyle \aleph _{0}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathfrak {c}}}$ ${\displaystyle {\mathcal {C}}^{(n)}}$ ${\displaystyle \lambda =(n-1)/n}$ ${\textstyle {\mathcal {A}}:=\bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$ ${\displaystyle {\mathcal {C}}^{(n)}}$ ${\textstyle {\mathcal {A}}^{\mathrm {c} }=[0,1]\setminus \bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$ ${\displaystyle {\mathcal {A}}\cup {\mathcal {A}}^{\mathrm {c} }=[0,1]}$ ${\displaystyle {\mathcal {A}}^{\mathrm {c} }}$ ${\displaystyle \mu ({\mathcal {A}})=1}$ ${\displaystyle {\mathcal {A}}^{\mathrm {c} }}$

Варианты

Радиальный график первых десяти шагов ^[20]

Множество Смита–Вольтерра–Кантора

Вместо того, чтобы многократно удалять среднюю треть каждой части, как в наборе Кантора, мы могли бы также продолжать удалять любой другой фиксированный процент (кроме 0% и 100%) из середины. В случае, когда середина ⁠8/10⁠ интервала удаляется, мы получаем замечательно доступный случай — множество состоит из всех чисел в [0,1], которые можно записать в виде десятичной дроби, состоящей исключительно из нулей и девяток. Если на каждом этапе удаляется фиксированный процент, то предельное множество будет иметь меру ноль, поскольку длина остатка для любого такого, что . ${\displaystyle (1-f)^{n}\to 0}$ ${\displaystyle n\to \infty }$ ${\displaystyle f}$ ${\displaystyle 0<f\leq 1}$

С другой стороны, «толстые множества Кантора» положительной меры могут быть получены путем удаления меньших долей середины сегмента в каждой итерации. Таким образом, можно построить множества, гомеоморфные множеству Кантора, которые имеют положительную меру Лебега, при этом оставаясь нигде не плотными. Если интервал длины ( ) удаляется из середины каждого сегмента на n -й итерации, то общая удаленная длина составляет , а предельное множество будет иметь меру Лебега . Таким образом, в некотором смысле, множество Кантора средней трети является предельным случаем с . Если , то остаток будет иметь положительную меру с . Этот случай известен как множество Смита–Вольтерра–Кантора , которое имеет меру Лебега . ${\displaystyle r^{n}}$ ${\displaystyle r\leq 1/3}$ ${\textstyle \sum _{n=1}^{\infty }2^{n-1}r^{n}=r/(1-2r)}$ ${\displaystyle \lambda =(1-3r)/(1-2r)}$ ${\displaystyle r=1/3}$ ${\displaystyle 0<r<1/3}$ ${\displaystyle 0<\lambda <1}$ ${\displaystyle r=1/4}$ ${\displaystyle 1/2}$

Стохастическое множество Кантора

Можно изменить конструкцию множества Кантора, разделив его случайно, а не поровну. Кроме того, чтобы включить время, мы можем разделить только один из доступных интервалов на каждом шаге вместо деления всех доступных интервалов. В случае стохастического триадического множества Кантора результирующий процесс можно описать следующим уравнением скорости ^{[13] [14]}

${\displaystyle {\frac {\partial c(x,t)}{\partial t}}=-{\frac {x^{2}}{2}}c(x,t)+2\int _{x}^{\infty }(y-x)c(y,t)\,dy,}$

и для стохастического диадического множества Кантора ^[21]

${\displaystyle {{\partial c(x,t)} \over {\partial t}}=-xc(x,t)+(1+p)\int _{x}^{\infty }c(y,t)\,dy,}$

где — число интервалов размера между и . В случае триадического множества Кантора фрактальная размерность равна , что меньше, чем у его детерминированного аналога . В случае стохастического диадического множества Кантора фрактальная размерность равна , что снова меньше, чем у его детерминированного аналога . В случае стохастического диадического множества Кантора решение для демонстрирует динамическое масштабирование , поскольку его решение в долгосрочном пределе равно , где фрактальная размерность стохастического диадического множества Кантора . В любом случае, как и у триадического множества Кантора, момент th ( ) стохастического триадического и диадического множеств Кантора также являются сохраняющимися величинами. ${\displaystyle c(x,t)dx}$ ${\displaystyle x}$ ${\displaystyle x+dx}$ ${\displaystyle 0.5616}$ ${\displaystyle 0.6309}$ ${\displaystyle p}$ ${\displaystyle \ln(1+p)/\ln 2}$ ${\displaystyle c(x,t)}$ ${\displaystyle t^{-(1+d_{f})}e^{-xt}}$ ${\displaystyle d_{f}=p}$ ${\displaystyle d_{f}}$ ${\textstyle \int x^{d_{f}}c(x,t)\,dx={\text{constant}}}$

Канторовская пыль

Канторова пыль — это многомерная версия множества Кантора. Она может быть образована путем взятия конечного декартова произведения множества Кантора с самим собой, что делает его пространством Кантора . Как и множество Кантора, пыль Кантора имеет нулевую меру . ^[22]

Рекурсивная прогрессия кубов Кантора к пыли Кантора

Другой 2D-аналог множества Кантора — ковер Серпинского , где квадрат делится на девять меньших квадратов, а средний удаляется. Оставшиеся квадраты затем делятся еще на девять квадратов каждый, а средний удаляется, и так до бесконечности. ^[23] Один 3D-аналог этого — губка Менгера .

Исторические заметки

изображение второй итерации пыли Кантора в двух измерениях

изображение 4-й итерации пыли Кантора в двух измерениях

Кантор ввел то, что мы сегодня называем троичным множеством Кантора, как пример «совершенного множества точек , которое не является всюду плотным в любом интервале, каким бы малым он ни был». ^{[24] [25]} Кантор описал его в терминах троичных разложений как «множество всех действительных чисел, заданное формулой: где коэффициенты произвольно принимают два значения 0 и 2, а ряд может состоять из конечного или бесконечного числа элементов». ^[24] ${\displaystyle {\mathcal {C}}}$ ${\displaystyle {\mathcal {C}}}$ ${\displaystyle z=c_{1}/3+c_{2}/3^{2}+\cdots +c_{\nu }/3^{\nu }+\cdots }$ ${\displaystyle c_{\nu }}$

Топологическое пространство является совершенным, если все его точки являются предельными точками или, что эквивалентно, если оно совпадает со своим производным множеством . Подмножества действительной прямой, такие как , можно рассматривать как топологические пространства в топологии индуцированного подпространства. ^[7] ${\displaystyle P}$ ${\displaystyle P'}$ ${\displaystyle {\mathcal {C}}}$

Кантор пришел к изучению производных множеств благодаря своим результатам об уникальности тригонометрических рядов . ^[25] Последние во многом определили его путь к разработке абстрактной общей теории бесконечных множеств .

Бенуа Мандельброт много писал о пыли Кантора и ее связи с естественными фракталами и статистической физикой . ^[9] Он также размышлял о загадочной или даже расстраивающей природе таких структур для тех, кто находится в сообществе математиков и физиков. В «Фрактальной геометрии природы » он описал, как «Когда я начал эту тему в 1962 году, все соглашались, что пыль Кантора по крайней мере столь же чудовищна, как кривые Коха и Пеано », и добавил, что «каждый уважающий себя физик автоматически отворачивался при упоминании Кантора, готовый бежать за милю от любого, кто утверждал, что интересуется наукой». ^[9] ${\displaystyle {\mathcal {C}}}$

Смотрите также

изображение 6-й итерации пыли Кантора в двух измерениях

• Индикаторная функция множества Кантора
• Множество Смита–Вольтерра–Кантора
• Функция Кантора
• куб Кантора
• Ожерелье Антуана
• Снежинка Коха
• Веер Кнастера–Куратовского
• Список фракталов по размерности Хаусдорфа
• Последовательность Мозера–де Брейна

  

  Капитель колонны с узором, напоминающим набор Кантора, но выраженным в двоичной, а не в троичной системе. Гравюра острова Филе из «Описания Египта» Жана-Батиста Проспера Жоллуа и Эдуарда Девилье, Imprimerie Impériale, Париж, 1809-1828 гг.

Примечания

1. Смит, Генри Дж. С. (1874). «Об интегрировании разрывных функций». Труды Лондонского математического общества . Первая серия. 6 : 140–153.
2. «Канторовое множество» также было обнаружено Полем дю Буа-Реймоном (1831–1889). См. дю Буа-Реймон, Поль (1880), «Der Beweis des Fundamentalsatzes der Integralrechnung», Mathematische Annalen (на немецком языке), 16 , сноска на стр. 128. «Канторовое множество» было также открыто в 1881 году Вито Вольтеррой (1860–1940). См.: Вольтерра, Вито (1881), «Alcune osservazioni sulle funzioni punteggiate expire» [Некоторые наблюдения о точечной разрывной функции], Giornale di Matematiche (на итальянском языке), 19 : 76–86..
3. Феррейрос, Хосе (1999). Лабиринт мысли: история теории множеств и ее роль в современной математике . Базель, Швейцария: Birkhäuser Verlag. С. 162–165. ISBN 9783034850513.
4. Стюарт, Ян (26 июня 1997 г.). Играет ли Бог в кости?: Новая математика хаоса . Penguin. ISBN 0140256024.
5. Кантор, Георг (1883). «Über unendliche, Lineare Punktmannigfaltigkeiten V» [О бесконечных линейных точечных многообразиях (множествах), Часть 5]. Mathematische Annalen (на немецком языке). 21 : 545–591. дои : 10.1007/bf01446819. S2CID  121930608. Архивировано из оригинала 24 сентября 2015 г. Проверено 10 января 2011 г.
6. Пейтген, Х.-О.; Юргенс, Х.; Заупе, Д. (2004). Хаос и фракталы: новые рубежи науки (2-е изд.). Нью-Йорк, Нью-Йорк: Springer Verlag. стр. 65. ISBN 978-1-4684-9396-2.
7. Kechris, Alexander S. (1995). Классическая описательная теория множеств. Graduate Texts in Mathematics. Vol. 156. Springer New York, NY. pp. 31, 35. doi :10.1007/978-1-4612-4190-4. ISBN 978-0-387-94374-9.
8. Солтанифар, Мохсен (2006). «Другое описание семейства средних канторовских множеств». Американский журнал бакалаврских исследований . 5 (2): 9–12. doi : 10.33697/ajur.2006.014 .
9. Мандельброт, Бенуа Б. (1983). Фрактальная геометрия природы (обновленное и дополненное издание). Нью-Йорк. ISBN 0-7167-1186-9. OCLC  36720923.{{cite book}}: CS1 maint: location missing publisher (link)
10. Belcastro, Sarah-Marie; Green, Michael (январь 2001 г.), «The Cantor set contains ? Really?», The College Mathematics Journal , 32 (1): 55, doi :10.2307/2687224, JSTOR  2687224 ${\displaystyle {\tfrac {1}{4}}}$
11. Это альтернативное повторяющееся представление числа с конечной цифрой встречается в любой позиционной системе с архимедовым абсолютным значением .
12. Carothers, NL (2000). Реальный анализ . Кембридж: Cambridge University Press. стр. 31–32. ISBN 978-0-521-69624-1.
13. Крапивский, ПЛ; Бен-Наим, Э. (1994). «Мультимасштабирование в стохастических фракталах». Physics Letters A. 196 ( 3–4): 168. Bibcode :1994PhLA..196..168K. doi :10.1016/0375-9601(94)91220-3.
14. Хассан, MK; Роджерс, GJ (1995). "Модели фрагментации и стохастические фракталы". Physics Letters A. 95 ( 1): 208. Bibcode :1995PhLA..208...95H. doi :10.1016/0375-9601(95)00727-K.
15. Уиллард, Стивен (1968). Общая топология . Эддисон-Уэсли. ASIN  B0000EG7Q0.
16. Ирвин, Лора. "Теорема 36: множество Кантора является несчетным множеством с нулевой мерой". Теорема недели . Архивировано из оригинала 2016-03-15 . Получено 2012-09-27 .
17. Фальконер, К. Дж. (24 июля 1986 г.). Геометрия фрактальных множеств (PDF) . Cambridge University Press. стр. 14–15. ISBN 9780521337052.
18. Шредер, Манфред (1991). Фракталы, хаос, степенные законы: минуты из бесконечного рая . Дувр. стр. 164–165. ISBN 0486472043.
19. Гельбаум, Бернард Р. (1964). Контрпримеры в анализе . Олмстед, Джон МХ (Джон Мейгс Хаббелл), 1911-1997. Сан-Франциско: Holden-Day. ISBN 0486428753. OCLC  527671.
20. «Радиальное множество Кантора».
21. Хассан, МК; Павел, НИ; Пандит, РК; Куртс, Дж. (2014). «Диадическое множество Кантора и его кинетический и стохастический аналог». Хаос, солитоны и фракталы . 60 : 31–39. arXiv : 1401.0249 . Bibcode : 2014CSF....60...31H. doi : 10.1016/j.chaos.2013.12.010. S2CID  14494072.
22. Хельмберг, Гилберт (2007). Знакомство с фракталами. Вальтер де Грюйтер. стр. 46. ISBN 978-3-11-019092-2.
23. Хельмберг, Гилберт (2007). Знакомство с фракталами. Вальтер де Грюйтер. стр. 48. ISBN 978-3-11-019092-2.
24. Cantor, Georg (2021). ""Основания общей теории множеств: Математически-философское исследование теории бесконечности", английский перевод Джеймса Р. Мейера". www.jamesrmeyer.com . Сноска 22 в разделе 10 . Получено 16.05.2022 .
25. Fleron, Julian F. (1994). «Заметка об истории множества Кантора и функции Кантора». Mathematics Magazine . 67 (2): 136–140. doi :10.2307/2690689. ISSN  0025-570X. JSTOR  2690689.

Ссылки

• Стин, Линн Артур ; Зеебах, Дж. Артур-младший (1995) [1978]. Контрпримеры в топологии ( переиздание Дувра 1978 г.). Берлин, Нью-Йорк: Springer-Verlag . Пример 29. ISBN 978-0-486-68735-3. МР  0507446.
• Wise, Gary L.; Hall, Eric B. (1993). Контрпримеры в вероятности и реальном анализе . Нью-Йорк: Oxford University Press . Глава 1. ISBN 0-19-507068-2.
• Фалконер, К. Дж. (24 июля 1986 г.). Геометрия фрактальных множеств . Cambridge Tracts in Mathematics. Cambridge University Press . ISBN 0521337054.
• Маттила, Пертти (25 февраля 1999 г.). Геометрия множеств и мер в евклидовом пространстве: фракталы и спрямляемость . Кембриджские исследования в области высшей математики. Cambridge University Press. ISBN 0521655951.
• Маттила, Пертти (2015). Анализ Фурье и измерение Хаусдорфа . Кембриджские исследования в области высшей математики. Cambridge University Press. ISBN 9781316227619..
• Зигмунд, А. (1958). Тригонометрические ряды, т. I и II . Издательство Кембриджского университета.

Внешние ссылки

• «Множество Кантора», Энциклопедия математики , EMS Press , 2001 [1994]
• Множества Кантора и множество Кантора и функция в cut-the-knot
• Кантор Сет в Platonic Realms