Компартментальные модели в эпидемиологии

Тип математической модели, используемой для инфекционных заболеваний

Компартментные модели — это очень общий метод моделирования. Их часто применяют для математического моделирования инфекционных заболеваний . Население распределяется по отсекам с метками, например, S , I или R ( Восприимчивый , Инфекционный или Выздоровевший ). Люди могут перемещаться между отсеками. Порядок меток обычно показывает структуру потока между отсеками; например, SEIS означает «восприимчивый», «разоблаченный», «заразный», а затем снова «восприимчивый».

Зарождение таких моделей относится к началу 20-го века, причем важными работами являются работы Росса ^[1] в 1916 году, Росса и Хадсона в 1917 году, ^{[2] [3]} Кермака и Маккендрика в 1927 году, ^[4] и Кендалла в 1956 году. ^[5] Модель Рида-Фроста также была важной и широко игнорируемой предшественницей современных подходов к эпидемиологическому моделированию. ^[6]

Модели чаще всего используют обыкновенные дифференциальные уравнения (которые являются детерминистическими), но их также можно использовать со стохастической (случайной) структурой, которая более реалистична, но гораздо сложнее анализируется.

Эти модели используются для анализа динамики заболевания и оценки общего числа инфицированных, общего числа выздоровевших, а также для оценки эпидемиологических параметров, таких как базовое репродуктивное число или эффективное репродуктивное число . Такие модели могут показать, как различные меры общественного здравоохранения могут повлиять на исход эпидемии.

Модель СИР

Модель SIR ^{[7] [8] [9] [10]} является одной из самых простых секционных моделей, и многие модели являются производными от этой базовой формы. Модель состоит из трех отделений:

S : Число восприимчивых особей. Когда восприимчивый и заразный человек вступают в «инфекционный контакт», восприимчивый человек заражается болезнью и переходит в инфекционный отсек.

I : Число заразных лиц. Это лица, которые были инфицированы и способны заразить восприимчивых лиц.

R — количество удаленных (и получивших иммунитет) или умерших особей. Это лица, которые были инфицированы и либо выздоровели от болезни и попали в удаленный отсек, либо умерли. Предполагается, что число смертей незначительно по отношению к общей численности населения. Этот отсек также можно назвать « восстановленным » или « устойчивым ».

Эта модель является достаточно прогностической ^[11] для инфекционных заболеваний, которые передаются от человека к человеку и при которых выздоровление обеспечивает устойчивую устойчивость, таких как корь , эпидемический паротит и краснуха .

Моделирование пространственной модели SIR. Каждая клетка может заразить восемь своих непосредственных соседей.

Эти переменные ( S , I и R ) представляют количество людей в каждом отсеке в определенный момент времени. Чтобы представить, что количество восприимчивых, заразных и удаленных особей может меняться со временем (даже если общий размер популяции остается постоянным), мы делаем точные цифры функцией t (времени): S ( t ), I ( t ). и Р ( т ). Для конкретного заболевания в конкретной популяции эти функции могут быть разработаны с целью прогнозирования возможных вспышек и взятия их под контроль. ^[11] Обратите внимание, что в модели SIR и являются разными величинами – первая описывает количество выздоровевших при t = 0, тогда как вторая описывает отношение между частотой контактов к частоте выздоровлений. ${\displaystyle R(0)}$ ${\displaystyle R_{0}}$

Как следует из переменной функции t , модель является динамической, поскольку числа в каждом отсеке могут меняться с течением времени. Важность этого динамического аспекта наиболее очевидна при эндемическом заболевании с коротким инфекционным периодом, таком как корь в Великобритании до введения вакцины в 1968 году. Такие заболевания имеют тенденцию возникать циклами вспышек из-за изменения количества уязвимостей (S( t )) с течением времени. Во время эпидемии число восприимчивых людей быстро падает, поскольку все больше из них заражаются и, таким образом, попадают в инфекционные и удаленные отсеки. Болезнь не может вспыхнуть снова до тех пор, пока число восприимчивых людей не восстановится, например, в результате рождения потомства в восприимчивом компартменте. ^{[ нужна цитата ]}

Желтый = восприимчивый, темно-бордовый = заразный, бирюзовый = выздоровевший

Каждый член населения обычно переходит от восприимчивого к заразному состоянию к выздоровевшему. Это можно отобразить в виде блок-схемы, на которой прямоугольники обозначают различные отсеки, а стрелки — переходы между отсеками (см. диаграмму).

Блок-схема состояний в модели эпидемии SIR и скорости перехода между ними

Ставки перехода

Для полной спецификации модели стрелками должны быть указаны скорости перехода между отсеками. Предполагается, что между S и I скорость перехода равна , где – общая численность населения, – среднее количество контактов на человека за время, умноженное на вероятность передачи заболевания при контакте между восприимчивым и инфекционным субъектом, и составляет доля контактов между заразным и восприимчивым человеком, в результате которых восприимчивый человек заражается. (Математически это похоже на закон действия масс в химии, согласно которому случайные столкновения между молекулами приводят к химической реакции, а относительная скорость пропорциональна концентрации двух реагентов. ^[12] ). ${\displaystyle d(S/N)/dt=-\beta SI/N^{2}}$ ${\displaystyle N}$ ${\displaystyle \beta }$ ${\displaystyle SI/N^{2}}$

Предполагается, что между I и R скорость перехода пропорциональна числу заразных лиц, которое составляет . Если человек заразен в течение среднего периода времени , то . Это также эквивалентно предположению, что продолжительность времени пребывания человека в заразном состоянии является случайной величиной с экспоненциальным распределением . «Классическую» модель SIR можно модифицировать, используя более сложные и реалистичные распределения скорости IR-перехода (например, распределение Эрланга ). ^[13] ${\displaystyle \gamma I}$ ${\displaystyle D}$ ${\displaystyle \gamma =1/D}$

В особом случае, когда удаление из инфекционного отсека не происходит ( ), модель SIR сводится к очень простой модели SI, имеющей логистическое решение, при котором каждый человек в конечном итоге становится инфицированным. ${\displaystyle \gamma =0}$

Модель SIR без рождения и смерти

Единая реализация эпидемии SIR, полученная с помощью реализации алгоритма Гиллеспи и численного решения системы обыкновенных дифференциальных уравнений (пунктир)

Динамика эпидемии, например, гриппа , часто намного быстрее, чем динамика рождаемости и смертности, поэтому в простых компартментальных моделях рождаемость и смертность часто опускаются. Описанная выше система СИР без так называемой динамики жизнедеятельности (рождения и смерти, иногда называемой демографией) может быть выражена следующей системой обыкновенных дифференциальных уравнений : ^{[8] [14]}

${\displaystyle \left\{{\begin{aligned}&{\frac {dS}{dt}}=-\beta IS,\\[6pt]&{\frac {dI}{dt}}=\beta IS-\gamma I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\end{aligned}}\right.}$

Модель СИР

где - численность восприимчивого населения, - численность инфицированных, - численность удаленной популяции (в результате смерти или выздоровления), а - сумма этих трех показателей. ${\displaystyle S}$ ${\displaystyle I}$ ${\displaystyle R}$ ${\displaystyle N}$

Эта модель была впервые предложена Уильямом Огилви Кермаком и Андерсоном Греем Маккендриком как частный случай того, что мы теперь называем теорией Кермака-Маккендрика , и последовала за работой, которую Маккендрик проделал с Рональдом Россом . ^{[ нужна цитата ]}

Эта система нелинейна , однако ее аналитическое решение можно получить в неявном виде. ^[7] Во-первых, обратите внимание, что из:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}+{\frac {dR}{dt}}=0,}$

следует, что:

${\displaystyle S(t)+I(t)+R(t)={\text{constant}}=N,}$

выражая в математических терминах постоянство численности населения . Обратите внимание, что приведенное выше соотношение подразумевает, что нужно изучить уравнение только для двух из трех переменных. ${\displaystyle N}$

Во-вторых, отметим, что динамика инфекционного класса зависит от следующего соотношения:

${\displaystyle R_{0}={\frac {\beta }{\gamma }},}$

так называемый базовый коэффициент воспроизводства (также называемый базовым коэффициентом воспроизводства). Это соотношение рассчитывается как ожидаемое количество новых инфекций (эти новые инфекции иногда называют вторичными инфекциями) от одной инфекции в популяции, где все субъекты восприимчивы. ^{[15] [16]} Эту идею, вероятно, можно будет легче понять, если мы скажем, что типичное время между контактами составляет , а типичное время до удаления составляет . Отсюда следует, что в среднем число контактов заразного человека с окружающими до удаления инфекционного составляет: ${\displaystyle T_{c}=\beta ^{-1}}$ ${\displaystyle T_{r}=\gamma ^{-1}}$ ${\displaystyle T_{r}/T_{c}.}$

Разделив первое дифференциальное уравнение на третье, разделив переменные и проинтегрировав, получим

${\displaystyle S(t)=S(0)e^{-R_{0}(R(t)-R(0))/N},}$

где и – исходное количество соответственно восприимчивых и удаленных субъектов. Записывая начальную долю восприимчивых особей, а также долю восприимчивых и удаленных особей соответственно в пределе, который мы имеем ${\displaystyle S(0)}$ ${\displaystyle R(0)}$ ${\displaystyle s_{0}=S(0)/N}$ ${\displaystyle s_{\infty }=S(\infty )/N}$ ${\displaystyle r_{\infty }=R(\infty )/N}$ ${\displaystyle t\to \infty ,}$

${\displaystyle s_{\infty }=1-r_{\infty }=s_{0}e^{-R_{0}(r_{\infty }-r_{0})}}$

(обратите внимание, что в этом пределе инфекционный отсек опорожняется). Это трансцендентное уравнение имеет решение в терминах W -функции Ламберта ^[17] , а именно

${\displaystyle s_{\infty }=1-r_{\infty }=-R_{0}^{-1}\,W(-s_{0}R_{0}e^{-R_{0}(1-r_{0})}).}$

Это показывает, что в конце эпидемии, которая соответствует простым предположениям модели SIR, если только не все особи популяции были удалены, то некоторые из них должны оставаться восприимчивыми. Движущей силой, ведущей к прекращению эпидемии, является снижение числа заразных лиц. Эпидемия обычно не заканчивается из-за полного отсутствия восприимчивых людей. ${\displaystyle s_{0}=0}$

Роль как основного репродуктивного числа, так и начальной восприимчивости чрезвычайно велика. Фактически, если переписать уравнение для заразных лиц следующим образом:

${\displaystyle {\frac {dI}{dt}}=\left(R_{0}{\frac {S}{N}}-1\right)\gamma I,}$

получается, что если:

${\displaystyle R_{0}\cdot S(0)>N,}$

затем:

${\displaystyle {\frac {dI}{dt}}(0)>0,}$

т. е. произойдет собственно эпидемическая вспышка с увеличением числа заразных (которые могут охватить значительную часть населения). Напротив, если

${\displaystyle R_{0}\cdot S(0)<N,}$

затем

${\displaystyle {\frac {dI}{dt}}(0)<0,}$

т.е. независимо от первоначальной численности восприимчивого населения болезнь никогда не может вызвать настоящую эпидемическую вспышку. Как следствие, ясно, что как базовое воспроизводственное число, так и начальная восприимчивость имеют чрезвычайно важное значение.

Сила заражения

Обратите внимание, что в приведенной выше модели функция:

${\displaystyle F=\beta I,}$

моделирует скорость перехода из отсека восприимчивых людей в отсек заразных особей, так что это называется силой заражения . Однако для больших классов инфекционных болезней более реалистично считать силу заражения, зависящую не от абсолютного числа заразных лиц, а от их доли (по отношению к общей постоянной численности населения ): ${\displaystyle N}$

${\displaystyle F=\beta {\frac {I}{N}}.}$

Капассо ^[18] , а затем и другие авторы предложили нелинейные силы заражения для более реалистичного моделирования процесса заражения.

Точные аналитические решения модели SIR.

В 2014 году Харко и соавторы получили точное так называемое аналитическое решение (включающее интеграл, который можно вычислить только численно) для модели SIR. ^[7] В случае без настройки динамики жизнедеятельности, при и т.д. это соответствует следующей временной параметризации ${\displaystyle {\mathcal {S}}(u)=S(t)}$

${\displaystyle {\mathcal {S}}(u)=S(0)u}$

${\displaystyle {\mathcal {I}}(u)=N-{\mathcal {R}}(u)-{\mathcal {S}}(u)}$

${\displaystyle {\mathcal {R}}(u)=R(0)-\rho \ln(u)}$

для

${\displaystyle t={\frac {N}{\beta }}\int _{u}^{1}{\frac {du^{*}}{u^{*}{\mathcal {I}}(u^{*})}},\quad \rho ={\frac {\gamma N}{\beta }},}$

с начальными условиями

${\displaystyle ({\mathcal {S}}(1),{\mathcal {I}}(1),{\mathcal {R}}(1))=(S(0),N-R(0)-S(0),R(0)),\quad u_{T}<u<1,}$

где удовлетворяет . Из трансцендентного уравнения, приведенного выше, следует, что , если и . ${\displaystyle u_{T}}$ ${\displaystyle {\mathcal {I}}(u_{T})=0}$ ${\displaystyle R_{\infty }}$ ${\displaystyle u_{T}=e^{-(R_{\infty }-R(0))/\rho }(=S_{\infty }/S(0)}$ ${\displaystyle S(0)\neq 0)}$ ${\displaystyle I_{\infty }=0}$

Эквивалентное так называемое аналитическое решение (включающее интеграл, который можно вычислить только численно), найденное Миллером ^{[19] [20]} , дает

${\displaystyle {\begin{aligned}S(t)&=S(0)e^{-\xi (t)}\\[8pt]I(t)&=N-S(t)-R(t)\\[8pt]R(t)&=R(0)+\rho \xi (t)\\[8pt]\xi (t)&={\frac {\beta }{N}}\int _{0}^{t}I(t^{*})\,dt^{*}\end{aligned}}}$

Здесь можно интерпретировать ожидаемое количество передач, полученных индивидуумом за определенное время . Два решения связаны соотношением . ${\displaystyle \xi (t)}$ ${\displaystyle t}$ ${\displaystyle e^{-\xi (t)}=u}$

Фактически тот же результат можно найти в оригинальной работе Кермака и Маккендрика. ^[4]

Эти решения можно легко понять, заметив, что все члены в правых частях исходных дифференциальных уравнений пропорциональны . Таким образом, уравнения можно разделить на , а время масштабировать так, чтобы дифференциальный оператор в левой части стал просто , где , т.е. Все дифференциальные уравнения теперь являются линейными, а третье уравнение формы const. показывает, что и (и выше) просто линейно связаны. ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle d/d\tau }$ ${\displaystyle d\tau =Idt}$ ${\displaystyle \tau =\int Idt}$ ${\displaystyle dR/d\tau =}$ ${\displaystyle \tau }$ ${\displaystyle R}$ ${\displaystyle \xi }$

Высокоточная аналитическая аппроксимация модели SIR, а также точные аналитические выражения для конечных значений , и были предоставлены Крёгером и Шликкейзером ^[9] , так что нет необходимости выполнять численное интегрирование для решения модели SIR (а упрощенный пример практики численного моделирования COVID-19 с использованием Microsoft Excel можно найти здесь ^[21] ), чтобы получить его параметры из существующих данных или спрогнозировать будущую динамику эпидемии, смоделированной с помощью модели SIR. Аппроксимант включает в себя функцию Ламберта W , которая является частью всех базовых программ визуализации данных, таких как Microsoft Excel, MATLAB и Mathematica . ${\displaystyle S_{\infty }}$ ${\displaystyle I_{\infty }}$ ${\displaystyle R_{\infty }}$

В то время как Кендалл ^[5] рассматривал так называемую модель SIR за все время, в которой начальные условия , и связаны указанными выше соотношениями, Кермак и МакКендрик ^[4] предложили изучить более общий полувременной случай, для которого и оба произвольны. Эта последняя версия, обозначенная как полувременная модель SIR, ^[9] делает прогнозы только на будущее время . Аналитическая аппроксимация и точные выражения для конечных значений также доступны для полувременной модели SIR. ^[10] ${\displaystyle S(0)}$ ${\displaystyle I(0)}$ ${\displaystyle R(0)}$ ${\displaystyle S(0)}$ ${\displaystyle I(0)}$ ${\displaystyle t>0}$

Численные решения модели SIR с аппроксимациями

Численные решения модели SIR можно найти в литературе. Примером может служить использование модели для анализа данных о распространении COVID-19 . ^{[21] [22]} Из данных, проанализированных с помощью числовой аппроксимации, можно получить три числа воспроизводства:

основной номер воспроизводства :

${\displaystyle R_{0}={\frac {\beta _{0}}{\gamma _{0}}}}$

номер воспроизведения в реальном времени:

${\displaystyle R_{t}={\frac {\beta _{t}}{\gamma _{t}}}}$

и эффективное число воспроизводства в реальном времени:

${\displaystyle R_{e}={\frac {\beta _{t}S}{\gamma _{t}N}}}$

${\displaystyle R_{0}}$представляет собой скорость воспроизводства в начале распространения, когда все популяции считаются восприимчивыми, например, если и означает, что один заразный человек в среднем заражает 0,4 восприимчивых человека в день и выздоравливает за 1/0,2 = 5 дней. Таким образом, когда этот человек выздоровел, осталось еще два человека, заразных непосредственно от этого человека, т.е. количество заразных людей удвоилось за один цикл из 5 дней. Данные, смоделированные с помощью модели или подогнанные реальные данные, приведут к удвоению числа заразных людей быстрее, чем за 5 дней, поскольку два инфицированных человека заражают людей. Из модели SIR мы можем сказать, что это определяется характером заболевания, а также функцией частоты взаимодействия между заразным человеком и восприимчивыми людьми , а также интенсивностью/продолжительностью взаимодействия, например, насколько близко они взаимодействуют и как долго. и носят ли они оба маски или нет, таким образом, это меняется со временем, когда меняется среднее поведение носителей и восприимчивых людей. Модель используется для представления этих факторов, но на самом деле она относится к начальному этапу, когда не предпринимается никаких действий для предотвращения распространения и все население восприимчиво, поэтому все изменения поглощаются изменением . ${\displaystyle \beta _{0}=0.4day^{-1}}$ ${\displaystyle \gamma _{0}=0.2day^{-1}}$ ${\displaystyle R_{0}=2}$ ${\displaystyle R_{0}=2}$ ${\displaystyle \beta }$ ${\displaystyle I}$ ${\displaystyle S}$ ${\displaystyle SI}$ ${\displaystyle \beta }$

${\displaystyle \gamma }$обычно более стабилен с течением времени, если предположить, что когда у заразного человека появятся симптомы, он/она обратится за медицинской помощью или будет самоизолирован. Поэтому, если мы обнаружим изменения, скорее всего, поведение людей в обществе изменилось по сравнению с их обычным поведением до вспышки, или болезнь мутировала в новую форму. Затратное массовое обнаружение и изоляция уязвимых близких контактов оказывают влияние на сокращение, но эффективность этого вопроса обсуждается. Эти дебаты в основном ведутся вокруг неопределенности количества дней, прошедших после заражения или обнаружения, в зависимости от того, что наступит раньше, до появления симптомов у инфицированного восприимчивого человека. Если человек заразен после появления симптомов или обнаружение работает только для человека с симптомами, то в этих методах профилактики нет необходимости, а самоизоляция и/или медицинская помощь являются лучшим способом снизить показатели . Типичное начало инфекционного периода COVID-19 происходит примерно через один день после появления симптомов, что делает бесполезным массовое выявление с типичной частотой в несколько дней. ${\displaystyle R_{t}}$ ${\displaystyle 1/\gamma }$ ${\displaystyle 1/\gamma }$

${\displaystyle R_{t}}$не говорит нам, ускорится или замедлится распространение на последних стадиях, когда доля восприимчивых людей в обществе значительно сократится после выздоровления или вакцинации. этот эффект разбавления корректируется путем умножения доли восприимчивой популяции на общую численность населения. Он корректирует эффективное/передаваемое взаимодействие между заразным человеком и остальной частью сообщества, когда многие из взаимодействий являются невосприимчивыми на средних и поздних стадиях распространения заболевания. Таким образом, когда мы увидим экспоненциальную вспышку; когда достигается устойчивое состояние и количество заразных людей с течением времени не меняется; а когда болезнь ослабевает и со временем исчезает. ${\displaystyle R_{e}}$ ${\displaystyle R_{e}>1}$ ${\displaystyle R_{e}=1}$ ${\displaystyle R_{e}<1}$

Используя дифференциальные уравнения модели SIR и преобразовывая их в числовые дискретные формы, можно составить рекурсивные уравнения и рассчитать популяции S, I и R с любыми заданными начальными условиями, но накапливать ошибки в течение длительного времени расчета от контрольной точки. . Иногда для оценки ошибок необходим тест сходимости . Учитывая набор начальных условий и данные о распространении болезни, можно также согласовать данные с моделью SIR и получить три числа воспроизводства, когда ошибки обычно незначительны из-за короткого временного шага от контрольной точки. ^{[21] [22]} Любой момент времени может использоваться в качестве начального условия для прогнозирования будущего после него с использованием этой числовой модели с предположением изменяющихся во времени параметров, таких как численность населения, и . Однако за пределами этой контрольной точки ошибки со временем будут накапливаться, поэтому необходим тест сходимости, чтобы найти оптимальный временной шаг для получения более точных результатов. ${\displaystyle R_{t}}$ ${\displaystyle \gamma }$

Среди этих трех показателей воспроизводства очень полезно судить о контрольном давлении, например, большое значение означает, что болезнь будет распространяться очень быстро и ее очень трудно контролировать. наиболее полезен для прогнозирования будущих тенденций, например, если мы знаем, что количество социальных взаимодействий часто сокращается на 50% по сравнению с тем, что было до вспышки, и интенсивность взаимодействия между людьми остается такой же, тогда мы можем установить . Если социальное дистанцирование и маски добавят еще 50% снижения эффективности заражения, мы сможем установить . будет идеально коррелировать с волнами распространения, и когда распространение ускоряется, а когда распространение замедляется, это полезно для прогнозирования краткосрочных тенденций. Кроме того, его можно использовать для непосредственного расчета пороговой популяции вакцинации/иммунизации для стадии коллективного иммунитета, установив , и , т.е. ${\displaystyle R_{0}}$ ${\displaystyle R_{t}}$ ${\displaystyle R_{t}=0.5R_{0}}$ ${\displaystyle R_{t}=0.25R_{0}}$ ${\displaystyle R_{e}}$ ${\displaystyle R_{e}>1}$ ${\displaystyle R_{e}<1}$ ${\displaystyle R_{t}=R_{0}}$ ${\displaystyle R_{E}=1}$ ${\displaystyle S=N/R_{0}}$

Модель SIR с динамикой жизнедеятельности и постоянной численностью населения

Рассмотрим популяцию, характеризующуюся уровнем смертности и рождаемости , и в которой распространяется инфекционное заболевание. ^[8] Модель с трансмиссией массового действия: ${\displaystyle \mu }$ ${\displaystyle \Lambda }$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dI}{dt}}&={\frac {\beta IS}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

для которого безболезненное равновесие (DFE) равно:

${\displaystyle \left(S(t),I(t),R(t)\right)=\left({\frac {\Lambda }{\mu }},0,0\right).}$

В этом случае мы можем получить базовое число воспроизводства :

${\displaystyle R_{0}={\frac {\beta }{\mu +\gamma }},}$

который имеет пороговые свойства. Фактически, независимо от биологически значимых начальных значений, можно показать, что:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {DFE}}=\left({\frac {\Lambda }{\mu }},0,0\right)}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(S(t),I(t),R(t))={\textrm {EE}}=\left({\frac {\gamma +\mu }{\beta }},{\frac {\mu }{\beta }}\left(R_{0}-1\right),{\frac {\gamma }{\beta }}\left(R_{0}-1\right)\right).}$

Точка ЭЭ называется эндемическим равновесием (болезнь не искоренена полностью и сохраняется в популяции). Используя эвристические аргументы, можно показать, что это можно понимать как среднее количество инфекций, вызванных одним инфекционным субъектом в полностью восприимчивой популяции. Вышеупомянутая связь с биологической точки зрения означает, что если это число меньше или равно единице, болезнь вымирает. тогда как, если это число больше единицы, болезнь останется навсегда эндемической среди населения. ${\displaystyle R_{0}}$

Модель СИР

Диаграмма модели SIR с начальными значениями , показателями заражения и выздоровления. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \beta =0.4}$ ${\textstyle \gamma =0.04}$

Анимация модели SIR с начальными значениями и скоростью восстановления . На анимации показан эффект снижения уровня заражения с до . Если нет доступных лекарств или вакцинации, снизить уровень заражения (часто называемое « сглаживанием кривой ») можно только с помощью соответствующих мер, таких как социальное дистанцирование. ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \gamma =0.04}$ ${\textstyle \beta =0.5}$ ${\textstyle \beta =0.12}$

В 1927 году У. О. Кермак и А. Г. Маккендрик создали модель, в которой они рассматривали фиксированную популяцию только с тремя компартментами: восприимчивая, ; зараженный, ; и выздоровел, . Отсеки, используемые в этой модели, состоят из трех классов: ^[4] ${\displaystyle S(t)}$ ${\displaystyle I(t)}$ ${\displaystyle R(t)}$

• ${\displaystyle S(t)}$используется для обозначения лиц, еще не инфицированных этим заболеванием на момент времени t, или восприимчивых к заболеванию населения.
• ${\displaystyle I(t)}$обозначает лиц из населения, которые были инфицированы этим заболеванием и способны распространить заболевание среди лиц, относящихся к восприимчивой категории.
• ${\displaystyle R(t)}$— это отсек, используемый для лиц из популяции, которые были инфицированы, а затем выздоровели от болезни либо в результате иммунизации, либо в результате смерти. Люди из этой категории не могут заразиться повторно или передать инфекцию другим.

Поток этой модели можно рассматривать следующим образом:

${\displaystyle {\color {blue}{{\mathcal {S}}\rightarrow {\mathcal {I}}\rightarrow {\mathcal {R}}}}}$

Использование фиксированной совокупности в трех функциях решает, что значение должно оставаться постоянным в рамках моделирования, если моделирование используется для решения модели SIR. В качестве альтернативы можно использовать аналитический аппроксимант ^[9] без проведения моделирования. Модель запускается со значениями , и . Это количество людей в категориях восприимчивых, зараженных и удаленных на момент времени равное нулю. Если предполагается, что модель SIR выполняется всегда, эти начальные условия не являются независимыми. ^[9] Впоследствии модель потока обновляет три переменные для каждого момента времени с заданными значениями для и . Моделирование сначала обновляет зараженную категорию восприимчивой, а затем удаленную категорию обновляет зараженную категорию для следующего момента времени (t=1). Это описывает поток людей между тремя категориями. Во время эпидемии категория восприимчивости не меняется в соответствии с этой моделью, а меняется в ходе эпидемии, как и . Эти переменные определяют продолжительность эпидемии, и их необходимо обновлять с каждым циклом. ${\displaystyle N=S(t)+I(t)+R(t)}$ ${\displaystyle N}$ ${\displaystyle S(t=0)}$ ${\displaystyle I(t=0)}$ ${\displaystyle R(t=0)}$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$

${\displaystyle {\frac {dS}{dt}}=-\beta SI}$

${\displaystyle {\frac {dI}{dt}}=\beta SI-\gamma I}$

${\displaystyle {\frac {dR}{dt}}=\gamma I}$

При формулировке этих уравнений было сделано несколько допущений: во-первых, следует считать, что человек в популяции имеет равную вероятность, как и любой другой человек, заразиться этим заболеванием с частотой и равной долей людей, с которыми этот человек вступает в контакт. в единицу времени. Тогда пусть будет произведением и . Это вероятность передачи, умноженная на частоту контактов. Кроме того, инфицированный человек вступает в контакт с людьми в единицу времени, тогда как восприимчивой является лишь часть из них. Таким образом, мы имеем, что каждый инфекционный агент может заразить восприимчивых лиц, и, следовательно, целое число восприимчивых, зараженных инфекционными агентами в единицу времени, равно . Для второго и третьего уравнений считайте, что численность населения, покидающего восприимчивый класс, равна числу людей, попадающих в зараженный класс. Однако количество, равное доле (которая представляет собой средний уровень выздоровления/смертности или средний период заражения) заразных лиц, покидает этот класс в единицу времени и попадает в удаленный класс. Эти процессы, происходящие одновременно, называются законом действия масс — широко распространенной идеей, согласно которой скорость контактов между двумя группами населения пропорциональна размеру каждой из соответствующих групп. Наконец, предполагается, что скорость заражения и выздоровления намного быстрее, чем временной масштаб рождаемости и смертности, и поэтому эти факторы в этой модели игнорируются. ^[23] ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle \beta }$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle b}$ ${\displaystyle S/N}$ ${\displaystyle abS=\beta S}$ ${\displaystyle \beta SI}$ ${\displaystyle \gamma }$ ${\displaystyle 1/\gamma }$

Стационарные решения

Ожидаемая продолжительность восприимчивости будет отражать время жизни (ожидаемую продолжительность жизни) и время нахождения в восприимчивом состоянии до заражения, что можно упростить ^[24] до: ${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]}$ ${\displaystyle T_{L}}$ ${\displaystyle T_{S}}$

${\displaystyle \operatorname {E} [\min(T_{L}\mid T_{S})]=\int _{0}^{\infty }e^{-(\mu +\delta )x}\,dx={\frac {1}{\mu +\delta }},}$

таким образом, что число восприимчивых лиц равно числу людей, вошедших в восприимчивый компартмент, умноженному на продолжительность восприимчивости: ${\displaystyle \mu N}$

${\displaystyle S={\frac {\mu N}{\mu +\lambda }}.}$

Аналогично, устойчивое число инфицированных — это количество людей, перешедших в инфицированное состояние из восприимчивого состояния (число восприимчивых, умноженное на скорость заражения), умноженное на продолжительность заразности : ${\displaystyle \lambda ={\tfrac {\beta I}{N}},}$ ${\displaystyle {\tfrac {1}{\mu +v}}}$

${\displaystyle I={\frac {\mu N}{\mu +\lambda }}\lambda {\frac {1}{\mu +v}}.}$

Другие купейные модели

Существует множество модификаций модели SIR, в том числе те, которые включают рождения и смерти, где при выздоровлении иммунитет отсутствует (модель SIS), где иммунитет сохраняется лишь в течение короткого периода времени (SIRS), где имеется латентный период заболевание, при котором человек не заразен (SEIS и SEIR) и при котором дети могут рождаться с иммунитетом (MSIR). Компартментальные модели также можно использовать для моделирования нескольких групп риска и даже взаимодействия нескольких патогенов. ^[25]

Вариации базовой модели SIR

Модель СИС

Желтый = восприимчивый, темно-бордовый = зараженный

Некоторые инфекции, например простуда и грипп , не дают длительного иммунитета. Такие инфекции могут давать временную устойчивость, но не дают долговременного иммунитета после выздоровления, и люди снова становятся восприимчивыми.

Отсекальная модель SIS

У нас есть модель:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=-{\frac {\beta SI}{N}}+\gamma I\\[6pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I\end{aligned}}}$

Обратите внимание, что, обозначая N общую численность населения, считается, что:

${\displaystyle {\frac {dS}{dt}}+{\frac {dI}{dt}}=0\Rightarrow S(t)+I(t)=N}$.

Следует, что:

${\displaystyle {\frac {dI}{dt}}=(\beta -\gamma )I-{\frac {\beta }{N}}I^{2}}$,

т.е. динамикой инфекционных заболеваний управляет логистическая функция , так что : ${\displaystyle \forall I(0)>0}$

${\displaystyle {\begin{aligned}&{\frac {\beta }{\gamma }}\leq 1\Rightarrow \lim _{t\to +\infty }I(t)=0,\\[6pt]&{\frac {\beta }{\gamma }}>1\Rightarrow \lim _{t\to +\infty }I(t)=\left(1-{\frac {\gamma }{\beta }}\right)N.\end{aligned}}}$

Можно найти аналитическое решение этой модели (сделав преобразование переменных и подставив его в уравнения среднего поля) ^[26] такое, что базовая скорость воспроизводства будет больше единицы. Решение дается как ${\displaystyle I=y^{-1}}$

${\displaystyle I(t)={\frac {I_{\infty }}{1+Ve^{-\chi t}}}}$.

где эндемичная инфекционная популяция, , и . Поскольку предполагается, что система закрыта, восприимчивая популяция составляет . ${\displaystyle I_{\infty }=(1-\gamma /\beta )N}$ ${\displaystyle \chi =\beta -\gamma }$ ${\displaystyle V=I_{\infty }/I_{0}-1}$ ${\displaystyle S(t)=N-I(t)}$

Всякий раз, когда очевиден целочисленный характер числа возбудителей (популяции с численностью менее десятков тысяч особей), присущие колебания процесса распространения заболевания, вызванные дискретными возбудителями, приводят к неопределенностям. ^[27] В этом сценарии эволюция заболевания, предсказанная уравнениями компартментов, значительно отклоняется от наблюдаемых результатов. Эти неопределенности могут даже привести к тому, что эпидемия закончится раньше, чем предсказывают отдельные уравнения.

В частном случае можно получить обычную логистическую функцию, полагая . Это также можно учесть в модели SIR с , т.е. никакого удаления не произойдет. Это модель SI . ^[28] Таким образом , система дифференциальных уравнений сводится к: ${\displaystyle \gamma =0}$ ${\displaystyle R=0}$ ${\displaystyle S=N-I}$

${\displaystyle {\frac {dI}{dt}}\propto I\cdot (N-I).}$

В долгосрочной перспективе в модели SI все люди заразятся.

Модель SIRD

Диаграмма модели SIRD с начальными значениями и показателями заражения , выздоровления и смертности ${\displaystyle S(0)=997,I(0)=3,R(0)=0}$ ${\displaystyle \beta =0.4}$ ${\displaystyle \gamma =0.035}$ ${\displaystyle \mu =0.005}$

Анимация модели SIRD с начальными значениями , показателями выздоровления и смертности . На анимации показан эффект снижения уровня заражения с до . Если нет доступных лекарств или вакцинации, снизить уровень заражения (часто называемое «сглаживанием кривой») можно только с помощью таких мер, как «социальное дистанцирование». ${\textstyle S(0)=997,I(0)=3,R(0)=0}$ ${\textstyle \gamma =0.035}$ ${\textstyle \mu =0.005}$ ${\textstyle \beta =0.5}$ ${\textstyle \beta =0.12}$

Модель « Восприимчивый-Инфекционный-Выздоровевший-Умерший» различает «Выздоровевших» (имеются в виду конкретно люди, пережившие болезнь и теперь обладающие иммунитетом) и «Умерших» . ^[15] Модель SIRD имеет полуаналитические решения, основанные на методе четырех частей. ^[29] В этой модели используется следующая система дифференциальных уравнений:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta IS}{N}},\\[6pt]&{\frac {dI}{dt}}={\frac {\beta IS}{N}}-\gamma I-\mu I,\\[6pt]&{\frac {dR}{dt}}=\gamma I,\\[6pt]&{\frac {dD}{dt}}=\mu I,\end{aligned}}}$

где темпы заражения, выздоровления и смертности соответственно. ^[30] ${\displaystyle \beta ,\gamma ,\mu }$

Модель SIRV

Модель «Восприимчивые-инфекционные-выздоровевшие-вакцинированные» представляет собой расширенную модель SIR, учитывающую вакцинацию восприимчивого населения. ^[31] В этой модели используется следующая система дифференциальных уравнений:

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-{\frac {\beta (t)IS}{N}}-v(t)S,\\[6pt]&{\frac {dI}{dt}}={\frac {\beta (t)IS}{N}}-\gamma (t)I,\\[6pt]&{\frac {dR}{dt}}=\gamma (t)I,\\[6pt]&{\frac {dV}{dt}}=v(t)S,\end{aligned}}}$

Мультик для модели SIRV

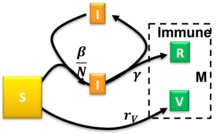
где показатели заражения, выздоровления и вакцинации соответственно. Для полувременных начальных условий , , и постоянных отношений модель была решена приближенно. ^[31] Для возникновения пандемической вспышки необходимо и существует критическое снижение уровня вакцинации, за пределами которого устойчивый размер восприимчивого компартмента остается относительно близким к . Произвольные начальные условия, удовлетворяющие, могут быть сопоставлены с решенным частным случаем с помощью . ^[31] ${\displaystyle \beta ,\gamma ,v}$ ${\displaystyle S(0)=(1-\eta )N}$ ${\displaystyle I(0)=\eta N}$ ${\displaystyle R(0)=V(0)=0}$ ${\displaystyle k=\gamma (t)/\beta (t)}$ ${\displaystyle b=v(t)/\beta (t)}$ ${\displaystyle k+b<1-2\eta }$ ${\displaystyle b_{c}}$ ${\displaystyle S_{\infty }}$ ${\displaystyle S(0)}$ ${\displaystyle S(0)+I(0)+R(0)+V(0)=N}$ ${\displaystyle R(0)=V(0)=0}$

Численное решение этой модели для расчета коэффициента воспроизводства COVID-19 в реальном времени можно применять на практике на основе информации, полученной от различных групп населения в сообществе. ^[22] Численное решение — это широко используемый метод анализа сложных кинетических сетей, когда аналитическое решение трудно получить или оно ограничено такими требованиями, как граничные условия или специальные параметры. Он использует рекурсивные уравнения для расчета следующего шага путем преобразования численного интегрирования в сумму Римана дискретных временных шагов, например, использование вчерашней основной суммы долга и процентной ставки для расчета сегодняшних процентов, что предполагает, что процентная ставка фиксирована в течение дня. Расчет содержит прогнозируемые ошибки, если не включены аналитические поправки к размеру числового шага, например, когда процентная ставка годового сбора упрощается до 12-кратной месячной ставки, возникает прогнозируемая ошибка. Таким образом, результаты расчетов будут нести накопительные ошибки, когда временной шаг находится далеко от контрольной точки, и для оценки ошибки необходим тест сходимости . Однако эта ошибка обычно приемлема для подбора данных. При подборе набора данных с близким шагом по времени ошибка относительно невелика, поскольку контрольная точка находится рядом по сравнению с прогнозированием длительного периода времени после контрольной точки. Как только изображение реального времени будет извлечено, его можно будет сравнить с базовым числом воспроизведения . Перед вакцинацией дает политикам и широкой общественности меру эффективности мер по смягчению социальных последствий, таких как социальное дистанцирование и ношение масок, просто путем деления . При массовой вакцинации целью борьбы с болезнью является снижение эффективного репродуктивного числа , где – численность восприимчивого населения в данный момент, – общая численность населения. Когда , распространение затухает, и ежедневные случаи заражения снижаются. ${\displaystyle R_{t}}$ ${\displaystyle R_{t}}$ ${\displaystyle R_{0}}$ ${\displaystyle R_{t}}$ ${\displaystyle {\frac {R_{t}}{R_{0}}}}$ ${\displaystyle R_{e}={\frac {R_{t}S}{N}}<1}$ ${\displaystyle S}$ ${\displaystyle N}$ ${\displaystyle R_{e}<1}$

Модель SIRVD

Модель эпидемического отсека « восприимчивые инфицированные-выздоровевшие-вакцинированные-умершие» (SIRVD) расширяет модель SIR, включив в нее влияние кампаний вакцинации и зависящие от времени показатели смертности при эпидемических вспышках. Он включает в себя модели SIR, SIRV, SIRD и SI как особые случаи, с индивидуальными, зависящими от времени скоростями, управляющими переходами между различными фракциями. ^[32] Эта модель использует следующую систему дифференциальных уравнений для долей населения : ${\displaystyle S,I,R,V,D}$

В этом файле представлено изображение модели SIRVD.

${\displaystyle {\begin{aligned}&{\frac {dS}{dt}}=-a(t)SI-v(t)S,\\[6pt]&{\frac {dI}{dt}}=a(t)SI-\mu (t)I-\psi (t)I,\\[6pt]&{\frac {dR}{dt}}=\mu (t)I,\\[6pt]&{\frac {dV}{dt}}=v(t)S,\\[6pt]&{\frac {dD}{dt}}=\psi (t)I\end{aligned}}}$

где показатели инфицирования, вакцинации, выздоровления и смертности соответственно. Для полувременных начальных условий , , и постоянных отношений , , модель была решена приближенно и точно для некоторых частных случаев, независимо от функциональной формы . ^[32] Это достигается путем переписывания приведенных выше уравнений модели SIRVD в эквивалентной, но сокращенной форме. ${\displaystyle a(t),v(t),\mu (t),\psi (t)}$ ${\displaystyle S(0)=1-\eta }$ ${\displaystyle I(0)=\eta }$ ${\displaystyle R(0)=V(0)=D(0)=0}$ ${\displaystyle k=\mu (t)/a(t)}$ ${\displaystyle b=v(t)/a(t)}$ ${\displaystyle q=\psi (t)/a(t)}$ ${\displaystyle a(t)}$

${\displaystyle {\begin{aligned}&{\frac {dS}{d\tau }}=-SI-b(\tau )S,\\[6pt]&{\frac {dI}{d\tau }}=SI-[k(\tau )+q(\tau )]I,\\[6pt]&{\frac {dR}{d\tau }}=k(\tau )I,\\[6pt]&{\frac {dV}{d\tau }}=b(\tau )S,\\[6pt]&{\frac {dD}{d\tau }}=q(\tau )S\end{aligned}}}$

где

${\displaystyle \tau (t)=\int _{0}^{t}a(\xi )d\xi }$

представляет собой сокращенное, безразмерное время. Временная зависимость доли инфицированных и уровня новых инфекций различается при рассмотрении эффектов вакцинации и при расхождении зависимости показателей смертности и выздоровления в реальном времени. Эти различия были подчеркнуты для стационарных коэффициентов и постепенного снижения уровня смертности. ^[32] Случай стационарных соотношений позволяет построить метод диагностики для аналитического извлечения всех параметров модели SIRVD из измеренных данных о COVID-19 завершенной волны пандемии. ^[32] ${\displaystyle I(\tau )}$ ${\displaystyle j(\tau )=S(\tau )I(\tau )}$

Модель MSIR

При многих инфекциях, включая корь , дети не рождаются в восприимчивом отделе, но имеют иммунитет к заболеванию в течение первых нескольких месяцев жизни благодаря защите материнских антител (передаваемых через плаценту и , дополнительно, через молозиво ). Это называется пассивный иммунитет . Эту дополнительную информацию можно продемонстрировать, включив в начало модели класс М (для иммунитета, полученного по материнской линии).

Модель отсека MSIR

Чтобы указать это математически, добавляется дополнительный отсек M ( t ) . Это приводит к следующим дифференциальным уравнениям:

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[8pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[8pt]{\frac {dI}{dt}}&={\frac {\beta SI}{N}}-\gamma I-\mu I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

Государство-перевозчик

Некоторые люди, перенесшие инфекционное заболевание, такое как туберкулез, никогда полностью не выздоравливают и продолжают переносить инфекцию, хотя сами не страдают этим заболеванием. Затем они могут вернуться в инфекционный отсек и страдать от симптомов (как при туберкулезе) или могут продолжать заражать других в состоянии носителя, не испытывая при этом симптомов. Самым известным примером этого, вероятно, является Мэри Мэллон , которая заразила брюшным тифом 22 человека . Багажное отделение имеет маркировку C.

Модель SEIR

Для многих важных инфекций существует значительный латентный период, в течение которого люди инфицированы, но сами еще не заразны. В этот период человек находится в отсеке Е (для облученных).

Модель отсека SEIR

Предполагая, что латентный период является случайной величиной с экспоненциальным распределением по параметру (т.е. средний латентный период равен ), а также предполагая наличие динамики жизнедеятельности с уровнем рождаемости , равным уровню смертности (так что общее число постоянно), мы имеем модель: ${\displaystyle a}$ ${\displaystyle a^{-1}}$ ${\displaystyle \Lambda }$ ${\displaystyle N\mu }$ ${\displaystyle N}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-{\frac {\beta IS}{N}}\\[8pt]{\frac {dE}{dt}}&={\frac {\beta IS}{N}}-(\mu +a)E\\[8pt]{\frac {dI}{dt}}&=aE-(\gamma +\mu )I\\[8pt]{\frac {dR}{dt}}&=\gamma I-\mu R.\end{aligned}}}$

Есть , но это константа только из-за упрощающего предположения, что уровни рождаемости и смертности равны; вообще это переменная. ${\displaystyle S+E+I+R=N,}$ ${\displaystyle N}$

Для этой модели базовый номер репродукции:

${\displaystyle R_{0}={\frac {a}{\mu +a}}{\frac {\beta }{\mu +\gamma }}.}$

Подобно модели SIR, в этом случае мы также имеем равновесие без болезней ( N ,0,0,0) и эндемическое равновесие EE, и можно показать, что независимо от биологически значимых начальных условий

${\displaystyle \left(S(0),E(0),I(0),R(0)\right)\in \left\{(S,E,I,R)\in [0,N]^{4}:S\geq 0,E\geq 0,I\geq 0,R\geq 0,S+E+I+R=N\right\}}$

он утверждает, что:

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=DFE=(N,0,0,0),}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),E(t),I(t),R(t)\right)=EE.}$

В случае периодически меняющейся скорости контакта условием глобальной привлекательности DFE является наличие следующей линейной системы с периодическими коэффициентами: ${\displaystyle \beta (t)}$

${\displaystyle {\begin{aligned}{\frac {dE_{1}}{dt}}&=\beta (t)I_{1}-(\gamma +a)E_{1}\\[8pt]{\frac {dI_{1}}{dt}}&=aE_{1}-(\gamma +\mu )I_{1}\end{aligned}}}$

устойчив (т. е. имеет собственные значения Флоке внутри единичного круга в комплексной плоскости).

Модель СЕИС

Модель SEIS аналогична модели SEIR (см. выше), за исключением того, что в конце не достигается иммунитет.

${\displaystyle {\color {blue}{{\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {S}}}}}$

В этой модели инфекция не оставляет никакого иммунитета, поэтому выздоровевшие люди снова становятся восприимчивыми и возвращаются в отсек S ( t ). Следующие дифференциальные уравнения описывают эту модель:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\Lambda -{\frac {\beta SI}{N}}-\mu S+\gamma I\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\epsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\end{aligned}}}$

Модель MSEIR

Для случая заболевания с факторами пассивного иммунитета и латентным периодом существует модель MSEIR.

${\displaystyle \color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}}}$

${\displaystyle {\begin{aligned}{\frac {dM}{dt}}&=\Lambda -\delta M-\mu M\\[6pt]{\frac {dS}{dt}}&=\delta M-{\frac {\beta SI}{N}}-\mu S\\[6pt]{\frac {dE}{dt}}&={\frac {\beta SI}{N}}-(\varepsilon +\mu )E\\[6pt]{\frac {dI}{dt}}&=\varepsilon E-(\gamma +\mu )I\\[6pt]{\frac {dR}{dt}}&=\gamma I-\mu R\end{aligned}}}$

Модель MSEIRS

Модель MSEIRS аналогична MSEIR, но иммунитет класса R будет временным, так что люди восстановят свою восприимчивость, когда временный иммунитет закончится.

${\displaystyle {\color {blue}{{\mathcal {M}}\to {\mathcal {S}}\to {\mathcal {E}}\to {\mathcal {I}}\to {\mathcal {R}}\to {\mathcal {S}}}}}$

Переменная частота контактов

Общеизвестно, что вероятность заболеть не постоянна во времени. По мере развития пандемии реакции на пандемию могут изменить уровень контактов, который в более простых моделях считается постоянным. Контрмеры, такие как маски, социальное дистанцирование и изоляция, изменят уровень контактов таким образом, чтобы снизить скорость пандемии.

Кроме того, некоторые заболевания носят сезонный характер, например, вирусы простуды , которые более распространены зимой. При детских заболеваниях, таких как корь, эпидемический паротит и краснуха, существует сильная корреляция со школьным календарем, так что во время школьных каникул вероятность заболеть таким заболеванием резко снижается. Как следствие, для многих классов заболеваний следует учитывать силу заражения с периодическим («сезонным») изменением скорости контакта.

${\displaystyle F=\beta (t){\frac {I}{N}},\quad \beta (t+T)=\beta (t)}$

с периодом Т, равным одному году.

Таким образом, наша модель становится

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta (t){\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta (t){\frac {I}{N}}S-(\gamma +\mu )I\end{aligned}}}$

(динамика восстанавливаемых легко следует из ), т.е. нелинейная система дифференциальных уравнений с периодически меняющимися параметрами. Хорошо известно, что в этом классе динамических систем могут наблюдаться очень интересные и сложные явления нелинейного параметрического резонанса. В этом легко убедиться, если: ${\displaystyle R=N-S-I}$

${\displaystyle {\frac {1}{T}}\int _{0}^{T}{\frac {\beta (t)}{\mu +\gamma }}\,dt<1\Rightarrow \lim _{t\to +\infty }(S(t),I(t))=DFE=(N,0),}$

тогда как если интеграл больше единицы, болезнь не вымрет и могут быть такие резонансы. Например, если рассматривать периодически меняющуюся частоту контактов как «вход» системы, то выходной сигнал представляет собой периодическую функцию, период которой кратен периоду входного сигнала. Это позволило внести вклад в объяснение многолетних (обычно двухгодичных) эпидемических вспышек некоторых инфекционных заболеваний как взаимодействия между периодом колебаний частоты контактов и псевдопериодом затухающих колебаний вблизи эндемического равновесия. Примечательно, что в некоторых случаях поведение также может быть квазипериодическим или даже хаотичным.

Модель SIR с диффузией

Пространственно-временные компартментальные модели описывают не общее количество, а плотность восприимчивых/инфицированных/выздоровевших лиц. Следовательно, они также позволяют моделировать распространение инфицированных в космосе. В большинстве случаев это делается путем объединения модели SIR с уравнением диффузии.

${\displaystyle {\begin{aligned}&\partial _{t}S=D_{S}\nabla ^{2}S-{\frac {\beta IS}{N}},\\[6pt]&\partial _{t}I=D_{I}\nabla ^{2}I+{\frac {\beta IS}{N}}-\gamma I,\\[6pt]&\partial _{t}R=D_{R}\nabla ^{2}R+\gamma I,\end{aligned}}}$^[33]

где , и – константы диффузии. Таким образом, получается уравнение реакции-диффузии. (Обратите внимание, что по причинам размерности этот параметр необходимо изменить по сравнению с простой моделью SIR.) Ранние модели этого типа использовались для моделирования распространения черной смерти в Европе. ^[34] Расширения этой модели использовались, например, для учета эффектов нефармацевтических вмешательств, таких как социальное дистанцирование. ^[35] ${\displaystyle D_{S}}$ ${\displaystyle D_{I}}$ ${\displaystyle D_{R}}$ ${\displaystyle \beta }$

Взаимодействующая модель субпопуляции SEIR

Поскольку социальные контакты, тяжесть заболевания и летальность, а также эффективность профилактических мер могут существенно различаться между взаимодействующими субпопуляциями, например, пожилыми и молодыми, для каждой подгруппы могут использоваться отдельные модели SEIR, связанные между собой связями взаимодействия. ^[33] Такие модели взаимодействующих субпопуляций SEIR использовались для моделирования пандемии COVID-19 в масштабах континента для разработки персонализированных, ускоренных, ориентированных на субпопуляции стратегий вакцинации ^[36] , которые обещают сокращение пандемии и снижение количества случаев заболевания и смертности. в условиях ограниченного доступа к вакцинам во время волны вирусных вариантов, вызывающих обеспокоенность.

Модель SIR в сетях

Модель SIR изучалась на сетях различных типов, чтобы смоделировать более реалистичную форму соединения, чем обычно требуемое условие однородного смешивания. Простая модель эпидемий в сетях, в которой человек имеет вероятность p заразиться от каждого из своих инфицированных соседей за заданный временной шаг, приводит к результатам, аналогичным формированию гигантских компонентов на случайных графах Эрдеша Реньи . ^[37]

Модель SIR SS – сочетание SIR с моделированием социального стресса.

Динамика эпидемий зависит от того, как меняется поведение людей во времени. Например, в начале эпидемии люди невежественны и беспечны, затем, после начала эпидемий и тревоги, они начинают соблюдать различные ограничения и распространение эпидемий может пойти на спад. Со временем некоторые люди устают/разочаровываются в ограничениях и перестают им следовать (утомление), особенно если количество новых случаев падает. Отдохнув некоторое время, они могут снова соблюдать ограничения. Но во время этой паузы может прийти вторая волна и стать даже сильнее первой. Необходимо учитывать социальную динамику . Социально -физические модели социального стресса дополняют классические модели эпидемий. ^[38]

Показан пример использования числовой модели SIR для соответствия данным о COVID-19 (из Центра по контролю и профилактике заболеваний США) в штате Огайо, США, подобранным с использованием модели SIR и SIRV. Обратите внимание: хотя модель SIR может моделировать отдельную волну, более сложная модель, такая как SIR _SS, лучше моделирует несколько волн. ^{[21] [22]} ${\displaystyle R_{t}}$

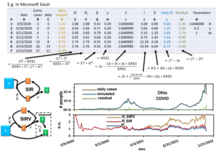
Простейшая модель SIR-социального стресса (SIR _SS ) устроена следующим образом. Восприимчивых лиц (S) можно разделить на три подгруппы по типам поведения: неосведомленные или не подозревающие об эпидемии (S _ign ), рационально устойчивые (S _res ) и истощенные (S _exh ), не реагирующие на внешние раздражители. (это своего рода рефрактерный период). Другими словами: S(t) = S _ign (t) + S _res (t) + S _exh (t). Условно модель социального стресса можно представить в виде «схемы реакции» (где I обозначает инфицированных):

• ${\displaystyle {\color {blue}{{\mathcal {S_{ign}}}+2{\mathcal {I}}\to {\mathcal {S_{res}}}+2{\mathcal {I}}}}}$– реакция мобилизации (автокаталитическая форма здесь означает, что скорость перехода пропорциональна квадрату инфицированной фракции I);
• ${\displaystyle {\color {blue}{{\mathcal {S_{res}}}\to {\mathcal {S_{exh}}}}}}$– процесс истощения вследствие утомления от противоэпидемических ограничений;
• ${\displaystyle {\color {blue}{{\mathcal {S_{exh}}}\to {\mathcal {S_{ign}}}}}}$– медленная релаксация до исходного состояния (конец рефрактерного периода).

Основная эпидемическая реакция СИР

• ${\displaystyle {\color {blue}{{\mathcal {S_{...}}}+{\mathcal {I}}\to {\mathcal {2I}}}}}$

имеет разные константы скорости реакции для _Sign , S _res и S _exh . Предположительно, для Sres _ниже , чем для _Sign и _Sign . ${\displaystyle \beta }$ ${\displaystyle \beta }$

Различия между странами сосредоточены в двух кинетических константах: скорости мобилизации и скорости истощения, рассчитанной для эпидемии COVID-19 в 13 странах. ^[38] Эти константы для этой эпидемии во всех странах можно получить путем подбора модели SIR _SS к общедоступным данным ^[39]

Уравнение КдВ-СИР

На основе классической модели SIR предложено уравнение Кортевега-де Фриза (КдВ)-SIR и его аналитическое решение, иллюстрирующие фундаментальную динамику эпидемической волны, зависимость решений от параметров и зависимость горизонтов прогнозируемости от различных факторов. виды решений. ^[40] Уравнение КдВ-СИР записывается следующим образом:

${\displaystyle {\frac {d^{2}I}{dt}}-\sigma _{o}^{2}I+{\frac {3}{2}}{\frac {\sigma _{o}^{2}}{I_{max}}}I^{2}=0}$.

Здесь,

${\displaystyle \sigma _{o}=\gamma (R_{o}-1)}$,

${\displaystyle R_{o}={\frac {\beta }{\gamma }}{\frac {S_{o}}{N}}}$,

и

${\displaystyle I_{max}={\frac {S_{o}}{2}}{\frac {(R_{o}-1)^{2}}{R_{o}^{2}}}}$.

${\displaystyle S_{o}}$указывает начальное значение переменной состояния . Параметры (σ-ноль) и (R-ноль) представляют собой не зависящую от времени относительную скорость роста и базовое число воспроизводства соответственно. представляет максимум переменных состояния (по количеству инфицированных). Аналитическое решение уравнения КдВ-СИР записывается следующим образом: ${\displaystyle S}$ ${\displaystyle \sigma _{o}}$ ${\displaystyle R_{o}}$ ${\displaystyle I_{max}}$ ${\displaystyle I}$

${\displaystyle I=I_{max}sech^{2}\left({\frac {\sigma _{o}}{2}}t\right)}$,

которое представляет собой уединенное волновое решение.

Моделирование вакцинации

Модель SIR можно модифицировать для моделирования вакцинации. ^[41] Обычно они вводят дополнительный отсек в модель SIR для вакцинированных лиц. Ниже приведены некоторые примеры. ${\displaystyle V}$

Вакцинация новорожденных

При наличии инфекционного заболевания одной из основных задач является его ликвидация с помощью профилактических мер и, по возможности, внедрения программы массовой вакцинации. Рассмотрим заболевание, от которого новорожденного прививают (вакциной, дающей пожизненный иммунитет) в размере : ${\displaystyle P\in (0,1)}$

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\nu N(1-P)-\mu S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dI}{dt}}&=\beta {\frac {I}{N}}S-(\mu +\gamma )I\\[8pt]{\frac {dV}{dt}}&=\nu NP-\mu V\end{aligned}}}$

где класс вакцинированных субъектов. Сразу видно, что: ${\displaystyle V}$

${\displaystyle \lim _{t\to +\infty }V(t)=NP,}$

таким образом, мы будем иметь дело с долгосрочным поведением и , для которого справедливо следующее: ${\displaystyle S}$ ${\displaystyle I}$

${\displaystyle R_{0}(1-P)\leq 1\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=DFE=\left(N\left(1-P\right),0\right)}$

${\displaystyle R_{0}(1-P)>1,\quad I(0)>0\Rightarrow \lim _{t\to +\infty }\left(S(t),I(t)\right)=EE=\left({\frac {N}{R_{0}(1-P)}},N\left(R_{0}(1-P)-1\right)\right).}$

Другими словами, если

${\displaystyle P<P^{*}=1-{\frac {1}{R_{0}}}}$

программа вакцинации не сможет искоренить болезнь, наоборот, она останется эндемической, хотя и на более низком уровне, чем в случае отсутствия прививок. Это означает, что математическая модель предполагает, что для болезни, базовое репродуктивное число которой может достигать 18, необходимо вакцинировать не менее 94,4% новорожденных, чтобы искоренить болезнь.

Вакцинация и информация

Современное общество сталкивается с проблемой «рационального» освобождения, то есть решения семьи не вакцинировать детей вследствие «рационального» сравнения предполагаемого риска заражения и риска получения ущерба от вакцины. Чтобы оценить, действительно ли такое поведение рационально, т. е. может ли оно в равной степени привести к искоренению болезни, можно просто предположить, что уровень вакцинации является возрастающей функцией числа заразившихся:

${\displaystyle P=P(I),\quad P'(I)>0.}$

В таком случае условием эрадикации становится:

${\displaystyle P(0)\geq P^{*},}$

т.е. базовый уровень вакцинации должен превышать порог «обязательной вакцинации», который в случае исключения не может соблюдаться. Таким образом, «рациональное» исключение может быть близоруким, поскольку оно основано только на нынешнем низком уровне заболеваемости из-за высокого охвата прививками, а не на учете будущего возобновления инфекции из-за снижения охвата.

Вакцинация неноворожденных

В случае, если также проводятся вакцинации неноворожденных с частотой ρ, уравнение для восприимчивого и вакцинированного субъекта должно быть изменено следующим образом:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N(1-P)-\mu S-\rho S-\beta {\frac {I}{N}}S\\[8pt]{\frac {dV}{dt}}&=\mu NP+\rho S-\mu V\end{aligned}}}$

что приводит к следующему состоянию эрадикации:

${\displaystyle P\geq 1-\left(1+{\frac {\rho }{\mu }}\right){\frac {1}{R_{0}}}}$

Стратегия импульсной вакцинации

В рамках этой стратегии с течением времени проводится повторная вакцинация определенной возрастной группы (например, маленьких детей или пожилых людей) в восприимчивом населении. Используя эту стратегию, блок восприимчивых людей немедленно удаляется, что позволяет исключить инфекционное заболевание (например, корь) среди всего населения. Каждые единицы времени T вакцинируют постоянную долю p восприимчивых субъектов за относительно короткое (по отношению к динамике заболевания) время. Это приводит к следующим импульсным дифференциальным уравнениям для восприимчивых и вакцинированных субъектов:

${\displaystyle {\begin{aligned}{\frac {dS}{dt}}&=\mu N-\mu S-\beta {\frac {I}{N}}S,\quad S(nT^{+})=(1-p)S(nT^{-}),&&n=0,1,2,\ldots \\[8pt]{\frac {dV}{dt}}&=-\mu V,\quad V(nT^{+})=V(nT^{-})+pS(nT^{-}),&&n=0,1,2,\ldots \end{aligned}}}$

Легко видеть, что, установив I = 0, можно получить, что динамика восприимчивых субъектов определяется следующим образом:

${\displaystyle S^{*}(t)=1-{\frac {p}{1-(1-p)E^{-\mu T}}}E^{-\mu MOD(t,T)}}$

и что условием эрадикации является:

${\displaystyle R_{0}\int _{0}^{T}S^{*}(t)\,dt<1}$

Влияние возраста: возрастные модели

Возраст оказывает глубокое влияние на скорость распространения заболевания среди населения, особенно на частоту контактов. Этот показатель суммирует эффективность контактов между восприимчивыми и заразными субъектами. Учитывая возраст эпидемических классов (ограничимся схемой «восприимчивый-инфекционный-удаленный»), такой, что: ${\displaystyle s(t,a),i(t,a),r(t,a)}$

${\displaystyle S(t)=\int _{0}^{a_{M}}s(t,a)\,da}$

${\displaystyle I(t)=\int _{0}^{a_{M}}i(t,a)\,da}$

${\displaystyle R(t)=\int _{0}^{a_{M}}r(t,a)\,da}$

(где – максимально допустимый возраст) и их динамика описывается не «простыми» уравнениями в частных производных, а интегро-дифференциальными уравнениями : ${\displaystyle a_{M}\leq +\infty }$

${\displaystyle \partial _{t}s(t,a)+\partial _{a}s(t,a)=-\mu (a)s(a,t)-s(a,t)\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

${\displaystyle \partial _{t}i(t,a)+\partial _{a}i(t,a)=s(a,t)\int _{0}^{a_{M}}{k(a,a_{1};t)i(a_{1},t)da_{1}}-\mu (a)i(a,t)-\gamma (a)i(a,t)}$

${\displaystyle \partial _{t}r(t,a)+\partial _{a}r(t,a)=-\mu (a)r(a,t)+\gamma (a)i(a,t)}$

где:

${\displaystyle F(a,t,i(\cdot ,\cdot ))=\int _{0}^{a_{M}}k(a,a_{1};t)i(a_{1},t)\,da_{1}}$

- это сила заражения, которая, конечно, будет зависеть, хотя и контактного ядра, от взаимодействия эпох. ${\displaystyle k(a,a_{1};t)}$

Сложности добавляют начальные условия для новорожденных (т.е. для a=0), которые прямо заразны и удалены:

${\displaystyle i(t,0)=r(t,0)=0}$

но они нелокальны для плотности восприимчивых новорожденных:

${\displaystyle s(t,0)=\int _{0}^{a_{M}}\left(\varphi _{s}(a)s(a,t)+\varphi _{i}(a)i(a,t)+\varphi _{r}(a)r(a,t)\right)\,da}$

где фертильность взрослых. ${\displaystyle \varphi _{j}(a),j=s,i,r}$

Более того, определив теперь плотность всего населения, получим: ${\displaystyle n(t,a)=s(t,a)+i(t,a)+r(t,a)}$

${\displaystyle \partial _{t}n(t,a)+\partial _{a}n(t,a)=-\mu (a)n(a,t)}$

В простейшем случае равенства рождаемости в трех эпидемических классах мы имеем, что для демографического равновесия должно выполняться следующее необходимое и достаточное условие, связывающее рождаемость со смертностью : ${\displaystyle \varphi (.)}$ ${\displaystyle \mu (a)}$

${\displaystyle 1=\int _{0}^{a_{M}}\varphi (a)\exp \left(-\int _{0}^{a}{\mu (q)dq}\right)\,da}$

и демографическое равновесие

${\displaystyle n^{*}(a)=C\exp \left(-\int _{0}^{a}\mu (q)\,dq\right),}$

автоматически гарантируя существование безболезненного решения:

${\displaystyle DFS(a)=(n^{*}(a),0,0).}$

Базовое число воспроизводства можно рассчитать как спектральный радиус соответствующего функционального оператора.

Метод нового поколения

Один из способов расчета — усреднить ожидаемое количество новых заражений по всем возможным типам зараженных. Метод следующего поколения — это общий метод определения, когда задействовано более одного класса инфекционных заболеваний. Этот метод, первоначально предложенный Diekmann et al . (1990), ^[42] могут использоваться для моделей, в основе которых лежит возрастная структура или пространственная структура, среди других возможностей. ^[43] На этом изображении спектральный радиус матрицы следующего поколения дает базовое число воспроизведений, ^[44] ${\displaystyle R_{0}}$ ${\displaystyle R_{0}}$ ${\displaystyle G}$ ${\displaystyle R_{0}=\rho (G).}$

Рассмотрим заболевание, передающееся половым путем. В наивной популяции, где почти все восприимчивы, но семя инфекции, если ожидаемое число представителей пола 1 равно , а ожидаемое число инфицированных пола 2 равно , мы можем знать, сколько людей будет инфицировано в следующем поколении. Так что матрицу следующего поколения можно записать как: ^[45] ${\displaystyle f}$ ${\displaystyle m}$ ${\displaystyle G}$

$${\displaystyle G={\begin{pmatrix}0&f\\m&0\end{pmatrix}},}$$

${\displaystyle g_{ij}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle i}$ ${\displaystyle f}$ ${\displaystyle m}$ ${\displaystyle g_{ij}}$ ${\displaystyle a}$ ${\displaystyle \phi _{a}}$ ${\displaystyle \phi _{a+1}}$ ${\displaystyle G\phi _{a}}$

Спектральный радиус матрицы следующего поколения — это базовое число воспроизводства, то есть здесь среднее геометрическое ожидаемого числа представителей каждого пола в следующем поколении. Обратите внимание, что коэффициенты умножения и чередуются, поскольку заразный человек должен «пройти через» второй пол, прежде чем он сможет войти в нового хозяина первого пола. Другими словами, чтобы вернуться к одному и тому же типу, требуется два поколения, и числа каждых двух поколений умножаются на × . Таким образом, средний коэффициент умножения на поколение составляет . Обратите внимание, что это неотрицательная матрица, поэтому она имеет единственное, уникальное, положительное, действительное собственное значение, которое строго больше, чем все остальные. ${\displaystyle R_{0}=\rho (G)={\sqrt {mf}}}$ ${\displaystyle f}$ ${\displaystyle m}$ ${\displaystyle m}$ ${\displaystyle f}$ ${\displaystyle {\sqrt {mf}}}$ ${\displaystyle G}$

Матрица нового поколения для секционных моделей

При математическом моделировании инфекционных заболеваний динамика распространения обычно описывается с помощью системы нелинейных обыкновенных дифференциальных уравнений (ОДУ). Таким образом, всегда существуют связанные уравнения формы , которые показывают, как количество людей в отсеке меняется с течением времени. Например, в модели SIR , , и . Компартментальные модели имеют равновесие без болезней (DFE), что означает, что можно найти равновесие, установив количество инфицированных людей равным нулю . Другими словами, как правило, существует безинфекционное устойчивое состояние . Это решение также обычно гарантирует, что равновесие без болезней также является равновесием системы. Существует еще одна фиксированная точка , известная как эндемическое равновесие (ЭР), когда болезнь не полностью искоренена и остается в популяции. Математически это порог устойчивости безболезненного равновесия, такой, что: ${\displaystyle n}$ ${\displaystyle {\dot {C_{i}}}={\operatorname {d} \!C_{i} \over \operatorname {d} \!t}=f(C_{1},C_{2},...,C_{n})}$ ${\displaystyle C_{i}}$ ${\displaystyle C_{1}=S}$ ${\displaystyle C_{2}=I}$ ${\displaystyle C_{3}=R}$ ${\displaystyle I=0}$ ${\displaystyle R_{0}}$

${\displaystyle R_{0}\leq 1\Rightarrow \lim _{t\to \infty }(C_{1}(t),C_{2}(t),\cdots ,C_{n}(t))={\textrm {DFE}}}$

${\displaystyle R_{0}>1,I(0)>0\Rightarrow \lim _{t\to \infty }(C_{1}(t),C_{2}(t),\cdots ,C_{n}(t))={\textrm {EE}}.}$

Чтобы вычислить , первым шагом является линеаризация вокруг безболезненного равновесия (DFE), но для инфицированной подсистемы нелинейных ODE, которые описывают возникновение новых инфекций и изменения состояния среди инфицированных людей. С эпидемиологической точки зрения линеаризация отражает то, что характеризует потенциал первоначального распространения заразного человека среди наивного населения, при условии, что изменение в восприимчивой популяции незначительно во время первоначального распространения. ^[46] Линейную систему ОДУ всегда можно описать матрицей. Итак, следующим шагом будет построение линейного положительного оператора, который обеспечит следующее поколение инфицированных людей при применении к нынешнему поколению. Обратите внимание, что этот оператор (матрица) отвечает за количество зараженных, а не за все отсеки. Итерация этого оператора описывает начальное развитие инфекции в гетерогенной популяции. Так что сравнение спектрального радиуса этого оператора с единицей определяет, будут ли расти поколения зараженных людей или нет. может быть записана как произведение уровня инфицирования вблизи безболезненного равновесия и средней продолжительности заразности. Он используется для определения пика и окончательного размера эпидемии. ${\displaystyle R_{0}}$ ${\displaystyle R_{0}}$ ${\displaystyle R_{0}}$

Модель SEIR с динамикой естественного движения населения и постоянной численностью населения.

Как описано в приведенном выше примере, очень многие эпидемические процессы можно описать с помощью модели SIR‌. Однако для многих важных инфекций, таких как COVID-19 , существует значительный латентный период, в течение которого люди инфицированы, но сами еще не заразны. В этот период человек находится в отсеке Е (для облученных). Здесь формирование матрицы следующего поколения из модели SEIR‌ включает определение двух компартментов: инфицированного и неинфицированного, поскольку они являются популяциями, которые распространяют инфекцию. Таким образом, нам нужно смоделировать только незащищенные E и зараженные I отсеки. Рассмотрим популяцию, характеризующуюся уровнем смертности и рождаемости , в которой распространяется инфекционное заболевание. Как и в предыдущем примере, мы можем использовать коэффициенты перехода между компартментами на душу населения, такие как уровень заражения, уровень выздоровления и уровень, с которым латентный человек становится заразным. Затем мы можем определить динамику модели, используя следующие уравнения: ^{[43] [47]} ${\displaystyle \mu }$ ${\displaystyle \lambda }$ ${\displaystyle \beta }$ ${\displaystyle \gamma }$ ${\displaystyle \kappa }$

$${\displaystyle {\begin{cases}{\dot {S}}=\lambda -\mu S-\beta SI,\\\\{\dot {E}}=\beta SI-(\mu +\kappa )E,\\\\{\dot {I}}=\kappa E-(\mu +\gamma )I,\\\\{\dot {R}}=\gamma I-\mu R.\end{cases}}}$$

${\displaystyle \mathrm {x} =(S,E,I,R)}$ ${\displaystyle \mathrm {x} _{i}}$ ${\displaystyle i}$ ${\displaystyle F_{i}(\mathrm {x} )}$ ${\displaystyle i}$ ${\displaystyle V_{i}^{+}}$ ${\displaystyle i}$ ${\displaystyle V_{i}^{-}}$ ${\displaystyle i}$ ${\displaystyle F_{i}(\mathrm {x} )-V_{i}(\mathrm {x} )}$ ${\displaystyle V_{i}(\mathrm {x} )=V_{i}^{-}(\mathrm {x} )-V_{i}^{+}(\mathrm {x} )}$

Теперь мы можем составить матрицы частных производных от и такие, что ${\displaystyle F}$ ${\displaystyle V}$

${\displaystyle F_{ij}={\partial \!\ F_{i}(\mathrm {x} ^{*}) \over \partial \!\ \mathrm {x} _{j}}}$и , где – безболезненное равновесие. ${\displaystyle V_{ij}={\partial \!\ V_{i}(\mathrm {x} ^{*}) \over \partial \!\ \mathrm {x} _{j}}}$ ${\displaystyle \mathrm {x} ^{*}=(S^{*},E^{*},I^{*},R^{*})=(\lambda /\mu ,0,0,0)}$

Теперь мы можем сформировать матрицу (оператор) следующего поколения . ^{[48] ​​[44]} По сути, это неотрицательная матрица , которая представляет уровни заражения вблизи равновесия, и представляет собой M-матрицу для линейных переходных условий, образующую матрицу, которая представляет среднюю продолжительность заразности. Таким образом, он показывает скорость, с которой инфицированные люди вызывают новые инфекции , в разах средней продолжительности времени, которое человек проводит за одно посещение отсека. ${\displaystyle G=FV^{-1}}$ ${\displaystyle F}$ ${\displaystyle V}$ ${\displaystyle V^{-1}}$ ${\displaystyle G_{ij}}$ ${\displaystyle \mathrm {x} _{j}}$ ${\displaystyle \mathrm {x} _{i}}$ ${\displaystyle j.}$

Наконец, для этого процесса SEIR мы можем иметь:

${\displaystyle F={\begin{pmatrix}0&\beta S^{*}\\0&0\end{pmatrix}}}$и и так ${\displaystyle V={\begin{pmatrix}\mu +\kappa &0\\-\kappa &\gamma +\mu \end{pmatrix}}}$ ${\displaystyle R_{0}=\rho (FV^{-1})={\frac {\kappa \beta S^{*}}{(\mu +\kappa )(\mu +\gamma )}}.}$

Методы оценки

Базовое репродуктивное число можно оценить путем изучения подробных цепочек передачи или с помощью геномного секвенирования . Однако чаще всего его рассчитывают с использованием эпидемиологических моделей. ^[49] Во время эпидемии обычно известно количество диагностированных инфекций с течением времени . На ранних стадиях эпидемии рост носит экспоненциальный характер, с логарифмическими темпами роста. ${\displaystyle N(t)}$ ${\displaystyle t}$

$${\displaystyle K:={\frac {d\ln(N)}{dt}}.}$$

${\displaystyle N}$ ${\displaystyle R_{0}}$

При экспоненциальном росте это связано со временем удвоения как ${\displaystyle K}$ ${\displaystyle T_{d}}$

$${\displaystyle K={\frac {\ln(2)}{T_{d}}}.}$$

Простая модель

Если особь после заражения заражает ровно новых особей только по прошествии ровно времени (серийного интервала), то число заразных особей с течением времени растет как ${\displaystyle R_{0}}$ ${\displaystyle \tau }$

$${\displaystyle n_{E}(t)=n_{E}(0)\,R_{0}^{t/\tau }=n_{E}(0)\,e^{Kt}}$$

$${\displaystyle \ln(n_{E}(t))=\ln(n_{E}(0))+\ln(R_{0})t/\tau .}$$

$${\displaystyle {\frac {dn_{E}(t)}{dt}}=n_{E}(t){\frac {\ln(R_{0})}{\tau }}.}$$

$${\displaystyle {\frac {d\ln(n_{E}(t))}{dt}}={\frac {\ln(R_{0})}{\tau }}.}$$

${\displaystyle R_{0}=e^{K\tau }}$ ${\displaystyle K={\frac {\ln R_{0}}{\tau }}}$

Например, с помощью и мы найдем . ${\displaystyle \tau =5~\mathrm {d} }$ ${\displaystyle K=0.183~\mathrm {d} ^{-1}}$ ${\displaystyle R_{0}=2.5}$

Если зависит от времени ${\displaystyle R_{0}}$

$${\displaystyle \ln(n_{E}(t))=\ln(n_{E}(0))+{\frac {1}{\tau }}\int \limits _{0}^{t}\ln(R_{0}(t))dt}$$

${\displaystyle \ln(R_{0})}$

Латентный инфекционный период, изоляция после установления диагноза.

В этой модели индивидуальное заражение имеет следующие стадии:

1. Зараженный: человек инфицирован, но не имеет симптомов и еще не заражает других. Средняя продолжительность экспонированного состояния составляет . ${\displaystyle \tau _{E}}$
2. Латентная инфекция: человек инфицирован, не имеет симптомов, но заражает других. Средняя продолжительность латентного инфекционного состояния составляет . В этот период особь заражает других особей. ${\displaystyle \tau _{I}}$ ${\displaystyle R_{0}}$
3. Изоляция после постановки диагноза: принимаются меры для предотвращения дальнейшего заражения, например, путем изоляции инфицированного человека.

Это модель SEIR, которую можно записать в следующем виде ^[50] ${\displaystyle R_{0}}$

$${\displaystyle R_{0}=1+K(\tau _{E}+\tau _{I})+K^{2}\tau _{E}\tau _{I}.}$$

COVID-19SARS ${\displaystyle n_{E}}$ ${\displaystyle n_{I}}$

$${\displaystyle {\frac {d}{dt}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}={\begin{pmatrix}-1/\tau _{E}&R_{0}/\tau _{I}\\1/\tau _{E}&-1/\tau _{I}\end{pmatrix}}{\begin{pmatrix}n_{E}\\n_{I}\end{pmatrix}}.}$$

собственное значение ${\displaystyle K}$ ${\displaystyle R_{0}}$

В частном случае эта модель дает результат , который отличается от простой модели, приведенной выше ( ). Например, при тех же значениях и мы найдем вместо истинного значения . Разница обусловлена ​​тонким различием в базовой модели роста; приведенное выше матричное уравнение предполагает, что вновь инфицированные пациенты в настоящее время уже способствуют инфекциям, тогда как на самом деле инфекции происходят только из-за числа инфицированных ранее . Более корректная трактовка потребовала бы использования дифференциальных уравнений с запаздыванием . ^[51] ${\displaystyle \tau _{I}=0}$ ${\displaystyle R_{0}=1+K\tau _{E}}$ ${\displaystyle R_{0}=\exp(K\tau _{E})}$ ${\displaystyle \tau =5~\mathrm {d} }$ ${\displaystyle K=0.183~\mathrm {d} ^{-1}}$ ${\displaystyle R_{0}=1.9}$ ${\displaystyle 2.5}$ ${\displaystyle \tau _{E}}$

Латентный период – это переходный период между событием заражения и проявлением заболевания. При заболеваниях с различным латентным периодом базовое число воспроизводства можно рассчитать как сумму чисел воспроизводства за каждый период перехода в заболевание. Примером этого является туберкулез (ТБ). Блоуэр и соавторы на основе простой модели туберкулеза рассчитали следующее число воспроизводства: ^[52]

$${\displaystyle R_{0}=R_{0}^{\text{FAST}}+R_{0}^{\text{SLOW}}}$$

^[53]

Другие соображения в рамках компартментальных моделей эпидемии

Вертикальная передача

В случае некоторых заболеваний, таких как СПИД и гепатит В, дети инфицированных родителей могут родиться инфицированными. Такая передача заболевания вниз от матери называется вертикальной передачей. Приток дополнительных членов в зараженную категорию можно учитывать в рамках модели, включая часть новорожденных членов в зараженный отсек. ^[54]

Векторная передача

Болезни, передающиеся от человека к человеку косвенно, т.е. малярия, распространяющаяся через комаров, передаются через переносчиков. В этих случаях инфекция передается от человека к насекомому, и модель эпидемии должна включать оба вида, что обычно требует гораздо большего количества компартментов, чем модель прямой передачи. ^{[54] [55]}

Другие

К другим событиям, которые, возможно, придется учитывать при моделировании эпидемии, относятся следующие: ^[54]

• Неоднородное смешивание
• Переменная инфекционность
• Распределения, которые пространственно неоднородны
• Заболевания, вызываемые макропаразитами

Детерминистические и стохастические модели эпидемии

Важно подчеркнуть, что представленные здесь детерминистические модели действительны только в случае достаточно больших популяций, и поэтому их следует использовать с осторожностью. ^{[56] [57]}

Точнее, эти модели действительны только в термодинамическом пределе , когда популяция фактически бесконечна. В стохастических моделях долговременное эндемическое равновесие, полученное выше, не соблюдается, поскольку существует конечная вероятность того, что количество инфицированных людей в системе упадет ниже одного. Таким образом, в настоящей системе патоген не может распространяться, поскольку ни один хозяин не будет инфицирован. Но в детерминированных моделях среднего поля количество зараженных может принимать реальные, а именно нецелые значения зараженных хостов, а количество хостов в модели может быть меньше единицы, но больше нуля, что позволяет патоген в модели для распространения. Надежность отсекаемых моделей ограничена отсеками.

Одно из возможных расширений моделей среднего поля рассматривает распространение эпидемий по сети на основе концепций теории просачивания . ^[37] Стохастические эпидемические модели изучались в различных сетях ^{[58] [59] [60]} и совсем недавно были применены к пандемии COVID-19 . ^[61]

Смотрите также

• Скорость атаки
• Базовый номер репродукции
• Сгладить кривую
• Список имитационных моделей COVID-19
• Математическое моделирование в эпидемиологии
• Проблема с модифицируемой единицей площади
• Матрица нового поколения
• Оценка риска

Рекомендации

1. Росс Р. (1 февраля 1916 г.). «Применение теории вероятностей к изучению априорной патометрии. Часть I». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 92 (638): 204–230. Бибкод : 1916RSPSA..92..204R. дои : 10.1098/rspa.1916.0007 .
2. Росс Р., Хадсон Х (3 мая 1917 г.). «Применение теории вероятностей к изучению априорной патометрии. Часть II». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 93 (650): 212–225. Бибкод : 1917RSPSA..93..212R. дои : 10.1098/rspa.1917.0014 .
3. Росс Р., Хадсон Х (1917). «Применение теории вероятностей к изучению априорной патометрии. Часть III». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 89 (621): 225–240. Бибкод : 1917RSPSA..93..225R. дои : 10.1098/rspa.1917.0015 .
4. Кермак В.О., Маккендрик АГ (1927). «Вклад в математическую теорию эпидемий». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера . 115 (772): 700–721. Бибкод : 1927RSPSA.115..700K. дои : 10.1098/rspa.1927.0118 .
5. Кендалл Д.Г. (1956). «Детерминистические и стохастические эпидемии в закрытых группах населения». Вклад в биологию и проблемы здравоохранения . Том. 4. Издательство Калифорнийского университета. стр. 149–165. дои : 10.1525/9780520350717-011. ISBN 978-0-520-35071-7. МР  0084936. Збл  0070.15101.
6. Энгельманн, Лукас (30 августа 2021 г.). «Коробка, корыто и шарики: как теория эпидемии Рида-Фроста сформировала эпидемиологические рассуждения в 20 веке». История и философия наук о жизни . 43 (3): 105. doi :10.1007/s40656-021-00445-z. ISSN  1742-6316. ПМЦ 8404547 . ПМИД  34462807. 
7. Харко Т, Лобо Ф.С., Мак МК (2014). «Точные аналитические решения модели эпидемии восприимчивых-инфицированных-выздоровевших (SIR) и модели SIR с равными уровнями смертности и рождаемости». Прикладная математика и вычислительная техника . 236 : 184–194. arXiv : 1403.2160 . Бибкод : 2014arXiv1403.2160H. дои : 10.1016/j.amc.2014.03.030. S2CID  14509477.
8. Бекли Р., Уэзерспун С., Александр М., Чендлер М., Джонсон А., Бхатт Г.С. (2013). «Моделирование эпидемий с помощью дифференциальных уравнений» (PDF) . Внутренний отчет Университета штата Теннесси . Проверено 19 июля 2020 г.
9. Крёгер М., Шликайзер Р. (2020). «Аналитическое решение SIR-модели временной эволюции эпидемий. Часть A: Независимый от времени коэффициент воспроизводства». Журнал физики А. 53 (50): 505601. Бибкод : 2020JPhA...53X5601K. дои : 10.1088/1751-8121/abc65d . S2CID  225555567.
10. Шликайзер Р., Крёгер М. (2021). «Аналитическое решение SIR-модели временной эволюции эпидемий. Часть B: Полувременной случай». Журнал физики А. 54 (17): 175601. Бибкод : 2021JPhA...54q5601S. дои : 10.1088/1751-8121/abed66 . hdl : 20.500.11850/479548 .
11. Ян В., Чжан Д., Пэн Л., Чжугэ С., Хун Л. (2020). «Рациональная оценка различных моделей эпидемии на основе данных о COVID-19 в Китае». arXiv : 2003.05666v1 [q-bio.PE].
12. Саймон, Кори (2020). «Динамическая модель передачи инфекционных заболеваний SIR и ее аналогия с химической кинетикой». PeerJ Физическая химия . 2 (2): е14. дои : 10.7717/peerj-pchem.14 .
13. Крылова О., Earn DJ (июль 2013 г.). «Влияние распределения инфекционного периода на прогнозируемые изменения в динамике детских заболеваний». Журнал Королевского общества, Интерфейс . 10 (84): 20130098. doi : 10.1098/rsif.2013.0098 . ПМЦ 3673147 . ПМИД  23676892. 
14. Хеткот Х (2000). «Математика инфекционных болезней». Обзор СИАМ . 42 (4): 599–653. Бибкод : 2000SIAMR..42..599H. дои : 10.1137/s0036144500371907. S2CID  10836889.
15. Бэйли, Норман Т.Дж. (1975). Математическая теория инфекционных болезней и ее приложения (2-е изд.). Лондон: Гриффин. ISBN 0-85264-231-8.
16. Соня Альтизер; Нанн, Чарльз (2006). Инфекционные болезни приматов: поведение, экология и эволюция . Оксфордская серия по экологии и эволюции. Оксфорд [Оксфордшир]: Издательство Оксфордского университета. ISBN 0-19-856585-2.
17. Wolfram Research, Inc. «Математика, версия 12.1». Шампейн, Иллинойс, 2020.
18. Капассо V (1993). Математическая структура эпидемических систем . Берлин: Шпрингер. ISBN 3-540-56526-4.
19. Миллер JC (сентябрь 2012 г.). «Заметка о выводе окончательных размеров эпидемии». Бюллетень математической биологии . 74 (9): 2125–2141. дои : 10.1007/s11538-012-9749-6. ПМК 3506030 . PMID  22829179. Раздел 4.1. 
20. Миллер Дж.К. (февраль 2017 г.). «Математические модели распространения заболевания SIR с комбинированным несексуальным и половым путем передачи». Моделирование инфекционных заболеваний . 2 (1): 35–55. дои : 10.1016/j.idm.2016.12.003. ПМЦ 5963332 . PMID  29928728. Раздел 2.1.3. 
21. Харт К.Д., Томпсон С., Бургер С., Хардвик Д., Мишо А.Х., Булуши А., Прайдмор С., Уорд С., Чен Дж. (2021). «Дистанционное обучение кинетическому анализу COVID-19 в лабораторном классе физической химии». АСУ Омега . 6 (43): 29223–29232. doi : 10.1021/acsomega.1c04842. ПМЦ 8547164 . ПМИД  34723043. 
22. Смит Д.К., Лауро К., Келли Д., Фиш Дж., Линтелман Э., МакИвен Д., Смит С., Стец М., Амбагаспития Т.Д., Чен Дж. (2022). «Преподавание физической химии в бакалавриате с использованием кинетического анализа COVID-19 в США». Журнал химического образования . 99 (10): 3471–3477. Бибкод : 2022JChEd..99.3471S. doi : 10.1021/acs.jchemed.2c00416. ПМЦ 9799982 . PMID  36589277. S2CID  251484056. 
23. Падуя RN, Туланг AB (2 декабря 2010 г.). «Эпидемиологическая модель распространения инфекционных заболеваний, зависящая от плотности». Liceo Журнал исследований высшего образования . 6 (2). дои : 10.7828/ljher.v6i2.62.
24. Мэй RM , Андерсон Б (24 сентября 1992 г.). Инфекционные болезни человека: динамика и контроль (пересмотренная ред.). Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-854040-3.
25. фон Чефалвай, Крис (01 января 2023 г.), фон Чефалвай, Крис (редактор), «Факторы хозяина», Вычислительное моделирование инфекционных заболеваний , Academic Press, стр. 93–119, doi : 10.1016/b978-0- 32-395389-4.00012-8 , ISBN 978-0-323-95389-4
26. Hethcote HW (1989). «Три основные эпидемиологические модели». В: Левин С.А., Халлам Т.Г., Гросс Л.Дж. (ред.). Прикладная математическая экология . Биоматематика. Том. 18. Берлин: Шпрингер. стр. 119–144. дои : 10.1007/978-3-642-61317-3_5. ISBN 3-540-19465-7.
27. Накамура, генеральный директор; Кардосо, Греция; Мартинес, А.С. (2020). «Улучшенные уравнения восприимчивости – инфекционности – восприимчивости к эпидемии, основанные на неопределенностях и автокорреляционных функциях». Королевское общество открытой науки . 7 (2): 191504. Бибкод : 2020RSOS....791504N. дои : 10.1098/rsos.191504. ПМК 7062106 . ПМИД  32257317. 
28. «(стр. 19) Модель SI» (PDF) .
29. Аль-Раи, Марван (2021). «Основное воспроизводственное число новой пандемии коронавируса со смертностью для Индии, Сирийской Арабской Республики, США, Йемена, Китая, Франции, Нигерии и России с разным уровнем заболеваемости». Клиническая эпидемиология и глобальное здоровье . 9 : 147–149. doi :10.1016/j.cegh.2020.08.005. ISSN  2452-0918. ПМЦ 7438206 . ПМИД  32844133. 
30. Первое и второе дифференциальные уравнения преобразуются и приводятся к тому же виду, что и для модели SIR выше.
31. Шликайзер Р., Крегер М. (2021). «Аналитическое моделирование временной эволюции вспышек эпидемий с учетом вакцинации». Физика . 3 (2): 386. Бибкод : 2021Physi...3..386S. дои : 10.3390/физика3020028 . hdl : 20.500.11850/487253 . S2CID  233589998.
32. Шликайзер Р., Крегер М. (2024). «Математика эпидемий: общее решение моделей SIRVD, SIRV, SIRD и SIR». Математика . 12 : 941. дои : 10.3390/math12070941 . hdl : 20.500.11850/665745 .
33. Хунцикер П. (24 июля 2021 г.). «Вакцинация против Covid-19 с персонализированной дозой на волне вируса. Вызывающие обеспокоенность варианты: обмен индивидуальной эффективностью на общественную пользу». Прецизионная наномедицина . 4 (3): 805–820. дои : 10.33218/001c.26101 .
34. Благородное СП (август 1974 г.). «Географическое и временное развитие чумы». Природа . 250 (5469): 726–729. Бибкод : 1974Natur.250..726N. дои : 10.1038/250726a0. PMID  4606583. S2CID  4210869.
35. Те Вругт М., Бикманн Дж., Витковски Р. (ноябрь 2020 г.). «Влияние социального дистанцирования и изоляции на распространение эпидемии, смоделированное с помощью теории функционала динамической плотности». Природные коммуникации . 11 (1): 5576. arXiv : 2003.13967 . Бибкод : 2020NatCo..11.5576T. дои : 10.1038/s41467-020-19024-0 . ПМЦ 7643184 . ПМИД  33149128. 
36. Хунцикер П. (07.03.2021). «Стратегии вакцинации для минимизации смертности от Covid-19 в Европе, где нет вакцин». medRxiv 10.1101/2021.01.29.21250747 . 
37. Croccolo F, Роман HE (октябрь 2020 г.). «Распространение инфекций по случайным графам: модель перколяции для COVID-19». Хаос, солитоны и фракталы . 139 : 110077. arXiv : 2006.10490 . Бибкод : 2020CSF...13910077C. doi :10.1016/j.chaos.2020.110077. ПМЦ 7332959 . PMID  32834619. S2CID  219792089. 
38. Кастальский, И.А.; Панкратова Е.В.; Миркес, Э.М.; и другие. (2021). «Социальный стресс определяет многоволновую динамику вспышек COVID-19». Научные отчеты . 11 (1): 22497. arXiv : 2106.08966 . Бибкод : 2021NatSR..1122497K. дои : 10.1038/s41598-021-01317-z . ПМЦ 8602246 . ПМИД  34795311. 
39. Репозиторий данных о COVID-19. Центр системных наук и инженерии (CSSE) Университета Джонса Хопкинса (JHU); предварительно обработанные данные находятся здесь: проект World in Data.
40. Паксон, Вэй; Шен, Бо-Вэнь (01 октября 2022 г.). «Уравнение КдВ – СИР и его аналитические решения для уединенных эпидемических волн». Международный журнал бифуркации и хаоса . 32 (13): 2250199–2250780. Бибкод : 2022IJBC...3250199P. дои : 10.1142/S0218127422501991. ISSN  0218-1274. S2CID  253314121.
41. Гао С., Тенг З., Ньето Дж.Дж., Торрес А. (2007). «Анализ модели эпидемии SIR с пульсовой вакцинацией и распределенной задержкой по времени». Журнал биомедицины и биотехнологии . 2007 : 64870. doi : 10.1155/2007/64870 . ПМК 2217597 . ПМИД  18322563. 
42. Дикманн, О.; Хестербек, Япония; Мец, JAJ (1 июня 1990 г.). «Об определении и расчете базового коэффициента воспроизводства R0 в моделях инфекционных заболеваний в гетерогенных популяциях». Журнал математической биологии . 28 (4): 365–382. дои : 10.1007/BF00178324. hdl : 1874/8051 . ISSN  1432-1416. PMID  2117040. S2CID  22275430.
43. Хеффернан, Дж. М.; Смит, Р.Дж.; Валь, Л.М. (22 сентября 2005 г.). «Перспективы базового репродуктивного соотношения». Журнал интерфейса Королевского общества . 2 (4): 281–293. дои : 10.1098/rsif.2005.0042. ISSN  1742-5689. ПМЦ 1578275 . ПМИД  16849186. 
44. ван ден Дриссе, П.; Уотмо, Джеймс (1 ноября 2002 г.). «Числа воспроизводства и подпороговое эндемическое равновесие для компартментальных моделей передачи болезней». Математические биологические науки . 180 (1): 29–48. дои : 10.1016/S0025-5564(02)00108-6. ISSN  0025-5564. PMID  12387915. S2CID  17313221.
45. Дж. Х. Джонс, Заметки о R0. Стэнфордский университет (2007 г.).
46. Дикманн, Одо; Хестербек, Ганс; Бриттон, Том (18 ноября 2012 г.). Математические инструменты для понимания динамики инфекционных заболеваний. Издательство Принстонского университета. ISBN 978-0-691-15539-5.
47. ван ден Дриссе, П.; Уотмо, Джеймс (2008), Брауэр, Фред; ван ден Дриссе, Полина; Ву, Цзяньхун (ред.), «Дальнейшие замечания по базовому числу воспроизводства», Математическая эпидемиология , Конспекты лекций по математике, том. 1945, Берлин, Гейдельберг: Springer, стр. 159–178, номер документа : 10.1007/978-3-540-78911-6_6, ISBN. 978-3-540-78911-6, получено 8 ноября 2022 г.
48. Дикманн О, Хестербек Дж.А., Мец Дж.А. (1990). «Об определении и расчете основного коэффициента воспроизводства R0 в моделях инфекционных заболеваний в гетерогенных популяциях». Журнал математической биологии . 28 (4): 365–82. дои : 10.1007/BF00178324. hdl : 1874/8051 . PMID  2117040. S2CID  22275430.
49. Воль С., Шаффнер С.Ф., Сабети ПК (сентябрь 2016 г.). «Геномный анализ вирусных вспышек». Ежегодный обзор вирусологии . 3 (1): 173–195. doi : 10.1146/annurev-virology-110615-035747. ПМК 5210220 . ПМИД  27501264. 
50. Липсич М., Коэн Т., Купер Б., Робинс Дж.М., Ма С., Джеймс Л. и др. (июнь 2003 г.). «Динамика передачи и контроль тяжелого острого респираторного синдрома». Наука . 300 (5627): 1966–70. Бибкод : 2003Sci...300.1966L. дои : 10.1126/science.1086616. ПМК 2760158 . ПМИД  12766207. 
51. Рихан, Фаталла А.; Анвар, М. Наим (2012). «Качественный анализ модели отсроченной эпидемии SIR с насыщенным уровнем заболеваемости». Международный журнал дифференциальных уравнений . 2012 : 1–13. дои : 10.1155/2012/408637 .
52. Блоуэр С.М., Маклин А.Р., Порко Т.К., Смолл П.М., Хоупвелл ПК, Санчес М.А., Мосс А.Р. (август 1995 г.). «Внутренняя динамика передачи эпидемий туберкулеза». Природная медицина . 1 (8): 815–21. дои : 10.1038/nm0895-815. PMID  7585186. S2CID  19795498.
53. Ма Ю, Хорсбург CR, Уайт LF, Дженкинс HE (сентябрь 2018 г.). «Количественная оценка передачи туберкулеза: систематический обзор репродуктивного числа и оценок серийных интервалов туберкулеза». Эпидемиология и инфекции . 146 (12): 1478–1494. дои : 10.1017/S0950268818001760. ПМК 6092233 . ПМИД  29970199. 
54. Брауэр Ф, Кастильо-Чавес С (2001). Математические модели в популяционной биологии и эпидемиологии . Нью-Йорк: Спрингер. ISBN 0-387-98902-1.
55. Для получения дополнительной информации об этом типе модели см. Anderson RM , ed. (1982). Популяционная динамика инфекционных болезней: теория и приложения . Лондон-Нью-Йорк: Чепмен и Холл. ISBN 0-412-21610-8.
56. Тембине, Х (2020). «COVID-19: Перспектива игры типа среднего поля, основанная на данных». Журнал игр . 11, 51 (4): 1–111 . Проверено 24 ноября 2022 г.
57. Бартлетт М.С. (1957). «Периодичность кори и размер сообщества». Журнал Королевского статистического общества, серия A. 120 (1): 48–70. дои : 10.2307/2342553. JSTOR  2342553. S2CID  91114210.
58. Мэй РМ, Ллойд А.Л. (декабрь 2001 г.). «Динамика заражения в безмасштабных сетях». Физический обзор E . 64 (6 Pt 2): 066112. Бибкод : 2001PhRvE..64f6112M. doi : 10.1103/PhysRevE.64.066112. ПМИД  11736241.
59. Пастор-Саторрас Р., Веспиньяни А. (апрель 2001 г.). «Распространение эпидемии в безмасштабных сетях». Письма о физических отзывах . 86 (14): 3200–3203. arXiv : cond-mat/0010317 . Бибкод : 2001PhRvL..86.3200P. doi : 10.1103/PhysRevLett.86.3200. hdl : 2117/126209. PMID  11290142. S2CID  16298768.
60. Ньюман М.Э. (июль 2002 г.). «Распространение эпидемического заболевания в сетях». Физический обзор E . 66 (1 Pt 2): 016128. arXiv : cond-mat/0205009 . Бибкод : 2002PhRvE..66a6128N. doi : 10.1103/PhysRevE.66.016128. PMID  12241447. S2CID  15291065.
61. Вонг Ф., Коллинз Джей-Джей (ноябрь 2020 г.). «Доказательства того, что суперраспространение коронавируса носит толстый хвост». Труды Национальной академии наук Соединенных Штатов Америки . 117 (47): 29416–29418. Бибкод : 2020PNAS..11729416W. дои : 10.1073/pnas.2018490117 . ПМЦ 7703634 . PMID  33139561. S2CID  226242440. 

дальнейшее чтение

• Мэй Р.М. , Андерсон Р.М. (1991). Инфекционные болезни человека: динамика и борьба . Оксфорд: Издательство Оксфордского университета. ISBN 0-19-854040-Х.
• Винницкий Е., Белый Р.Г., ред. (2010). Введение в моделирование инфекционных заболеваний . Оксфорд: Издательство Оксфордского университета. ISBN 978-0-19-856576-5.
• Капассо V (2008). Математические структуры эпидемических систем. 2-я печать . Гейдельберг: Спрингер. ISBN 978-3-540-56526-0.
• Карлсон К.С., Рубин Д.М., Хейккиля В., Постема М. (2021). «Извлечение параметров передачи и восстановления для модели адаптивной глобальной системной динамики пандемии COVID-19». IEEE Африка, 2021 г. (PDF) . стр. 456–459. doi : 10.1109/AFRICON51333.2021.9570946. ISBN 978-1-6654-1984-0. S2CID  239899862.

Внешние ссылки

• Модель SIR: онлайн-эксперименты с JSXGraph
• «Имитация эпидемии». 3Синий1Коричневый . 27 марта 2020 г. — через YouTube .