Нечеткая логика

Нечеткая логика — это форма многозначной логики , в которой истинностное значение переменных может быть любым действительным числом от 0 до 1. Она применяется для обработки концепции частичной истины, где истинностное значение может находиться в диапазоне от полностью истинного до полностью ложного. ^[1] Напротив, в булевой логике истинностные значения переменных могут быть только целыми числами 0 или 1.

Термин «нечеткая логика» был введен в 1965 году в предложении теории нечетких множеств математиком Лотфи Заде . ^[2]^[3] Однако нечеткая логика изучалась с 1920-х годов как бесконечнозначная логика — в частности, Лукасевичем и Тарским . ^[4]

Нечеткая логика основана на наблюдении, что люди принимают решения на основе неточной и нечисловой информации. Нечеткие модели или нечеткие множества являются математическими средствами представления неопределенности и неточной информации (отсюда и термин нечеткий). Эти модели обладают способностью распознавать, представлять, манипулировать, интерпретировать и использовать данные и информацию, которые являются неопределенными и не имеют определенности. ^[5]^[6]

Нечеткая логика применяется во многих областях: от теории управления до искусственного интеллекта .

Обзор

Классическая логика допускает только выводы, которые являются либо истинными, либо ложными. Однако существуют также предложения с переменными ответами, которые можно обнаружить, если попросить группу людей определить цвет. В таких случаях истина появляется как результат рассуждения из неточного или частичного знания, в котором выборочные ответы отображаются в спектре. ^[7]

Как степень истинности , так и вероятность находятся в диапазоне от 0 до 1 и, следовательно, на первый взгляд могут показаться идентичными, но нечеткая логика использует степень истинности как математическую модель неопределенности , в то время как вероятность является математической моделью незнания . ^[8]

Применение значений истинности

Базовое приложение может характеризовать различные поддиапазоны непрерывной переменной . Например, измерение температуры для антиблокировочной системы тормозов может иметь несколько отдельных функций принадлежности, определяющих конкретные диапазоны температур, необходимые для надлежащего управления тормозами. Каждая функция сопоставляет одно и то же значение температуры со значением истины в диапазоне от 0 до 1. Эти значения истины затем можно использовать для определения того, как следует управлять тормозами. ^[9] Теория нечетких множеств предоставляет средства для представления неопределенности.

Лингвистические переменные

В приложениях нечеткой логики нечисловые значения часто используются для облегчения выражения правил и фактов. ^[10]

Лингвистическая переменная, такая как возраст, может принимать такие значения, как молодой и его антоним старый . Поскольку естественные языки не всегда содержат достаточно терминов значений для выражения нечеткой шкалы значений, общепринятой практикой является изменение лингвистических значений с помощью прилагательных или наречий . Например, мы можем использовать хеджи скорее и несколько для построения дополнительных значений скорее старый или несколько молодой . ^[11]

Нечеткие системы

Мамдани

Наиболее известная система — система, основанная на правилах Мамдани . ^[12] Она использует следующие правила:

Преобразовать все входные значения в нечеткие функции принадлежности.
Выполнить все применимые правила в базе правил для вычисления нечетких выходных функций.
Устраните нечеткость нечетких выходных функций, чтобы получить «четкие» выходные значения.

Фаззификация

Фаззификация — это процесс присвоения числового входа системы нечетким множествам с некоторой степенью принадлежности. Эта степень принадлежности может быть где угодно в пределах интервала [0,1]. Если она равна 0, то значение не принадлежит данному нечеткому множеству, а если она равна 1, то значение полностью принадлежит нечеткому множеству. Любое значение между 0 и 1 представляет собой степень неопределенности того, что значение принадлежит набору. Эти нечеткие множества обычно описываются словами, и поэтому, присваивая вход системы нечетким множествам, мы можем рассуждать с ним лингвистически естественным образом.

Например, на изображении ниже значения выражений cold , warm и hot представлены функциями, отображающими температурную шкалу. Точка на этой шкале имеет три «значения истинности» — по одному для каждой из трех функций. Вертикальная линия на изображении представляет собой определенную температуру, которую измеряют три стрелки (значения истинности). Поскольку красная стрелка указывает на ноль, эта температура может быть интерпретирована как «не горячая»; т. е. эта температура имеет нулевое членство в нечетком множестве «горячая». Оранжевая стрелка (указывающая на 0,2) может описывать ее как «слегка теплая», а синяя стрелка (указывающая на 0,8) — «довольно холодная». Следовательно, эта температура имеет 0,2 членства в нечетком множестве «теплая» и 0,8 членства в нечетком множестве «холодная». Степень членства, назначенная для каждого нечеткого множества, является результатом фаззификации.

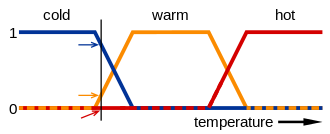
Нечеткие множества часто определяются как треугольные или трапециевидные кривые, поскольку каждое значение будет иметь наклон, где значение увеличивается, пик, где значение равно 1 (который может иметь длину 0 или больше), и наклон, где значение уменьшается. ^[13] Их также можно определить с помощью сигмоидальной функции . ^[14] Одним из распространенных случаев является стандартная логистическая функция, определяемая как

S(x)={\frac {1}{1+e^{-x}}}

который имеет следующее свойство симметрии

S(x)+S(-x)=1.

Из этого следует, что

$(S(x)+S(-x))\cdot (S(y)+S(-y))\cdot (S(z)+S(-z))=1$

Нечеткие логические операторы

Нечеткая логика работает со значениями членства способом, который имитирует булеву логику . Для этого должны быть доступны замены для базовых операторов («ворот») AND, OR, NOT. Есть несколько способов сделать это. Распространенная замена называетсяОператоры Заде :

Для значений ИСТИНА/1 и ЛОЖЬ/0 нечеткие выражения дают тот же результат, что и булевы выражения.

Существуют также другие операторы, более лингвистические по своей природе, называемые хеджами , которые могут применяться. Это, как правило, наречия, такие как very или several , которые изменяют значение множества с помощью математической формулы . ^[15]

Однако произвольная таблица выбора не всегда определяет нечеткую логическую функцию. В статье (Зайцев и др.) ^[16] был сформулирован критерий, позволяющий распознать, определяет ли данная таблица выбора нечеткую логическую функцию, и предложен простой алгоритм синтеза нечеткой логической функции на основе введенных понятий составляющих минимума и максимума. Нечеткая логическая функция представляет собой дизъюнкцию составляющих минимума, где составляющей минимума является конъюнкция переменных текущей области, больших или равных значению функции в этой области (справа от значения функции в неравенстве, включая значение функции).

Другой набор операторов И/ИЛИ основан на умножении, где

х И у = х*уНЕ х = 1 - хСледовательно,x ИЛИ y = НЕ( И( НЕ(x), НЕ(y) ) )x ИЛИ y = НЕ( И(1-x, 1-y) )x ИЛИ y = НЕ( (1-x)*(1-y) )x ИЛИ y = 1-(1-x)*(1-y)х ИЛИ у = х+у-ху

Учитывая любые два из AND/OR/NOT, можно вывести третий. Обобщение AND является примером t-нормы .

ЕСЛИ-ТО правила

Правила IF-THEN сопоставляют входные или вычисленные значения истинности с желаемыми выходными значениями истинности. Пример:

ЕСЛИ температура очень низкая, ТО fan_speed останавливаетсяЕСЛИ температура низкая, ТО скорость вентилятора низкаяЕСЛИ температура высокая, ТО скорость вентилятора умереннаяЕСЛИ температура высокая, ТО скорость вентилятора высокая

При определенной температуре нечеткая переменная hot имеет определенное значение истинности, которое копируется в переменную high .

Если выходная переменная встречается в нескольких частях THEN, то значения из соответствующих частей IF объединяются с помощью оператора OR.

Дефаззификация

Цель состоит в том, чтобы получить непрерывную переменную из нечетких значений истинности. ^{[ необходима ссылка ]}

Это было бы легко, если бы выходные значения истинности были точно такими, которые получены в результате фаззификации заданного числа. Однако, поскольку все выходные значения истинности вычисляются независимо, в большинстве случаев они не представляют собой такой набор чисел. ^{[ необходима цитата ]} Затем нужно выбрать число, которое лучше всего соответствует «намерению», закодированному в значении истинности. Например, для нескольких значений истинности fan_speed необходимо найти фактическую скорость, которая лучше всего соответствует вычисленным значениям истинности переменных «медленный», «умеренный» и т. д. ^{[ необходима цитата ]}

Единого алгоритма для этой цели не существует.

Обычный алгоритм —

Для каждого значения истинности, сократить функцию принадлежности до этого значения
Объедините полученные кривые с помощью оператора ИЛИ.
Найдите центр тяжести области под кривой
Положение x этого центра затем является конечным результатом.

Такаги–Сугэно–Канг (TSK)

Система TSK ^[17] похожа на Мамдани, но процесс дефаззификации включен в выполнение нечетких правил. Они также адаптированы, так что вместо этого консеквент правила представлен через полиномиальную функцию (обычно постоянную или линейную). Примером правила с постоянным выходом будет:

ЕСЛИ температура очень низкая = 2

В этом случае вывод будет равен константе консеквента (например, 2). В большинстве сценариев у нас будет полная база правил с 2 или более правилами. Если это так, вывод всей базы правил будет средним значением консеквента каждого правила i (Y _i ), взвешенным в соответствии со значением членства его антецедента (h _i ):

${\frac {\sum _{i}(h_{i}\cdot Y_{i})}{\sum _{i}h_{i}}}$

Примером правила с линейным выходом может быть:

ЕСЛИ температура очень низкая И влажность высокая = 2 * температура + 1 * влажность

В этом случае вывод правила будет результатом функции в консеквенте. Переменные внутри функции представляют значения членства после фаззификации, а не четкие значения. Как и прежде, в случае, если у нас есть полная база правил с 2 или более правилами, общий вывод будет взвешенным средним между выводами каждого правила.

Главное преимущество использования TSK по сравнению с Mamdani заключается в том, что он эффективен с точки зрения вычислений и хорошо работает в других алгоритмах, таких как ПИД-регулирование и с алгоритмами оптимизации. Он также может гарантировать непрерывность выходной поверхности. Однако Mamdani более интуитивен и прост в работе для людей. Поэтому TSK обычно используется в других сложных методах, таких как адаптивные нейро-нечеткие системы вывода .

Формирование консенсуса входных данных и нечетких правил

Поскольку выход нечеткой системы является консенсусом всех входов и всех правил, системы нечеткой логики могут хорошо себя вести, когда входные значения недоступны или не заслуживают доверия. Веса могут быть опционально добавлены к каждому правилу в базе правил, и веса могут использоваться для регулирования степени, в которой правило влияет на выходные значения. Эти веса правил могут быть основаны на приоритете, надежности или согласованности каждого правила. Эти веса правил могут быть статическими или могут быть изменены динамически, даже на основе выходных данных других правил.

Приложения

Нечеткая логика используется в системах управления, чтобы позволить экспертам вносить нечеткие правила, например, «если вы близко к станции назначения и движетесь быстро, увеличьте давление тормозов поезда»; эти нечеткие правила затем могут быть численно уточнены в системе.

Многие из ранних успешных приложений нечеткой логики были реализованы в Японии. Первое заметное применение было в серии Sendai Subway 1000 , в которой нечеткая логика смогла улучшить экономичность, комфорт и точность поездки. Она также использовалась для распознавания рукописного ввода в карманных компьютерах Sony, в средствах управления полетом вертолетов, в управлении системой метрополитена, для повышения топливной экономичности автомобилей, в управлении стиральными машинами с одной кнопкой, в автоматическом управлении питанием в пылесосах и в раннем распознавании землетрясений через Институт сейсмологии Бюро метеорологии, Япония. ^[18]

Искусственный интеллект

Нейронные сети на основе искусственного интеллекта и нечеткой логики при анализе являются одним и тем же — базовая логика нейронных сетей нечеткая. Нейронная сеть будет принимать различные значимые входные данные, давать им разные веса по отношению друг к другу, комбинировать промежуточные значения определенное количество раз и приходить к решению с определенным значением. Нигде в этом процессе нет ничего похожего на последовательности решений «или-или», которые характеризуют нечеткую математику, компьютерное программирование и цифровую электронику . В 1980-х годах исследователи разделились во мнениях о наиболее эффективном подходе к машинному обучению : обучение на основе дерева решений или нейронные сети. Первый подход использует двоичную логику, сопоставляя оборудование, на котором он работает, но, несмотря на большие усилия, он не привел к созданию интеллектуальных систем. Нейронные сети, напротив, привели к точным моделям сложных ситуаций и вскоре нашли свой путь во множество электронных устройств. ^[19] Теперь их также можно реализовать непосредственно на аналоговых микросхемах, в отличие от предыдущих псевдоаналоговых реализаций на цифровых микросхемах. Более высокая эффективность этих устройств компенсирует присущую им меньшую точность аналоговых устройств в различных вариантах использования.

Принятие медицинских решений

Нечеткая логика является важной концепцией в принятии медицинских решений . Поскольку медицинские и санитарные данные могут быть субъективными или нечеткими, приложения в этой области имеют большой потенциал для получения большой выгоды от использования подходов, основанных на нечеткой логике.

Нечеткая логика может использоваться во многих различных аспектах в рамках принятия медицинских решений. Такие аспекты включают ^[20]^[21]^[22]^{[ необходимо разъяснение ]} в анализе медицинских изображений , анализе биомедицинских сигналов, сегментации изображений ^[23] или сигналов, а также извлечении признаков /выборе изображений ^[23] или сигналов. ^[24]

Самый большой вопрос в этой области применения — сколько полезной информации можно получить при использовании нечеткой логики. Основная проблема — как получить требуемые нечеткие данные. Это становится еще сложнее, когда приходится получать такие данные от людей (обычно пациентов). Как уже было сказано

«Как ни парадоксально, границы того, что может быть достигнуто и чего не может быть достигнуто в медицинской диагностике, сами по себе размыты»
— Семь вызовов, 2019. ^[25]

Как извлекать нечеткие данные и как проверять точность данных, все еще является продолжающейся работой, тесно связанной с применением нечеткой логики. Проблема оценки качества нечетких данных является сложной. Вот почему нечеткая логика является весьма многообещающей возможностью в области применения принятия медицинских решений, но все еще требует дополнительных исследований для раскрытия ее полного потенциала. ^[25]

Компьютерная диагностика на основе изображений

Одной из распространенных областей применения нечеткой логики является компьютерная диагностика на основе изображений в медицине. ^[26] Компьютерная диагностика представляет собой компьютеризированный набор взаимосвязанных инструментов, которые могут использоваться для оказания помощи врачам в принятии диагностических решений.

Нечеткие базы данных

После определения нечетких отношений можно разрабатывать нечеткие реляционные базы данных . Первая нечеткая реляционная база данных, FRDB, появилась в диссертации Марии Земанковой (1983). Позже возникли и другие модели, такие как модель Баклза-Петри, модель Праде-Тестемейла, модель Умано-Фуками или модель GEFRED Дж. М. Медины, М. А. Вилы и др.

Были определены нечеткие языки запросов, такие как SQLf П. Боска и др. и FSQL Дж. Галиндо и др. Эти языки определяют некоторые структуры для включения нечетких аспектов в операторы SQL, такие как нечеткие условия, нечеткие компараторы, нечеткие константы, нечеткие ограничения, нечеткие пороги, лингвистические метки и т. д.

Логический анализ

В математической логике существует несколько формальных систем «нечеткой логики», большинство из которых относятся к семейству нечетких логик t-нормы .

Пропозициональная нечеткая логика

Наиболее важными пропозициональными нечеткими логиками являются:

Моноидальная пропозициональная нечеткая логика на основе t-нормы MTL является аксиоматизацией логики, где конъюнкция определяется левой непрерывной t-нормой , а импликация определяется как остаток t-нормы. Ее модели соответствуют MTL-алгебрам, которые являются предлинейными коммутативными ограниченными целочисленными решетками с вычетом .
Базовая пропозициональная нечеткая логика BL является расширением логики MTL, где конъюнкция определяется непрерывной t-нормой, а импликация также определяется как остаток t-нормы. Ее модели соответствуют BL-алгебрам.
Нечеткая логика Лукасевича является расширением базовой нечеткой логики BL, где стандартная конъюнкция — это t-норма Лукасевича. Она имеет аксиомы базовой нечеткой логики плюс аксиому двойного отрицания, а ее модели соответствуют MV-алгебрам .
Нечеткая логика Гёделя является расширением базовой нечеткой логики BL, где конъюнкция является t-нормой Гёделя (то есть минимумом). Она имеет аксиомы BL плюс аксиому идемпотентности конъюнкции, а ее модели называются G-алгебрами.
Нечеткая логика продукта является расширением базовой нечеткой логики BL, где конъюнкция является t-нормой продукта. Она имеет аксиомы BL плюс еще одну аксиому для сокращаемости конъюнкции, а ее модели называются алгебрами продукта.
Нечеткая логика с оцениваемым синтаксисом (иногда также называемая логикой Павелки), обозначаемая EVL, является дальнейшим обобщением математической нечеткой логики. В то время как указанные выше виды нечеткой логики имеют традиционный синтаксис и многозначную семантику, в EVL синтаксис также оценивается. Это означает, что каждая формула имеет оценку. Аксиоматизация EVL вытекает из нечеткой логики Лукасевича. Обобщение классической теоремы Гёделя о полноте доказуемо в EVL ^{[ требуется цитата ]} .

Предикатная нечеткая логика

Подобно тому, как предикатная логика создается из пропозициональной логики , предикатные нечеткие логики расширяют нечеткие системы с помощью универсальных и экзистенциальных кванторов . Семантика универсального квантора в t-нормальных нечетких логиках является инфимумом степеней истинности экземпляров квантифицированной подформулы, в то время как семантика экзистенциального квантора является супремумом того же самого.

Проблемы разрешимости

Понятия «разрешимого подмножества» и « рекурсивно перечислимого подмножества» являются базовыми для классической математики и классической логики . Таким образом, вопрос об их подходящем расширении до теории нечетких множеств является ключевым. Первое предложение в этом направлении было сделано Э. С. Сантосом с помощью понятий нечеткой машины Тьюринга , нормального нечеткого алгоритма Маркова и нечеткой программы (см. Santos 1970). Впоследствии Л. Биачино и Дж. Герла утверждали, что предложенные определения довольно сомнительны. Например, в ^[27] показано, что нечеткие машины Тьюринга не подходят для теории нечетких языков, поскольку существуют естественные нечеткие языки, интуитивно вычислимые, которые не могут быть распознаны нечеткой машиной Тьюринга. Затем они предложили следующие определения. Обозначим через Ü множество рациональных чисел в [0,1]. Тогда нечеткое подмножество s : S [0,1] множества S рекурсивно перечислимо, если существует рекурсивное отображение h : S × N Ü такое, что для каждого x из S функция h ( x , n ) возрастает по n и s ( x ) = lim h ( x , n ). Мы говорим, что s разрешимо , если и s , и его дополнение – s рекурсивно перечислимы. Возможно расширение такой теории на общий случай L-подмножеств (см. Gerla 2006). Предложенные определения хорошо связаны с нечеткой логикой. Действительно, следующая теорема верна (при условии, что аппарат вывода рассматриваемой нечеткой логики удовлетворяет некоторому очевидному свойству эффективности). $\rightarrow$ $\rightarrow$

Любая "аксиоматизируемая" нечеткая теория рекурсивно перечислима. В частности, нечеткое множество логически истинных формул рекурсивно перечислимо, несмотря на то, что четкое множество допустимых формул, вообще говоря, не является рекурсивно перечислимым. Более того, любая аксиоматизируемая и полная теория разрешима.

Открытым вопросом является поддержка "тезиса Чёрча" для нечёткой математики , предложенное понятие рекурсивной перечислимости для нечётких подмножеств является адекватным. Для решения этой проблемы необходимо расширение понятий нечёткой грамматики и нечёткой машины Тьюринга . Другой открытый вопрос заключается в том, чтобы начать с этого понятия и найти расширение теорем Гёделя на нечёткую логику.

По сравнению с другими логиками

Вероятность

Нечеткая логика и вероятность рассматривают различные формы неопределенности. В то время как нечеткая логика и теория вероятностей могут представлять степени определенных видов субъективных убеждений, теория нечетких множеств использует концепцию членства в нечетком множестве, т. е. насколько наблюдение находится в пределах нечетко определенного множества, а теория вероятностей использует концепцию субъективной вероятности , т. е. частоты возникновения или вероятности некоторого события или условия ^{[ необходимо разъяснение ]} . Концепция нечетких множеств была разработана в середине двадцатого века в Беркли ^[28] в ответ на отсутствие теории вероятностей для совместного моделирования неопределенности и неопределенности . ^[29]

Барт Коско утверждает в работе «Нечеткость против вероятности ^{» [30]} , что теория вероятностей является подтеорией нечеткой логики, поскольку вопросы степеней веры во взаимоисключающее членство множеств в теории вероятностей могут быть представлены как определенные случаи невзаимноисключающего градуированного членства в нечеткой теории. В этом контексте он также выводит теорему Байеса из концепции нечеткого подмножества. Лотфи А. Заде утверждает, что нечеткая логика отличается по характеру от вероятности и не является ее заменой. Он нечетко определил вероятность как нечеткую вероятность, а также обобщил ее до теории возможностей . ^[31]

В более общем смысле нечеткая логика — это одно из многих различных расширений классической логики, призванных решать вопросы неопределенности, выходящие за рамки классической логики, неприменимости теории вероятностей во многих областях и парадоксов теории Демпстера–Шейфера .

Экоритмы

Теоретик вычислений Лесли Валиант использует термин экоритмы для описания того, как много менее точных систем и методов, таких как нечеткая логика (и «менее надежная» логика), могут быть применены к алгоритмам обучения . Валиант по сути переопределяет машинное обучение как эволюционное. В общем смысле, экоритмы — это алгоритмы, которые обучаются на своих более сложных средах (отсюда и эко- ), чтобы обобщать, аппроксимировать и упрощать логику решения. Как и нечеткая логика, они представляют собой методы, используемые для преодоления непрерывных переменных или систем, слишком сложных для полного перечисления или понимания дискретно или точно. ^[32] Экоритмы и нечеткая логика также имеют общее свойство иметь дело с возможностями больше, чем с вероятностями, хотя обратная связь и прямая связь , в основном стохастические веса, являются особенностью обоих при работе, например, с динамическими системами .

Гёдель Г.∞логика

Другая логическая система, где значения истинности являются действительными числами от 0 до 1 и где операторы AND и OR заменены на MIN и MAX, — это логика G _∞ Гёделя . Эта логика имеет много общего с нечеткой логикой, но определяет отрицание по-другому и имеет внутреннюю импликацию. Отрицание и импликация определяются следующим образом: $\neg _{G}$ ${\xrightarrow[{G}]{}}$

{\begin{align}\neg _{G}u&={\begin{cases}1,&{\text{if }}u=0\\0,&{\text{if }}u>0\end{cases}}\\[3pt]u\mathrel {\xrightarrow[{G}]{}} v&={\begin{cases}1,&{\text{if }}u\leq v\\v,&{\text{if }}u>v\end{cases}}\end{align}}

что превращает полученную логическую систему в модель для интуиционистской логики , делая ее особенно хорошо себя ведущей среди всех возможных выборов логических систем с действительными числами от 0 до 1 в качестве значений истинности. В этом случае импликация может быть интерпретирована как «x менее истинен, чем y», а отрицание — как «x менее истинен, чем 0» или «x строго ложно», и для любого и мы имеем, что . В частности, в логике Гёделя отрицание больше не является инволюцией, а двойное отрицание отображает любое ненулевое значение в 1. $x$ $y$ $AND(x,x\mathrel {\xrightarrow[{G}]{}} y)=AND(x,y)$

Компенсационная нечеткая логика

Компенсационная нечеткая логика (CFL) — это раздел нечеткой логики с измененными правилами для конъюнкции и дизъюнкции. Когда истинностное значение одного компонента конъюнкции или дизъюнкции увеличивается или уменьшается, другой компонент уменьшается или увеличивается для компенсации. Это увеличение или уменьшение истинностного значения может быть компенсировано увеличением или уменьшением другого компонента. Смещение может быть заблокировано при достижении определенных пороговых значений. Сторонники ^{[ who? ]} утверждают, что CFL обеспечивает лучшее вычислительное семантическое поведение и имитирует естественный язык. ^{[ неопределенно ]}^[33]^[34]

Согласно Хесусу Сехасу Монтеро (2011), компенсационная нечеткая логика состоит из четырех непрерывных операторов: конъюнкция (c); дизъюнкция (d); нечеткий строгий порядок (or); и отрицание (n). Конъюнкция является геометрическим средним и его дуальными как конъюнктивные и дизъюнктивные операторы. ^[35]

Стандартизация языка разметки

IEEE 1855 , IEEE STANDARD 1855–2016, посвящен языку спецификаций под названием Fuzzy Markup Language (FML) ^[36], разработанному Ассоциацией стандартов IEEE . FML позволяет моделировать систему нечеткой логики в удобном для восприятия человеком и независимом от оборудования виде. FML основан на расширяемом языке разметки ( XML ). Разработчики нечетких систем с FML имеют унифицированную и высокоуровневую методологию для описания совместимых нечетких систем. IEEE STANDARD 1855–2016 использует язык определения W3C XML Schema для определения синтаксиса и семантики программ FML.

До внедрения FML специалисты по нечеткой логике могли обмениваться информацией о своих нечетких алгоритмах, добавляя к своим программным функциям возможность читать, правильно анализировать и сохранять результаты своей работы в форме, совместимой с языком нечеткого управления (FCL), описанным и указанным в части 7 стандарта IEC 61131. ^[37]^[38]

Смотрите также

Ссылки

^ Новак, В.; Перфильева И.; Мочкорж, Дж. (1999). Математические принципы нечеткой логики . Дордрехт: Клювер Академик. ISBN 978-0-7923-8595-0.
^ "Fuzzy Logic". Стэнфордская энциклопедия философии . Университет Брайанта. 23 июля 2006 г. Получено 30 сентября 2008 г.
^ Заде, LA (июнь 1965). «Нечеткие множества». Информация и управление . 8 (3). Сан-Диего: 338–353. doi : 10.1016/S0019-9958(65)90241-X . ISSN 0019-9958. Zbl 0139.24606. Wikidata Q25938993.
^ Пеллетье, Фрэнсис Джеффри (2000). «Обзор метаматематики нечеткой логики» (PDF) . Бюллетень символической логики . 6 (3): 342–346. doi :10.2307/421060. JSTOR 421060. Архивировано (PDF) из оригинала 3 марта 2016 г.
^ "Что такое нечеткая логика? "Форум по обсуждению машиностроения"". mechanicalsite.com . Архивировано из оригинала 11 ноября 2018 г. . Получено 11 ноября 2018 г. .{{cite web}}: CS1 maint: unfit URL (link)
^ Бабушка, Роберт (1998). Нечеткое моделирование для управления. Springer Science & Business Media. ISBN 978-94-011-4868-9.
^ "Fuzzy Logic". YouTube . 9 мая 2013 г. Архивировано из оригинала 5 декабря 2021 г. Получено 11 мая 2020 г.
^ Асли, Каве Харири; Алиев, Солтан Али Оглы; Томас, Сабу; Гопакумар, Дипу А. (23 ноября 2017 г.). Справочник по исследованиям в области механики жидкости и твердого тела: теория, моделирование и эксперимент. ЦРК Пресс. ISBN 9781315341507.
^ Чаудхури, Ариндам; Мандавия, Крупа; Баделия, Пратикса; Гош, Соумья К. (23 декабря 2016 г.). Системы оптического распознавания символов для разных языков с мягкими вычислениями. Springer. ISBN 9783319502526.
^ Заде, LA; и др. (1996). Нечеткие множества, нечеткая логика, нечеткие системы . World Scientific Press. ISBN 978-981-02-2421-9.
^ Заде, LA (январь 1975). «Концепция лингвистической переменной и ее применение к приближенным рассуждениям — I». Информационные науки . 8 (3): 199–249. doi :10.1016/0020-0255(75)90036-5.
^ Мамдани, Э. Х. (1974). «Применение нечетких алгоритмов для управления простым динамическим объектом». Труды Института инженеров-электриков . 121 (12): 1585–1588. doi :10.1049/PIEE.1974.0328.
^ Сяо, Чжи; Ся, Сиси; Гун, Кэ; Ли, Дэн (1 декабря 2012 г.). «Трапециевидное нечеткое мягкое множество и его применение в MCDM». Прикладное математическое моделирование . 36 (12): 5846–5847. doi : 10.1016/j.apm.2012.01.036 . ISSN 0307-904X.
^ Виерман, Марк Дж. «Введение в математику неопределенности: включая теорию множеств, логику, вероятность, нечеткие множества, грубые множества и теорию доказательств» (PDF) . Университет Крейтона. Архивировано (PDF) из оригинала 30 июля 2012 г. . Получено 16 июля 2016 г. .
^ Заде, LA (январь 1972). «Интерпретация лингвистических преград с точки зрения теории нечетких множеств». Журнал кибернетики . 2 (3): 4–34. doi :10.1080/01969727208542910. ISSN 0022-0280.
^ Зайцев, ДА; Сарбей, ВГ; Слепцов, АИ (1998). «Синтез функций непрерывной логики, заданных в табличной форме». Кибернетика и системный анализ . 34 (2): 190–195. doi :10.1007/BF02742068. S2CID 120220846.
^ Такаги, Томохиро; Сугено, Мичио (январь 1985 г.). «Нечеткая идентификация систем и ее применение в моделировании и управлении». Труды IEEE по системам, человеку и кибернетике . SMC-15 (1): 116–132. doi :10.1109/TSMC.1985.6313399. S2CID 3333100.
^ Бансод, Нитин А.; Кулкарни, Маршалл; Патил, С.Х. (2005). «Мягкие вычисления — подход нечеткой логики». В Bharati Vidyapeeth College of Engineering (ред.). Мягкие вычисления . Allied Publishers. стр. 73. ISBN 978-81-7764-632-0. Получено 9 ноября 2018 г.
^ Элкан, Чарльз (1994). «Парадоксальный успех нечеткой логики». IEEE Expert . 9 (4): 3–49. CiteSeerX 10.1.1.100.8402 . doi :10.1109/64.336150. S2CID 113687.
^ Линь, КП; Чанг, ХФ; Чэнь, ТЛ; Лу, ЙМ; Ванг, ЧХ (2016). «Интуиционистская нечеткая C-регрессия с использованием регрессии опорных векторов наименьших квадратов». Экспертные системы с приложениями . 64 : 296–304. doi :10.1016/j.eswa.2016.07.040.
^ Дэн, Х.; Дэн, В.; Сан, Х.; Йе, Ч.; Чжоу, Х. (2016). «Адаптивное интуиционистское нечеткое улучшение изображений МРТ опухолей мозга». Scientific Reports . 6 : 35760. Bibcode : 2016NatSR...635760D. doi : 10.1038/srep35760 . PMC 5082372. PMID 27786240 .
^ Влахос, IK; Сергиадис, GD (2007). «Интуиционистская нечеткая информация — приложения к распознаванию образов». Pattern Recognition Letters . 28 (2): 197–206. Bibcode : 2007PaReL..28..197V. doi : 10.1016/j.patrec.2006.07.004.
^ ab Гонсалес-Идальго, Мануэль; Мунар, Марк; Бибилони, Педро; Мойя-Альковер, Габриэль; Краус-Мигель, Андреа; Сегура-Сампедро, Хуан Хосе (октябрь 2019 г.). «Обнаружение инфицированных ран на изображениях абдоминальной хирургии с использованием нечеткой логики и нечетких множеств». Международная конференция по беспроводным и мобильным вычислениям, сетям и коммуникациям (WiMob) 2019 г. Барселона, Испания: IEEE. стр. 99–106. doi :10.1109/WiMOB.2019.8923289. ISBN 978-1-7281-3316-4. S2CID 208880793.
^ Дас, С.; Гуха, Д.; Дутта, Б. (2016). «Медицинская диагностика с помощью использования нечеткой логики и интуиционистской нечеткой логики». Applied Intelligence . 45 (3): 850–867. doi :10.1007/s10489-016-0792-0. S2CID 14590409.
^ ab Yanase, Juri; Triantaphyllou, Evangelos (2019). «Семь ключевых проблем будущего компьютерной диагностики в медицине». Международный журнал медицинской информатики . 129 : 413–422. doi : 10.1016/j.ijmedinf.2019.06.017. PMID 31445285. S2CID 198287435.
^ Yanase, Juri; Triantaphyllou, Evangelos (2019). «Систематическое исследование компьютерной диагностики в медицине: прошлое и настоящее». Экспертные системы с приложениями . 138 : 112821. doi : 10.1016/j.eswa.2019.112821. S2CID 199019309.
^ Gerla, G. (2016). «Комментарии к некоторым теориям нечетких вычислений». International Journal of General Systems . 45 (4): 372–392. Bibcode : 2016IJGS...45..372G. doi : 10.1080/03081079.2015.1076403. S2CID 22577357.
^ "Lotfi Zadeh Berkeley". Архивировано из оригинала 11 февраля 2017 года.
^ Mares, Milan (2006). "Нечеткие множества". Scholarpedia . 1 (10): 2031. Bibcode : 2006SchpJ...1.2031M. doi : 10.4249/scholarpedia.2031 .
^ Коско, Барт . «Нечеткость против вероятности» (PDF) . Университет Южной Калифорнии. Архивировано (PDF) из оригинала 2 сентября 2006 г. Получено 9 ноября 2018 г.
^ Новак, В (2005). «Являются ли нечеткие множества разумным инструментом для моделирования неопределенных явлений?». Нечеткие множества и системы . 156 (3): 341–348. doi :10.1016/j.fss.2005.05.029.
^ Вэлиант, Лесли (2013). Вероятно, приблизительно правильно: алгоритмы природы для обучения и процветания в сложном мире . Нью-Йорк: Basic Books. ISBN 978-0465032716.
^ Ричардсон, Марк (2010). "6.863 Final Project Writeup" (PDF) . Архивировано (PDF) из оригинала 4 октября 2015 г. . Получено 2 октября 2015 г. .
^ Вери, Франческо (2017). «Нечеткие множественные атрибутивные условия в fsQCA: проблемы и решения». Социологические методы и исследования . 49 (2): 312–355. doi :10.1177/0049124117729693. S2CID 125146607.
^ Монтеро, Хесус Сехас (2011). «Компенсаторная нечеткая логика». Ingeniería Industrial (на испанском языке). 32 (2): 157–162. Гейл А304726398.
^ Акампора, Джованни; Ди Стефано, Бруно; Витиелло, Аутилия (ноябрь 2016 г.). «IEEE 1855™: Первый стандарт IEEE, спонсируемый Обществом вычислительного интеллекта IEEE [Society Briefs]». Журнал вычислительного интеллекта IEEE . 11 (4): 4–6. doi :10.1109/MCI.2016.2602068.
^ Ди Стефано, Бруно Н. (2013). «О необходимости стандартного языка для проектирования нечетких систем». О силе языка нечеткой разметки . Исследования по нечеткости и мягким вычислениям. Том 296. С. 3–15. doi :10.1007/978-3-642-35488-5_1. ISBN 978-3-642-35487-8.
^ О силе языка нечеткой разметки . Исследования по нечеткости и мягким вычислениям. Том 296. 2013. doi :10.1007/978-3-642-35488-5. ISBN 978-3-642-35487-8.

Библиография

Arabacioglu, BC (2010). «Использование системы нечеткого вывода для анализа архитектурного пространства». Applied Soft Computing . 10 (3): 926–937. doi :10.1016/j.asoc.2009.10.011.
Biacino, Loredana; Gerla, Giangiacomo (1 октября 2002 г.). «Нечеткая логика, непрерывность и эффективность». Архив для Mathematical Logic . 41 (7): 643–667. CiteSeerX 10.1.1.2.8029 . doi :10.1007/s001530100128. S2CID 12513452.
Кокс, Эрл (1994). Справочник по нечетким системам: практическое руководство по созданию, использованию и обслуживанию нечетких систем . Бостон: AP Professional. ISBN 978-0-12-194270-0.
Gerla, Giangiacomo (март 2006 г.). «Эффективность и многозначные логики». Journal of Symbolic Logic . 71 (1): 137–162. doi :10.2178/jsl/1140641166. S2CID 12322009.
Гаек, Петр (1998). Метаматематика нечеткой логики . Дордрехт: Клювер. ISBN 978-0-7923-5238-9.
Hájek, Petr (август 1995). "Нечеткая логика и арифметическая иерархия". Fuzzy Sets and Systems . 73 (3): 359–363. doi :10.1016/0165-0114(94)00299-M.
Халперн, Джозеф Ю. (2003). Рассуждения о неопределенности . Кембридж, Массачусетс: MIT Press . ISBN 978-0-262-08320-1.
Höppner, Frank; Klawonn, F.; Kruse, R .; Runkler, T. (1999). Нечеткий кластерный анализ: методы классификации, анализа данных и распознавания изображений . Нью-Йорк: John Wiley. ISBN 978-0-471-98864-9.
Ибрагим, Ахмад М. (1997). Введение в прикладную нечеткую электронику . Энглвуд Клиффс, Нью-Джерси: Prentice Hall . ISBN 978-0-13-206400-2.
Клир, Джордж Йиржи ; Фолгер, Тина А. (1988). Нечеткие множества, неопределенность и информация. Энглвуд Клиффс, Нью-Джерси: Prentice Hall . ISBN 978-0-13-345984-5.
Клир, Джордж Йиржи ; Сент-Клер, Уте Х.; Юань, Бо (1997). Теория нечетких множеств: основы и приложения . Энглвуд Клиффс, Нью-Джерси: Prentice Hall . ISBN 978-0-13-341058-7.
Клир, Джордж Йиржи ; Юань, Бо (1995). Нечеткие множества и нечеткая логика: теория и приложения . Аппер Сэддл Ривер, Нью-Джерси: Prentice Hall PTR . ISBN 978-0-13-101171-7.
Коско, Барт (1993). Нечеткое мышление: новая наука нечеткой логики. Нью-Йорк: Hyperion. ISBN 978-0-7868-8021-8.
Коско, Барт; Исака, Сатору (июль 1993 г.). «Нечеткая логика». Scientific American . 269 (1): 76–81. Bibcode : 1993SciAm.269a..76K. doi : 10.1038/scientificamerican0793-76.
Лохани, АК; Гоэль, НК; Бхатия, ККС (2006). «Система нечеткого вывода Такаги–Сугено для моделирования взаимосвязи уровня и расхода». Журнал гидрологии . 331 (1): 146–160. Bibcode : 2006JHyd..331..146L. doi : 10.1016/j.jhydrol.2006.05.007.
Лохани, АК; Гоэль, НК; Бхатия, ККС (2007). «Выведение соотношений уровень–расход–концентрация осадков с использованием нечеткой логики». Журнал гидрологических наук . 52 (4): 793–807. Bibcode : 2007HydSJ..52..793L. doi : 10.1623/hysj.52.4.793. S2CID 117782707.
Лохани, АК; Гоэль, НК; Бхатия, ККС (2012). «Моделирование гидрологических временных рядов: сравнение адаптивных нейро-нечетких, нейронных сетей и авторегрессионных методов». Журнал гидрологии . 442–443 (6): 23–35. Bibcode : 2012JHyd..442...23L. doi : 10.1016/j.jhydrol.2012.03.031.
Масмуди, Малек; Хаит, Ален (ноябрь 2012 г.). "Моделирование нечеткой неопределенности для планирования проектов; применение к обслуживанию вертолетов" (PDF) . Международный журнал исследований производства . 50 (24). Архивировано (PDF) из оригинала 22 сентября 2017 г.
Мериго, Хосе М.; Хиль-Лафуэнте, Анна М.; Ягер, Рональд Р. (февраль 2015 г.). «Обзор нечетких исследований с библиометрическими показателями». Applied Soft Computing . 27 : 420–433. doi :10.1016/j.asoc.2014.10.035.
Миронов, AM (август 2005). "Нечеткие модальные логики". Журнал математических наук . 128 (6): 3461–3483. doi : 10.1007/s10958-005-0281-1 . S2CID 120674564.
Монтанья, Франко (2001). «Три задачи сложности в количественной нечеткой логике». Студия Логика . 68 (1): 143–152. дои : 10.1023/А: 1011958407631. S2CID 20035297.
Мундичи, Даниэле; Чиньоли, Роберто; Д'Оттавиано, Итала МЛ (1999). Алгебраические основы многозначных рассуждений . Дордрехт: Клювер Академик. ISBN 978-0-7923-6009-4.
Новак, Вилем (1989). Нечеткие множества и их приложения . Бристоль: Адам Хильгер. ISBN 978-0-85274-583-0.
Новак, Вилем (2005). «О теории нечетких типов». Нечеткие множества и системы . 149 (2): 235–273. дои : 10.1016/j.fss.2004.03.027.
Новак, Вилем; Перфильева Ирина; Мочкорж, Иржи (1999). Математические принципы нечеткой логики . Дордрехт: Клювер Академик. ISBN 978-0-7923-8595-0.
Онсес, Ричард (1996). Эксперт второго порядка: новый инструмент для изменения парадигм в расчете странового риска . Universidad, Secretariado de Publicaciones. ISBN 978-84-7719-558-0.
Онсес, Ричард (1994). Определение неопределенности, присущей инвестициям в латинской Америке, на основе теории наших ансамблей . Барселона. ISBN 978-84-475-0881-5.{{cite book}}: CS1 maint: location missing publisher (link)
Пассино, Кевин М.; Юркович, Стивен (1998). Нечеткое управление. Бостон: Addison-Wesley . ISBN 978-0-201-18074-9.
Педриц, Витольд; Гомид, Фернандо (2007). Нечеткая системная инженерия: к человеко-ориентированным вычислениям . Хобокен: Wiley-Interscience . ISBN 978-0-471-78857-7.
Пао-Мин, Пу ; Ин-Мин, Лю (август 1980 г.). «Нечеткая топология. I. Структура соседства нечеткой точки и сходимость Мура-Смита». Журнал математического анализа и приложений . 76 (2): 571–599. doi : 10.1016/0022-247X(80)90048-7 .
Sahoo, Bhabagrahi; Lohani, AK; Sahu, Rohit K. (2006). "Нечеткие многоцелевые и линейные программные модели управления для оптимального планирования системы земля-вода-урожаи". Water Resources Management . 20 (6): 931–948. Bibcode : 2006WatRM..20..931S. doi : 10.1007/s11269-005-9015-x. S2CID 154264034.
Сантос, Юджин С. (1970). «Нечеткие алгоритмы». Информация и управление . 17 (4): 326–339. doi : 10.1016/S0019-9958(70)80032-8 .
Скарпеллини, Бруно (июнь 1962 г.). «Die nichtaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz». Журнал символической логики . 27 (2): 159–170. дои : 10.2307/2964111. hdl : 20.500.11850/423097 . JSTOR 2964111. S2CID 26330059.
Seising, Rudolf (2007). Нечеткая детализация систем. Генезис теории нечетких множеств и ее начальные приложения — разработки до 1970-х годов . Springer-Verlag. ISBN 978-3-540-71795-9.
Steeb, Willi-Hans (2008). Нелинейная рабочая тетрадь: хаос, фракталы, клеточные автоматы, нейронные сети, генетические алгоритмы, программирование экспрессии генов, машина опорных векторов, вейвлеты, скрытые марковские модели, нечеткая логика с программами на C++, Java и SymbolicC++ (4-е изд.). World Scientific. ISBN 978-981-281-852-2.
Цитоловский, Лев; Сандлер, Узиэль (2008). Neural Cell Behavior and Fuzzy Logic . Springer. ISBN 978-0-387-09542-4.
Видерманн, Дж. (2004). «Характеристика супертьюринговой вычислительной мощности и эффективности классических нечетких машин Тьюринга». Теоретическая информатика . 317 (1–3): 61–69. doi : 10.1016/j.tcs.2003.12.004 .
Ягер, Рональд Р.; Филев, Димитар П. (1994). Основы нечеткого моделирования и управления . Нью-Йорк: Wiley. ISBN 978-0-471-01761-5.
Ван Пелт, Майлз (2008). Нечеткая логика в применении к повседневной жизни . Сиэтл, Вашингтон: Нет Нет Нет Нет Пресс. ISBN 978-0-252-16341-8.
Фон Альтрок, Константин (1995). Объяснение нечеткой логики и приложений NeuroFuzzy . Upper Saddle River, NJ: Prentice Hall PTR. ISBN 978-0-13-368465-0.
Уилкинсон, Р. Х. (1963). «Метод генерации функций нескольких переменных с использованием аналоговой диодной логики». Труды IEEE по электронным компьютерам . 12 (2): 112–129. doi :10.1109/PGEC.1963.263419.
Заде, LA (февраль 1968). «Нечеткие алгоритмы». Информация и управление . 12 (2): 94–102. doi : 10.1016/S0019-9958(68)90211-8 .
Заде, LA (июнь 1965). «Нечеткие множества». Информация и управление . 8 (3). Сан-Диего: 338–353. doi : 10.1016/S0019-9958(65)90241-X . ISSN 0019-9958. Zbl 0139.24606. Wikidata Q25938993.
Зайцев, ДА; Сарбей, ВГ; Слепцов, АИ (1998). «Синтез функций непрерывной логики, заданных в табличной форме». Кибернетика и системный анализ . 34 (2): 190–195. doi :10.1007/BF02742068. S2CID 120220846.
Циммерман, Х. (2001). Теория нечетких множеств и ее приложения . Бостон: Kluwer Academic Publishers . ISBN 978-0-7923-7435-0.

Внешние ссылки

IEC 1131-7 CD1 Архивировано 04.03.2021 на Wayback Machine IEC 1131-7 CD1 PDF
Нечеткая логика – статья в Scholarpedia
Моделирование с помощью слов – статья на Scholarpedia
Нечеткая логика – статья в Стэнфордской энциклопедии философии
Нечеткая математика – Введение в нечеткую логику для начинающих
Нечеткость и точность – Нечеткость в повседневной жизни, науке, религии, этике, политике и т. д.
Fuzzylite – кроссплатформенная, бесплатная библиотека управления нечеткой логикой с открытым исходным кодом, написанная на C++. Также имеет очень полезный графический пользовательский интерфейс в QT4.
Более гибкое машинное обучение – Массачусетский технологический институт описывает одно из приложений.
Семантическое сходство. Архивировано 4 октября 2015 г. на Wayback Machine. Массачусетский технологический институт предоставляет подробную информацию о нечетком семантическом сходстве.