

В математике единичная окружность — это окружность единичного радиуса , то есть радиуса 1. [1] Часто, особенно в тригонометрии , единичная окружность — это окружность радиуса 1 с центром в начале координат (0, 0) в декартовой системе координат на евклидовой плоскости . В топологии ее часто обозначают как S 1 , поскольку она представляет собой одномерную единичную n -сферу . [2] [примечание 1]
Если ( x , y ) — точка на окружности единичного круга , то | x | и | y | — длины катетов прямоугольного треугольника , гипотенуза которого имеет длину 1. Таким образом, по теореме Пифагора , x и y удовлетворяют уравнению
Поскольку x 2 = (− x ) 2 для всех x , и поскольку отражение любой точки единичной окружности относительно оси x или y также находится на единичной окружности, приведенное выше уравнение справедливо для всех точек ( x , y ) единичной окружности, а не только для тех, которые находятся в первом квадранте.
Внутренняя часть единичного круга называется открытым единичным кругом , тогда как внутренняя часть единичного круга, объединенная с самим единичным кругом, называется замкнутым единичным кругом.
Можно также использовать другие понятия «расстояния» для определения других «единичных окружностей», таких как окружность Римана ; дополнительные примеры см. в статье о математических нормах .

В комплексной плоскости числа единичной величины называются единичными комплексными числами . Это множество комплексных чисел z таких, что При разложении на действительную и мнимую составляющие это условие имеет вид
Комплексную единичную окружность можно параметризовать с помощью угловой меры относительно положительной действительной оси , используя комплексную показательную функцию (см. формулу Эйлера ).
При выполнении операции комплексного умножения единичные комплексные числа образуют группу , называемую группой окружности , обычно обозначаемую В квантовой механике единичное комплексное число называется фазовым множителем .

Тригонометрические функции косинуса и синуса угла θ можно определить на единичной окружности следующим образом: если ( x , y ) — точка на единичной окружности, и если луч из начала координат (0, 0) в ( x , y ) образует угол θ с положительной осью x (где поворот против часовой стрелки положителен), то
Уравнение x 2 + y 2 = 1 дает соотношение
Единичная окружность также демонстрирует, что синус и косинус являются периодическими функциями , причем тождества выполняются для любого целого числа k .
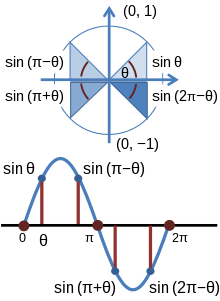
Треугольники, построенные на единичной окружности, также можно использовать для иллюстрации периодичности тригонометрических функций. Сначала построим радиус OP из начала координат O в точку P( x 1 , y 1 ) на единичной окружности так, чтобы угол t с 0 < t < π/2 образован положительным плечом оси x . Теперь рассмотрим точку Q( x 1 ,0) и отрезки PQ ⊥ OQ . Результатом является прямоугольный треугольник △OPQ с ∠QOP = t . Поскольку PQ имеет длину y 1 , OQ длину x 1 , а OP имеет длину 1 как радиус на единичной окружности, sin( t ) = y 1 и cos( t ) = x 1 . Установив эти эквивалентности, возьмем другой радиус OR из начала координат в точку R(− x 1 , y 1 ) на окружности так, чтобы тот же угол t был образован с отрицательным плечом оси x . Теперь рассмотрим точку S(− x 1 ,0) и отрезки RS ⊥ OS . Результатом является прямоугольный треугольник △ORS с ∠SOR = t . Отсюда можно видеть, что, поскольку ∠ROQ = π − t , R находится в точке (cos(π − t ), sin(π − t )) таким же образом, как P находится в точке (cos( t ), sin( t )) . Вывод состоит в том, что, поскольку (− x 1 , y 1 ) то же самое, что и (cos(π − t ), sin(π − t )) и ( x 1 , y 1 ) то же самое, что и (cos( t ),sin( t )) , верно, что sin( t ) = sin(π − t ) и −cos( t ) = cos(π − t ) . Аналогичным образом можно сделать вывод, что tan(π − t ) = −tan( t ) , поскольку tan( t ) = г 1/х 1 и тангенс(π − t ) = г 1/− х 1 . Простую демонстрацию вышесказанного можно увидеть в равенстве sin( π/4 ) = sin( 3π/4 ) = 1/√ 2 .
При работе с прямоугольными треугольниками синус, косинус и другие тригонометрические функции имеют смысл только для угловых мер больше нуля и меньше π/2 . Однако, будучи определенными с единичной окружностью, эти функции производят значимые значения для любой действительной угловой меры – даже большей, чем 2π . Фактически, все шесть стандартных тригонометрических функций – синус, косинус, тангенс, котангенс, секанс и косеканс, а также архаичные функции, такие как версинус и экссеканс – могут быть определены геометрически в терминах единичной окружности, как показано справа.
Используя единичную окружность, значения любой тригонометрической функции для многих углов, отличных от отмеченных, можно легко вычислить вручную, используя формулы суммы и разности углов .


Множество Жюлиа дискретной нелинейной динамической системы с функцией эволюции : представляет собой единичную окружность. Это простейший случай, поэтому он широко используется при изучении динамических систем.