Звездный параллакс

Понятие в астрономии

Звездный параллакс является основой парсека , который представляет собой расстояние от Солнца до астрономического объекта , имеющего угол параллакса в одну угловую секунду . (1 а.е. и 1 парсек не в масштабе, 1 парсек = ~206265 а.е.)

Звездный параллакс — это кажущееся смещение положения ( параллакс ) любой близлежащей звезды (или другого объекта) на фоне далеких звезд. В более широком смысле, это метод определения расстояния до звезды с помощью тригонометрии, метод звездного параллакса . Созданный различными орбитальными положениями Земли , чрезвычайно малый наблюдаемый сдвиг является наибольшим в интервалах времени около шести месяцев, когда Земля достигает противоположных сторон Солнца на своей орбите, давая базовое расстояние около двух астрономических единиц между наблюдениями. Сам параллакс считается половиной этого максимума, примерно эквивалентным наблюдаемому сдвигу, который произошел бы из-за различных положений Земли и Солнца, базовой линии в одну астрономическую единицу (а.е.).

Звездный параллакс настолько трудно обнаружить, что его существование было предметом многочисленных споров в астрономии на протяжении сотен лет. Томас Хендерсон , Фридрих Георг Вильгельм фон Струве и Фридрих Бессель провели первые успешные измерения параллакса в 1832–1838 годах для звезд Альфа Центавра , Вега и 61 Лебедя .

История измерений

Ранняя теория и попытки

Гелиометр Доллонда конца 1700-х годов

Звездный параллакс настолько мал, что был ненаблюдаем до 19 века, и его кажущееся отсутствие использовалось в качестве научного аргумента против гелиоцентризма в раннюю современную эпоху . Из геометрии Евклида ясно , что эффект был бы незаметен, если бы звезды находились достаточно далеко, но по разным причинам такие гигантские расстояния казались совершенно неправдоподобными: одним из главных возражений Тихо Браге против гелиоцентризма Коперника было то, что для того, чтобы он был совместим с отсутствием наблюдаемого звездного параллакса, между орбитой Сатурна и восьмой сферой (неподвижными звездами) должна была бы быть огромная и маловероятная пустота. ^[1]

Джеймс Брэдли впервые попытался измерить звездные параллаксы в 1729 году. Движение звезд оказалось слишком незначительным для его телескопа , но вместо этого он открыл аберрацию света ^[2] и нутацию земной оси и каталогизировал 3222 звезды.

19-й и 20-й века

Гелиометр Бесселя

Разрезная линза Бамбергского гелиометра (конец XIX века)

Измерение годового параллакса было первым надежным способом определения расстояний до ближайших звезд. Во второй четверти XIX века технический прогресс достиг уровня, который обеспечивал достаточную точность и правильность для измерений звездного параллакса. Джузеппе Каландрелли заметил звездный параллакс в 1805-6 годах и вывел 4-секундное значение для звезды Вега , что было сильно завышено. ^[3] Первые успешные измерения звездного параллакса были выполнены Томасом Хендерсоном в Кейптауне, Южная Африка , в 1832–1833 годах, где он измерил параллакс одной из ближайших звезд, Альфы Центавра . ^{[4] [5]} Между 1835 и 1836 годами астроном Фридрих Георг Вильгельм фон Струве в обсерватории Дерптского университета измерил расстояние до Веги и опубликовал свои результаты в 1837 году. ^[6] Фридрих Бессель , друг Струве, в 1837–1838 годах провел интенсивную наблюдательную кампанию в Кенигсбергской обсерватории за звездой 61 Лебедя , используя гелиометр , и опубликовал свои результаты в 1838 году. ^{[7] [8]} Хендерсон опубликовал свои результаты в 1839 году, после возвращения из Южной Африки.

Эти три результата, два из которых были измерены с помощью лучших на тот момент инструментов (большого рефрактора Фраунгофера, использовавшегося Струве, и гелиометра Фраунгофера Бесселя), были первыми в истории, установившими надежную шкалу расстояний до звезд. ^[9]

Большой гелиометр был установлен в обсерватории Куффнера (Вена) в 1896 году и использовался для измерения расстояний до других звезд с помощью тригонометрического параллакса. ^[10] К 1910 году он вычислил 16 расстояний параллакса до других звезд из всего лишь 108 известных науке на тот момент. ^[10]

Схема гелиометра из Британской энциклопедии 1911 года , которая представляет собой вид на разделенную линзу гелиометра.

Поскольку их было очень трудно измерить, к концу XIX века удалось получить всего около 60 звездных параллаксов, в основном с помощью нитяного микрометра . Астрографы, использующие астрономические фотопластинки , ускорили процесс в начале XX века. Автоматизированные машины для измерения пластинок ^[11] и более сложные компьютерные технологии 1960-х годов позволили более эффективно составлять звездные каталоги . В 1980-х годах приборы с зарядовой связью (ПЗС) заменили фотографические пластинки и снизили оптическую неопределенность до одной угловой миллисекунды. ^{[ необходима цитата ]}

Звездный параллакс остается стандартом для калибровки других методов измерения (см. Космическая лестница расстояний ). Точные расчеты расстояния на основе звездного параллакса требуют измерения расстояния от Земли до Солнца, которое теперь известно с исключительной точностью на основе отражения радара от поверхностей планет. ^[12]

Космическая астрометрия

Точность измерения расстояний до звезд с помощью телескопа Хаббл была увеличена в 10 раз вглубь Млечного Пути . ^[13]

В 1989 году спутник Hipparcos был запущен в первую очередь для получения параллаксов и собственных движений близлежащих звезд, увеличив количество звездных параллаксов, измеренных с точностью до миллисекунды дуги, в тысячу раз. Тем не менее, Hipparcos способен измерять углы параллакса только для звезд, находящихся на расстоянии до 1600 световых лет , что составляет чуть больше одного процента от диаметра Галактики Млечный Путь .

Телескоп Хаббла WFC3 теперь имеет точность от 20 до 40 микросекунд дуги, что позволяет проводить надежные измерения расстояний до 3066 парсеков (10 000 световых лет) для небольшого числа звезд. ^[14] Это повышает точность космической лестницы расстояний и улучшает знание расстояний во Вселенной на основе размеров орбиты Земли.

По мере увеличения расстояния между двумя точками наблюдения визуальный эффект параллакса также становится более заметным. Космический аппарат NASA New Horizons выполнил первое измерение межзвездного параллакса 22 апреля 2020 года, сделав снимки Проксимы Центавра и Вольфа 359 совместно с наземными обсерваториями. Относительная близость двух звезд в сочетании с расстоянием космического аппарата от Земли в 6,5 миллиардов километров (около 43 а.е.) дала различимый параллакс в угловые минуты, что позволило визуально увидеть параллакс без инструментов. ^[15]

Параллакс Проксимы Центавра, наблюдаемый с New Horizons и Земли. ^[16]

Ожидается, что миссия Gaia Европейского космического агентства , запущенная 19 декабря 2013 года, будет измерять углы параллакса с точностью до 10 микросекунд дуги для всех умеренно ярких звезд, тем самым картографируя близлежащие звезды (и потенциально планеты) на расстоянии до десятков тысяч световых лет от Земли. ^[17] В выпуске данных 2 в 2018 году заявлены средние ошибки для параллаксов 15-й величины и более ярких звезд в 20–40 микросекунд дуги. ^[18]

Радиоастрометрия

Интерферометрия с очень длинной базой в радиодиапазоне может создавать изображения с угловым разрешением около 1 угловой миллисекунды, и, следовательно, для ярких радиоисточников точность измерений параллакса, выполненных в радиодиапазоне, может легко превзойти ^{[ сомнительно – обсудить ]} точность оптических телескопов, таких как Gaia. Эти измерения, как правило, ограничены чувствительностью и должны проводиться по одному за раз, поэтому работа обычно выполняется только для таких источников, как пульсары и рентгеновские двойные, где радиоизлучение сильно по сравнению с оптическим излучением. ^{[ требуется цитата ]}

Метод параллакса

Принцип

В течение года отмечается положение звезды S по отношению к другим звездам в ее видимом окружении:

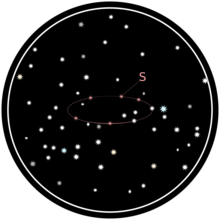
Звезды, которые, по-видимому, не двигаются относительно друг друга, используются в качестве опорных точек для определения пути S.

Наблюдаемый путь представляет собой эллипс: проекцию орбиты Земли вокруг Солнца через S на далекий фон неподвижных звезд. Чем дальше S удалена от оси орбиты Земли, тем больше эксцентриситет пути S. Центр эллипса соответствует точке, в которой S будет видна с Солнца:

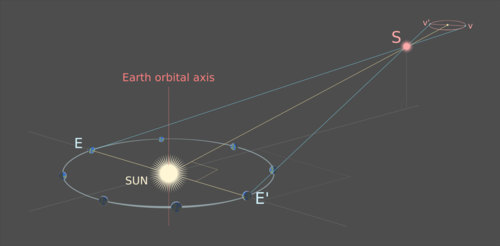
Плоскость орбиты Земли расположена под углом к ​​линии, проходящей через Солнце и S. Вершины v и v' эллиптической проекции траектории S являются проекциями положений Земли E и E ′, такими, что линия EE ′ пересекает линию Солнце-S под прямым углом; треугольник, образованный точками E, E ′ и S, является равнобедренным треугольником с линией Солнце-S в качестве оси симметрии.

Любые звезды, которые не перемещались между наблюдениями, с точки зрения точности измерения являются бесконечно далекими. Это означает, что расстояние движения Земли по сравнению с расстоянием до этих бесконечно далеких звезд составляет, с точки зрения точности измерения, 0. Таким образом, линия визирования от первой позиции Земли E до вершины v будет по сути такой же, как линия визирования от второй позиции Земли E ′ до той же вершины v, и, следовательно, будет проходить параллельно ей — невозможно убедительно изобразить на изображении ограниченного размера:

Так как прямая E ′ -v ′ является трансверсалью в той же (приблизительно евклидовой) плоскости, что и параллельные прямые Ev и E ′ -v, то отсюда следует, что соответствующие углы пересечения этих параллельных прямых с этой трансверсалью равны: угол θ между линиями зрения Ev и E ′ -v ′ равен углу θ между E ′ -v и E ′ -v ′ , который является углом θ между наблюдаемыми положениями S по отношению к его, по-видимому, неподвижному звездному окружению.

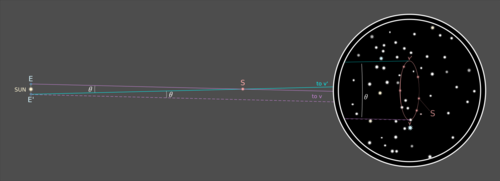
Расстояние d от Солнца до S теперь следует из простой тригонометрии:

 загар( ⁠1/2⁠ θ) = E-Sun / d,

так что d = E-Sun / tan( ⁠1/2⁠ θ), где E-Sun составляет 1 а.е.

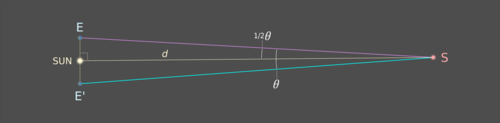
Чем дальше находится объект, тем меньше его параллакс.

Меры звездного параллакса даются в крошечных единицах угловых секунд или даже в тысячных долях угловых секунд (миллисекундах). Единица расстояния парсек определяется как длина катета прямоугольного треугольника, прилегающего к углу в одну угловую секунду в одной вершине , где другой катет имеет длину 1 а.е. Поскольку звездные параллаксы и расстояния все включают такие тонкие прямоугольные треугольники , можно использовать удобное тригонометрическое приближение для преобразования параллаксов (в угловых секундах) в расстояние (в парсеках). Приблизительное расстояние является просто обратной величиной параллакса: например, Проксима Центавра (ближайшая к Земле звезда, кроме Солнца), параллакс которой равен 0,7685, находится на расстоянии 1 / 0,7685 парсека = 1,301 парсека (4,24 световых лет). ^[19] ${\displaystyle d{\text{ (pc)}}\approx 1/p{\text{ (arcsec)}}.}$

Варианты

Звездный параллакс чаще всего измеряется с помощью годового параллакса , определяемого как разница в положении звезды, видимой с Земли и Солнца, т. е. угол, образуемый звездой средним радиусом орбиты Земли вокруг Солнца. Парсек ( 3,26 светового года ) определяется как расстояние, для которого годовой параллакс составляет 1  угловую секунду . Годовой параллакс обычно измеряется путем наблюдения за положением звезды в разное время года по мере движения Земли по своей орбите.

Углы, используемые в этих вычислениях, очень малы и поэтому их трудно измерить. Ближайшая к Солнцу звезда (а также звезда с самым большим параллаксом), Проксима Центавра , имеет параллакс 0,7685 ± 0,0002 угловых секунд. ^[19] Этот угол приблизительно равен углу, образуемому объектом диаметром 2 сантиметра, находящимся на расстоянии 5,3 километра.

Вывод

Для прямоугольного треугольника ,

${\displaystyle \tan p={\frac {1\,{\text{au}}}{d}},}$

где — параллакс, 1 а.е. (149 600 000 км) — приблизительное среднее расстояние от Солнца до Земли, а — расстояние до звезды. Используя приближения малых углов (справедливые, когда угол мал по сравнению с 1 радианом ), ${\displaystyle p}$ ${\displaystyle d}$

${\displaystyle \tan x\approx x{\text{ radians}}=x\cdot {\frac {180}{\pi }}{\text{ degrees}}=x\cdot 180\cdot {\frac {3600}{\pi }}{\text{ arcseconds}},}$

поэтому параллакс, измеряемый в угловых секундах, равен

${\displaystyle p''\approx {\frac {1{\text{ au}}}{d}}\cdot 180\cdot {\frac {3600}{\pi }}.}$

Если параллакс равен 1", то расстояние равно

${\displaystyle d=1{\text{ au}}\cdot 180\cdot {\frac {3600}{\pi }}\approx 206,265{\text{ au}}\approx 3.2616{\text{ ly}}\equiv 1{\text{ parsec}}.}$

Это определяет парсек , удобную единицу измерения расстояния с использованием параллакса. Таким образом, расстояние, измеренное в парсеках, просто равно , когда параллакс дан в угловых секундах. ^[20] ${\displaystyle d=1/p}$

Ошибка

Точные измерения расстояния параллакса имеют связанную ошибку. Эта ошибка в измеренном угле параллакса не переводится напрямую в ошибку расстояния, за исключением относительно небольших ошибок. Причина этого в том, что ошибка в сторону меньшего угла приводит к большей ошибке расстояния, чем ошибка в сторону большего угла.

Однако приближенную погрешность расстояния можно вычислить следующим образом:

${\displaystyle \delta d=\delta \left({1 \over p}\right)=\left|{\partial \over \partial p}\left({1 \over p}\right)\right|\delta p={\delta p \over p^{2}}}$

где d — расстояние, а p — параллакс. Приближение гораздо точнее для ошибок параллакса, которые малы относительно параллакса, чем для относительно больших ошибок. Для значимых результатов в звездной астрономии голландский астроном Флор ван Леувен рекомендует, чтобы ошибка параллакса не превышала 10% от общего параллакса при вычислении этой оценки ошибки. ^[21]

Смотрите также

• Видимое место
• ТАУ (космический корабль) (заброшенный проект космической миссии, в котором использовался бы параллакс)

Ссылки

1. См. стр. 51 в The perception of Copernicus' heliocentric theory: materials of a symposium organization by the Nicolas Copernicus Committee of the International Union of the History and Philosophy of Science , Torun, Poland, 1973, ed. Jerzy Dobrzycki, International Union of the History and Philosophy of Science. Nicolas Copernicus Committee; ISBN  90-277-0311-6 , ISBN 978-90-277-0311-8 
2. Буххайм, Роберт (4 октября 2007 г.). Небо — твоя лаборатория. Springer. ISBN 978-0-387-73995-3.Страница 184.
3. Гор, Дж. Э. (1904). Исследования по астрономии. Лондон: Chatto & Windus. стр. 42.
4. Хендерсон, Томас (1839). «О параллаксе α Центавра». Monthly Notices of the Royal Astronomical Society . 4 (19): 168–170. Bibcode :1839MNRAS...4..168H. doi : 10.1093/mnras/4.19.168 .
5. Хендерсон, Томас (1840). «О параллаксе α Центавра». Мемуары Королевского астрономического общества . 11 : 61–68. Бибкод : 1840MmRAS..11...61H.
6. фон Струве, Фридрих Георг Вильгельм (1837). «Stellarum duplicium et multiplicium mensurae micrometricae per magnum Fraunhoferi Tubem Annis в 1824 г. по 1837 г. в зеркалах Dorpatensi institutae». Астрономические Нахрихтен . 14 (16): 249–252. Бибкод : 1837AN.....14..249S. дои : 10.1002/asna.18370141609.
7. Зейлик и Грегори 1998, стр. 44.
8. Бессель, Ф.В., "Bestimmung der Entfernung des 61sten Sterns des Schwans. Архивировано 24 июня 2007 г. в Wayback Machine " (1838) Astronomische Nachrichten , vol. 16, стр. 65–96.
9. Рид, Марк (2020). «Возвращение к первым звездным параллаксам». Астрономические Нахрихтен . 341 (9): 860–869. arXiv : 2009.11913 . Бибкод : 2020AN....341..860R. дои : 10.1002/asna.202013833. S2CID  221949223.
10. Хабисон, Питер (1998). «Астрометрия и ранняя астрофизика в обсерватории Каффнера в конце 19 века». Acta Historica Astronomiae . 3 : 93–94. Бибкод : 1998AcHA....3...93H. ISSN  0003-2670.
11. Бумага ЦЕРН на пластине измерительной машины USNO StarScan
12. Зейлик и Грегори 1998, § 22-3.
13. "Хаббл растягивает звездную рулетку в десять раз дальше". ESA/Hubble Images . Получено 12 апреля 2014 г.
14. Харрингтон, Дж. Д.; Виллар, Рэй (10 апреля 2014 г.). «NASA's Hubble Extends Stellar Tape Measure 10 Times Farther into Space» ( НАСА) . Получено 17 октября 2014 г.Рисс, Адам Г .; Казертано, Стефано; Андерсон, Джей; Маккенти, Джон; Филиппенко, Алексей В. (2014). «Параллакс за пределами килопарсека от пространственного сканирования широкоугольной камеры 3 на космическом телескопе Хаббла». The Astrophysical Journal . 785 (2): 161. arXiv : 1401.0484 . Bibcode : 2014ApJ...785..161R. doi : 10.1088/0004-637X/785/2/161. S2CID  55928992.
15. Талберт, Триша (10 июня 2020 г.). «New Horizons проводит первый межзвездный эксперимент по параллаксу». NASA . Архивировано из оригинала 4 ноября 2023 г. Получено 20 мая 2021 г.
16. Талберт, Триша (10 июля 2020 г.). «New Horizons проводит первый межзвездный эксперимент по параллаксу». NASA . Архивировано из оригинала 4 ноября 2023 г. Получено 14 июля 2020 г.
17. Хенни, Пол Дж. "Миссия ЕКА Gaia по изучению звезд". Astronomy Today . Получено 8 марта 2008 г.
18. Браун, AGA ; и др. (коллаборация Gaia) (август 2018 г.). "Gaia Data Release 2: Summary of the content and survey properties". Астрономия и астрофизика . 616 . A1. arXiv : 1804.09365 . Bibcode : 2018A&A...616A...1G . doi : 10.1051/0004-6361/201833051 .
19. Brown, AGA ; et al. (сотрудничество Gaia) (август 2018 г.). "Gaia Data Release 2: Summary of the content and survey properties". Astronomy & Astrophysics . 616 . A1. arXiv : 1804.09365 . Bibcode : 2018A&A...616A...1G . doi : 10.1051/0004-6361/201833051 .
20. Аналогичные выводы есть в большинстве учебников по астрономии. См., например, Zeilik & Gregory 1998, § 11-1.
21. van Leeuwen, Floor (2007). Hipparcos, новая редукция необработанных данных. Библиотека астрофизики и космической науки. Т. 350. Springer. С. 86. ISBN 978-1-4020-6341-1. Архивировано из оригинала 18 марта 2015 года.

• Хиршфельд, Алан В. (2001). Параллакс: гонка за измерение космоса . Нью-Йорк: WH Freeman. ISBN 0-7167-3711-6.
• Уиппл, Фред Л. (2007). Земля Луна и планеты . Читать книги. ISBN 978-1-4067-6413-0..
• Зейлик, Майкл А.; Грегори, Стефан А. (1998). Введение в астрономию и астрофизику (4-е изд.). Saunders College Publishing. ISBN 0-03-006228-4..

Дальнейшее чтение

• Дайсон, Ф. В. (1915). «Измерение расстояний до звезд». Обсерватория . 38 : 292. Bibcode : 1915Obs....38..292D.