Конструируемый многоугольник

Правильный многоугольник, который можно построить с помощью циркуля и линейки

Построение правильного пятиугольника

В математике конструктивный многоугольник — это правильный многоугольник , который можно построить с помощью циркуля и линейки . Например, правильный пятиугольник можно построить с помощью циркуля и линейки, а правильный семиугольник — нет. Существует бесконечно много конструктивных многоугольников, но известны только 31 с нечетным числом сторон.

Условия конструктивности

Число сторон известных конструируемых многоугольников, имеющих до 1000 сторон (жирный) или нечетное количество сторон (красный)

Строительство правильного 17-угольника

Некоторые правильные многоугольники легко построить с помощью циркуля и линейки, другие — нет. Древнегреческие математики знали, как построить правильный многоугольник с 3, 4 или 5 сторонами, ^{[1] : с. xi} , и они знали, как построить правильный многоугольник с удвоенным числом сторон заданного правильного многоугольника. ^{[1] : с. 49–50} Это привело к постановке вопроса: возможно ли построить все правильные многоугольники с помощью циркуля и линейки? Если нет, то какие n -угольники (то есть многоугольники с n ребрами) можно построить, а какие — нет?

Карл Фридрих Гаусс доказал конструктивность правильного 17-угольника в 1796 году. Пять лет спустя он разработал теорию гауссовых периодов в своих Disquisitiones Arithmeticae . Эта теория позволила ему сформулировать достаточное условие конструктивности правильных многоугольников. Гаусс утверждал без доказательства, что это условие также является необходимым , ^[2], но никогда не публиковал свое доказательство.

Полное доказательство необходимости было дано Пьером Ванцелем в 1837 году. Результат известен как теорема Гаусса–Ванцеля : правильный n -угольник может быть построен с помощью циркуля и линейки тогда и только тогда, когда n является произведением степени числа 2 и любого количества различных простых чисел Ферма . Здесь степень числа 2 — это число вида , где m ≥ 0 — целое число. Простое число Ферма — это простое число вида , где m ≥ 0 — целое число. Количество вовлеченных простых чисел Ферма может быть равно 0, и в этом случае n является степенью числа 2. ${\displaystyle 2^{m}}$ ${\displaystyle 2^{(2^{m})}+1}$

Чтобы свести геометрическую задачу к задаче чистой теории чисел , доказательство использует тот факт, что правильный n -угольник конструктивен тогда и только тогда, когда косинус является конструктивным числом , то есть может быть записан в терминах четырех основных арифметических операций и извлечения квадратных корней . Эквивалентно, правильный n -угольник конструктивен, если любой корень n -го циклотомического многочлена конструктивен. ${\displaystyle \cos(2\pi /n)}$

Подробные результаты теории Гаусса

Переформулируем теорему Гаусса–Ванцеля:

Правильный n -угольник можно построить с помощью линейки и циркуля тогда и только тогда, когда n = 2 ^k p ₁ p ₂ ... p _t , где k и t — неотрицательные целые числа , а числа p _i (когда t > 0) — различные простые числа Ферма.

Пять известных простых чисел Ферма :

F ₀ = 3, F ₁ = 5, F ₂ = 17, F ₃ = 257 и F ₄ = 65537 (последовательность A019434 в OEIS ).

Поскольку существует 31 непустое подмножество пяти известных простых чисел Ферма, существует 31 известный конструируемый многоугольник с нечетным числом сторон.

Известно , что следующие двадцать восемь чисел Ферма, от F ₅ до F ₃₂ , являются составными . ^[3]

Таким образом, правильный n -угольник можно построить, если

п = 3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 16 , 17 , 20 , 24 , 30 , 32 , 34 , 40 , 48 , 51, 60 , 64 , 68, 80 , 85, 96 , 102, 120 , 128, 136, 160, 170, 192, 204, 240, 255, 256, 257 , 272, 320, 340, 384, 408, 480, 510, 512, 514, 544, 640, 680, 768, 771, 816, 960, 1020, 1024, 1028, 1088, 1280, 1285, 1360, 1536, 1542, 1632, 1920, 2040, 2048, ... (последовательность A003401 в OEIS ),

в то время как правильный n -угольник невозможно построить с помощью циркуля и линейки, если

п = 7 , 9 , 11 , 13 , 14 , 18 , 19 , 21 , 22 , 23 , 25, 26 , 27, 28 , 29, 31, 33, 35, 36, 37, 38, 39, 41, 42 , 43, 44, 45, 46, 47, 49, 50 , 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 65, 66, 67, 69, 70 , 71, 72, 73, 74, 75, 76, 77, 78, 79, 81, 82, 83, 84, 86, 87, 88, 89, 90 , 91, 92, 93, 94, 95, 97, 98, 99, 100 , 101, 103, 104, 105, 106, 107, 108, 109, 110, 111, 112, 113, 114, 115, 116, 117, 118, 119, 121, 122, 123, 124, 125, 126, 127, ... (последовательность A004169 в OEIS ).

Связь с треугольником Паскаля

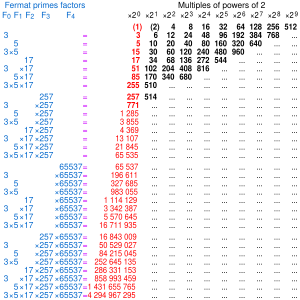
Поскольку известно пять простых чисел Ферма, нам известно 31 число, являющееся произведением различных простых чисел Ферма, и, следовательно, 31 конструируемый нечетносторонний правильный многоугольник. Это 3, 5, 15, 17, 51, 85, 255, 257, 771, 1285, 3855, 4369, 13107, 21845, 65535, 65537, 196611 , 327685, 983055, 1114129, 3342387, 5570645, 16711935, 16843009, 50529027, 84215045, 252645135, 286331153, 858993459, 1431655765, 4294967295 (последовательность A045544 в OEIS ). Как прокомментировал Джон Конвей в Книге чисел , эти числа, записанные в двоичном виде , равны первым 32 строкам треугольника Паскаля по модулю -2 за вычетом верхней строки, которая соответствует одноугольнику . (Из-за этого единицы в таком списке образуют приближение к треугольнику Серпинского .) После этого эта закономерность нарушается, поскольку следующее число Ферма является составным (4294967297 = 641 × 6700417), поэтому следующие строки не соответствуют конструктивным многоугольникам. Неизвестно, существуют ли еще простые числа Ферма, и поэтому неизвестно, сколько существует нечетных конструктивных правильных многоугольников. В общем случае, если существует q простых чисел Ферма, то существует 2 ^q −1 нечетных правильных конструктивных многоугольников.

Общая теория

В свете более поздних работ по теории Галуа принципы этих доказательств были прояснены. Из аналитической геометрии легко показать , что конструктивные длины должны происходить из базовых длин путем решения некоторой последовательности квадратных уравнений . ^[4] В терминах теории поля такие длины должны содержаться в расширении поля, порожденном башней квадратичных расширений . Из этого следует, что поле, порожденное конструкциями, всегда будет иметь степень над базовым полем, которая является степенью двойки.

В частном случае правильного n- угольника вопрос сводится к вопросу построения длины

потому что  ⁠2π​/н⁠ ,

которое является тригонометрическим числом и, следовательно, алгебраическим числом . Это число лежит в n -ом циклотомическом поле — и фактически в его действительном подполе , которое является полностью действительным полем и рациональным векторным пространством размерности

½ φ( n ),

где φ( n ) — функция Эйлера . Результат Ванцеля сводится к вычислению, показывающему, что φ( n ) является степенью 2 именно в указанных случаях.

Что касается построения Гаусса, то когда группа Галуа является 2-группой, то она имеет последовательность подгрупп порядков

1, 2, 4, 8, ...

которые вложены, каждое в следующее ( композиционный ряд , в терминологии теории групп ), что просто доказать индукцией в этом случае абелевой группы . Следовательно, существуют подполя, вложенные внутрь циклотомического поля, каждое из которых имеет степень 2 над предыдущим. Генераторы для каждого такого поля могут быть записаны с помощью гауссовой теории периодов . Например, для n  = 17 существует период, который является суммой восьми корней из единицы , один, который является суммой четырех корней из единицы, и один, который является суммой двух, что равно

потому что  ⁠2π​/17⁠ .

Каждое из них является корнем квадратного уравнения в терминах предыдущего. Более того, эти уравнения имеют действительные , а не комплексные корни, поэтому в принципе могут быть решены геометрическим построением: это потому, что вся работа происходит внутри полностью реального поля.

Таким образом, результат Гаусса можно понять в современных терминах; для фактического расчета решаемых уравнений периоды можно возвести в квадрат и сравнить с «нижними» периодами с помощью вполне осуществимого алгоритма.

Построение с помощью циркуля и линейки

Построения циркулем и линейкой известны для всех известных конструируемых многоугольников. Если n  =  pq с p  = 2 или p и q взаимно просты , n -угольник может быть построен из p -угольника и q -угольника.

• Если p  = 2, начертите q -угольник и разделите пополам один из его центральных углов. Из этого можно построить 2 q -угольник.
• Если p  > 2, впишите p -угольник и q -угольник в одну и ту же окружность таким образом, чтобы они имели общую вершину. Поскольку p и q взаимно просты, существуют целые числа a и b, такие что ap + bq = 1. Тогда 2 a π/ q + 2 b π/ p = 2π/ pq . Из этого можно построить pq -угольник.

Таким образом, нужно только найти конструкцию с помощью циркуля и линейки для n -угольников, где n — простое число Ферма.

• Построение равностороннего треугольника простое и известно с древности ; см. Равносторонний треугольник .
• Построения правильного пятиугольника были описаны как Евклидом ( Начала , ок. 300 г. до н. э.), так и Птолемеем ( Альмагест , ок. 150 г. н. э.).
• Хотя Гаусс доказал , что правильный 17-угольник можно построить, он фактически не показал , как это сделать. Первое построение принадлежит Эрчингеру, через несколько лет после работы Гаусса.
• Первые явные построения правильного 257-угольника были даны Магнусом Георгом Паукером (1822) ^[5] и Фридрихом Юлиусом Ришело (1832). ^[6]
• Построение правильного 65537-угольника впервые было дано Иоганном Густавом Гермесом (1894). Построение очень сложное; Гермес потратил 10 лет на завершение 200-страничной рукописи. ^[7]

Галерея

Слева направо, построения 15-угольника , 17-угольника , 257-угольника и 65537-угольника . Показан только первый этап построения 65537-угольника; построения 15-угольника, 17-угольника и 257-угольника приведены полностью.

Другие конструкции

Концепция конструктивности, обсуждаемая в этой статье, применяется конкретно к конструкциям с циркулем и линейкой . Больше конструкций становится возможным, если допускаются другие инструменты. Так называемые конструкции neusis , например, используют размеченную линейку. Построения являются математической идеализацией и предполагают, что они выполнены точно.

Правильный многоугольник с n сторонами может быть построен с помощью линейки, циркуля и трисектора углов тогда и только тогда, когда r, s, k ≥ 0 и где p _i являются различными простыми числами Пьерпонта, большими 3 (простыми числами вида ^{[8] : Теор. 2} Эти многоугольники являются в точности правильными многоугольниками, которые могут быть построены с помощью конического сечения , и правильными многоугольниками, которые могут быть построены с помощью складывания бумаги . Первые числа сторон этих многоугольников равны: ${\displaystyle n=2^{r}3^{s}p_{1}p_{2}\cdots p_{k},}$ ${\displaystyle 2^{t}3^{u}+1).}$

3, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 24, 26, 27, 28, 30, 32, 34, 35, 36, 37, 38, 39, 40, 42, 45, 48, 51, 52, 54, 56, 57, 60, 63, 64, 65, 68, 70, 72, 73, 74, 76, 78, 80, 81, 84, 85, 90, 91, 95, 96, 97, 102, 104, 105, 108, 109, 111, 112, 114, 117, 119, 120, 126, 128, 130, 133, 135, 136, 140, 144, 146, 148, 152, 153, 156, 160, 162, 3, 168, 170, 171, 180, 182, 185, 189, 190, 192, 193, 194, 195, 204, 208, 210, 216, 218, 219, 221, 222, 224, 228, 234, 238, 240, 243, 247, 252, 255, 256, 257, 259, 260, 266, 270, 272, 273, 280, 285, 288, 291, 292, 296, ... (последовательность A122254 в OEIS )

Смотрите также

• Полигон
• Карлайл круг

Ссылки

1. Bold, Benjamin. Знаменитые проблемы геометрии и способы их решения , Dover Publications, 1982 (ориг. 1969).
2. Гаусс, Карл Фридрих (1966). Disquisitiones arithmeticae. Нью-Хейвен и Лондон: Издательство Йельского университета. С. 458–460 . Получено 25 января 2023 г.
3. Простые множители k · 2n + 1 чисел Ферма Fm и полный статус факторизации Вильфрида Келлера.
4. Кокс, Дэвид А. (2012), "Теорема 10.1.6", Теория Галуа , Чистая и прикладная математика (2-е изд.), John Wiley & Sons, стр. 259, doi :10.1002/9781118218457, ISBN 978-1-118-07205-9.
5. Магнус Георг Паукер (1822). «Geometrische Verzeichnung des regelmäßigen Siebzehn-Ecks und Zweyhundersiebenundfünfzig-Ecks in den Kreis». Jahresverhandlungen der Kurländischen Gesellschaft für Literatur und Kunst (на немецком языке). 2 : 160–219.
6. Фридрих Юлиус Ришело (1832). «Desolvee алгебраическое уравнение x257 = 1, sive de Divisione circuli per bisectionem anguli septies repetitam in partes 257 inter se aequales commentatio coronata». Journal für die reine und angewandte Mathematik (на латыни). 9 : 1–26, 146–161, 209–230, 337–358. дои : 10.1515/crll.1832.9.337. S2CID  199545940.
7. Иоганн Густав Гермес (1894). «Über die Teilung des Kreises in 65537 gleiche Teile». Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (на немецком языке). 3 . Геттинген: 170–186.
8. Глисон, Эндрю М. (март 1988 г.). «Трисекция угла, семиугольник и трискайдекагон». American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624. JSTOR  2323624.

Внешние ссылки

• Duane W. DeTemple (1991). «Круги Карлейля и простота Лемуана многоугольных конструкций». The American Mathematical Monthly . 98 (2): 97–108. doi :10.2307/2323939. JSTOR  2323939. MR  1089454.
• Кристиан Готтлиб (1999). «Простая и понятная конструкция правильного 257-угольника». Mathematical Intelligencer . 21 (1): 31–37. doi :10.1007/BF03024829. MR  1665155. S2CID  123567824.
• Формулы правильных многоугольников, FAQ по запросу «Спросите доктора Математика».
• Карл Шик: Weiche Primzahlen und das 257-Eck: eine analytische Lösung des 257-Ecks. Цюрих: К. Шик, 2008. ISBN 978-3-9522917-1-9 . 
• 65537-угольник, точное построение первой стороны с использованием Квадратрикса Гиппия и GeoGebra в качестве дополнительных средств, с кратким описанием (на немецком языке)