Квадратное уравнение

Полиномиальное уравнение второй степени

В алгебре квадратное уравнение (от лат.quaratus  « квадрат » ) — это любое уравнение , которое можно преобразовать в стандартную форму как ^[1]

$${\displaystyle ax^{2}+bx+c=0\,,}$$

xнеизвестноеabca ≠ 0a = 0b ≠ 0линейноеabcкоэффициентамиквадратичным коэффициентомлинейным коэффициентомкоэффициентсвободный член^[2]

Значения x , удовлетворяющие уравнению, называются решениями уравнения, а корни или нули выражения — в его левой части. Квадратное уравнение имеет не более двух решений. Если существует только одно решение, говорят, что это двойной корень . Если все коэффициенты являются действительными числами , существует либо два действительных решения, либо один действительный двойной корень, либо два комплексных решения, которые являются комплексно-сопряженными друг другу. Квадратное уравнение всегда имеет два корня, если в него входят комплексные корни; а двойной корень считается за два. Квадратное уравнение можно разложить на эквивалентное уравнение ^[3]

$${\displaystyle ax^{2}+bx+c=a(x-r)(x-s)=0}$$

rsx

Квадратичная формула

$${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}}$$

abcЗаполнение квадрата

Решения задач, выражаемые с помощью квадратных уравнений, были известны еще в 2000 году до нашей эры. ^{[4] [5]}

Поскольку квадратное уравнение содержит только одну неизвестную, его называют « одномерным ». Квадратное уравнение содержит только степени x , которые являются неотрицательными целыми числами, и, следовательно, это полиномиальное уравнение . В частности, это полиномиальное уравнение второй степени , поскольку наибольшая степень равна двум.

Решение квадратного уравнения

Рисунок 1. Графики квадратичной функции y = ax ² + bx + c , варьирующей каждый коэффициент отдельно при фиксированных остальных коэффициентах (при значениях a  = 1, b  = 0, c  = 0)

Квадратное уравнение с действительными или комплексными коэффициентами имеет два решения, называемые корнями . Эти два решения могут быть разными, а могут и не быть разными, и они могут быть реальными, а могут и не быть.

Факторинг путем проверки

Квадратное уравнение ax ² + bx + c = 0 можно выразить как произведение ( px + q )( rx + s ) = 0 . В некоторых случаях можно путем простой проверки определить значения p , q , r и s , которые делают две формы эквивалентными друг другу. Если квадратное уравнение записано во второй форме, то «Свойство нулевого фактора» утверждает, что квадратное уравнение удовлетворяется, если px + q = 0 или rx + s = 0 . Решение этих двух линейных уравнений дает корни квадратного.

Для большинства учащихся факторизация методом проверки является первым методом решения квадратных уравнений, с которым они сталкиваются. ^{[6] : 202–207} Если дано квадратное уравнение в виде x ² + bx + c = 0 , искомая факторизация имеет вид ( x + q )( x + s ) , и нужно найти два числа q и s , которые в сумме дают b и произведение которых равно c (иногда это называют «правилом Виеты» ^[7] и связано с формулами Виеты ). Например, x ² + 5 x + 6 факторизуется как ( x + 3)( x + 2) . Более общий случай, когда a не равно 1, может потребовать значительных усилий в методе проб и ошибок, предполагая, что его вообще можно учесть путем проверки.

За исключением особых случаев, таких как b = 0 или c = 0 , факторизация методом проверки работает только для квадратных уравнений, имеющих рациональные корни. Это означает, что подавляющее большинство квадратных уравнений, возникающих в практических приложениях, не могут быть решены путем факторизации путем проверки. ^{[6] : 207}

Завершение площади

Рисунок 2. Для квадратичной функции y = x ² − x − 2 точки, в которых график пересекает ось x , x = −1 и x = 2 , являются решениями квадратного уравнения x ² − x − 2 = 0 .

В процессе заполнения квадрата используется алгебраическое тождество

${\displaystyle x^{2}+2hx+h^{2}=(x+h)^{2},}$

который представляет собой четко определенный алгоритм , который можно использовать для решения любого квадратного уравнения. ^{[6] : 207} Начнем с квадратного уравнения в стандартной форме: ax ² + bx + c = 0.

1. Разделите каждую сторону на коэффициент при квадрате члена.
2. Вычтите постоянный член c / a из обеих частей.
3. Прибавьте к обеим сторонам квадрат половины b / a , коэффициент x . Это «завершает квадрат», превращая левую сторону в идеальный квадрат.
4. Запишите левую часть в виде квадрата и при необходимости упростите правую сторону.
5. Составьте два линейных уравнения, приравняв квадратный корень из левой части к положительным и отрицательным квадратным корням из правой части.
6. Решите каждое из двух линейных уравнений.

Мы проиллюстрируем использование этого алгоритма, решив 2 x ² + 4 x − 4 = 0.

${\displaystyle 2x^{2}+4x-4=0}$

${\displaystyle \ x^{2}+2x-2=0}$

${\displaystyle \ x^{2}+2x=2}$

${\displaystyle \ x^{2}+2x+1=2+1}$

${\displaystyle \left(x+1\right)^{2}=3}$

${\displaystyle \ x+1=\pm {\sqrt {3}}}$

${\displaystyle \ x=-1\pm {\sqrt {3}}}$

Символ плюс-минус «±» указывает, что x = −1 + √ 3 и x = −1 − √ 3 являются решениями квадратного уравнения. ^[8]

Квадратичная формула и ее вывод

Заполнение квадрата можно использовать для вывода общей формулы решения квадратных уравнений, называемой квадратной формулой. ^[9] Математическое доказательство теперь будет кратко изложено. ^{[10] С помощью} полиномиального разложения легко увидеть, что следующее уравнение эквивалентно квадратному уравнению:

${\displaystyle \left(x+{\frac {b}{2a}}\right)^{2}={\frac {b^{2}-4ac}{4a^{2}}}.}$

Извлечение квадратного корня из обеих сторон и выделение x дает:

${\displaystyle x={\frac {-b\pm {\sqrt {b^{2}-4ac}}}{2a}}.}$

В некоторых источниках, особенно старых, используются альтернативные параметризации квадратного уравнения, такие как ax ² + 2 bx + c = 0 или ax ² - 2 bx + c = 0  , ^[11] где b имеет величину, составляющую половину более распространенной. один, возможно, с противоположным знаком. Это приводит к несколько разным формам решения, но в остальном эквивалентно.

В литературе можно найти ряд альтернативных выводов . Эти доказательства проще, чем стандартное завершение метода квадратов, представляют собой интересные применения других часто используемых методов алгебры или дают представление о других областях математики.

Менее известная квадратичная формула, используемая в методе Мюллера , дает те же корни через уравнение

${\displaystyle x={\frac {2c}{-b\pm {\sqrt {b^{2}-4ac}}}}.}$

Это можно вывести из стандартной квадратичной формулы по формулам Виеты , которые утверждают, что произведение корней равно c / a . Это также следует из разделения квадратного уравнения путем его решения и последующего обращения. ${\displaystyle x^{2}}$ ${\displaystyle cx^{-2}+bx^{-1}+a=0,}$ ${\displaystyle x^{-1},}$

Одним из свойств этой формы является то, что она дает один действительный корень, когда a = 0 , в то время как другой корень содержит деление на ноль, потому что, когда a = 0 , квадратное уравнение становится линейным уравнением, которое имеет один корень. Напротив, в этом случае более распространенная формула имеет деление на ноль для одного корня и неопределенную форму 0/0 для другого корня. С другой стороны, когда c = 0 , более распространенная формула дает два правильных корня, тогда как эта форма дает нулевой корень и неопределенную форму 0/0 .

Когда ни a , ни c не равны нулю, равенство между стандартной квадратичной формулой и методом Мюллера:

${\displaystyle {\frac {2c}{-b-{\sqrt {b^{2}-4ac}}}}={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\,,}$

можно проверить перекрестным умножением и аналогично для другого выбора знаков.

Приведенное квадратное уравнение

Иногда удобно привести квадратное уравнение так, чтобы его старший коэффициент был равен единице. Это делается путем деления обеих частей на a , что всегда возможно, поскольку a не равно нулю. В результате получается сокращенное квадратное уравнение : ^[12]

${\displaystyle x^{2}+px+q=0,}$

где p = b / a и q = c / a . Это моническое полиномиальное уравнение имеет те же решения, что и исходное.

Квадратная формула решения приведенного квадратного уравнения, записанная через его коэффициенты, имеет вид

${\displaystyle x={\frac {1}{2}}\left(-p\pm {\sqrt {p^{2}-4q}}\right)}$

или, что то же самое,

${\displaystyle x=-{\frac {p}{2}}\pm {\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}\,.}$

Дискриминант

Рисунок 3. Дискриминантные признаки

В квадратной формуле выражение под знаком квадратного корня называется дискриминантом квадратного уравнения и часто обозначается прописной буквой D или прописной греческой дельтой : ^[13]

${\displaystyle \Delta =b^{2}-4ac.}$

Квадратное уравнение с действительными коэффициентами может иметь один или два различных действительных корня или два различных комплексных корня. В этом случае дискриминант определяет количество и характер корней. Есть три случая:

• Если дискриминант положителен, то имеются два различных корня

${\displaystyle {\frac {-b+{\sqrt {\Delta }}}{2a}}\quad {\text{and}}\quad {\frac {-b-{\sqrt {\Delta }}}{2a}},}$

оба из которых являются действительными числами. Для квадратных уравнений с рациональными коэффициентами, если дискриминант представляет собой квадратное число , то корни рациональны; в других случаях они могут быть квадратичными иррациональными числами .

• Если дискриминант равен нулю, то существует ровно один действительный корень , который иногда называют повторяющимся или двойным корнем , или два равных корня. ${\displaystyle -{\frac {b}{2a}},}$

• Если дискриминант отрицательный, то действительных корней нет. Скорее, есть два различных (недействительных) комплексных корня ^[14] ${\displaystyle -{\frac {b}{2a}}+i{\frac {\sqrt {-\Delta }}{2a}}\quad {\text{and}}\quad -{\frac {b}{2a}}-i{\frac {\sqrt {-\Delta }}{2a}},}$

которые являются комплексно сопряженными друг с другом. В этих выражениях i — мнимая единица .

Таким образом, корни различны тогда и только тогда, когда дискриминант ненулевой, а корни действительны тогда и только тогда, когда дискриминант неотрицательен.

Геометрическая интерпретация

График y = ax ² + bx + c , где a и дискриминант b ² − 4 ac положительны, причем

• Корни и y -перехват выделены красным
• Вершина и ось симметрии выделены синим цветом.
• Фокус и директриса розового цвета.

Визуализация комплексных корней y = ax ² + bx + c : парабола повернута на 180° вокруг своей вершины ( оранжевый цвет ). Его точки пересечения с x повернуты на 90° вокруг своей средней точки, а декартова плоскость интерпретируется как комплексная плоскость ( зеленая ). ^[15]

Функция f ( x ) = ax ² + bx + c является квадратичной функцией . ^[16] График любой квадратичной функции имеет одну и ту же общую форму, которая называется параболой . Местоположение и размер параболы, а также то, как она открывается, зависят от значений a , b и c . Как показано на рисунке 1, если a > 0 , парабола имеет точку минимума и открывается вверх. Если a < 0 , парабола имеет максимальную точку и открывается вниз. Крайняя точка параболы, будь то минимальная или максимальная, соответствует ее вершине . Координата x вершины будет находиться в точке , а координату y вершины можно найти, подставив это значение x в функцию. Перехват y расположен в точке ( 0, c ) . ${\displaystyle \scriptstyle x={\tfrac {-b}{2a}}}$

Решения квадратного уравнения ax ² + bx + c = 0 соответствуют корням функции f ( x ) = ax ² + bx + c , поскольку они являются значениями x , для которых f ( x ) = 0 . Как показано на рисунке 2, если a , b и c — действительные числа , а область определения f — это набор действительных чисел, то корнями f являются в точности координаты x точек, в которых график касается оси x . . Как показано на рисунке 3, если дискриминант положителен, график касается оси x в двух точках; если ноль, график касается в одной точке; а если отрицательно, то график не касается оси x .

Квадратичная факторизация

Термин

${\displaystyle x-r}$

является фактором многочлена

${\displaystyle ax^{2}+bx+c}$

тогда и только тогда, когда r является корнем квадратного уравнения

${\displaystyle ax^{2}+bx+c=0.}$

Из квадратичной формулы следует, что

${\displaystyle ax^{2}+bx+c=a\left(x-{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}\right)\left(x-{\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}\right).}$

В частном случае b ² = 4 ac , когда квадратичный многочлен имеет только один отдельный корень ( т. е . дискриминант равен нулю), квадратичный многочлен можно разложить на множители как

${\displaystyle ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}.}$

Графическое решение

Рисунок 4. Вычисление графическим калькулятором одного из двух корней квадратного уравнения 2 x ² + 4 x − 4 = 0 . Хотя на дисплее отображается только пять значащих цифр точности, полученное значение xc составляет 0,732050807569, с точностью до двенадцати значащих цифр.

Квадратичная функция без вещественного корня: y = ( x − 5) ² + 9 . «3» — это мнимая часть точки пересечения с x . Действительная часть — это координата x вершины. Таким образом, корни равны 5 ± 3 i .

Решения квадратного уравнения

${\displaystyle ax^{2}+bx+c=0}$

можно вывести из графика квадратичной функции

${\displaystyle f(x)=ax^{2}+bx+c,}$

что является параболой .

Если парабола пересекает ось x в двух точках, то имеется два действительных корня , которые являются координатами x этих двух точек (также называемыми x -перехватом).

Если парабола касается оси x , то имеется двойной корень, который является координатой x точки контакта графика и параболы.

Если парабола не пересекает ось X , то имеются два комплексно-сопряженных корня. Хотя эти корни невозможно визуализировать на графике, их действительную и мнимую части можно. ^[17]

Пусть h и k - соответственно координата x и координата y вершины параболы (то есть точки с максимальной или минимальной координатой y . Квадратичную функцию можно переписать

${\displaystyle y=a(x-h)^{2}+k.}$

Пусть d — расстояние между точкой с координатой y 2 k на оси параболы и точкой на параболе с такой же координатой y (см. рисунок; таких точек две, дающих одинаковое расстояние, из-за симметрии параболы). Тогда действительная часть корней равна h , а их мнимая часть равна ± d . То есть корни

${\displaystyle h+id\quad {\text{and}}\quad h-id,}$

или в случае примера рисунка

${\displaystyle 5+3i\quad {\text{and}}\quad 5-3i.}$

Как избежать потери значимости

Хотя квадратичная формула обеспечивает точное решение, результат не является точным, если во время вычислений действительные числа аппроксимируются, как это обычно бывает в численном анализе , где действительные числа аппроксимируются числами с плавающей запятой (называемыми «действительными числами» во многих языках программирования ). В этом контексте квадратичная формула не является полностью устойчивой .

Это происходит, когда корни имеют разный порядок величины или, что то же самое, когда b ² и b ² − 4 ac близки по величине. В этом случае вычитание двух почти равных чисел приведет к потере значимости или катастрофическому сокращению меньшего корня. Чтобы избежать этого, корень меньшего размера, r , можно вычислить следующим образом: где R — корень большего размера. Это эквивалентно использованию формулы ${\displaystyle (c/a)/R}$

${\displaystyle x={\frac {-2c}{b\pm {\sqrt {b^{2}-4ac}}}}}$

используя знак плюс, если и знак минус, если ${\displaystyle b>0}$ ${\displaystyle b<0.}$

Вторая форма сокращения может произойти между членами b ² и 4 ac дискриминанта, то есть когда два корня очень близки. Это может привести к потере до половины правильных значащих цифр в корнях. ^{[11] [18]}

Примеры и приложения

Траектория прыгуна со скалы является параболической , поскольку горизонтальное смещение является линейной функцией времени , а вертикальное смещение является квадратичной функцией времени . В результате путь следует квадратному уравнению , где и — горизонтальная и вертикальная составляющие исходной скорости, a — ускорение свободного падения , а h — исходная высота. Здесь значение a следует считать отрицательным, так как его направление (вниз) противоположно измерению высоты (вверх). ${\displaystyle x=v_{x}t}$ ${\displaystyle y={\tfrac {1}{2}}at^{2}+v_{y}t+h}$ ${\displaystyle y={\tfrac {a}{2v_{x}^{2}}}x^{2}+{\tfrac {v_{y}}{v_{x}}}x+h}$ ${\displaystyle v_{x}}$ ${\displaystyle v_{y}}$

Золотое сечение находится как положительное решение квадратного уравнения. ${\displaystyle x^{2}-x-1=0.}$

Уравнения окружности и других конических сечений — эллипсов , парабол и гипербол — являются квадратными уравнениями с двумя переменными.

Учитывая косинус или синус угла, для нахождения косинуса или синуса угла, который вдвое меньше, необходимо решить квадратное уравнение.

Процесс упрощения выражений, включающих квадратный корень из выражения, включающего квадратный корень из другого выражения, включает в себя нахождение двух решений квадратного уравнения.

Теорема Декарта утверждает, что радиусы каждых четырех целующихся (взаимно касающихся) кругов удовлетворяют определенному квадратному уравнению.

Уравнение, заданное теоремой Фусса , определяющее связь между радиусом вписанной в бицентрический четырёхугольник окружностью , радиусом описанной в нём окружности и расстоянием между центрами этих окружностей, может быть выражено в виде квадратного уравнения, для которого расстояние между центрами двух кругов через их радиусы является одним из решений. Другое решение того же уравнения в терминах соответствующих радиусов дает расстояние между центром описанной окружности и центром вписанной окружности экс - касательного четырехугольника .

Критические точки кубической функции и точки перегиба функции четвертой степени находятся путем решения квадратного уравнения.

История

Вавилонские математики еще в 2000 году до нашей эры (отображены на старовавилонских глиняных табличках ) могли решать задачи, связанные с площадями и сторонами прямоугольников. Есть свидетельства, датирующие этот алгоритм еще Третьей династией Ура . ^[19] В современных обозначениях проблемы обычно включают решение пары одновременных уравнений вида:

${\displaystyle x+y=p,\ \ xy=q,}$

что эквивалентно утверждению, что x и y являются корнями уравнения: ^{[20] : 86}

${\displaystyle z^{2}+q=pz.}$

Шаги, данные вавилонскими писцами для решения вышеупомянутой проблемы прямоугольника в терминах x и y , были следующими:

1. Вычислите половину p .
2. Возведите результат в квадрат.
3. Вычтите q .
4. Найдите (положительный) квадратный корень, используя таблицу квадратов.
5. Сложите результаты шагов (1) и (4), чтобы получить x .

В современных обозначениях это означает вычисление , что эквивалентно современной квадратичной формуле для большего действительного корня (если таковой имеется) с a = 1 , b = - p и c = q . ${\displaystyle x=\left({\frac {p}{2}}\right)+{\sqrt {\left({\frac {p}{2}}\right)^{2}-q}}}$ ${\displaystyle x={\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}}}$

Геометрические методы использовались для решения квадратных уравнений в Вавилонии, Египте, Греции, Китае и Индии. Египетский берлинский папирус , относящийся к Среднему царству (2050–1650 гг. до н.э.), содержит решение двухчленного квадратного уравнения. ^[21] Вавилонские математики примерно 400 г. до н.э. и китайские математики примерно 200 г. до н.э. использовали геометрические методы рассечения для решения квадратных уравнений с положительными корнями. ^{[22] [23]} Правила для квадратных уравнений были даны в « Девяти главах математического искусства» , китайском трактате по математике. ^{[23] [24]} Эти ранние геометрические методы, похоже, не имели общей формулы. Евклид , греческий математик , разработал более абстрактный геометрический метод около 300 г. до н.э. Используя чисто геометрический подход, Пифагор и Евклид создали общую процедуру поиска решений квадратного уравнения. В своей работе «Арифметика» греческий математик Диофант решил квадратное уравнение, но дал только один корень, даже если оба корня были положительными. ^[25]

В 628 году нашей эры Брахмагупта , индийский математик , дал в своей книге «Брахмаспхутасиддханта» первое явное (хотя и не совсем общее) решение квадратного уравнения ax ² + bx = c следующим образом: «Для абсолютного числа, умноженного на четыре раза, [ коэффициент] квадрата, сложите квадрат [коэффициента] среднего члена; квадратный корень из того же самого, за вычетом [коэффициента] среднего члена, разделите на два [коэффициент] квадрата и есть значение ." ^[26] Это эквивалентно

${\displaystyle x={\frac {{\sqrt {4ac+b^{2}}}-b}{2a}}.}$

Рукопись Бахшали , написанная в Индии в VII веке нашей эры, содержала алгебраическую формулу для решения квадратных уравнений, а также квадратных неопределенных уравнений (первоначально типа ax / c = y ^{[ необходимо уточнение : оно линейное, а не квадратное ]} ). Мухаммад ибн Муса аль-Хорезми (9 век), возможно, вдохновленный Брахмагуптой, ^{[ оригинальное исследование? ]} разработал набор формул, которые помогали найти положительные решения. Аль-Хорезми идет дальше, предоставляя полное решение общего квадратного уравнения, принимая один или два числовых ответа для каждого квадратного уравнения, одновременно предоставляя геометрические доказательства в процессе. ^[27] Он также описал метод завершения квадрата и признал, что дискриминант должен быть положительным, ^{[27] [28] : 230} , что было доказано его современником Абд аль-Хамидом ибн Тюрком (Средняя Азия, 9 век), который дал геометрические фигуры, чтобы доказать, что если дискриминант отрицательный, то квадратное уравнение не имеет решения. ^{[28] : 234} Хотя сам аль-Хорезми не принимал отрицательных решений, более поздние исламские математики , пришедшие ему на смену, принимали в качестве решений отрицательные решения, ^{[27] : 191} , а также иррациональные числа . ^[29] Абу Камиль Шуджа ибн Аслам (Египет, 10 век), в частности, был первым, кто принял иррациональные числа (часто в форме квадратного корня , кубического корня или корня четвертой степени ) в качестве решений квадратных уравнений или в качестве коэффициентов в уравнении. . ^[30] Индийский математик 9-го века Шридхара записал правила решения квадратных уравнений. ^[31]

Еврейский математик Авраам бар Хийя Ха-Наси (12 век, Испания) является автором первой европейской книги, включающей полное решение общего квадратного уравнения. ^[32] Его решение во многом основывалось на работе Аль-Хорезми. ^[27] Сочинение китайского математика Ян Хуэя (1238–1298 гг. н. э.) является первым известным произведением, в котором появляются квадратные уравнения с отрицательными коэффициентами при «x», хотя он приписывает это более раннему Лю И. ^[33] К 1545 году Джероламо Кардано собрал труды, связанные с квадратными уравнениями. Квадратичная формула, охватывающая все случаи, была впервые получена Симоном Стевеном в 1594 году. ^[34] В 1637 году Рене Декарт опубликовал «Геометрию» , содержащую квадратичную формулу в той форме, которую мы знаем сегодня.

Расширенные темы

Альтернативные методы вычисления корня

Формулы Виеты

График разницы аппроксимации Виета для наименьшего корня квадратного уравнения x ² + bx + c = 0 по сравнению со значением, рассчитанным по квадратной формуле

Формулы Виеты (названные в честь Франсуа Вьета ) представляют собой отношения

${\displaystyle x_{1}+x_{2}=-{\frac {b}{a}},\quad x_{1}x_{2}={\frac {c}{a}}}$

между корнями квадратного многочлена и его коэффициентами. Они являются результатом почленного сравнения отношения

${\displaystyle \left(x-x_{1}\right)\left(x-x_{2}\right)=x^{2}-\left(x_{1}+x_{2}\right)x+x_{1}x_{2}=0}$

с уравнением

${\displaystyle x^{2}+{\frac {b}{a}}x+{\frac {c}{a}}=0.}$

Первая формула Виеты полезна для построения графика квадратичной функции. Поскольку граф симметричен относительно вертикальной линии, проходящей через вершину , координата x вершины находится в среднем значении корней (или точек пересечения). Таким образом, координата x вершины равна

${\displaystyle x_{V}={\frac {x_{1}+x_{2}}{2}}=-{\frac {b}{2a}}.}$

Координата y может быть получена путем подстановки приведенного выше результата в данное квадратное уравнение, что дает

${\displaystyle y_{V}=-{\frac {b^{2}}{4a}}+c=-{\frac {b^{2}-4ac}{4a}}.}$

Также эти формулы для вершины можно вывести непосредственно из формулы (см. Заполнение квадрата )

${\displaystyle ax^{2}+bx+c=a\left(x+{\frac {b}{2a}}\right)^{2}-{\frac {b^{2}-4ac}{4a}}.}$

Для численных вычислений формулы Виеты предоставляют полезный метод поиска корней квадратного уравнения в случае, когда один корень намного меньше другого. Если | х ₂ | << | х ₁ | , то x ₁ + x ₂ ≈ x ₁ и имеем оценку:

${\displaystyle x_{1}\approx -{\frac {b}{a}}.}$

Тогда вторая формула Виеты дает:

${\displaystyle x_{2}={\frac {c}{ax_{1}}}\approx -{\frac {c}{b}}.}$

Эти формулы гораздо легче вычислить, чем квадратную формулу при условии наличия одного большого и одного маленького корня, поскольку квадратичная формула оценивает малый корень как разность двух почти равных чисел (случай большого b ), что приводит к округлению -off ошибка в числовой оценке. На рисунке показана разница между ^{[ необходимы пояснения ]} (i) прямой оценкой с использованием квадратичной формулы (точно, когда корни близки по значению) и (ii) оценкой, основанной на приведенной выше аппроксимации формул Виеты (точно, когда корни широко расставлены). По мере увеличения линейного коэффициента b изначально квадратичная формула является точной, а точность приближенной формулы улучшается, что приводит к уменьшению разницы между методами по мере увеличения b . Однако в какой-то момент квадратичная формула начинает терять точность из-за ошибки округления, а приближенный метод продолжает совершенствоваться. Следовательно, разница между методами начинает увеличиваться по мере ухудшения квадратичной формулы.

Такая ситуация обычно возникает при проектировании усилителей, где для обеспечения стабильной работы требуется широко разнесенные корни (см. Переходный процесс ).

Тригонометрическое решение

Во времена, когда еще не существовало калькуляторов, люди использовали математические таблицы — списки чисел, показывающие результаты вычислений с различными аргументами, — чтобы упростить и ускорить вычисления. Таблицы логарифмов и тригонометрических функций были распространены в учебниках математики и естественных наук. Были опубликованы специализированные таблицы для таких приложений, как астрономия, небесная навигация и статистика. Существовали методы числовой аппроксимации, называемые простафаэрезом , которые позволяли сократить время выполнения трудоемких операций, таких как умножение, извлечение степеней и корней. ^[35] Астрономов особенно интересовали методы, которые могли бы ускорить длинные серии вычислений, связанных с расчетами небесной механики .

Именно в этом контексте мы можем понять развитие средств решения квадратных уравнений с помощью тригонометрической замены . Рассмотрим следующую альтернативную форму квадратного уравнения:

[1]   ${\displaystyle ax^{2}+bx\pm c=0,}$

где знак символа ± выбран так, чтобы оба a и c могли быть положительными. Подставив

[2]   ${\displaystyle x={\sqrt {c/a}}\tan \theta }$

а затем умножив на cos ² ( θ ) / c , мы получим

[3]   ${\displaystyle \sin ^{2}\theta +{\frac {b}{\sqrt {ac}}}\sin \theta \cos \theta \pm \cos ^{2}\theta =0.}$

Вводя функции от 2 θ и переставляя, получаем

[4]   ${\displaystyle \tan 2\theta _{n}=+2{\frac {\sqrt {ac}}{b}},}$

[5]   ${\displaystyle \sin 2\theta _{p}=-2{\frac {\sqrt {ac}}{b}},}$

где индексы n и p соответствуют использованию отрицательного или положительного знака в уравнении [1] соответственно . Подстановка двух значений θ _n или θ _p , найденных из уравнений [4] или [5] в [2] , дает требуемые корни из [1] . Комплексные корни возникают в решении на основе уравнения [5] , если абсолютное значение sin 2 θ _p превышает единицу. Объем усилий, затраченных на решение квадратных уравнений с использованием этой смешанной стратегии поиска в тригонометрической и логарифмической таблице, составил две трети усилий, затраченных на использование только логарифмических таблиц. ^[36] Вычисление комплексных корней потребует использования другой тригонометрической формы. ^[37]

Для иллюстрации предположим, что у нас есть семизначный логарифм и тригонометрические таблицы, и мы хотим решить следующую задачу с точностью до шести значащих цифр:

${\displaystyle 4.16130x^{2}+9.15933x-11.4207=0}$

1. Таблица поиска из семи позиций может содержать только 100 000 записей, а вычисление промежуточных результатов по семи позициям обычно требует интерполяции между соседними записями.
2. ${\displaystyle \log a=0.6192290,\log b=0.9618637,\log c=1.0576927}$
3. ${\displaystyle 2{\sqrt {ac}}/b=2\times 10^{(0.6192290+1.0576927)/2-0.9618637}=1.505314}$
4. ${\displaystyle \theta =(\tan ^{-1}1.505314)/2=28.20169^{\circ }{\text{ or }}-61.79831^{\circ }}$
5. ${\displaystyle \log |\tan \theta |=-0.2706462{\text{ or }}0.2706462}$
6. ${\displaystyle \log {\sqrt {c/a}}=(1.0576927-0.6192290)/2=0.2192318}$
7. ${\displaystyle x_{1}=10^{0.2192318-0.2706462}=0.888353}$(округлено до шести значащих цифр)

${\displaystyle x_{2}=-10^{0.2192318+0.2706462}=-3.08943}$

Решение комплексных корней в полярных координатах

Если квадратное уравнение с действительными коэффициентами имеет два комплексных корня - случай, когда требуется, чтобы a и c имели одинаковый знак друг друга - тогда решения для корней могут быть выражены в полярной форме как ^[38] ${\displaystyle ax^{2}+bx+c=0}$ ${\displaystyle b^{2}-4ac<0,}$

${\displaystyle x_{1},\,x_{2}=r(\cos \theta \pm i\sin \theta ),}$

где и ${\displaystyle r={\sqrt {\tfrac {c}{a}}}}$ ${\displaystyle \theta =\cos ^{-1}\left({\tfrac {-b}{2{\sqrt {ac}}}}\right).}$

Геометрическое решение

Рисунок 6. Геометрическое решение ax ² + bx + c = 0 с использованием метода Лилля. Решения: −AX1/SA, −AX2/SA.

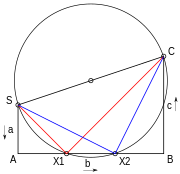
Квадратное уравнение можно решить геометрически несколькими способами. Один из способов — метод Лилля . Три коэффициента a , b , c нарисованы с прямыми углами между ними, как в SA, AB и BC на рисунке 6. Нарисован круг с начальной и конечной точкой SC в качестве диаметра. Если это пересекает среднюю линию AB из трех, то уравнение имеет решение, и решения даются отрицательным расстоянием вдоль этой линии от A, деленным на первый коэффициент a или SA. Если a равно 1, коэффициенты можно считывать напрямую. Таким образом, решения на диаграмме — −AX1/SA и −AX2/SA. ^[39]

Окружность Карлейля квадратного уравнения x ²  −  sx  +  p  = 0.

Круг Карлейля , названный в честь Томаса Карлейля , обладает тем свойством, что решениями квадратного уравнения являются горизонтальные координаты пересечений круга с горизонтальной осью . ^[40] Круги Карлейля использовались для разработки конструкций правильных многоугольников в виде линейки и циркуля .

Обобщение квадратного уравнения

Формула и ее вывод остаются верными, если коэффициенты a , b и c являются комплексными числами или, в более общем смысле, членами любого поля , характеристика которого не равна 2 . (В поле характеристики 2 элемент 2a равен нулю и делить на него нельзя.)

Символ

${\displaystyle \pm {\sqrt {b^{2}-4ac}}}$

в формуле следует понимать «любой из двух элементов, квадрат которых равен b ² − 4 ac , если такие элементы существуют». В некоторых полях некоторые элементы не имеют квадратных корней, а некоторые имеют два; только ноль имеет только один квадратный корень, за исключением полей характеристики 2 . Даже если поле не содержит квадратного корня из некоторого числа, всегда существует поле квадратичного расширения, которое его содержит, поэтому квадратичная формула всегда будет иметь смысл как формула в этом поле расширения.

Характеристика 2

В поле характеристики 2 квадратичная формула, основанная на том, что 2 является единицей , не выполняется. Рассмотрим приведенный квадратичный полином

${\displaystyle x^{2}+bx+c}$

над полем характеристики 2 . Если b = 0 , то решение сводится к извлечению квадратного корня, поэтому решение имеет вид

${\displaystyle x={\sqrt {c}}}$

и имеет только один корень, так как

${\displaystyle -{\sqrt {c}}=-{\sqrt {c}}+2{\sqrt {c}}={\sqrt {c}}.}$

В итоге,

${\displaystyle \displaystyle x^{2}+c=(x+{\sqrt {c}})^{2}.}$

См. квадратичный вычет для получения дополнительной информации об извлечении квадратных корней в конечных полях.

В случае, когда b ≠ 0 , есть два различных корня, но если многочлен неприводим , они не могут быть выражены через квадратные корни из чисел в поле коэффициентов. Вместо этого определите 2-корень R ( c ) из c как корень многочлена x ² + x + c , элемента поля расщепления этого многочлена. Проверяется, что R ( c ) + 1 также является корнем. С точки зрения операции с двумя корнями два корня (немонического) квадратичного ax ² + bx + c равны

${\displaystyle {\frac {b}{a}}R\left({\frac {ac}{b^{2}}}\right)}$

и

${\displaystyle {\frac {b}{a}}\left(R\left({\frac {ac}{b^{2}}}\right)+1\right).}$

Например, пусть a обозначает мультипликативный генератор группы единиц F ₄ , поля Галуа четвертого порядка (таким образом, a и a + 1 являются корнями x ² + x + 1 над F ₄ . Поскольку ( a + 1) ² = a , a + 1 — единственное решение квадратного уравнения x ² + a = 0. С другой стороны, многочлен x ² + ax + 1 неприводим над F ₄ , но расщепляется над F ₁₆ , где _имеет два корня ab и ab + a , где b — корень x2 + x + ^a в F16 .

Это частный случай теории Артина-Шрайера .

Смотрите также

• Решение квадратных уравнений с цепными дробями
• Линейное уравнение
• Кубическая функция
• Уравнение четвертой степени
• Уравнение квинтики
• Основная теорема алгебры

Рекомендации

1. Чарльз П. МакКег (2014). Промежуточная алгебра с тригонометрией (переиздание). Академическая пресса. п. 219. ИСБН 978-1-4832-1875-5.Выдержка со страницы 219
2. Проттерс и Морри: «Исчисление и аналитическая геометрия. Первый курс».
3. Принстонский обзор (2020). Princeton Review SAT Prep, 2021: 5 практических тестов + обзор и методы + онлайн-инструменты. Детские книги случайного дома. п. 360. ИСБН 978-0-525-56974-9.Выдержка со страницы 360
4. Дэвид Мамфорд; Кэролайн Серия; Дэвид Райт (2002). Жемчуг Индры: Видение Феликса Кляйна (иллюстрировано, переиздано под ред.). Издательство Кембриджского университета. п. 37. ИСБН 978-0-521-35253-6.Выдержка со страницы 37
5. Справочник для учителей «Математика в действии», 4b (иллюстрированное издание). Нельсон Торнс. 1996. с. 26. ISBN 978-0-17-431439-4.Выдержка со страницы 26
6. Вашингтон, Аллин Дж. (2000). Основная техническая математика с исчислением, седьмое издание . ISBN Аддисона Уэсли Лонгмана, Inc. 978-0-201-35666-3.
7. Эббингауз, Хайнц-Дитер; Юинг, Джон Х. (1991), Числа, тексты для выпускников по математике, том. 123, Спрингер, с. 77, ISBN 9780387974972.
8. Стерлинг, Мэри Джейн (2010), Алгебра I для чайников, Wiley Publishing, стр. 219, ISBN 978-0-470-55964-2
9. Рич, Барнетт; Шмидт, Филип (2004), Очерк теории и проблем элементарной алгебры Шаума , The McGraw-Hill Companies, ISBN 978-0-07-141083-0, глава 13 §4.4, с. 291
10. Химонас, Алекс. Исчисление для бизнеса и социальных наук , с. 64 (Публикации Ричарда Денниса, 2001).
11. Кахан, Виллиан (20 ноября 2004 г.), О стоимости вычислений с плавающей запятой без сверхточной арифметики (PDF) , получено 25 декабря 2012 г.
12. Аленицын, Александр и Бутиков, Евгений. Краткий справочник по математике и физике , с. 38 (CRC Press, 1997)
13. Δ — начальная буква греческого слова Δ ιακρίνουσα, Diakrínoousa , дискриминант.
14. Ахац, Томас; Андерсон, Джон Г.; Маккензи, Кэтлин (2005). Технический цех Математика. Промышленная пресса. п. 277. ИСБН 978-0-8311-3086-2.
15. «Сложные корни стали видимыми - забавные факты о математике» . Проверено 1 октября 2016 г.
16. Уортон, П. (2006). Основы Edexcel Gcse Math/Higher. Лонсдейл. п. 63. ИСБН 978-1-905-129-78-2.
17. Алек Нортон, Бенджамин Лотто (июнь 1984 г.), «Комплексные корни стали видимыми», The College Mathematics Journal , 15 (3): 248–249, doi : 10.2307/2686333, JSTOR  2686333
18. Хайэм, Николас (2002), Точность и стабильность числовых алгоритмов (2-е изд.), SIAM, стр. 10, ISBN 978-0-89871-521-7
19. Фриберг, Йоран (2009). «Геометрический алгоритм с решениями квадратных уравнений в шумерском юридическом документе из Ура III Уммы». Журнал клинописной цифровой библиотеки . 3 .
20. Стиллвелл, Джон (2004). Математика и ее история (2-е изд.) . Спрингер. ISBN 978-0-387-95336-6.
21. Кембриджская древняя история, часть 2. Ранняя история Ближнего Востока. Издательство Кембриджского университета. 1971. с. 530. ИСБН 978-0-521-07791-0.
22. Хендерсон, Дэвид В. «Геометрические решения квадратных и кубических уравнений». Математический факультет Корнелльского университета . Проверено 28 апреля 2013 г.
23. Эйткен, Уэйн. «Китайская классика: девять глав» (PDF) . Математический факультет Калифорнийского государственного университета . Проверено 28 апреля 2013 г.
24. Смит, Дэвид Юджин (1958). История математики. Публикации Courier Dover. п. 380. ИСБН 978-0-486-20430-7.
25. Смит, Дэвид Юджин (1958). История математики, Том 1 . Courier Dover Publications. п. 134. ИСБН 978-0-486-20429-1.Выдержка со страницы 134
26. Брахмасфутасиддханта, перевод Коулбрука, 1817 г., стр. 346; цитируется Стиллвеллом, Джоном (2010). Математика и ее история (3-е изд.) . Спрингер. п. 93. дои : 10.1007/978-1-4419-6053-5. ISBN 978-0-387-95336-6.
27. Кац, виджей; Бартон, Б. (2006). «Этапы истории алгебры, имеющие значение для преподавания». Образовательные исследования по математике . 66 (2): 185–201. дои : 10.1007/s10649-006-9023-7. S2CID  120363574.
28. Бойер, Карл Б.; Ута К. Мерцбах , преп. редактор (1991). История математики. Джон Уайли и сыновья, Inc. ISBN 978-0-471-54397-8. {{cite book}}: |first=имеет общее имя ( справка )CS1 maint: multiple names: authors list (link)
29. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. (1999), «Арабская математика: забытое великолепие?», Архив истории математики MacTutor , Университет Сент-Эндрюс«Алгебра была объединяющей теорией, которая позволяла рассматривать рациональные числа, иррациональные числа, геометрические величины и т. д. как «алгебраические объекты».»
30. Жак Сезиано, «Исламская математика», с. 148, в Селине, Хелейн ; Д'Амброзио, Убиратан , ред. (2000), Математика в разных культурах: история незападной математики , Springer , ISBN 978-1-4020-0260-1
31. Смит, Дэвид Юджин (1958). История математики. Публикации Courier Dover. п. 280. ИСБН 978-0-486-20429-1.
32. Ливио, Марио (2006). Уравнение, которое невозможно решить. Саймон и Шустер. ISBN 978-0743258210.
33. Ронан, Колин (1985). Краткая наука и цивилизация в Китае. Издательство Кембриджского университета. п. 15. ISBN 978-0-521-31536-4.
34. Струйк, диджей; Стевин, Саймон (1958), Основные работы Саймона Стевина, Математика (PDF) , том. II–B, CV Swets & Zeitlinger, с. 470
35. Баллью, Пэт. «Решение квадратных уравнений — аналитическими и графическими методами; включая несколько методов, которые вы, возможно, никогда не видели» (PDF) . Архивировано из оригинала (PDF) 9 апреля 2011 года . Проверено 18 апреля 2013 г.
36. Сирс, FH (1945). «Тригонометрическое решение квадратного уравнения». Публикации Тихоокеанского астрономического общества . 57 (339): 307–309. Бибкод : 1945PASP...57..307S. дои : 10.1086/125759 .
37. Од, HTR (1938). «Решения квадратного уравнения, полученные с помощью тригонометрии». Национальный математический журнал . 13 (3): 118–121. дои : 10.2307/3028750. JSTOR  3028750.
38. Саймонс, Стюарт, «Альтернативный подход к комплексным корням действительных квадратных уравнений», Mathematical Gazette 93, март 2009 г., 91–92.
39. Биксби, Уильям Герберт (1879), Графический метод для быстрого поиска действительных корней числовых уравнений любой степени , Вест-Пойнт, штат Нью-Йорк
40. Вайсштейн, Эрик В. «Карлайл Серкл». Из MathWorld — веб-ресурса Wolfram . Проверено 21 мая 2013 г.

Внешние ссылки

• «Квадратное уравнение», Математическая энциклопедия , EMS Press , 2001 [1994]
• Вайсштейн, Эрик В. «Квадратные уравнения». Математический мир .
• 101 использование квадратного уравнения. Архивировано 10 ноября 2007 г. в Wayback Machine.
• 101 использование квадратного уравнения: Часть II. Архивировано 22 октября 2007 г. в Wayback Machine.