stringtranslate.com

Процесс аналитической иерархии

Простая иерархия AHP с окончательными приоритетами. Цель состоит в том, чтобы выбрать наиболее подходящего лидера из трех кандидатов. Факторы, которые следует учитывать, — это опыт, образование, харизма и возраст. Согласно суждениям лиц, принимающих решения, Дик — самый сильный кандидат, за ним следует Том, затем Гарри. Их процесс принятия решения подробно описан в приложении к этой статье .

В теории принятия решений аналитический иерархический процесс ( AHP ), также аналитический иерархический процесс , [1] представляет собой структурированную методику организации и анализа сложных решений , основанную на математике и психологии . Он был разработан Томасом Л. Саати в 1970-х годах; Саати сотрудничал с Эрнестом Форманом для разработки программного обеспечения Expert Choice в 1983 году, и с тех пор AHP был тщательно изучен и усовершенствован. Он представляет собой точный подход к количественной оценке весов критериев принятия решений. Опыт отдельных экспертов используется для оценки относительных величин факторов посредством попарных сравнений. Каждый из респондентов сравнивает относительную важность каждой пары элементов, используя специально разработанную анкету. Относительную важность критериев можно определить с помощью AHP путем сравнения критериев и, если применимо, подкритериев в парах экспертами или лицами, принимающими решения. На этой основе может быть найдена лучшая альтернатива. [2]

Использование и применение

AHP ориентирован на групповое принятие решений [ 3] и используется в ситуациях принятия решений в таких областях, как государственное управление, бизнес, промышленность [4] , здравоохранение и образование.

Вместо того, чтобы предписывать «правильное» решение, AHP помогает лицам, принимающим решения, найти решение, которое наилучшим образом соответствует их цели и пониманию проблемы. Он предоставляет всеобъемлющую и рациональную основу для структурирования проблемы принятия решения, для представления и количественной оценки ее элементов, для соотнесения этих элементов с общими целями и для оценки альтернативных решений.

Пользователи AHP сначала разлагают свою проблему принятия решения на иерархию более легко понимаемых подзадач, каждую из которых можно анализировать независимо. Элементы иерархии могут относиться к любому аспекту проблемы принятия решения — осязаемому или неосязаемому, тщательно измеренному или грубо оцененному, хорошо или плохо понятому — всему, что применимо к текущему решению.

После того, как иерархия построена, лица, принимающие решения, оценивают ее различные элементы, сравнивая их друг с другом по два за раз, с учетом их влияния на элемент, который находится выше в иерархии. При проведении сравнений лица, принимающие решения, могут использовать конкретные данные об элементах, а также свои суждения об относительном значении и важности элементов. При выполнении оценок могут использоваться человеческие суждения, а не только базовая информация. [5]

AHP преобразует эти оценки в числовые значения, которые можно обрабатывать и сравнивать по всему диапазону проблемы. Для каждого элемента иерархии выводится числовой вес или приоритет, что позволяет сравнивать различные и часто несоизмеримые элементы друг с другом рациональным и последовательным образом. Эта возможность отличает AHP от других методов принятия решений.

На последнем этапе процесса для каждой из альтернатив решения вычисляются числовые приоритеты. Эти числа представляют относительную способность альтернатив достигать цели решения, поэтому они позволяют прямо рассматривать различные варианты действий.

Хотя его могут использовать отдельные лица, работающие над простыми решениями, процесс аналитической иерархии (AHP) наиболее полезен там, где группы людей работают над сложными проблемами, особенно с высокими ставками, включающими человеческое восприятие и суждения, решения которых имеют долгосрочные последствия. [6]

Ситуации принятия решений, к которым может быть применен AHP, включают: [1]

Приложения AHP включают планирование , распределение ресурсов , установление приоритетов и выбор среди альтернатив. [6] Другие области включают прогнозирование , общее управление качеством , реинжиниринг бизнес-процессов , развертывание функций качества и сбалансированную систему показателей . [1] Другие применения AHP обсуждаются в литературе:

AHP иногда используется при разработке весьма специфических процедур для конкретных ситуаций, таких как рейтинг зданий по исторической значимости. [15] Недавно он был применен к проекту, который использует видеоматериалы для оценки состояния автомагистралей в Вирджинии . Инженеры-дорожники сначала использовали его для определения оптимального объема проекта , а затем для обоснования его бюджета перед законодателями . [16]

Веса матрицы суждений AHP могут быть скорректированы с помощью тех, которые рассчитаны с помощью метода энтропии. Этот вариант метода AHP называется AHP-EM. [13] [17]

Образование и научные исследования

Хотя использование аналитического иерархического процесса не требует специальной академической подготовки, он считается важным предметом во многих высших учебных заведениях, включая школы инженерии [18] и аспирантуры бизнеса . [19] Это особенно важный предмет в области качества , и его преподают на многих специализированных курсах, включая Six Sigma , Lean Six Sigma и QFD . [20] [21] [22]

Международный симпозиум по аналитической иерархии (ISAHP) проводит двухгодичные встречи ученых и практиков, интересующихся этой областью. Охватывается широкий спектр тем. В 2005 году они варьировались от «Установления стандартов оплаты для хирургических специалистов» до «Стратегического технологического дорожного картирования» и «Восстановления инфраструктуры в опустошенных странах». [23] На встрече 2007 года в Вальпараисо, Чили , было представлено 90 докладов из 19 стран, включая США, Германию, Японию, Чили, Малайзию и Непал. [24] Аналогичное количество докладов было представлено на симпозиуме 2009 года в Питтсбурге, Пенсильвания , где было представлено 28 стран. [25] Темы докладов включали экономическую стабилизацию в Латвии , выбор портфеля в банковском секторе , управление лесными пожарами для смягчения последствий глобального потепления и сельские микропроекты в Непале .

Использовать

Типичное устройство для ввода суждений в сеансе принятия решений группы AHP

Как можно увидеть в следующем материале, использование AHP подразумевает математический синтез многочисленных суждений о рассматриваемой проблеме принятия решения. Нередко эти суждения исчисляются десятками или даже сотнями. Хотя математические расчеты можно выполнять вручную или с помощью калькулятора, гораздо чаще используется один из нескольких компьютерных методов ввода и синтеза суждений. Простейшие из них включают стандартное программное обеспечение для электронных таблиц, в то время как самые сложные используют пользовательское программное обеспечение, часто дополненное специальными устройствами для получения суждений лиц, принимающих решения, собравшихся в зале заседаний.

Процедуру использования AHP можно обобщить следующим образом:

  1. Смоделируйте проблему в виде иерархии, содержащей цель решения, альтернативы ее достижения и критерии оценки альтернатив.
  2. Установите приоритеты среди элементов иерархии, сделав ряд суждений на основе парных сравнений элементов. Например, сравнивая потенциальные покупки коммерческой недвижимости, инвесторы могут сказать, что они предпочитают местоположение цене, а цену времени.
  3. Синтезируйте эти суждения, чтобы получить набор общих приоритетов для иерархии. Это объединит суждения инвесторов о местоположении, цене и сроках для объектов недвижимости A, B, C и D в общие приоритеты для каждого объекта недвижимости.
  4. Проверьте последовательность суждений.
  5. Примите окончательное решение на основе результатов этого процесса. [26]

Более подробно эти шаги описаны ниже.

Смоделируйте проблему как иерархию

Первым шагом в процессе аналитической иерархии является моделирование проблемы как иерархии. При этом участники изучают аспекты проблемы на уровнях от общего до детального, а затем выражают ее многоуровневым образом, как того требует AHP. Работая над построением иерархии, они повышают свое понимание проблемы, ее контекста, а также мыслей и чувств друг друга по поводу того и другого. [26]

Определены иерархии

Иерархия — это стратифицированная система ранжирования и организации людей, вещей, идей и т. д., где каждый элемент системы, за исключением самого верхнего, подчиняется одному или нескольким другим элементам. Хотя концепция иерархии легко понятна интуитивно, ее также можно описать математически. [27] Диаграммы иерархий часто имеют форму, близкую к пирамидам, но, за исключением наличия одного элемента наверху, в иерархии нет ничего обязательно пирамидального.

Человеческие организации часто структурированы как иерархии, где иерархическая система используется для распределения обязанностей, осуществления лидерства и облегчения коммуникации. Знакомые иерархии «вещей» включают в себя башенный блок настольного компьютера на «верху», с подчиненными ему монитором, клавиатурой и мышью «ниже».

В мире идей мы используем иерархии, чтобы помочь нам получить детальное знание сложной реальности: мы структурируем реальность в ее составные части, а те в свою очередь в свои собственные составные части, продвигаясь вниз по иерархии на столько уровней, сколько нам нужно. На каждом шагу мы фокусируемся на понимании одного компонента целого, временно игнорируя другие компоненты на этом и всех других уровнях. Проходя через этот процесс, мы увеличиваем наше глобальное понимание любой сложной реальности, которую мы изучаем.

Подумайте об иерархии, которую студенты-медики используют при изучении анатомии — они отдельно рассматривают опорно-двигательную систему (включая части и подчасти, такие как рука и ее составляющие мышцы и кости), кровеносную систему (и ее многочисленные уровни и ветви), нервную систему (и ее многочисленные компоненты и подсистемы) и т. д., пока не охватят все системы и важные подразделения каждой из них. Продвинутые студенты продолжают подразделение вплоть до уровня клетки или молекулы. В конце концов студенты понимают «общую картину» и значительное количество ее деталей. Более того, они понимают связь отдельных частей с целым. Работая иерархически, они обрели всестороннее понимание анатомии.

Аналогично, когда мы подходим к сложной проблеме принятия решения, мы можем использовать иерархию для интеграции больших объемов информации в наше понимание ситуации. По мере того, как мы выстраиваем эту информационную структуру, мы формируем все более и более качественную картину проблемы в целом. [26]

Иерархии в AHP

Иерархия AHP — это структурированное средство моделирования решения, которое находится в данный момент. Она состоит из общей цели, группы вариантов или альтернатив для достижения цели и группы факторов или критериев, которые связывают альтернативы с целью. Критерии могут быть далее разбиты на подкритерии, под-подкритерии и так далее, на столько уровней, сколько требует проблема. Критерий может применяться не единообразно, но может иметь градуированные различия, например, немного сладости приятно, но слишком много сладости может быть вредно. В этом случае критерий делится на подкритерии, указывающие на различные интенсивности критерия, например: мало, средне, высоко, и эти интенсивности ранжируются по приоритетам посредством сравнений в рамках родительского критерия сладости. Опубликованные описания приложений AHP часто включают диаграммы и описания их иерархий; некоторые простые показаны в этой статье. Более сложные иерархии AHP были собраны и переизданы как минимум в одной книге. [28] Более сложные иерархии можно найти на специальной странице обсуждения этой статьи .

Дизайн любой иерархии AHP будет зависеть не только от характера рассматриваемой проблемы, но и от знаний, суждений, ценностей, мнений, потребностей, желаний и т. д. участников процесса принятия решений. Построение иерархии обычно включает в себя значительное обсуждение, исследование и открытие теми, кто вовлечен. Даже после ее первоначального построения она может быть изменена для учета вновь задуманных критериев или критериев, которые изначально не считались важными; альтернативы также могут быть добавлены, удалены или изменены. [26]

Чтобы лучше понять иерархии AHP, рассмотрим задачу принятия решения с целью, которую необходимо достичь, тремя альтернативными способами достижения цели и четырьмя критериями, по которым необходимо оценивать альтернативы.

Такую иерархию можно визуализировать в виде диаграммы, подобной той, что представлена ​​ниже, с целью наверху, тремя альтернативами внизу и четырьмя критериями между ними. Существуют полезные термины для описания частей таких диаграмм: Каждый блок называется узлом. Узел, который соединен с одним или несколькими узлами на уровне ниже, называется родительским узлом. Узлы, с которыми он соединен таким образом, называются его дочерними.

Применяя эти определения к диаграмме ниже, цель является родителем четырех критериев, а четыре критерия являются дочерними элементами цели. Каждый критерий является родителем трех Альтернатив. Обратите внимание, что есть только три Альтернативы, но на диаграмме каждая из них повторяется под каждым из своих родителей.

Простая иерархия AHP. Существует три Альтернативы для достижения Цели и четыре Критерия, которые следует использовать при выборе между ними.

Чтобы уменьшить размер требуемого чертежа, принято представлять иерархии AHP, как показано на схеме ниже, с одним узлом для каждой альтернативы и несколькими линиями, соединяющими альтернативы и критерии, которые к ним применяются. Чтобы избежать беспорядка, эти линии иногда опускаются или их количество сокращается. Независимо от любых таких упрощений на схеме, в фактической иерархии каждый критерий индивидуально связан с альтернативами. Линии можно рассматривать как направленные вниз от родителя на одном уровне к его потомкам на уровне ниже.

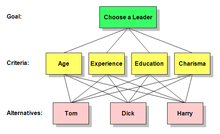
Иерархия AHP для выбора лидера. Есть одна цель, три кандидата и четыре критерия для выбора среди них.

Оцените иерархию

После построения иерархии участники анализируют ее с помощью серии парных сравнений, которые выводят числовые шкалы измерения для узлов. Критерии попарно сравниваются с целью по важности. Альтернативы попарно сравниваются с каждым из критериев по предпочтению. Сравнения обрабатываются математически, и приоритеты выводятся для каждого узла.

Рассмотрим пример «Выберите лидера» выше. Важной задачей лиц, принимающих решения, является определение веса, который следует придать каждому критерию при выборе лидера. Другая важная задача — определение веса, который следует придать каждому кандидату в отношении каждого из критериев. AHP не только позволяет им это сделать, но и позволяет им присвоить значимое и объективное числовое значение каждому из четырех критериев.

В отличие от большинства опросов, в которых используется пятибалльная шкала Лайкерта , опросник AHP имеет шкалу 9 к 1 к 9. [29]

Установить приоритеты

В этом разделе объясняются приоритеты, показывается, как они устанавливаются, и приводится простой пример.

Приоритеты определены и объяснены

Приоритеты — это числа, связанные с узлами иерархии AHP. Они представляют относительные веса узлов в любой группе.

Как и вероятности, приоритеты — это абсолютные числа от нуля до единицы, без единиц измерения или измерений. Узел с приоритетом .200 имеет в два раза больший вес в достижении цели, чем узел с приоритетом .100, в десять раз больший вес узла с приоритетом .020 и так далее. В зависимости от рассматриваемой проблемы «вес» может относиться к важности, предпочтению, вероятности или любому фактору, который учитывается лицами, принимающими решения.

Приоритеты распределены по иерархии в соответствии с ее архитектурой, а их значения зависят от информации, введенной пользователями процесса. Приоритеты Цели, Критериев и Альтернатив тесно связаны, но должны рассматриваться отдельно.

По определению приоритет Цели равен 1.000. Приоритеты альтернатив всегда в сумме составляют 1.000. Все может усложниться с несколькими уровнями Критериев, но если есть только один уровень, их приоритеты также в сумме составляют 1.000. Все это проиллюстрировано приоритетами в примере ниже.

Простая иерархия AHP с соответствующими приоритетами по умолчанию

Обратите внимание, что приоритеты на каждом уровне примера — цель, критерии и альтернативы — в сумме дают 1,000.

Показанные приоритеты — это те, которые существуют до ввода какой-либо информации о весах критериев или альтернатив, поэтому приоритеты на каждом уровне все равны. Они называются приоритетами иерархии по умолчанию. Если бы к этой иерархии был добавлен пятый Критерий, приоритет по умолчанию для каждого Критерия был бы .200. Если бы было только две Альтернативы, каждая имела бы приоритет по умолчанию .500.

Две дополнительные концепции применяются, когда иерархия имеет более одного уровня критериев: локальные приоритеты и глобальные приоритеты. Рассмотрим иерархию, показанную ниже, которая имеет несколько Подкритериев под каждым Критерием.

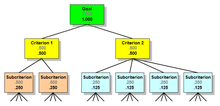
Более сложная иерархия AHP с локальными и глобальными приоритетами по умолчанию. В целях ясности альтернативы решений не показаны на диаграмме.

Локальные приоритеты, показанные серым цветом, представляют относительные веса узлов в группе сестринских узлов по отношению к их родителю. Локальные приоритеты каждой группы Criteria и их сестринских Subcriteria в сумме составляют 1.000. Глобальные приоритеты, показанные черным цветом, получаются путем умножения локальных приоритетов сестринских узлов на глобальный приоритет их родителя. Глобальные приоритеты для всех подкритериев на уровне в сумме составляют 1.000.

Правило таково: в иерархии глобальные приоритеты дочерних узлов всегда добавляются к глобальному приоритету их родителя. В группе дочерних узлов локальные приоритеты добавляются к 1.000.

До сих пор мы рассматривали только приоритеты по умолчанию. По мере продвижения процесса аналитической иерархии приоритеты будут меняться относительно своих значений по умолчанию, поскольку лица, принимающие решения, вводят информацию о важности различных узлов. Они делают это, выполняя ряд парных сравнений.

Практические примеры

Опытные практики знают, что лучший способ понять AHP — это проработать случаи и примеры. Два подробных примера , специально разработанных как примеры углубленного обучения, приводятся в качестве приложений к этой статье:

Некоторые книги по AHP содержат практические примеры его использования, хотя они обычно не предназначены для пошагового обучения. [26] [31] Одна из них содержит несколько расширенных примеров, а также около 400 иерархий AHP, кратко описанных и проиллюстрированных рисунками. [28] Многие примеры обсуждаются, в основном для профессиональной аудитории, в статьях, опубликованных Международным симпозиумом по процессу аналитической иерархии . [32] [33] [34] [35] [36]

Критика

AHP включен в большинство учебников по исследованию операций и науке управления и преподается во многих университетах; он широко используется в организациях, которые тщательно исследовали его теоретические основы. [1] У метода есть свои критики. [8] В начале 1990-х годов серия дебатов между критиками и сторонниками AHP была опубликована в Management Science [37] [38] [39] [40] и The Journal of the Operational Research Society, [41] [42] [43] двух престижных журналах, где Саати и его коллеги имели значительное влияние. Эти дебаты, похоже, были урегулированы в пользу AHP:

В статье 1997 года были рассмотрены возможные недостатки в вербальной (по сравнению с числовой) шкале, часто используемой в парных сравнениях AHP. [45] В другой статье того же года утверждалось, что безобидные изменения в модели AHP могут внести порядок там, где его нет. [46] В статье 2006 года было обнаружено, что добавление критериев, по которым все альтернативы работают одинаково, может изменить приоритеты альтернатив. [47]

В 2021 году первая комплексная оценка AHP была опубликована в книге, написанной двумя учеными из Технического университета Валенсии и Политехнического университета Картахены , и изданной Springer Nature . На основе эмпирического исследования и объективных показаний 101 исследователя исследование обнаружило не менее 30 недостатков в AHP и сочло его непригодным для решения сложных задач, а в некоторых ситуациях даже для решения небольших задач. [48]

Изменение ранга

Принятие решений подразумевает ранжирование альтернатив с точки зрения критериев или атрибутов этих альтернатив. Аксиома некоторых теорий принятия решений заключается в том, что когда к проблеме принятия решения добавляются новые альтернативы, ранжирование старых альтернатив не должно меняться — что « перестановка рангов » не должна происходить.

Существует две школы мысли об изменении ранга. Одна утверждает, что новые альтернативы, не вводящие дополнительных атрибутов, не должны вызывать изменение ранга ни при каких обстоятельствах. Другая утверждает, что существуют некоторые ситуации, в которых изменение ранга можно обоснованно ожидать. Первоначальная формулировка AHP допускала изменение ранга. В 1993 году Форман [49] представил второй режим синтеза AHP, названный идеальным режимом синтеза, для решения ситуаций выбора, в которых добавление или удаление «нерелевантной» альтернативы не должно и не будет вызывать изменение рангов существующих альтернатив. Текущая версия AHP может вместить обе эти школы — его идеальный режим сохраняет ранг, в то время как его распределительный режим позволяет изменять ранги. Любой из режимов выбирается в соответствии с решаемой задачей.

Инверсия ранга и AHP подробно обсуждаются в статье 2001 года в Operations Research [1], а также в главе под названием Rank Preservation and Reversal в текущей базовой книге по AHP. [31] В последней представлены опубликованные примеры инверсии ранга из-за добавления копий и почти копий альтернативы, из-за нетранзитивности правил принятия решений, из-за добавления фантомных и ложных альтернатив и из-за явления переключения в функциях полезности. В ней также обсуждаются распределительные и идеальные режимы AHP.

В 2014 году была обнаружена новая форма изменения ранга AHP [50] , при которой AHP изменяет порядок ранга, исключая нерелевантные данные, то есть данные, которые не различают альтернативы.

Существуют различные типы перестановок рангов. Кроме того, другие методы, помимо AHP, могут демонстрировать такие перестановки рангов. Более подробное обсуждение перестановок рангов с помощью AHP и других методов MCDM представлено на странице перестановок рангов при принятии решений .

Немонотонность некоторых методов извлечения веса

В матрице сравнения можно заменить суждение на менее благоприятное суждение, а затем проверить, становится ли указание нового приоритета менее благоприятным, чем исходный приоритет. В контексте турнирных матриц Оскар Перрон [51] доказал , что метод главного правого собственного вектора не является монотонным. Такое поведение можно продемонстрировать и для обратных матриц nxn, где n > 3. Альтернативные подходы обсуждаются в другом месте. [52] [53] [54] [55]

Смотрите также

Ссылки

  1. ^ abcde Форман, Эрнест Х.; Сол И. Гасс (июль 2001 г.). «Процесс аналитической иерархии — изложение». Исследование операций . 49 (4): 469–487. doi :10.1287/opre.49.4.469.11231.
  2. ^ Фабианек, Пол; Кристиан Вилл; Стефани Вольф; Райнхард Мадленер (2020). «Зеленый и региональный? Многокритериальная структура оценки для обеспечения зеленой электроэнергии для электромобилей в Германии». Исследования транспорта, часть D. 87 ( D): 102504. doi :10.1016/j.trd.2020.102504.
  3. ^ ab Saaty, Thomas L. ; Peniwati, Kirti (2008). Групповое принятие решений: выявление и согласование различий . Питтсбург, Пенсильвания: RWS Publications. ISBN 978-1-888603-08-8.
  4. ^ Сараджоглу, БО (2013). «Выбор мест для промышленных инвестиций в генеральных планах стран». Европейский журнал промышленной инженерии . 7 (4): 416–441. doi :10.1504/EJIE.2013.055016.
  5. ^ Saaty, Thomas L. (июнь 2008 г.). «Относительное измерение и его обобщение в принятии решений: почему парные сравнения играют центральную роль в математике для измерения неосязаемых факторов – аналитический иерархический/сетевой процесс» (PDF) . Обзор Королевской академии точных, физических и естественных наук, серия A: Математика . 102 (2): 251–318. CiteSeerX 10.1.1.455.3274 . doi :10.1007/bf03191825. S2CID  42215574 . Получено 22.12.2008 . 
  6. ^ ab Bhushan, Navneet; Kanwal Rai (январь 2004). Стратегическое принятие решений: применение аналитической иерархии процесса. Лондон: Springer-Verlag. ISBN 978-1-85233-756-8.
  7. ^ Berrittella, M.; A. Certa; M. Enea; P. Zito (январь 2007 г.). "Процесс аналитической иерархии для оценки транспортной политики по сокращению последствий изменения климата" (PDF) . Fondazione Eni Enrico Mattei (Милан). Архивировано из оригинала (PDF) 2016-03-04 . Получено 2011-02-16 .
  8. ^ ab McCaffrey, James (июнь 2005 г.). "Test Run: The Analytic Hierarchy Process". Журнал MSDN . Получено 21 августа 2007 г.
  9. ^ Грандзол, Джон Ричард (август 2005 г.). «Улучшение процесса отбора преподавателей в высшем образовании: случай аналитического иерархического процесса» (PDF) . IR Applications . 6 . Архивировано из оригинала (PDF) 2007-10-30 . Получено 2007-08-21 .
  10. ^ Atthirawong, Walailak; Bart McCarthy (сентябрь 2002 г.). «Применение аналитического иерархического процесса к принятию решений о международном размещении». В Gregory, Mike (ред.). Труды 7-го ежегодного Кембриджского международного производственного симпозиума: реструктуризация глобального производства . Кембридж, Англия: Кембриджский университет. стр. 1–18. Архивировано из оригинала (PDF) 22.03.2016 . Получено 23.10.2007 .
  11. ^ Дей, Прасанта Кумар (ноябрь 2003 г.). «Процесс аналитической иерархии анализирует риск эксплуатации магистральных нефтепроводов в Индии». Обзор природных опасностей . 4 (4): 213–221. doi :10.1061/(ASCE)1527-6988(2003)4:4(213) . Получено 20 августа 2007 г.
  12. ^ de Steiguer, JE; Jennifer Duberstein; Vicente Lopes (октябрь 2003 г.). «Процесс аналитической иерархии как средство комплексного управления водоразделами» (PDF) . В Renard, Kenneth G. (ред.). Первая межведомственная конференция по исследованию водоразделов . Бенсон, Аризона: Министерство сельского хозяйства США, Служба сельскохозяйственных исследований. стр. 736–740.
  13. ^ ab Wu, Guangdong; Duan, Kaifeng; Zuo, Jian; Zhao, Xianbo; Tang, Daizhong (13 апреля 2017 г.). «Комплексная оценка устойчивости государственного арендного жилищного сообщества на основе гибридного метода AHP-энтропийного веса и облачной модели». Sustainability . 9 (4): 603. doi : 10.3390/su9040603 . ISSN  2071-1050. OCLC  7016685474.
  14. ^ Салем, О., Салман, Б. и Гораи, С. (2017). Ускорение строительства автодорожных мостов с использованием альтернативных технологий и методов закупок. Транспорт, 33(2), 567-579. https://doi.org/10.3846/16484142.2017.1300942
  15. ^ Липперт, Барбара К.; Стивен Ф. Вебер (октябрь 1995 г.). "HIST 1.0; Программное обеспечение поддержки принятия решений для оценки зданий по исторической значимости" (PDF) . Национальный институт стандартов и технологий, NIST IR 5683. Получено 20 августа 2007 г.
  16. ^ Ларсон, Чарльз Д.; Эрнест Х. Форман (январь 2007 г.). «Применение процесса аналитической иерархии для выбора области действия проекта для видеорегистрации и сбора данных о состоянии дорожного покрытия». Сборник докладов 86-го ежегодного собрания на CD-ROM . Исследовательский совет по транспорту национальных академий.
  17. ^ Дуань, Йе; Му, Хайлинь; Ли, Нань; Ли, Линьлинь; Сюэ, Чжаоцюань (2016). «Исследование комплексной оценки уровня развития низкоуглеродной экономики на основе метода AHP-энтропии: пример Даляня». Energy Procedia . 104 : 468–474. doi : 10.1016/j.egypro.2016.12.079 .
  18. ^ Drake, PR (1998). «Использование процесса аналитической иерархии в инженерном образовании» (PDF) . Международный журнал инженерного образования . 14 (3): 191–196. Архивировано из оригинала (PDF) 2007-11-28 . Получено 2007-08-20 .
  19. ^ Бодин, Лоуренс; Сол И. Гасс (январь 2004 г.). «Упражнения для обучения аналитическому иерархическому процессу». Труды INFORMS по образованию . 4 (2): 1–13. doi : 10.1287/ited.4.2.1 .
  20. ^ Hallowell, David L. (январь 2005 г.). "Analytical Hierarchy Process (AHP) – Getting Oriented". ISixSigma.com . Архивировано из оригинала 11 августа 2007 г. . Получено 21 августа 2007 г.
  21. ^ "Analytic Hierarchy Process (AHP)". QFD Institute . Архивировано из оригинала 22 августа 2007 года . Получено 21 августа 2007 года .
  22. ^ "Процесс аналитической иерархии: обзор". TheQualityPortal.com . Архивировано из оригинала 29 августа 2007 . Получено 2007-08-21 .
  23. ^ "Имена и документы участников, ISAHP 2005, Гонолулу, Гавайи". Июль 2005. Архивировано из оригинала 29-02-2008 . Получено 22-08-2007 .
  24. ^ Гарути, Клаудио, ред. (2007). "Имена участников и доклады". Труды 9-го Международного симпозиума по процессу анализа иерархий . Винья-дель-Мар, Чили: ISAHP. Архивировано из оригинала 2011-07-26 . Получено 2011-01-05 .
  25. ^ Saaty, Rozann, ed. (2009). «Имена участников и доклады». Труды 10-го Международного симпозиума по аналитической иерархии/сетевому процессу . Питтсбург, Пенсильвания: ISAHP.
  26. ^ abcde Saaty, Thomas L. (2008). Принятие решений для лидеров: аналитический иерархический процесс принятия решений в сложном мире . Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-8-6.(Эта книга является основным источником для разделов, в которых она цитируется.)
  27. ^ Саати, Томас Л. (2010). Principia Mathematica Decernendi: Математические принципы принятия решений . Питтсбург, Пенсильвания: RWS Publications. ISBN 978-1-888603-10-1.
  28. ^ ab Saaty, Thomas L. ; Ernest H. Forman (1992). Иерархон: Словарь иерархий . Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-5-5.496 страниц, спиральный переплет. Каждая запись включает описание и схему модели AHP; модели сгруппированы по категориям: образовательные, правительственная/государственная политика, правительственная/общественная/стратегия, здравоохранение, военные, некоммерческие, личные, планирование, политические и т. д.
  29. ^ Ли, Рита Йи Ман; Чау, Квонг Винг; Цзэн, Фрэнки Фаньцзе (2019). «Ранжирование рисков для существующих и новых строительных работ». Устойчивость . 11 (10): 2863. doi : 10.3390/su11102863 .
  30. ^ Перес-Родригес, Фернандо; Рохо-Альборека, Альберто (2012-01-12). «Применение AHP в лесном хозяйстве с использованием программного обеспечения MPC©». Forest Systems . 21 (3): 418–425. doi : 10.5424/fs/2012213-02641 . hdl : 10347/21679 .
  31. ^ ab Saaty, Thomas L. (2001). Основы принятия решений и теории приоритетов . Питтсбург, Пенсильвания: RWS Publications. ISBN 978-0-9620317-6-2.
  32. ^ "Труды 6-го Международного симпозиума по AHP". Веб-сайт ISAHP . ISAHP. Август 2001 г. Получено 2009-04-03 .
  33. ^ "Труды 7-го Международного симпозиума по AHP". Веб-сайт ISAHP . ISAHP. Август 2003 г. Получено 2009-04-03 .
  34. ^ "Труды 8-го Международного симпозиума по AHP". Веб-сайт ISAHP . ISAHP. Август 2005 г. Получено 2009-04-03 .
  35. ^ "Труды 9-го Международного симпозиума по AHP". Веб-сайт ISAHP . ISAHP. Август 2007 г. Получено 2009-04-03 .
  36. ^ "Труды 10-го Международного симпозиума по AHP". Веб-сайт ISAHP . ISAHP. Август 2009. Получено 2011-01-05 .
  37. ^ Дайер, Дж. С. (1990): Замечания о процессе аналитической иерархии. В: Наука управления, 36 (3), С. 249-258.
  38. ^ М. В. Михалевич «Замечания о споре Дайера-Саати» Кибернетика и системный анализ, том 30, номер 1 / январь 1994 г.
  39. ^ Патрик Т. Харкер, Луис Г. Варгас, «Ответ на «Замечания о процессе аналитической иерархии» Дж. С. Дайера», Management Science, т. 36, № 3 (март 1990 г.), стр. 269-273
  40. ^ Дайер, Дж. С. (1990b), «Разъяснение «Замечаний о процессе аналитической иерархии»», Наука управления, т. 36, № 3, стр. 274-5.
  41. ^ Холдер, Р.Д., Некоторые комментарии к процессу аналитической иерархии, Журнал Общества операционных исследований, 1990, 41, 11 1073-1076.
  42. ^ Томас Л. Саати «Ответ на комментарии Холдера о процессе аналитической иерархии» Журнал общества операционных исследований, т. 42, № 10 (октябрь 1991 г.), стр. 909-914
  43. ^ RD Holder "Ответ на комментарии Holder's о процессе аналитической иерархии: ответ на ответ" Журнал общества операционных исследований, том 42, № 10 (октябрь 1991 г.), стр. 914-918
  44. ^ Институт исследования операций и управленческих наук *В 2008 году Томас Л. Саати получил премию INFORMS Impact Prize за разработку процесса аналитической иерархии.
  45. ^ Мари А. Пёйхёнен, Раймо П. Хямяляйнен, Ахти А. Сало «Эксперимент по численному моделированию словесных соотношений» Журнал многокритериального анализа решений, том 6, № 1, стр. 1-10, 1997
  46. ^ Стэн Шенкерман «Создание несуществующего порядка с помощью аналитической иерархии», Decision Sciences, весна 1997 г.
  47. ^ Перес и др. «Еще один потенциальный недостаток AHP» TOP: Официальный журнал Испанского общества статистики и исследования операций, том 14, номер 1 / июнь 2006 г., Springer Berlin/Heidelberg
  48. ^ Мунье, Нольберто (2021). Использование и ограничения метода AHP. Нематематический и рациональный анализ. Менеджмент для профессионалов. Швейцария: Springer Nature . doi : 10.1007/978-3-030-60392-2. ISBN 978-3-030-60392-2. S2CID  241759250.
  49. ^ Форман, Эрнест Х., «Идеальные и распределенные режимы синтеза для процесса аналитической иерархии», представленный на Международной федерации исследований операций, Лиссабон, Португалия, июль 1993 г.
  50. ^ Арройо, П.; Томмелейн, И.Д.; Баллард, Г. (январь 2015 г.). «Сравнение AHP и CBA как методов принятия решений для решения проблемы выбора в детальном проектировании». Журнал строительной инженерии и менеджмента . 141 (1): 04014063. doi :10.1061/(ASCE)CO.1943-7862.0000915.
  51. ^ Ландау, Э. (1914). " Über Preisverteilung bei Spielturnieren. Архивировано 13 марта 2020 г. в Wayback Machine . Zeitschrift für Mathematik und Physik , 63 группа (1914), стр. 192.
  52. ^ Цермело, Э. (1928). Die Berechnung der Turnier-Ergebnisse als ein Maximumproblem der Wahrscheinlichkeitsrechnung , Mathematische Zeitschrift 29, 1929, S. 436–460
  53. ^ Хассе, М (1961). «Über die Behandlunggraphentheoretischer Issuee unter Verwendung der Matrizenrechnung». Висс. Зейт. Тех. унив. Дрезден . 10 : 1313–6.
  54. ^ Ramanujacharyulu, C (1964). «Анализ предпочтительных экспериментов». Psychometrika . 29 (3): 257–261. doi :10.1007/bf02289722. S2CID  121033891. Архивировано из оригинала 2013-12-16.
  55. ^ Салавати, А., Хагшенас, Х., Гадирифараз, Б., Лагхаи, Дж. и Эфтехари, Г. (2016). Применение AHP и кластерных подходов для принятия решений в сфере общественного транспорта: пример города Исфахан. Журнал общественного транспорта, 19(4), 3.

Дальнейшее чтение

Внешние ссылки

На Викискладе есть медиафайлы по теме «Процесс анализа иерархии» .