Разложение по сингулярным значениям

Разложение матрицы

Иллюстрация сингулярного разложения UΣV ^⁎ вещественной матрицы M 2×2 .

• Вверху: действие M , обозначенное его влиянием на единичный круг D и два канонических единичных вектора e ₁ и e ₂ .
• Слева: действие V ^⁎ , вращения, на D , e ₁ и e ₂ .
• Внизу: действие Σ , масштабирование сингулярными значениями σ ₁ по горизонтали и σ ₂ по вертикали.
• Справа: действие U , еще одно вращение.

В линейной алгебре разложение по сингулярным значениям ( SVD ) представляет собой факторизацию вещественной или комплексной матрицы в вращение с последующим изменением масштаба и последующим вращением. Он обобщает собственное разложение квадратной нормальной матрицы с ортонормированным собственным базисом на любую матрицу. Это связано с полярным разложением . ${\displaystyle \ m\times n\ }$

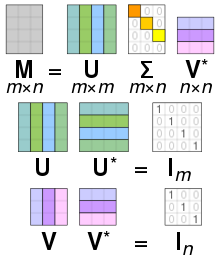
В частности, разложение по сингулярным значениям комплексной матрицы M представляет собой факторизацию формы , где U — комплексная унитарная матрица , — прямоугольная диагональная матрица с неотрицательными действительными числами на диагонали, V — комплексная унитарная матрица, и — сопряженное транспонирование V . Такое разложение всегда существует для любой комплексной матрицы. Если M вещественное, то можно гарантировать, что U и V будут вещественными ортогональными матрицами; в таких контекстах часто обозначается СВД . ${\displaystyle \ m\times n\ }$ ${\displaystyle \ \mathbf {M} =\mathbf {U\Sigma V^{*}} \ ,}$ ${\displaystyle \ m\times m\ }$ ${\displaystyle \ \mathbf {\Sigma } \ }$ ${\displaystyle \ m\times n\ }$ ${\displaystyle n\times n}$ ${\displaystyle \ \mathbf {V^{*}} \ }$ ${\displaystyle \ \mathbf {U\Sigma V} ^{\operatorname {T} }}$

Диагональные элементы однозначно определяются M и известны как сингулярные значения M . Количество ненулевых сингулярных значений равно рангу M . Столбцы U и столбцы V называются левосингулярными векторами и правосингулярными векторами M соответственно. Они образуют два набора ортонормированных базисов u ₁ , ..., um и v ₁ , ..., v _{n , и если они} отсортированы так, что сингулярные значения с нулевым значением все находятся в столбцах с наибольшим номером (или строки), разложение по сингулярным значениям можно записать как где - ранг M . ${\displaystyle \ \sigma _{i}=\Sigma _{ii}\ }$ ${\displaystyle \ \mathbf {\Sigma } \ }$   ${\displaystyle \ \sigma _{i}\ }$ ${\displaystyle \ \mathbf {M} =\sum _{i=1}^{r}\sigma _{i}\mathbf {u} _{i}\mathbf {v} _{i}^{*}\ ,}$ ${\displaystyle \ r\leq \min\{m,n\}\ }$

СВД не уникальна. Всегда можно выбрать разложение так, чтобы сингулярные значения располагались в порядке убывания. В этом случае (но не U и V ) однозначно определяется M. ${\displaystyle \Sigma _{ii}}$ ${\displaystyle \mathbf {\Sigma } }$

Этот термин иногда относится к компактному SVD , аналогичному разложению , в котором есть квадратная диагональ размера , где - ранг M , и имеет только ненулевые сингулярные значения. В этом варианте U — полуунитарная матрица и — полуунитарная матрица такая, что ${\displaystyle \ \mathbf {M} =\mathbf {U\Sigma V^{*}} \ }$ ${\displaystyle \ \mathbf {\Sigma } \ }$ ${\displaystyle r\times r}$ ${\displaystyle \ r\leq \min\{m,n\}\ }$ ${\displaystyle m\times r}$ ${\displaystyle \ \mathbf {V} \ }$ ${\displaystyle n\times r}$ ${\displaystyle \ \mathbf {U^{*}U} =\mathbf {V^{*}V} =\mathbf {I} _{r}\ .}$

Математические приложения SVD включают вычисление псевдообратной матрицы , аппроксимацию и определение ранга, диапазона и нулевого пространства матрицы. SVD также чрезвычайно полезен во всех областях науки, техники и статистики , таких как обработка сигналов , аппроксимация данных методом наименьших квадратов и управление процессами .

Интуитивные интерпретации

Анимированная иллюстрация SVD двумерной реальной матрицы сдвига M . Сначала мы видим единичный круг синим цветом вместе с двумя каноническими единичными векторами . Затем мы видим действие M , которое искажает диск в эллипс . SVD разлагает M на три простых преобразования: начальное вращение V ^⁎ , масштабирование по осям координат и окончательное вращение U . Длины σ1 и σ2 полуосей эллипса являются _{сингулярными} значениями M _, а именно Σ1,1 и _{Σ2,2 .} _ _ ${\displaystyle \mathbf {\Sigma } }$

Визуализация умножения матриц при разложении по сингулярным значениям

Вращение, масштабирование координат и отражение

В особом случае, когда M представляет собой вещественную квадратную матрицу размера m × m , матрицы U и V ^также могут быть выбраны действительными матрицами размера m × m . В этом случае «унитарный» — это то же самое, что « ортогональный ». Затем, интерпретируя обе унитарные матрицы , а также диагональную матрицу, обозначенную здесь как A , как линейное преобразование x ↦ Ax пространства R ^m , матрицы U и V ^⁎ представляют собой вращения или отражение пространства, а представляют масштабирование каждую координату x _i на коэффициент σ _i . Таким образом, разложение SVD разбивает любое линейное преобразование R ^m на композицию трех геометрических преобразований : поворот или отражение ( V ^⁎ ), за которым следует покоординатное масштабирование ( ), за которым следует еще одно вращение или отражение ( U ). . ${\displaystyle \mathbf {\Sigma } }$ ${\displaystyle \mathbf {\Sigma } }$

В частности, если M имеет положительный определитель, то U и V ^⁎ могут быть выбраны как оба вращения с отражениями, или как оба вращения без отражений. ^{[ нужна цитата ]} Если определитель отрицательный, ровно один из них будет иметь отражение. Если определитель равен нулю, каждый из них может быть независимо выбран как любой тип.

Если матрица M вещественная, но не квадратная, а именно m × n с m ≠ n , ее можно интерпретировать как линейное преобразование из R ⁿ в R ^m . Тогда U и V ^⁎ можно выбрать в качестве вращений/отражений R ^m и R ⁿ соответственно; и , помимо масштабирования первых координат, также расширяет вектор нулями, т.е. удаляет конечные координаты, чтобы превратить R ⁿ в R ^m . ${\displaystyle \mathbf {\Sigma } }$ ${\displaystyle \min\{m,n\}}$

Сингулярные значения как полуоси эллипса или эллипсоида

Как показано на рисунке, сингулярные значения можно интерпретировать как величину полуосей эллипса в 2D. Эту концепцию можно обобщить на n -мерное евклидово пространство , при этом сингулярные значения любой квадратной матрицы размера n × n рассматриваются как величина полуоси n -мерного эллипсоида . Аналогично, сингулярные значения любой матрицы размера m × n можно рассматривать как величину полуоси n -мерного эллипсоида в m -мерном пространстве, например, как эллипс в (наклоненной) двумерной плоскости в трехмерном пространстве. Сингулярные значения кодируют величину полуоси, а сингулярные векторы кодируют направление. Более подробную информацию смотрите ниже.

Столбцы U и V являются ортонормированными базисами.

Поскольку U и V ^⁎ унитарны, столбцы каждого из них образуют набор ортонормированных векторов , которые можно рассматривать как базисные векторы . Матрица M отображает базисный вектор V _i в растянутый единичный вектор σ _i U _i . По определению унитарной матрицы то же самое верно для их сопряженных транспонирований U ^⁎ и V , за исключением того, что теряется геометрическая интерпретация сингулярных значений как растяжений. Короче говоря, столбцы U , U ^⁎ , V и V ^⁎ являются ортонормированными базисами . Когда положительно -полуопределенная эрмитова матрица , U и V оба равны унитарной матрице, используемой для диагонализации . Однако, когда он не является положительно-полуопределенным и эрмитовым, но все же диагонализируем , его собственное разложение и разложение по сингулярным значениям различны. ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} }$

Геометрический смысл

Поскольку U и V унитарны, мы знаем, что столбцы U ₁ , ..., U _m из U дают ортонормированный базис K ^m , а столбцы V ₁ , ..., V _n из V дают ортонормированный базис K ⁿ (относительно стандартных скалярных произведений на этих пространствах).

Линейное преобразование

${\displaystyle T\colon \left\{{\begin{aligned}K^{n}&\to K^{m}\\x&\mapsto \mathbf {M} x\end{aligned}}\right.}$

имеет особенно простое описание относительно этих ортонормированных базисов: мы имеем

${\displaystyle T(\mathbf {V} _{i})=\sigma _{i}\mathbf {U} _{i},\qquad i=1,\ldots ,\min(m,n),}$

где σ _{i i} -я диагональная запись , и T ( V _i ) = 0 для i > min( m , n ) . ${\displaystyle \mathbf {\Sigma } }$

^{Таким образом , геометрическое содержание} теоремы SVD можно резюмировать следующим образом: для любого линейного отображения T  : Kn → Km можно найти ортонормированные базисы Kn и Km такие, что T отображает i ^- й базисный вектор Kn ^в неотрицательное кратное i -го базисного вектора K ^m и переводит оставшиеся базисные векторы в ноль. Таким образом , относительно этих базисов карта T представляется диагональной матрицей с неотрицательными действительными диагональными элементами.

Чтобы получить более наглядное представление о сингулярных значениях и факторизации SVD – по крайней мере, при работе с реальными векторными пространствами – рассмотрим сферу S радиуса один в R ⁿ . Линейное отображение T отображает эту сферу ^на эллипсоид в Rm . Ненулевые сингулярные значения — это просто длины полуосей этого эллипсоида. Особенно когда n = m и все сингулярные значения различны и ненулевые, SVD линейного отображения T можно легко проанализировать как последовательность трех последовательных ходов: рассмотрим эллипсоид T ( S ) и, в частности, его оси; затем рассмотрим направления в R ⁿ , посланные T на эти оси. Эти направления оказываются взаимно ортогональными. Сначала примените изометрию V ^⁎ , отправив эти направления к осям координат R ⁿ . На втором ходу примените эндоморфизм D , диагонализованный вдоль координатных осей и растягивающий или сжимающий в каждом направлении, используя длины полуосей T ( S ) в качестве коэффициентов растяжения. Затем композиция D ∘ V ^⁎ отправляет единичную сферу на эллипсоид, изометричный T ( S ) . Чтобы определить третий и последний ход, примените изометрию U к этому эллипсоиду, чтобы получить T ( S ) . Как легко проверить, композиция U ∘ D ∘ V ^⁎ совпадает с T .

Пример

Рассмотрим матрицу 4 × 5

${\displaystyle \mathbf {M} ={\begin{bmatrix}1&0&0&0&2\\0&0&3&0&0\\0&0&0&0&0\\0&2&0&0&0\end{bmatrix}}}$

Разложение этой матрицы по сингулярным значениям имеет вид UΣV ^⁎

${\displaystyle {\begin{aligned}\mathbf {U} &={\begin{bmatrix}\color {Green}0&\color {Blue}-1&\color {Cyan}0&\color {Emerald}0\\\color {Green}-1&\color {Blue}0&\color {Cyan}0&\color {Emerald}0\\\color {Green}0&\color {Blue}0&\color {Cyan}0&\color {Emerald}-1\\\color {Green}0&\color {Blue}0&\color {Cyan}-1&\color {Emerald}0\end{bmatrix}}\\[6pt]{\boldsymbol {\Sigma }}&={\begin{bmatrix}3&0&0&0&\color {Gray}{\mathit {0}}\\0&{\sqrt {5}}&0&0&\color {Gray}{\mathit {0}}\\0&0&2&0&\color {Gray}{\mathit {0}}\\0&0&0&\color {Red}\mathbf {0} &\color {Gray}{\mathit {0}}\end{bmatrix}}\\[6pt]\mathbf {V} ^{*}&={\begin{bmatrix}\color {Violet}0&\color {Violet}0&\color {Violet}-1&\color {Violet}0&\color {Violet}0\\\color {Plum}-{\sqrt {0.2}}&\color {Plum}0&\color {Plum}0&\color {Plum}0&\color {Plum}-{\sqrt {0.8}}\\\color {Magenta}0&\color {Magenta}-1&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0\\\color {Orchid}0&\color {Orchid}0&\color {Orchid}0&\color {Orchid}1&\color {Orchid}0\\\color {Purple}-{\sqrt {0.8}}&\color {Purple}0&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.2}}\end{bmatrix}}\end{aligned}}}$

Матрица масштабирования равна нулю за пределами диагонали (серый курсив), а один диагональный элемент равен нулю (красный жирный шрифт, светло-синий жирный шрифт в темном режиме). Кроме того, поскольку матрицы U и V ^⁎ унитарны , умножение на соответствующие им сопряженные транспонирования дает единичные матрицы , как показано ниже. В этом случае, поскольку U и V ^⁎ имеют действительные значения, каждая из них является ортогональной матрицей . ${\displaystyle \mathbf {\Sigma } }$

${\displaystyle {\begin{aligned}\mathbf {U} \mathbf {U} ^{*}&={\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}=\mathbf {I} _{4}\\[6pt]\mathbf {V} \mathbf {V} ^{*}&={\begin{bmatrix}1&0&0&0&0\\0&1&0&0&0\\0&0&1&0&0\\0&0&0&1&0\\0&0&0&0&1\end{bmatrix}}=\mathbf {I} _{5}\end{aligned}}}$

Это конкретное разложение по сингулярным значениям не уникально. Выбирая такое, что ${\displaystyle \mathbf {V} }$

${\displaystyle \mathbf {V} ^{*}={\begin{bmatrix}\color {Violet}0&\color {Violet}1&\color {Violet}0&\color {Violet}0&\color {Violet}0\\\color {Plum}0&\color {Plum}0&\color {Plum}1&\color {Plum}0&\color {Plum}0\\\color {Magenta}{\sqrt {0.2}}&\color {Magenta}0&\color {Magenta}0&\color {Magenta}0&\color {Magenta}{\sqrt {0.8}}\\\color {Orchid}{\sqrt {0.4}}&\color {Orchid}0&\color {Orchid}0&\color {Orchid}{\sqrt {0.5}}&\color {Orchid}-{\sqrt {0.1}}\\\color {Purple}-{\sqrt {0.4}}&\color {Purple}0&\color {Purple}0&\color {Purple}{\sqrt {0.5}}&\color {Purple}{\sqrt {0.1}}\end{bmatrix}}}$

также является допустимым разложением по сингулярным значениям.

СВД и спектральное разложение

Сингулярные значения, сингулярные векторы и их связь с SVD

Неотрицательное действительное число σ является сингулярным значением для M тогда и только тогда, когда существуют векторы единичной длины в K ^m и в K ⁿ такие, что ${\displaystyle \mathbf {u} }$ ${\displaystyle \mathbf {v} }$

$${\displaystyle \mathbf {Mv} =\sigma \mathbf {u} \,{\text{ and }}\mathbf {M} ^{*}\mathbf {u} =\sigma \mathbf {v} .}$$

левосингулярнымиправосингулярными векторамиσ ${\displaystyle \mathbf {u} }$ ${\displaystyle \mathbf {v} }$

В любом разложении по сингулярным значениям

$${\displaystyle \mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}}$$

Mp = min( m , n )UV ${\displaystyle \mathbf {\Sigma } }$

• Матрица M размера m × n имеет не более p различных сингулярных значений.
• Всегда возможно найти унитарный базис U для K ^m с подмножеством базисных векторов, охватывающим левосингулярные векторы каждого сингулярного значения M .
• Всегда возможно найти унитарный базис V для K ⁿ с подмножеством базисных векторов, охватывающим правосингулярные векторы каждого сингулярного значения M .

Сингулярное значение, для которого можно найти два левых (или правых) сингулярных вектора, линейно независимых, называется вырожденным . Если и - два левосингулярных вектора, которые оба соответствуют сингулярному значению σ, то любая нормализованная линейная комбинация этих двух векторов также является левосингулярным вектором, соответствующим сингулярному значению σ. Аналогичное утверждение справедливо и для правосингулярных векторов. Число независимых левых и правых сингулярных векторов совпадает, и эти сингулярные векторы появляются в одних и тех же столбцах U и V , соответствующих диагональным элементам всех с одинаковым значением σ . ${\displaystyle \mathbf {u} _{1}}$ ${\displaystyle \mathbf {u} _{2}}$ ${\displaystyle \mathbf {\Sigma } }$

В качестве исключения, левый и правый сингулярные векторы сингулярного значения 0 содержат все единичные векторы в коядре и ядре соответственно M , которые по теореме о ранге-нулевости не могут быть одинаковой размерности, если m ≠ n . Даже если все сингулярные значения отличны от нуля, если m > n , то коядро нетривиально, и в этом случае U дополняется m - n ортогональными векторами из коядра. И наоборот, если m < n , то V дополняется n - m ортогональными векторами из ядра. Однако если сингулярное значение 0 существует, дополнительные столбцы U или V уже появляются как левые или право-сингулярные векторы.

Невырожденные сингулярные значения всегда имеют единственные лево- и право-сингулярные векторы с точностью до умножения на единичный фазовый множитель e ^{i φ} (для реального случая с точностью до знака). Следовательно, если все сингулярные значения квадратной матрицы M невырождены и ненулевые, то ее сингулярное разложение однозначно, вплоть до умножения столбца U на единичный фазовый множитель и одновременного умножения соответствующего столбца матрицы M. V на тот же единичный фазовый коэффициент. В общем, SVD уникален с точностью до произвольных унитарных преобразований, равномерно применяемых к векторам-столбцам U и V , охватывающим подпространства каждого сингулярного значения, а также с точностью до произвольных унитарных преобразований векторов U и V , охватывающих ядро ​​и коядро соответственно. , М. _

Связь с разложением собственных значений

Разложение по сингулярным значениям является очень общим в том смысле, что его можно применять к любой матрице размера m × n , тогда как разложение по собственным значениям можно применять только к квадратам диагонализируемых матриц . Тем не менее, эти два разложения связаны.

Если M имеет SVD , выполняются следующие два соотношения: ${\displaystyle \mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}}$

$${\displaystyle {\begin{aligned}\mathbf {M} ^{*}\mathbf {M} &=\mathbf {V} {\boldsymbol {\Sigma }}^{*}\mathbf {U} ^{*}\,\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}=\mathbf {V} ({\boldsymbol {\Sigma }}^{*}{\boldsymbol {\Sigma }})\mathbf {V} ^{*}\\\mathbf {M} \mathbf {M} ^{*}&=\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}\,\mathbf {V} {\boldsymbol {\Sigma }}^{*}\mathbf {U} ^{*}=\mathbf {U} ({\boldsymbol {\Sigma }}{\boldsymbol {\Sigma }}^{*})\mathbf {U} ^{*}\end{aligned}}}$$

• Столбцы V (называемые право-сингулярными векторами) являются собственными векторами M ^⁎ M .
• Столбцы U (называемые левосингулярными векторами) являются собственными векторами MM ^⁎ .
• Ненулевые элементы (ненулевые сингулярные значения) являются квадратными корнями ненулевых собственных значений M ^⁎ M или MM ^⁎ . ${\displaystyle \mathbf {\Sigma } }$

В частном случае, когда M является нормальной матрицей и, следовательно, также находится в квадрате, спектральная теорема гарантирует, что ее можно унитарно диагонализировать с использованием базиса собственных векторов и, таким образом, разложить, как для некоторой унитарной матрицы U и диагональной матрицы D с комплексными элементами σ _i по диагонали. Когда M является положительно полуопределенным , σ _i будет неотрицательным действительным числом, так что разложение M = UDU ^⁎ также является разложением по сингулярным значениям. В противном случае его можно преобразовать в SVD, переместив фазу e ^iφ каждого σ _i либо в соответствующий ему Vi _, либо в U _i . Естественная связь SVD с ненормальными матрицами осуществляется через теорему полярного разложения : M = SR , где S = UΣU ^⁎ положительно полуопределенный и нормальный, а R = UV ^⁎ унитарный. ${\displaystyle \mathbf {M} =\mathbf {U} \mathbf {D} \mathbf {U} ^{*}}$

Таким образом, за исключением положительных полуопределенных матриц, разложение по собственным значениям и SVD M , хотя и связаны, различаются: разложение по собственным значениям равно M = UDU ⁻¹ , где U не обязательно унитарно, а D не обязательно положительно полуопределенно, а SVD - это M = UΣV ^⁎ , где диагональная и положительно полуопределенная, а U и V - унитарные матрицы, которые не обязательно связаны, кроме как через матрицу M . В то время как только недефектные квадратные матрицы имеют разложение по собственным значениям, любая матрица имеет SVD. ${\displaystyle \mathbf {\Sigma } }$ ${\displaystyle m\times n}$

Применение СВД

Псевдообратный

Разложение по сингулярным значениям можно использовать для вычисления псевдообратной матрицы. Псевдообратная матрица с разложением по сингулярным значениям : ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{\ast }}$

$${\displaystyle \mathbf {M} ^{+}=\mathbf {V} {\boldsymbol {\Sigma }}^{+}\mathbf {U} ^{\ast },}$$

обратнуюлинейных ${\displaystyle {\boldsymbol {\Sigma }}^{+}}$ ${\displaystyle {\boldsymbol {\Sigma }}}$

Решение однородных линейных уравнений

Набор однородных линейных уравнений можно записать как Ax = 0 для матрицы A и вектора x . Типичная ситуация заключается в том, что A известно и необходимо определить ненулевое значение x , удовлетворяющее уравнению. Такой x принадлежит нулевому пространству A и иногда называется (правым) нулевым вектором A . Вектор x можно охарактеризовать как правосингулярный вектор, соответствующий сингулярному значению A , равному нулю. Это наблюдение означает, что если A является квадратной матрицей и не имеет исчезающего сингулярного значения, уравнение не имеет ненулевого x в качестве решения. Это также означает, что если существует несколько исчезающих сингулярных значений, любая линейная комбинация соответствующих правосингулярных векторов является допустимым решением. Аналогично определению (правого) нулевого вектора, ненулевой x, удовлетворяющий x ^⁎ A = 0 , где x ^⁎ обозначает сопряженное транспонирование x , называется левым нулевым вектором A .

Полная минимизация методом наименьших квадратов

Задача полного наименьших квадратов ищет вектор x , который минимизирует 2-норму вектора Ax при ограничении || х || = 1 . Решением оказывается правосингулярный вектор A , соответствующий наименьшему сингулярному значению.

Диапазон, пустое пространство и ранг

Другое применение SVD состоит в том, что он обеспечивает явное представление диапазона и нулевого пространства матрицы M. Правые сингулярные векторы, соответствующие исчезающим сингулярным значениям M , охватывают нулевое пространство M , а левые сингулярные векторы, соответствующие ненулевым сингулярным значениям M , охватывают диапазон M . Например, в приведенном выше примере нулевое пространство охватывает последние две строки V ^⁎ , а диапазон — первые три столбца U .

Как следствие, ранг M равен количеству ненулевых сингулярных значений, которое совпадает с количеством ненулевых диагональных элементов в . В числовой линейной алгебре сингулярные значения могут использоваться для определения эффективного ранга матрицы, поскольку ошибка округления может привести к небольшим, но ненулевым сингулярным значениям в матрице с недостаточным рангом. Предполагается, что сингулярные значения за пределами значительного разрыва численно эквивалентны нулю. ${\displaystyle \mathbf {\Sigma } }$

Приближение матрицы низкого ранга

В некоторых практических приложениях необходимо решить проблему аппроксимации матрицы M другой матрицей , называемой усеченной, которая имеет определенный ранг r . В случае, когда аппроксимация основана на минимизации нормы Фробениуса разности между M и при ограничении , оказывается, что решение дается SVD M , а именно ${\displaystyle {\tilde {\mathbf {M} }}}$ ${\displaystyle {\tilde {\mathbf {M} }}}$ ${\displaystyle \operatorname {rank} \left({\tilde {\mathbf {M} }}\right)=r}$

$${\displaystyle {\tilde {\mathbf {M} }}=\mathbf {U} {\tilde {\boldsymbol {\Sigma }}}\mathbf {V} ^{*},}$$

rтеорема Эккарта-Янга ${\displaystyle {\tilde {\boldsymbol {\Sigma }}}}$ ${\displaystyle \mathbf {\Sigma } }$

Разборные модели

SVD можно рассматривать как разложение матрицы на взвешенную упорядоченную сумму разделимых матриц. Под сепарабельностью мы подразумеваем, что матрица A может быть записана как внешнее произведение двух векторов A = u ⊗ v или, в координатах, . В частности, матрицу M можно разложить как: ${\displaystyle A_{ij}=u_{i}v_{j}}$

$${\displaystyle \mathbf {M} =\sum _{i}\mathbf {A} _{i}=\sum _{i}\sigma _{i}\mathbf {U} _{i}\otimes \mathbf {V} _{i}.}$$

U _iVi _— iσ _iA _iσ _i^{[ нужна цитата ][1]}фильтра Габораобратной корреляцииUV

${\displaystyle \alpha ={\frac {\sigma _{1}^{2}}{\sum _{i}\sigma _{i}^{2}}},}$

которая представляет собой долю мощности в матрице M, которая учитывается первой сепарабельной матрицей в разложении. ^[2]

Ближайшая ортогональная матрица

Можно использовать SVD квадратной матрицы A для определения ортогональной матрицы O , ближайшей к A. Близость соответствия измеряется нормой Фробениуса O − A . Решением является произведение UV ^⁎ . ^[3] Это интуитивно имеет смысл, поскольку ортогональная матрица будет иметь разложение UIV ^⁎ , где I - единичная матрица, так что если A = UΣV ^⁎ , то произведение A = UV ^⁎ представляет собой замену сингулярных значений единицами. Эквивалентно, решением является унитарная матрица R = UV ^⁎ полярного разложения M = RP = P ' R в любом порядке растяжения и вращения, как описано выше.

Похожая проблема, имеющая интересные применения в анализе форм , — это ортогональная задача Прокруста , которая состоит в поиске ортогональной матрицы O , которая наиболее точно отображает A в B. Конкретно,

${\displaystyle \mathbf {O} ={\underset {\Omega }{\operatorname {argmin} }}\|\mathbf {A} {\boldsymbol {\Omega }}-\mathbf {B} \|_{F}\quad {\text{subject to}}\quad {\boldsymbol {\Omega }}^{\operatorname {T} }{\boldsymbol {\Omega }}=\mathbf {I} ,}$

где обозначает норму Фробениуса. ${\displaystyle \|\cdot \|_{F}}$

Эта проблема эквивалентна поиску ближайшей ортогональной матрицы к данной матрице . ${\displaystyle \mathbf {M} =\mathbf {A} ^{\operatorname {T} }\mathbf {B} }$

Алгоритм Кабша

Алгоритм Кабша (в других областях называемый проблемой Вахбы ) использует SVD для вычисления оптимального вращения (относительно минимизации по методу наименьших квадратов), которое выравнивает набор точек с соответствующим набором точек. Он используется, среди прочего, для сравнения структур молекул.

Обработка сигнала

SVD и псевдоинверсия успешно применяются для обработки сигналов , ^[4] обработки изображений ^[5] и больших данных (например, при обработке геномных сигналов). ^{[6] [7] [8] [9]}

Астродинамика

В астродинамике СВД и ее варианты используются как опция для определения подходящих направлений маневра для проектирования траектории перехода ^[10] и удержания орбитальной станции . ^[11]

Другие примеры

SVD также широко применяется для изучения линейных обратных задач и полезен при анализе методов регуляризации, таких как метод Тихонова . Он широко используется в статистике, где он связан с анализом главных компонент и анализом соответствий , а также в обработке сигналов и распознавании образов . Он также используется в модальном анализе только для выходных данных , где немасштабированные формы мод могут быть определены по сингулярным векторам. Еще одно использование — это скрытая семантическая индексация при обработке текста на естественном языке.

В общих численных вычислениях с участием линейных или линеаризованных систем существует универсальная константа, которая характеризует регулярность или сингулярность проблемы, которая является «числом обусловленности» системы . Он часто контролирует частоту ошибок или скорость сходимости данной вычислительной схемы в таких системах. ^{[12] [13]} ${\displaystyle \kappa :=\sigma _{\text{max}}/\sigma _{\text{min}}}$

SVD также играет решающую роль в области квантовой информации в форме, часто называемой разложением Шмидта . Посредством него естественным образом разлагаются состояния двух квантовых систем, обеспечивая необходимое и достаточное условие для их запутанности : если ранг матрицы больше единицы. ${\displaystyle \mathbf {\Sigma } }$

Одним из применений SVD к довольно большим матрицам является численный прогноз погоды , где методы Ланцоша используются для оценки наиболее линейно быстро растущих возмущений в центральном численном прогнозе погоды в течение заданного начального периода вперед; т. е. сингулярные векторы, соответствующие наибольшим сингулярным значениям линеаризованного пропагатора глобальной погоды за этот интервал времени. Выходными сингулярными векторами в этом случае являются целые погодные системы. Эти возмущения затем прогоняются через полную нелинейную модель для создания ансамблевого прогноза , что дает возможность справиться с некоторой неопределенностью, которую следует учитывать в отношении текущего центрального прогноза.

SVD также применяется для моделирования уменьшенного порядка. Целью моделирования пониженного порядка является уменьшение количества степеней свободы в сложной системе, которую необходимо моделировать. SVD сочетался с радиальными базисными функциями для интерполяции решений трехмерных задач нестационарного течения. ^[14]

Интересно, что SVD использовался для улучшения моделирования гравитационных волн с помощью наземного гравитационно-волнового интерферометра aLIGO. ^[15] SVD может помочь повысить точность и скорость генерации сигналов для поддержки поиска гравитационных волн и обновления двух различных моделей сигналов.

Разложение по сингулярным значениям используется в рекомендательных системах для прогнозирования оценок людей. ^[16] С целью расчета СВД на кластерах товарных машин были разработаны распределенные алгоритмы. ^[17]

SVD низкого ранга применялся для обнаружения горячих точек на основе пространственно-временных данных с применением для обнаружения вспышек заболеваний . ^[18] Комбинация SVD и SVD более высокого порядка также применялась для обнаружения событий в реальном времени из сложных потоков данных (многомерные данные с пространственными и временными измерениями) при эпиднадзоре за заболеваниями . ^[19]

Доказательство существования

Собственное значение λ матрицы M характеризуется алгебраическим соотношением Mu = λ u . Когда M является эрмитовым , также доступна вариационная характеристика. Пусть M — вещественная симметричная матрица размера n × n . Определять

$${\displaystyle {\begin{cases}f:\mathbb {R} ^{n}\to \mathbb {R} \\f:\mathbf {x} \mapsto \mathbf {x} ^{\operatorname {T} }\mathbf {M} \mathbf {x} \end{cases}}}$$

теореме о крайних значенияхuхо множителях Лагранжа u

$${\displaystyle \nabla \mathbf {u} ^{\operatorname {T} }\mathbf {M} \mathbf {u} -\lambda \cdot \nabla \mathbf {u} ^{\operatorname {T} }\mathbf {u} =0}$$

λ∇delxM

$${\displaystyle \nabla \mathbf {x} ^{\operatorname {T} }\mathbf {M} \mathbf {x} -\lambda \cdot \nabla \mathbf {x} ^{\operatorname {T} }\mathbf {x} =2(\mathbf {M} -\lambda \mathbf {I} )\mathbf {x} .}$$

Mu = λ uuMv()λM .uf ( x ) = x * M x2 n

Сингулярные значения схожи тем, что их можно описать алгебраически или с помощью вариационных принципов. Хотя, в отличие от случая собственных значений, эрмитичность или симметрия M больше не требуется.

В этом разделе приводятся эти два аргумента в пользу существования разложения по сингулярным значениям.

На основании спектральной теоремы

Пусть — комплексная матрица размера m × n . Поскольку положительно полуопределена и эрмитова, по спектральной теореме существует унитарная матрица размера n × n такая, что ${\displaystyle \mathbf {M} }$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle \mathbf {V} }$

${\displaystyle \mathbf {V} ^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} ={\bar {\mathbf {D} }}={\begin{bmatrix}\mathbf {D} &0\\0&0\end{bmatrix}},}$

где диагональная и положительно определенная, размерности с числом ненулевых собственных значений (что можно показать, чтобы проверить ). Обратите внимание, что здесь по определению матрица, -й столбец которой является -м собственным вектором матрицы , соответствующим собственному значению . Более того, -й столбец , для , является собственным вектором с собственным значением . Это можно выразить, записав как , где столбцы и, следовательно, содержат собственные векторы, соответствующие ненулевым и нулевым собственным значениям соответственно. При таком переписании уравнение принимает вид: ${\displaystyle \mathbf {D} }$ ${\displaystyle \ell \times \ell }$ ${\displaystyle \ell }$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle \ell \leq \min(n,m)}$ ${\displaystyle \mathbf {V} }$ ${\displaystyle i}$ ${\displaystyle i}$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle {\bar {\mathbf {D} }}_{ii}}$ ${\displaystyle j}$ ${\displaystyle \mathbf {V} }$ ${\displaystyle j>\ell }$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle {\bar {\mathbf {D} }}_{jj}=0}$ ${\displaystyle \mathbf {V} }$ ${\displaystyle \mathbf {V} ={\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}}$ ${\displaystyle \mathbf {V} _{1}}$ ${\displaystyle \mathbf {V} _{2}}$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle \mathbf {V} }$

${\displaystyle {\begin{bmatrix}\mathbf {V} _{1}^{*}\\\mathbf {V} _{2}^{*}\end{bmatrix}}\mathbf {M} ^{*}\mathbf {M} {\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}={\begin{bmatrix}\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}&\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}\\\mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}&\mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}\end{bmatrix}}={\begin{bmatrix}\mathbf {D} &0\\0&0\end{bmatrix}}.}$

Это означает, что

${\displaystyle \mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}=\mathbf {D} ,\quad \mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2}=\mathbf {0} .}$

Более того, из второго уравнения следует . ^[20] Наконец, унитарность переводится с точки зрения и в следующие условия: ${\displaystyle \mathbf {M} \mathbf {V} _{2}=\mathbf {0} }$ ${\displaystyle \mathbf {V} }$ ${\displaystyle \mathbf {V} _{1}}$ ${\displaystyle \mathbf {V} _{2}}$

${\displaystyle {\begin{aligned}\mathbf {V} _{1}^{*}\mathbf {V} _{1}&=\mathbf {I} _{1},\\\mathbf {V} _{2}^{*}\mathbf {V} _{2}&=\mathbf {I} _{2},\\\mathbf {V} _{1}\mathbf {V} _{1}^{*}+\mathbf {V} _{2}\mathbf {V} _{2}^{*}&=\mathbf {I} _{12},\end{aligned}}}$

где индексы у единичных матриц используются для обозначения того, что они имеют разные размерности.

Давайте теперь определим

${\displaystyle \mathbf {U} _{1}=\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}.}$

Затем,

${\displaystyle \mathbf {U} _{1}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} (\mathbf {I} -\mathbf {V} _{2}\mathbf {V} _{2}^{*})=\mathbf {M} -(\mathbf {M} \mathbf {V} _{2})\mathbf {V} _{2}^{*}=\mathbf {M} ,}$

т.к. это можно рассматривать и как непосредственное следствие того, что . Это эквивалентно наблюдению, что если — набор собственных векторов, соответствующих ненулевым собственным значениям , то это набор ортогональных векторов и (обычно не полный) набор ортонормированных векторов. Это соответствует использованному выше матричному формализму, обозначающему матрицу, столбцы которой равны , матрице, столбцы которой являются собственными векторами матрицы с исчезающим собственным значением, и матрице, столбцы которой являются векторами . ${\displaystyle \mathbf {M} \mathbf {V} _{2}=\mathbf {0} .}$ ${\displaystyle \mathbf {M} \mathbf {V} _{1}\mathbf {V} _{1}^{*}=\mathbf {M} }$ ${\displaystyle \{{\boldsymbol {v}}_{i}\}_{i=1}^{\ell }}$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle \{\lambda _{i}\}_{i=1}^{\ell }}$ ${\displaystyle \{\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }}$ ${\displaystyle \{\lambda _{i}^{-1/2}\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }}$ ${\displaystyle \mathbf {V} _{1}}$ ${\displaystyle \{{\boldsymbol {v}}_{i}\}_{i=1}^{\ell }}$ ${\displaystyle \mathbf {V} _{2}}$ ${\displaystyle \mathbf {M} ^{*}\mathbf {M} }$ ${\displaystyle \mathbf {U} _{1}}$ ${\displaystyle \{\lambda _{i}^{-1/2}\mathbf {M} {\boldsymbol {v}}_{i}\}_{i=1}^{\ell }}$

Мы видим, что это почти желаемый результат, за исключением того, что и в целом не унитарны, поскольку могут не быть квадратными. Однако мы знаем, что количество строк не меньше количества столбцов, поскольку размерности не больше и . Кроме того, поскольку ${\displaystyle \mathbf {U} _{1}}$ ${\displaystyle \mathbf {V} _{1}}$ ${\displaystyle \mathbf {U} _{1}}$ ${\displaystyle \mathbf {D} }$ ${\displaystyle m}$ ${\displaystyle n}$

${\displaystyle \mathbf {U} _{1}^{*}\mathbf {U} _{1}=\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {V} _{1}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{1}\mathbf {D} ^{-{\frac {1}{2}}}=\mathbf {D} ^{-{\frac {1}{2}}}\mathbf {D} \mathbf {D} ^{-{\frac {1}{2}}}=\mathbf {I_{1}} ,}$

столбцы в них ортонормированы и могут быть расширены до ортонормированного базиса. Это означает, что мы можем выбрать такое, которое унитарно. ${\displaystyle \mathbf {U} _{1}}$ ${\displaystyle \mathbf {U} _{2}}$ ${\displaystyle \mathbf {U} ={\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}}$

Для V ₁ у нас уже есть V ₂ , чтобы сделать его унитарным. Теперь определите

${\displaystyle {\boldsymbol {\Sigma }}={\begin{bmatrix}{\begin{bmatrix}\mathbf {D} ^{\frac {1}{2}}&0\\0&0\end{bmatrix}}\\0\end{bmatrix}},}$

где дополнительные нулевые строки добавляются или удаляются , чтобы количество нулевых строк равнялось количеству столбцов U ₂ , а следовательно, и общим размерам, равным . Затем ${\displaystyle {\boldsymbol {\Sigma }}}$ ${\displaystyle m\times n}$

${\displaystyle {\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}{\begin{bmatrix}{\begin{bmatrix}\mathbf {} D^{\frac {1}{2}}&0\\0&0\end{bmatrix}}\\0\end{bmatrix}}{\begin{bmatrix}\mathbf {V} _{1}&\mathbf {V} _{2}\end{bmatrix}}^{*}={\begin{bmatrix}\mathbf {U} _{1}&\mathbf {U} _{2}\end{bmatrix}}{\begin{bmatrix}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}\\0\end{bmatrix}}=\mathbf {U} _{1}\mathbf {D} ^{\frac {1}{2}}\mathbf {V} _{1}^{*}=\mathbf {M} ,}$

какой желаемый результат:

${\displaystyle \mathbf {M} =\mathbf {U} {\boldsymbol {\Sigma }}\mathbf {V} ^{*}.}$

Обратите внимание, что аргумент может начаться с диагонализации MM ^⁎, а не M ^⁎ M (это непосредственно показывает, что MM ^⁎ и M ^⁎ M имеют одинаковые ненулевые собственные значения).

На основе вариационной характеристики

Сингулярные значения также можно охарактеризовать как максимумы u ^T Mv , рассматриваемые как функция u и v , в определенных подпространствах. Сингулярные векторы — это значения u и v , при которых достигаются эти максимумы.

Пусть M обозначает матрицу размера m × n с вещественными элементами. Пусть S ^{k −1} – единичная -сфера в , и определим ${\displaystyle (k-1)}$ ${\displaystyle \mathbb {R} ^{k}}$ ${\displaystyle \sigma (\mathbf {u} ,\mathbf {v} )=\mathbf {u} ^{\operatorname {T} }\mathbf {M} \mathbf {v} ,\ \mathbf {u} \in S^{m-1},\mathbf {v} \in S^{n-1}.}$

Рассмотрим функцию σ , ограниченную S ^{m −1} × S ^{n −1} . Поскольку и S ^{m −1} , и Sn ⁻¹ являются компактными множествами, их ^{произведение} также компактно. Более того, поскольку σ непрерывна, она достигает максимального значения хотя бы для одной пары векторов u ∈ Sm ^{− 1} и v ∈ Sn ^{− 1} . Это наибольшее значение обозначается σ ₁ , а соответствующие векторы обозначаются u ₁ и v ₁ . Поскольку σ ₁ является наибольшим значением σ ( u , v ), оно должно быть неотрицательным. Если бы оно было отрицательным, изменение знака u ₁ или v ₁ сделало бы его положительным и, следовательно, больше.

Заявление. u ₁ , v ₁ — левые и право-сингулярные векторы M с соответствующим сингулярным значением σ ₁ .

Доказательство. Как и в случае с собственными значениями, по предположению, два вектора удовлетворяют уравнению множителя Лагранжа:

${\displaystyle \nabla \sigma =\nabla \mathbf {u} ^{\operatorname {T} }\mathbf {M} \mathbf {v} -\lambda _{1}\cdot \nabla \mathbf {u} ^{\operatorname {T} }\mathbf {u} -\lambda _{2}\cdot \nabla \mathbf {v} ^{\operatorname {T} }\mathbf {v} }$

После некоторой алгебры это становится

${\displaystyle {\begin{aligned}\mathbf {M} \mathbf {v} _{1}&=2\lambda _{1}\mathbf {u} _{1}+0\\\mathbf {M} ^{\operatorname {T} }\mathbf {u} _{1}&=0+2\lambda _{2}\mathbf {v} _{1}\end{aligned}}}$

Умножив первое уравнение слева на и второе уравнение слева на и взяв || ты || = || в || = 1 учет дает ${\displaystyle \mathbf {u} _{1}^{\operatorname {T} }}$ ${\displaystyle \mathbf {v} _{1}^{\operatorname {T} }}$

${\displaystyle \sigma _{1}=2\lambda _{1}=2\lambda _{2}.}$

Подставив это в пару приведенных выше уравнений, мы имеем

${\displaystyle {\begin{aligned}\mathbf {M} \mathbf {v} _{1}&=\sigma _{1}\mathbf {u} _{1}\\\mathbf {M} ^{\operatorname {T} }\mathbf {u} _{1}&=\sigma _{1}\mathbf {v} _{1}\end{aligned}}}$

Это доказывает утверждение.

Больше сингулярных векторов и сингулярных значений можно найти путем максимизации σ ( u , v ) по нормализованным u , v , которые ортогональны u ₁ и v ₁ соответственно.

Переход от вещественного к комплексному аналогичен случаю собственных значений.

Расчет СВД

Разложение по сингулярным значениям можно вычислить, используя следующие наблюдения:

• Левосингулярные векторы M представляют собой набор ортонормированных собственных векторов MM ^⁎ .
• Правосингулярные векторы M представляют собой набор ортонормированных собственных векторов M ^⁎ M .
• Ненулевые сингулярные значения M (найденные на диагональных элементах ) являются квадратными корнями ненулевых собственных значений как M ^⁎ M , так и MM ^⁎ . ${\displaystyle \mathbf {\Sigma } }$

Численный подход

SVD матрицы M обычно вычисляется с помощью двухэтапной процедуры. На первом этапе матрица сводится к двудиагональной матрице . Для этого требуется O ( mn ² ) операций с плавающей запятой (флоп), предполагая, что m ≥ n . Второй шаг — вычислить SVD двудиагональной матрицы. Этот шаг можно выполнить только итеративным методом (как в случае с алгоритмами собственных значений ). Однако на практике достаточно вычислить СВД с определенной точностью, как машинный эпсилон . Если эту точность считать постоянной, то второй шаг занимает O( n ) итераций, каждая из которых стоит O( n ) флопов. Таким образом, первый шаг обходится дороже, а общая стоимость составляет O( mn ² ) флопов (Trefethen & Bau III 1997, лекция 31).

Первый шаг можно сделать с помощью отражений Хаусхолдера за 4 миллиона ²  - 4 n ^3/3 флопа, предполагая, что нужны только сингулярные значения, а не сингулярные векторы. Если m намного больше n , то выгодно сначала привести матрицу M к треугольной матрице с помощью QR-разложения , а затем использовать отражения Хаусхолдера для дальнейшего приведения матрицы к двудиагональной форме; общая стоимость равна 2 млн ²  + 2 n ³ флопа (Trethethen & Bau III, 1997, лекция 31).

Второй шаг можно выполнить с помощью варианта QR-алгоритма для вычисления собственных значений, который впервые был описан Голубом и Каханом (1965). Подпрограмма LAPACK DBDSQR ^[21] реализует этот итерационный метод с некоторыми модификациями, позволяющими охватить случай, когда сингулярные значения очень малы (Demmel & Kahan 1990). Вместе с первым шагом, использующим отражения Хаусхолдера и, при необходимости, QR-разложение, это образует процедуру DGESVD ^[22] для вычисления сингулярного разложения.

Тот же алгоритм реализован в Научной библиотеке GNU (GSL). GSL также предлагает альтернативный метод, который использует одностороннюю ортогонализацию Якоби на этапе 2 (GSL Team 2007). Этот метод вычисляет SVD двудиагональной матрицы путем решения последовательности задач SVD 2 × 2, аналогично тому, как алгоритм собственных значений Якоби решает последовательность методов собственных значений 2 × 2 (Golub & Van Loan 1996, §8.6.3). Еще один метод для шага 2 использует идею алгоритма собственных значений «разделяй и властвуй» (Trefethen & Bau III 1997, лекция 31).

Существует альтернативный способ, который явно не использует разложение по собственным значениям. ^[23] Обычно сингулярную задачу матрицы M преобразуют в эквивалентную симметричную задачу собственных значений, такую ​​как MM ^⁎ , M ^⁎ M или

${\displaystyle {\begin{bmatrix}\mathbf {0} &\mathbf {M} \\\mathbf {M} ^{*}&\mathbf {0} \end{bmatrix}}.}$

Подходы, использующие разложение по собственным значениям, основаны на алгоритме QR , который хорошо разработан, чтобы быть стабильным и быстрым. Обратите внимание, что сингулярные значения являются действительными, а право- и левосингулярные векторы не требуются для формирования преобразований подобия. Можно итеративно чередовать QR-разложение и LQ-разложение , чтобы найти действительные диагональные эрмитовы матрицы . QR -разложение дает M ⇒ QR , а LQ - разложение R дает R ⇒ LP ^⁎ . Таким образом, на каждой итерации мы имеем M ⇒ QLP ^⁎ , обновляем M ⇐ L и повторяем ортогонализации. В конце концов, ^{[ необходимы пояснения ]} эта итерация между QR-разложением и LQ-разложением дает левые и правые унитарные сингулярные матрицы. Этот подход нельзя легко ускорить, как это можно сделать с помощью алгоритма QR с помощью спектральных сдвигов или дефляции. Это связано с тем, что метод сдвига нелегко определить без использования преобразований подобия. Однако этот итеративный подход очень прост в реализации, поэтому он является хорошим выбором, когда скорость не имеет значения. Этот метод также дает представление о том, как чисто ортогональные/унитарные преобразования могут получить SVD.

Аналитический результат 2×2 СВД

Сингулярные значения матрицы 2 × 2 можно найти аналитически. Пусть матрица будет ${\displaystyle \mathbf {M} =z_{0}\mathbf {I} +z_{1}\sigma _{1}+z_{2}\sigma _{2}+z_{3}\sigma _{3}}$

где – комплексные числа, параметризующие матрицу, I – единичная матрица и обозначают матрицы Паули . Тогда два его сингулярных значения определяются выражением ${\displaystyle z_{i}\in \mathbb {C} }$ ${\displaystyle \sigma _{i}}$

${\displaystyle {\begin{aligned}\sigma _{\pm }&={\sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm {\sqrt {(|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2})^{2}-|z_{0}^{2}-z_{1}^{2}-z_{2}^{2}-z_{3}^{2}|^{2}}}}}\\&={\sqrt {|z_{0}|^{2}+|z_{1}|^{2}+|z_{2}|^{2}+|z_{3}|^{2}\pm 2{\sqrt {(\operatorname {Re} z_{0}z_{1}^{*})^{2}+(\operatorname {Re} z_{0}z_{2}^{*})^{2}+(\operatorname {Re} z_{0}z_{3}^{*})^{2}+(\operatorname {Im} z_{1}z_{2}^{*})^{2}+(\operatorname {Im} z_{2}z_{3}^{*})^{2}+(\operatorname {Im} z_{3}z_{1}^{*})^{2}}}}}\end{aligned}}}$

Уменьшенные СВД

Визуализация уменьшенных вариантов СВД. Сверху вниз: 1: Полный SVD, 2: Тонкий SVD (удалить столбцы U, не соответствующие строкам V*), 3: Компактный SVD (удалить исчезающие сингулярные значения и соответствующие столбцы/строки в U и V*), 4 : Усеченный SVD (сохраняется только t наибольших сингулярных значений и соответствующие столбцы/строки в U и V*)

В приложениях довольно редко требуется полное SVD, включая полное унитарное разложение нулевого пространства матрицы. Вместо этого часто бывает достаточно (а также быстрее и экономичнее с точки зрения хранения) вычислить уменьшенную версию SVD. Для матрицы M размера m × n ранга r можно выделить следующее :

Тонкая СВД

Тонкий или экономичный SVD матрицы M определяется выражением ^[24]

${\displaystyle \mathbf {M} =\mathbf {U} _{k}{\boldsymbol {\Sigma }}_{k}\mathbf {V} _{k}^{*},}$

где

${\displaystyle k=\operatorname {min} (m,n)}$,

матрицы U _k и V _k содержат только первые k столбцов U и V , а Σ _k содержит только первые k сингулярных значений из Σ. Таким образом, матрица U _k имеет размер m × k , Σ _k — диагональ k × k , а V _k * — k × n .

Тонкий SVD использует значительно меньше места и времени вычислений, если k  ≪ max( m , n ). Первым этапом расчета обычно будет QR-разложение M , что в этом случае может значительно ускорить расчет.

Компактная СВД

${\displaystyle \mathbf {M} =\mathbf {U} _{r}{\boldsymbol {\Sigma }}_{r}\mathbf {V} _{r}^{*}}$

Вычисляются только r векторов-столбцов U и r векторов-строк V* , соответствующих ненулевым сингулярным значениям Σ _r . Остальные векторы U и V* не рассчитываются. Это быстрее и экономичнее, чем тонкий СВД, если r  ≪ min( m , n ). Таким образом, матрица U _r имеет размер m × r , Σ _r — диагональ r × r , а V _r * — это r × n .

Усеченная СВД

Во многих приложениях число r ненулевых сингулярных значений велико, что делает невозможным вычисление даже Compact SVD. В таких случаях наименьшие сингулярные значения, возможно, придется усечь, чтобы вычислить только t  ≪  r ненулевых сингулярных значений. Усеченный SVD больше не является точным разложением исходной матрицы M , а скорее обеспечивает оптимальную аппроксимацию матрицы низкого ранга любой матрицей фиксированного ранга  t. ${\displaystyle {\tilde {\mathbf {M} }}}$

${\displaystyle {\tilde {\mathbf {M} }}=\mathbf {U} _{t}{\boldsymbol {\Sigma }}_{t}\mathbf {V} _{t}^{*}}$,

где матрица U _t равна m × t , Σ _t — диагональ t × t , а V _t * — t × n . Вычисляются только t векторов-столбцов U и t векторов-строк V* , соответствующих t наибольшим сингулярным значениям Σ _t . Это может быть намного быстрее и экономичнее, чем компактный SVD, если t ≪ r , но требует совершенно другого набора инструментов числовых решателей.

В приложениях, требующих приближения к обратной матрице Мура-Пенроуза M , интерес представляют наименьшие сингулярные значения M , вычислить которые сложнее, чем самые большие.

Усеченный SVD используется при скрытой семантической индексации . ^[25]

Нормы

Нормы Кай Фана

Сумма k крупнейших сингулярных значений M является матричной нормой , k -нормой Ky Fan M. ^[26]

Первая из норм Кай Фана, 1-норма Кай Фана, совпадает с операторной нормой M как линейного оператора относительно евклидовых норм K ^m и K ⁿ . Другими словами, 1-норма Кай Фана — это норма оператора, индуцированная стандартным ℓ ² евклидовым скалярным произведением. По этой причине его еще называют оператором 2-нормы. Легко проверить связь между 1-нормой Кай Фана и сингулярными значениями. В общем случае это верно для ограниченного оператора M в (возможно, бесконечномерном) гильбертовом пространстве.

${\displaystyle \|\mathbf {M} \|=\|\mathbf {M} ^{*}\mathbf {M} \|^{\frac {1}{2}}}$

Но в матричном случае ( M* M ) ^1/2 является нормальной матрицей , поэтому || М* М || ^1/2 является наибольшим собственным значением ( M* M ) ^1/2 , т.е. наибольшим сингулярным значением M .

Последняя из норм Кай Фана, сумма всех сингулярных значений, является нормой следа (также известной как «ядерная норма»), определяемой || М || = Tr[( M* M ) ^1/2 ] (собственные значения M* M представляют собой квадраты сингулярных значений).

Норма Гильберта – Шмидта

Сингулярные значения связаны с другой нормой в пространстве операторов. Рассмотрим скалярное произведение Гильберта–Шмидта на матрицах размера n × n , определяемое формулой

${\displaystyle \langle \mathbf {M} ,\mathbf {N} \rangle =\operatorname {tr} \left(\mathbf {N} ^{*}\mathbf {M} \right).}$

Таким образом, индуцированная норма равна

${\displaystyle \|\mathbf {M} \|={\sqrt {\langle \mathbf {M} ,\mathbf {M} \rangle }}={\sqrt {\operatorname {tr} \left(\mathbf {M} ^{*}\mathbf {M} \right)}}.}$

Поскольку след инвариантен относительно унитарной эквивалентности, это показывает

${\displaystyle \|\mathbf {M} \|={\sqrt {\sum _{i}\sigma _{i}^{2}}}}$

где σi _— сингулярные значения M. Это называется нормой Фробениуса , 2-нормой Шаттена или нормой Гильберта– Шмидта M. Непосредственный расчет показывает, что норма Фробениуса M = ( m _ij ) совпадает с:

${\displaystyle {\sqrt {\sum _{ij}|m_{ij}|^{2}}}.}$

Кроме того, норма Фробениуса и норма следа (ядерная норма) являются частными случаями нормы Шаттена .

Вариации и обобщения

Масштабно-инвариантный СВД

Сингулярные значения матрицы A однозначно определены и инвариантны относительно левых и/или правых унитарных преобразований A . Другими словами, сингулярные значения UAV для унитарных U и V равны сингулярным значениям A. Это важное свойство для приложений, в которых необходимо сохранить евклидовы расстояния и инвариантность относительно вращений.

Масштабно-инвариантный SVD, или SI-SVD, ^[27] аналогичен обычному SVD, за исключением того, что его однозначно определенные сингулярные значения инвариантны относительно диагональных преобразований A . Другими словами, сингулярные значения DAE для обратимых диагональных матриц D и E равны сингулярным значениям A. Это важное свойство для приложений, для которых необходима инвариантность к выбору единиц измерения переменных (например, метрических или имперских единиц).

Ограниченные операторы в гильбертовых пространствах

Факторизация M = UΣV ^⁎ может быть расширена до ограниченного оператора M в сепарабельном гильбертовом пространстве H . А именно, для любого ограниченного оператора M существуют частичная изометрия U , унитарное V , пространство с мерой ( X ,  µ ) и неотрицательное измеримое f такие, что

${\displaystyle \mathbf {M} =\mathbf {U} T_{f}\mathbf {V} ^{*}}$

где – умножение на f на L ² ( X , µ ). ${\displaystyle T_{f}}$

Это можно показать, подражая линейному алгебраическому аргументу для матричного случая, приведенного выше. VT _f V * — это уникальный положительный квадратный корень из M*M , заданный борелевским функциональным исчислением для самосопряженных операторов . Причина, по которой U не обязательно должна быть унитарной, заключается в том, что, в отличие от конечномерного случая, при заданной изометрии U ₁ с нетривиальным ядром не может быть найдено подходящее U ₂ такое, что

${\displaystyle {\begin{bmatrix}U_{1}\\U_{2}\end{bmatrix}}}$

является унитарным оператором.

Что касается матриц, то факторизация сингулярных значений эквивалентна полярному разложению операторов: мы можем просто написать

${\displaystyle \mathbf {M} =\mathbf {U} \mathbf {V} ^{*}\cdot \mathbf {V} T_{f}\mathbf {V} ^{*}}$

и обратите внимание, что UV* по-прежнему является частичной изометрией, тогда как VT _f V * положителен.

Сингулярные значения и компактные операторы

Понятие сингулярных значений и лево/правосингулярных векторов можно расширить до компактного оператора в гильбертовом пространстве, поскольку они имеют дискретный спектр. Если T компактно, каждое ненулевое λ в его спектре является собственным значением. Более того, компактный самосопряженный оператор можно диагонализовать по собственным векторам. Если M компактно, компактно и M ^⁎ M . Применяя результат диагонализации, унитарный образ своего положительного квадратного корня T _f  имеет набор ортонормированных собственных векторов { e _i } , соответствующих строго положительным собственным значениям { σ _i } . Для любого ψ ∈ H

${\displaystyle \mathbf {M} \psi =\mathbf {U} T_{f}\mathbf {V} ^{*}\psi =\sum _{i}\left\langle \mathbf {U} T_{f}\mathbf {V} ^{*}\psi ,\mathbf {U} e_{i}\right\rangle \mathbf {U} e_{i}=\sum _{i}\sigma _{i}\left\langle \psi ,\mathbf {V} e_{i}\right\rangle \mathbf {U} e_{i},}$

где ряд сходится в топологии нормы на H . Обратите внимание, как это похоже на выражение из конечномерного случая. σ _i называются сингулярными значениями M . { U e _i } (соответственно { V e _i } ) можно считать лево-сингулярными (соответственно право-сингулярными) векторами M .

Компактные операторы в гильбертовом пространстве являются замыканием операторов конечного ранга в равномерной операторной топологии. Приведенное выше выражение ряда дает явное такое представление. Непосредственным следствием этого является:

Теорема. M компактен тогда и только тогда, когда M ^⁎ M компактен.

История

Разложение по сингулярным значениям первоначально было разработано дифференциальными геометрами , которые хотели определить, можно ли сделать действительную билинейную форму равной другой путем независимых ортогональных преобразований двух пространств, на которые она действует. Эухенио Бельтрами и Камилла Джордан независимо открыли в 1873 и 1874 годах соответственно, что сингулярные значения билинейных форм, представленные в виде матрицы, образуют полный набор инвариантов для билинейных форм при ортогональных заменах. Джеймс Джозеф Сильвестр также пришел к разложению по сингулярным значениям для действительных квадратных матриц в 1889 году, по-видимому, независимо от Бельтрами и Джордана. Сильвестр назвал сингулярные значения каноническими множителями матрицы A. Четвертым математиком, независимо открывшим разложение по сингулярным числам, является Отонн в 1915 году, который пришел к нему с помощью полярного разложения . Первое доказательство разложения по сингулярным значениям для прямоугольных и комплексных матриц было сделано Карлом Эккартом и Гейлом Дж. Янгом в 1936 году; ^{В [28]} они рассматривали это как обобщение преобразования главной оси для эрмитовых матриц .

В 1907 году Эрхард Шмидт определил аналог сингулярных значений для интегральных операторов (которые компактны при некоторых слабых технических предположениях); похоже, он не знал о параллельных работах по сингулярным значениям конечных матриц. Эта теория была далее развита Эмилем Пикаром в 1910 году, который первым назвал числа сингулярными значениями (или по-французски valeurs Singleières ). ${\displaystyle \sigma _{k}}$

Практические методы вычисления SVD восходят к Когбетлянцу в 1954–1955 годах и Хестенесу в 1958 году ^[29] и очень напоминают алгоритм собственных значений Якоби , который использует вращения плоскости или вращения Гивенса . Однако они были заменены методом Джина Голуба и Уильяма Кахана , опубликованным в 1965 году ^[30] , который использует преобразования или отражения Хаусхолдера . В 1970 году Голуб и Кристиан Рейнш ^[31] опубликовали вариант алгоритма Голуба/Кахана, который до сих пор является наиболее используемым.

Смотрите также

• Каноническая корреляция
• Каноническая форма
• Анализ соответствия (СА)
• Проклятие размерности
• Цифровая обработка сигналов
• Уменьшение размерности
• Собственное разложение матрицы
• Эмпирические ортогональные функции (ЭОФ)
• Фурье-анализ
• Обобщенное разложение по сингулярным значениям
• Неравенства относительно сингулярных значений
• К-СВД
• Скрытый семантический анализ
• Скрытая семантическая индексация
• Линейный метод наименьших квадратов
• Список преобразований, связанных с Фурье
• Хэширование с учетом местоположения
• Низкоранговое приближение
• Разложение матрицы
• Многолинейный анализ главных компонент (MPCA)
• Поиск ближайшего соседа
• Нелинейный итеративный частичный метод наименьших квадратов
• Полярное разложение
• Анализ главных компонентов (PCA)
• Разложение Шмидта
• Смит, нормальная форма
• Единственное значение
• Временная последовательность
• Двумерное сингулярное разложение (2DSVD)
• неравенство следов фон Неймана
• Вейвлет-сжатие

Примечания

1. ДеАнджелис, GC; Одзава, И.; Фриман, Р.Д. (октябрь 1995 г.). «Динамика рецептивных полей в центральных зрительных путях». Тенденции нейробиологии . 18 (10): 451–8. дои : 10.1016/0166-2236(95)94496-Р. PMID  8545912. S2CID  12827601.
2. Депирё, Д.А.; Саймон, Джей Зи; Кляйн, диджей; Шамма, SA (март 2001 г.). «Характеристика спектрально-временного поля реакции с динамическими пульсациями в первичной слуховой коре хорька». Дж. Нейрофизиология . 85 (3): 1220–34. дои : 10.1152/jn.2001.85.3.1220. ПМИД  11247991.
3. Разложение по сингулярным значениям при симметричной (Lowdin) ортогонализации и сжатии данных
4. Сахидулла, Мэриленд; Киннунен, Томи (март 2016 г.). «Функции локальной спектральной изменчивости для проверки динамиков». Цифровая обработка сигналов . 50 : 1–11. дои : 10.1016/j.dsp.2015.10.011.
5. Мадемлис, Иоаннис; Тефас, Анастасиос; Питас, Иоаннис (2018). «Регуляризованная значимость видеокадров на основе SVD для обобщения видео неконтролируемых действий». Международная конференция IEEE по акустике, речи и обработке сигналов (ICASSP) 2018 г. IEEE. стр. 2691–2695. дои : 10.1109/ICASSP.2018.8462274. ISBN 978-1-5386-4658-8. S2CID  52286352 . Проверено 19 января 2023 г.
6. О. Альтер, П.О. Браун и Д. Ботштейн (сентябрь 2000 г.). «Разложение по сингулярным значениям для обработки и моделирования данных общегеномной экспрессии». ПНАС . 97 (18): 10101–10106. Бибкод : 2000PNAS...9710101A. дои : 10.1073/pnas.97.18.10101 . ПМК 27718 . ПМИД  10963673. 
7. О. Альтер; Голубь Г.Х. (ноябрь 2004 г.). «Интегративный анализ данных в масштабе генома с использованием псевдообратной проекции предсказывает новую корреляцию между репликацией ДНК и транскрипцией РНК». ПНАС . 101 (47): 16577–16582. Бибкод : 2004PNAS..10116577A. дои : 10.1073/pnas.0406767101 . ПМК 534520 . ПМИД  15545604. 
8. О. Альтер; Голубь Г.Х. (август 2006 г.). «Разложение по сингулярным значениям распределения длин мРНК в масштабе генома выявляет асимметрию в расширении полосы гель-электрофореза РНК». ПНАС . 103 (32): 11828–11833. Бибкод : 2006PNAS..10311828A. дои : 10.1073/pnas.0604756103 . ПМЦ 1524674 . ПМИД  16877539. 
9. Бертаньолли, Нью-Мексико; Дрейк, Дж.А.; Теннессен, Дж. М.; Альтер, О. (ноябрь 2013 г.). «SVD идентифицирует функции распределения длины транскрипта на основе данных микрочипов ДНК и выявляет эволюционные силы, глобально влияющие на метаболизм GBM». ПЛОС ОДИН . 8 (11): е78913. Бибкод : 2013PLoSO...878913B. дои : 10.1371/journal.pone.0078913 . ПМЦ 3839928 . PMID  24282503. Выделите. 
10. Муралидхаран, Вивек; Хауэлл, Кэтлин (2023). «Направления растяжения в окололунном пространстве: Заявки на вылеты и проектирование трансферов». Астродинамика . 7 (2): 153–178. Бибкод : 2023AsDyn...7..153M. doi : 10.1007/s42064-022-0147-z. S2CID  252637213.
11. Муралидхаран, Вивек; Хауэлл, Кэтлин (2022). «Использование направлений растяжения для поддержания положения на галоорбитах Земля-Луна». Достижения в космических исследованиях . 69 (1): 620–646. Бибкод : 2022AdSpR..69..620M. дои : 10.1016/j.asr.2021.10.028. S2CID  239490016.
12. Эдельман, Алан (1992). «О распределении масштабированного числа состояния» (PDF) . Математика. Комп . 58 (197): 185–190. Бибкод : 1992MaCom..58..185E. дои : 10.1090/S0025-5718-1992-1106966-2 .
13. Шен, Цзяньхун (Джеки) (2001). «Об сингулярных значениях гауссовских случайных матриц». Линейный Алг. Приложение . 326 (1–3): 1–14. дои : 10.1016/S0024-3795(00)00322-0 .
14. Уолтон, С.; Хасан, О.; Морган, К. (2013). «Моделирование пониженного порядка нестационарного потока жидкости с использованием правильного ортогонального разложения и радиальных базисных функций». Прикладное математическое моделирование . 37 (20–21): 8930–8945. дои : 10.1016/j.apm.2013.04.025 .
15. Сетьявати, Ю.; Оме, Ф.; Хан, С. (2019). «Улучшение модели гравитационных сигналов посредством динамической калибровки». Физический обзор D . 99 (2): 024010. arXiv : 1810.07060 . Бибкод : 2019PhRvD..99b4010S. doi : 10.1103/PhysRevD.99.024010. S2CID  118935941.
16. Сарвар, Бадрул; Карипис, Георгий; Констан, Джозеф А. и Ридл, Джон Т. (2000). «Применение уменьшения размерности в рекомендательной системе – практический пример» (PDF) . Университет Миннесоты . {{cite journal}}: Требуется цитировать журнал |journal=( помощь )
17. Босаг Заде, Реза; Карлссон, Гуннар (2013). «Квадрат матрицы, не зависящий от измерения, с использованием MapReduce» (PDF) . arXiv : 1304.1467 . Бибкод : 2013arXiv1304.1467B. {{cite journal}}: Требуется цитировать журнал |journal=( помощь )
18. Хади Фанаи Торк; Жоау Гама (сентябрь 2014 г.). «Метод собственного пространства для обнаружения пространственно-временных горячих точек». Экспертные системы . 32 (3): 454–464. arXiv : 1406.3506 . Бибкод : 2014arXiv1406.3506F. дои : 10.1111/exsy.12088. S2CID  15476557.
19. Хади Фанаи Торк; Жоау Гама (май 2015 г.). «EigenEvent: алгоритм обнаружения событий из сложных потоков данных при синдромном наблюдении». Интеллектуальный анализ данных . 19 (3): 597–616. arXiv : 1406.3496 . дои : 10.3233/IDA-150734. S2CID  17966555.
20. Чтобы увидеть это, нам просто нужно заметить это и запомнить это . ${\displaystyle \operatorname {Tr} (\mathbf {V} _{2}^{*}\mathbf {M} ^{*}\mathbf {M} \mathbf {V} _{2})=\|\mathbf {M} \mathbf {V} _{2}\|^{2}}$ ${\displaystyle \|A\|=0\Leftrightarrow A=0}$
21. Netlib.org
22. Netlib.org
23. mathworks.co.kr/matlabcentral/fileexchange/12674-simple-svd
24. Деммель, Джеймс (2000). «Разложения». Шаблоны для решения алгебраических задач на собственные значения. Бай, Чжаоцзюнь; Деммель, Джеймс; Донгарра, Джек Дж.; Руэ, Аксель; ван дер Ворст, Хенк А. Общество промышленной и прикладной математики. дои : 10.1137/1.9780898719581. ISBN 978-0-89871-471-5.
25. Чикко, Д; Массероли, М (2015). «Программный пакет для прогнозирования аннотаций генов и белков и поиска сходства». Транзакции IEEE/ACM по вычислительной биологии и биоинформатике . 12 (4): 837–843. дои : 10.1109/TCBB.2014.2382127. hdl : 11311/959408 . PMID  26357324. S2CID  14714823.
26. Фан, Кентукки (1951). «Максимальные свойства и неравенства для собственных значений вполне непрерывных операторов». Труды Национальной академии наук Соединенных Штатов Америки . 37 (11): 760–766. Бибкод : 1951PNAS...37..760F. дои : 10.1073/pnas.37.11.760 . ПМЦ 1063464 . ПМИД  16578416. 
27. Ульманн, Джеффри (2018), Обобщенная обратная матрица, согласующаяся с диагональными преобразованиями (PDF) , SIAM Journal on Matrix Analysis, vol. 239, стр. 781–800, заархивировано из оригинала (PDF) 7 марта 2019 г.
28. Эккарт, К .; Янг, Г. (1936). «Приближение одной матрицы другой меньшего ранга». Психометрика . 1 (3): 211–8. дои : 10.1007/BF02288367. S2CID  10163399.
29. Хестенес, MR (1958). «Обращение матриц путем биортогонализации и связанные с этим результаты». Журнал Общества промышленной и прикладной математики . 6 (1): 51–90. дои : 10.1137/0106005. JSTOR  2098862. MR  0092215.
30. (Голуб и Кахан, 1965)
31. Голуб, Г.Х .; Рейнш, К. (1970). «Разложение по сингулярным значениям и решения методом наименьших квадратов». Нумерическая математика . 14 (5): 403–420. дои : 10.1007/BF02163027. MR  1553974. S2CID  123532178.

Рекомендации

• Банерджи, Судипто; Рой, Аниндья (2014), Линейная алгебра и матричный анализ для статистики , Тексты по статистическим наукам (1-е изд.), Чепмен и Холл / CRC, ISBN 978-1420095388
• Бисгард, Джеймс (2021). Анализ и линейная алгебра: разложение по сингулярным значениям и приложения . Студенческая математическая библиотека (1-е изд.). АМС. ISBN 978-1-4704-6332-8.
• Чикко, Д; Массероли, М (2015). «Программный пакет для прогнозирования аннотаций генов и белков и поиска сходства». Транзакции IEEE/ACM по вычислительной биологии и биоинформатике . 12 (4): 837–843. дои : 10.1109/TCBB.2014.2382127. hdl : 11311/959408 . PMID  26357324. S2CID  14714823.
• Трефетен, Ллойд Н .; Бау III, Дэвид (1997). Численная линейная алгебра . Филадельфия: Общество промышленной и прикладной математики. ISBN 978-0-89871-361-9.
• Деммель, Джеймс ; Кахан, Уильям (1990). «Точные сингулярные значения двудиагональных матриц». Журнал SIAM по научным и статистическим вычислениям . 11 (5): 873–912. CiteSeerX  10.1.1.48.3740 . дои : 10.1137/0911052.
• Голуб, Джин Х .; Кахан, Уильям (1965). «Вычисление сингулярных значений и псевдообратной матрицы». Журнал Общества промышленной и прикладной математики, серия B: Численный анализ . 2 (2): 205–224. Бибкод : 1965SJNA....2..205G. дои : 10.1137/0702016. JSTOR  2949777.
• Голуб, Джин Х .; Ван Лоан, Чарльз Ф. (1996). Матричные вычисления (3-е изд.). Джонс Хопкинс. ISBN 978-0-8018-5414-9.
• Команда GSL (2007). «§14.4 Разложение по сингулярным значениям». Научная библиотека ГНУ. Справочное руководство .
• Халлдор, Бьернссон и Венегас, Сильвия А. (1997). «Руководство по анализу климатических данных EOF и SVD». Университет Макгилла, Отчет CCGCR № 97-1, Монреаль, Квебек, 52 стр.
• Хансен, ПК (1987). «Усеченный СВД как метод регуляризации». КУСОЧЕК . 27 (4): 534–553. дои : 10.1007/BF01937276. S2CID  37591557.
• Хорн, Роджер А.; Джонсон, Чарльз Р. (1985). «Раздел 7.3». Матричный анализ . Издательство Кембриджского университета. ISBN 978-0-521-38632-6.
• Хорн, Роджер А.; Джонсон, Чарльз Р. (1991). "Глава 3" . Темы матричного анализа . Издательство Кембриджского университета. ISBN 978-0-521-46713-1.
• Самет, Х. (2006). Основы многомерных и метрических структур данных . Морган Кауфманн. ISBN 978-0-12-369446-1.
• Стрэнг Г. (1998). «Раздел 6.7». Введение в линейную алгебру (3-е изд.). Уэлсли-Кембридж Пресс. ISBN 978-0-9614088-5-5.
• Стюарт, GW (1993). «О ранней истории разложения сингулярных значений». Обзор СИАМ . 35 (4): 551–566. CiteSeerX  10.1.1.23.1831 . дои : 10.1137/1035134. hdl : 1903/566. JSTOR  2132388.
• Уолл, Майкл Э.; Рехтштайнер, Андреас; Роша, Луис М. (2003). «Разложение по сингулярным значениям и анализ главных компонент». В ДП Беррар; В. Дубицкий; М. Гранцов (ред.). Практический подход к анализу данных микрочипов . Норвелл, Массачусетс: Клювер. стр. 91–109.
• Пресс, WH; Теукольский, С.А.; Феттерлинг, WT; Фланнери, BP (2007), «Раздел 2.6», Численные рецепты: искусство научных вычислений (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8

Внешние ссылки

• Онлайн калькулятор СВД