Акустический резонанс — это явление, при котором акустическая система усиливает звуковые волны, частота которых совпадает с одной из ее собственных частот колебаний (ее резонансными частотами ).
Термин «акустический резонанс» иногда используется для сужения механического резонанса до диапазона частот человеческого слуха, но поскольку акустика определяется в общих чертах относительно колебательных волн в веществе, [1] акустический резонанс может возникать на частотах за пределами диапазона человеческого слуха.
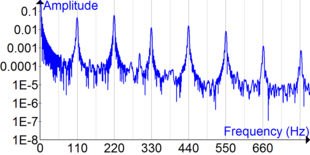
Акустически резонансный объект обычно имеет более одной резонансной частоты, особенно на гармониках самого сильного резонанса. Он будет легко вибрировать на этих частотах и вибрировать менее сильно на других частотах. Он будет «выбирать» свою резонансную частоту из сложного возбуждения, такого как импульс или широкополосное шумовое возбуждение. По сути, он отфильтровывает все частоты, отличные от его резонанса.
Акустический резонанс является важным фактором для создателей инструментов, поскольку большинство акустических инструментов используют резонаторы , такие как струны и корпус скрипки , длина трубки во флейте и форма мембраны барабана. Акустический резонанс также важен для слуха. Например, резонанс жесткого структурного элемента, называемого базилярной мембраной внутри улитки внутреннего уха, позволяет волосковым клеткам на мембране обнаруживать звук. (У млекопитающих мембрана имеет сужающиеся резонансы по всей своей длине, так что высокие частоты концентрируются на одном конце, а низкие частоты — на другом.)
Как и механический резонанс, акустический резонанс может привести к катастрофическому отказу вибратора. Классический пример — разбивание бокала со звуком на точной резонансной частоте бокала.
В музыкальных инструментах натянутые струны, как в лютнях , арфах , гитарах , фортепиано , скрипках и т. д., имеют резонансные частоты, напрямую связанные с массой, длиной и натяжением струны. Длина волны, которая создаст первый резонанс на струне, равна удвоенной длине струны. Более высокие резонансы соответствуют длинам волн, которые являются целыми делениями основной длины волны. Соответствующие частоты связаны со скоростью v волны , движущейся по струне, уравнением
где L — длина струны (для струны, закрепленной на обоих концах), а n = 1, 2, 3... ( Гармоника в трубе с открытым концом (то есть оба конца трубы открыты)). Скорость волны через струну или провод связана с его натяжением T и массой на единицу длины ρ:
Итак, частота связана со свойствами струны уравнением
где T — натяжение , ρ — масса на единицу длины, m — общая масса .
Более высокое натяжение и более короткие длины увеличивают резонансные частоты. Когда струна возбуждается импульсной функцией (щипком пальца или ударом молотка), струна вибрирует на всех частотах, присутствующих в импульсе (импульсная функция теоретически содержит «все» частоты). Те частоты, которые не являются одним из резонансов, быстро отфильтровываются — они ослабляются — и все, что остается, — это гармонические колебания, которые мы слышим как музыкальную ноту.
Резонанс струн происходит на струнных инструментах . Струны или части струн могут резонировать на своих основных или обертонных частотах, когда звучат другие струны. Например, струна A на частоте 440 Гц вызовет резонанс струны E на частоте 330 Гц, поскольку они разделяют обертон 1320 Гц (3-й обертон A и 4-й обертон E).
Резонанс воздушной трубки связан с длиной трубки, ее формой и тем, имеет ли она закрытые или открытые концы. Многие музыкальные инструменты напоминают трубки, которые являются коническими или цилиндрическими (см. отверстие ). Труба, которая закрыта с одного конца и открыта с другого, называется закрытой , в то время как открытая труба открыта с обоих концов. Современные оркестровые флейты ведут себя как открытые цилиндрические трубы; кларнеты ведут себя как закрытые цилиндрические трубы; а саксофоны , гобои и фаготы как закрытые конические трубы, [2] в то время как большинство современных инструментов с губной тростью ( медные духовые инструменты ) акустически похожи на закрытые конические трубы с некоторыми отклонениями (см. педальные тоны и фальшивые тоны ). Подобно струнным, вибрирующие воздушные столбы в идеальных цилиндрических или конических трубах также имеют резонансы на гармониках, хотя есть некоторые различия.
Любой цилиндр резонирует на нескольких частотах, создавая несколько музыкальных тонов. Самая низкая частота называется основной частотой или первой гармоникой. Цилиндры, используемые в качестве музыкальных инструментов, обычно открыты либо с обоих концов, как флейта, либо с одного конца, как некоторые органные трубы. Однако цилиндр, закрытый с обоих концов, также может использоваться для создания или визуализации звуковых волн, как в трубе Рубенса .
Резонансные свойства цилиндра можно понять, рассмотрев поведение звуковой волны в воздухе. Звук распространяется как продольная волна сжатия, заставляя молекулы воздуха двигаться вперед и назад вдоль направления движения. Внутри трубки образуется стоячая волна, длина волны которой зависит от длины трубки. На закрытом конце трубки молекулы воздуха не могут много двигаться, поэтому этот конец трубки является узлом смещения в стоячей волне. На открытом конце трубки молекулы воздуха могут свободно двигаться, создавая пучность смещения . Узлы смещения являются пучностями давления и наоборот.
В таблице ниже показаны волны смещения в цилиндре, закрытом с обоих концов. Обратите внимание, что молекулы воздуха вблизи закрытых концов не могут двигаться, тогда как молекулы вблизи центра трубы движутся свободно. В первой гармонике закрытая труба содержит ровно половину стоячей волны (узел- пучность -узел). Рассматривая волну давления в этой установке, два закрытых конца являются пучностями для изменения давления Δ p ; Следовательно, на обоих концах изменение давления Δ p должно иметь максимальную амплитуду (или удовлетворять ∂(Δp)/∂x = 0 в форме формулировки Штурма–Лиувилля ), что дает уравнение для волны давления: . Интуиция для этого граничного условия ∂(Δp)/∂x = 0 при x = 0 и x = L заключается в том, что давление закрытых концов будет следовать за давлением точки рядом с ними. Применение граничного условия ∂(Δp)/∂x = 0 при x = L дает длины волн стоячих волн:
И резонансные частоты
В цилиндрах с открытыми обоими концами молекулы воздуха вблизи конца свободно перемещаются в трубку и из нее. Это движение создает смещение пучностей в стоячей волне. Узлы имеют тенденцию образовываться внутри цилиндра, вдали от концов. В первой гармонике открытая трубка содержит ровно половину стоячей волны (пучность-узел-пучность). Таким образом, гармоники открытого цилиндра рассчитываются так же, как гармоники закрытого/закрытого цилиндра.
Физика трубы, открытой с обоих концов, объясняется в Physics Classroom. Обратите внимание, что диаграммы в этой ссылке показывают волны смещения, похожие на те, что показаны выше. Они резко контрастируют с волнами давления, показанными ближе к концу настоящей статьи.
Передувая открытую трубу, можно получить ноту, которая на октаву выше основной частоты или ноты трубы. Например, если основная нота открытой трубы — C1, то передувая трубу, можно получить C2, которая на октаву выше C1. [ 3]
Открытые цилиндрические трубки резонируют на приблизительных частотах:
где n — положительное целое число (1, 2, 3...), представляющее узел резонанса, L — длина трубки, а v — скорость звука в воздухе (которая составляет приблизительно 343 метра в секунду [770 миль в час] при 20 °C [68 °F]). Это уравнение исходит из граничных условий для волны давления, которая рассматривает открытые концы как узлы давления, где изменение давления Δ p должно быть равно нулю.
Более точное уравнение, учитывающее коррекцию конца, приведено ниже:
где r — радиус резонансной трубки. Это уравнение компенсирует тот факт, что точная точка, в которой звуковая волна отражается от открытого конца, не находится точно в концевой секции трубки, а находится на небольшом расстоянии снаружи трубки.
Коэффициент отражения немного меньше 1; открытый конец не ведет себя как бесконечно малый акустический импеданс ; скорее, он имеет конечное значение, называемое импедансом излучения, которое зависит от диаметра трубки, длины волны и типа отражающей пластины, возможно, присутствующей вокруг отверстия трубки.
Итак, когда n равно 1:
где v — скорость звука, L — длина резонансной трубы, r — радиус трубы, f — резонансная частота звука, а λ — резонансная длина волны.
При использовании в органе труба, закрытая с одного конца, называется «закрытой трубой». Такие цилиндры имеют основную частоту, но могут быть раздуты для получения других более высоких частот или нот. Эти раздутые регистры можно настраивать, используя различные степени конической конусности. Закрытая труба резонирует на той же основной частоте, что и открытая труба, вдвое длиннее ее, с длиной волны, равной четырем ее длинам. В закрытой трубе узел смещения , или точка отсутствия вибрации, всегда появляется на закрытом конце, и если труба резонирует, она будет иметь пучность смещения , или точку наибольшей вибрации в точке Фи (длина × 0,618) около открытого конца.
Передувая цилиндрическую закрытую трубку, можно получить ноту, которая примерно на двенадцатую выше основной ноты трубки или на квинту выше октавы основной ноты. Например, если основная нота закрытой трубы — C1, то передувая трубку, получаем G2, которая на одну двенадцатую выше C1. В качестве альтернативы мы можем сказать, что G2 на одну пятую выше C2 — октавы выше C1. Регулировка конусности этого цилиндра для уменьшающегося конуса может настроить вторую гармонику или передуваемую ноту близко к положению октавы или 8-й. [4] Открытие небольшого «отверстия динамика» в точке Фи или общей позиции «волна/узел» отменит основную частоту и заставит трубку резонировать на двенадцатой выше основной. Этот прием используется в блокфлейте путем зажимания отверстия для большого пальца на тыльной стороне. Перемещение этого маленького отверстия вверх, ближе к интонации, сделает его "отверстием эха" (модификация блокфлейты Долмеча), которое будет давать точную половинную ноту выше основного тона при открытии. Примечание: для нацеливания на точную частоту половинной ноты необходима небольшая регулировка размера или диаметра. [3]
Закрытая трубка будет иметь приблизительные резонансы:
где "n" здесь нечетное число (1, 3, 5...). Этот тип трубки производит только нечетные гармоники и имеет свою основную частоту на октаву ниже, чем у открытого цилиндра (то есть, половину частоты). Это уравнение исходит из граничных условий для волны давления, которые рассматривают закрытый конец как пучности давления, где изменение давления Δ p должно иметь максимальную амплитуду или удовлетворять ∂(Δp)/∂x = 0 в форме формулировки Штурма–Лиувилля . Интуиция для этого граничного условия ∂(Δp)/∂x = 0 при x = L заключается в том, что давление закрытого конца будет следовать за давлением точки рядом с ним.
Более точное уравнение, учитывающее коррекцию конца, приведено ниже:
Опять же, когда n равно 1:
где v — скорость звука, L — длина резонансной трубы, d — диаметр трубы, f — резонансная частота звука, λ — резонансная длина волны.
На двух диаграммах ниже показаны первые три резонанса волны давления в цилиндрической трубке с пучностями на закрытом конце трубы. На диаграмме 1 трубка открыта с обоих концов. На диаграмме 2 она закрыта с одного конца. Горизонтальная ось — давление. Обратите внимание, что в этом случае открытый конец трубы — узел давления, а закрытый конец — пучность давления.
Открытая коническая труба, то есть труба в форме усеченного конуса с открытыми обоими концами, будет иметь резонансные частоты, приблизительно равные частотам открытой цилиндрической трубы той же длины.
Резонансные частоты остановленной конической трубы — полного конуса или усеченного конуса с одним закрытым концом — удовлетворяют более сложному условию:
где волновое число k равно
и x — расстояние от меньшего конца усеченного конуса до вершины. Когда x мало, то есть когда конус почти полный, это становится
что приводит к резонансным частотам, приблизительно равным частотам открытого цилиндра, длина которого равна L + x . Другими словами, полная коническая труба ведет себя приблизительно как открытая цилиндрическая труба той же длины, и в первом порядке поведение не изменится, если полный конус заменить замкнутым усеченным конусом этого конуса.
Звуковые волны в прямоугольном ящике включают такие примеры, как корпуса громкоговорителей и здания. Прямоугольные здания имеют резонансы, описанные как моды комнаты . Для прямоугольного ящика резонансные частоты определяются как [5]
где v — скорость звука, L x и L y и L z — размеры коробки. , , и — неотрицательные целые числа, которые не могут быть все равны нулю. Если небольшой корпус динамика герметичен, частота достаточно низкая, а компрессия достаточно высокая, звуковое давление (уровень децибел) внутри коробки будет одинаковым в любой точке внутри коробки, это гидравлическое давление.
Резонансная частота жесткой полости статического объема V 0 с суженным звуковым отверстием площадью A и длиной L определяется по формуле резонанса Гельмгольца [6] [7]
где эквивалентная длина шеи с конечной коррекцией
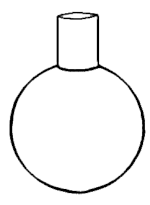
Для сферической полости формула резонансной частоты принимает вид
где
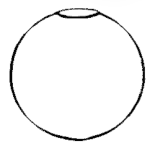
Для сферы, имеющей только звуковое отверстие, L = 0, а поверхность сферы действует как фланец, поэтому
В сухом воздухе при 20 °C, где d и D в метрах, f в герцах , это становится

Это классическая демонстрация резонанса. У стакана есть естественный резонанс, частота, на которой стакан будет легко вибрировать. Поэтому стакан должен быть перемещен звуковой волной на этой частоте. Если сила звуковой волны, заставляющая стакан вибрировать, достаточно велика, размер вибрации станет настолько большим, что стекло треснет. Чтобы сделать это надежно для научной демонстрации, требуется практика и тщательный выбор стакана и громкоговорителя. [9]
Несколько композиторов начали делать резонанс предметом своих композиций. Элвин Люсье использовал акустические инструменты и генераторы синусоидальных волн для исследования резонанса больших и малых объектов во многих своих композициях. Сложные негармонические обертоны выпуклого крещендо и декрещендо на тамтаме или другом ударном инструменте взаимодействуют с резонансами помещения в произведении Джеймса Тенни « Koan: Having Never Written A Note For Percussion» . Полин Оливерос и Стюарт Демпстер регулярно выступают в больших реверберирующих пространствах, таких как цистерна объемом 2 миллиона галлонов США (7600 м3 ) в Форт-Уордене, штат Вашингтон, которая имеет реверберацию с затуханием в 45 секунд. « Терпсихорд » профессора композиции и композитора Академии музыки Мальмё Кента Олофссона , пьеса для ударных и предварительно записанных звуков, [использует] резонансы акустических инструментов [для] формирования звуковых мостов к предварительно записанным электронным звукам, которые, в свою очередь, продлевают резонансы, преобразуя их в новые звуковые жесты». [10]