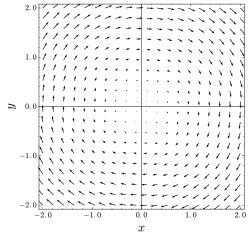
В векторном исчислении соленоидальное векторное поле (также известное как несжимаемое векторное поле , бездивергентное векторное поле или поперечное векторное поле ) — это векторное поле v с нулевой дивергенцией во всех точках поля: Обычный способ выражения этого свойства — сказать, что поле не имеет источников или стоков. [примечание 1]
Теорема о дивергенции дает эквивалентное интегральное определение соленоидального поля, а именно, что для любой замкнутой поверхности суммарный поток через поверхность должен быть равен нулю:
где — внешняя нормаль к каждому элементу поверхности.
Основная теорема векторного исчисления гласит, что любое векторное поле может быть выражено как сумма безвихревого и соленоидального полей. Условие нулевой дивергенции выполняется всякий раз, когда векторное поле v имеет только компоненту векторного потенциала , поскольку определение векторного потенциала A как: автоматически приводит к тождеству (как можно показать, например, с помощью декартовых координат): Обратное также верно: для любого соленоидального v существует векторный потенциал A такой, что (Строго говоря, это выполняется при определенных технических условиях на v , см. разложение Гельмгольца .)
Слово «соленоидальный» происходит от греческого слова σωληνοειδές (sōlēnoeidēs), что означает «трубчатый», от σωλην (sōlēn) или труба.