медиана

Средний квантиль набора данных или распределения вероятностей

Нахождение медианы в наборах данных с нечетным и четным количеством значений.

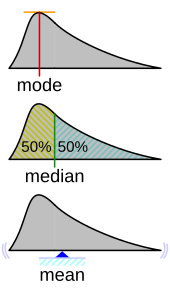
В статистике и теории вероятностей медиана — это значение, отделяющее верхнюю половину от нижней половины выборки данных , совокупности или распределения вероятностей . Для набора данных его можно рассматривать как «среднее» значение. Основная особенность медианы при описании данных по сравнению со средним значением (часто называемым просто «средним») заключается в том, что она не искажается небольшой частью чрезвычайно больших или малых значений и, следовательно, обеспечивает лучшее представление центра. Медианный доход , например, может быть лучшим способом описать центр распределения доходов, поскольку увеличение крупнейших доходов само по себе не влияет на медиану. По этой причине медиана имеет центральное значение в надежной статистике .

Конечный набор данных чисел

Медиана конечного списка чисел — это «среднее» число, когда эти числа перечислены в порядке от наименьшего к наибольшему.

Если набор данных имеет нечетное количество наблюдений, выбирается среднее. Например, следующий список из семи чисел:

1, 3, 3, 6 , 7, 8, 9

имеет медиану 6 , что является четвертым значением.

Если в наборе данных четное количество наблюдений, четкого среднего значения не существует, и медиана обычно определяется как среднее арифметическое двух средних значений. ^{[1] [2]} Например, этот набор данных из 8 чисел

1, 2, 3, 4, 5 , 6, 8, 9

имеет медианное значение 4,5 , т.е. (В более технических терминах медиана интерпретируется как полностью урезанный средний диапазон ). ${\displaystyle (4+5)/2}$

В общем, согласно этому соглашению, медиану можно определить следующим образом: Для набора данных элементов , упорядоченных от наименьшего к наибольшему, ${\displaystyle x}$ ${\displaystyle n}$

если это нечетно, ${\displaystyle n}$ ${\displaystyle \operatorname {med} (x)=x_{(n+1)/2}}$

если четно, ${\displaystyle n}$ ${\displaystyle \operatorname {med} (x)={\frac {x_{(n/2)}+x_{((n/2)+1)}}{2}}}$

Формальное определение и обозначения

Формально медианой популяции является любое значение, при котором по крайней мере половина населения меньше или равна предлагаемой медиане и по крайней мере половина больше или равна предлагаемой медиане. Как видно выше, медианы могут не быть уникальными. Если каждый набор содержит более половины населения, то часть населения в точности равна уникальной медиане.

Медиана четко определена для любых упорядоченных (одномерных) данных и не зависит от какой-либо метрики расстояния . Таким образом, медиану можно применять к школьным классам, которые ранжируются, но не являются числовыми (например, вычисление средней оценки, когда результаты тестов учащихся оцениваются от F до A), хотя результат может быть на полпути между классами, если количество классов четное. . (Для классов с нечетными числами один конкретный класс определяется как медиана.)

С другой стороны, геометрическая медиана определяется в любом количестве измерений. Родственная концепция, в которой результат вынужден соответствовать члену выборки, — это медоид .

Не существует общепринятого стандартного обозначения медианы, но некоторые авторы представляют медиану переменной x как med( x ), x͂ , ^[3] как µ _1/2 , ^[1] или как M . ^{[3] [4]} В любом из этих случаев использование тех или иных символов медианы должно быть явно определено при их введении.

Медиана является частным случаем других способов суммирования типичных значений, связанных со статистическим распределением : это 2-й квартиль , 5-й дециль и 50-й процентиль .

Использование

Медиану можно использовать в качестве меры местоположения , когда экстремальным значениям придается пониженное значение, обычно потому, что распределение искажено , экстремальные значения неизвестны или выбросы не заслуживают доверия, т. е. могут быть ошибками измерения/транскрипции.

Например, рассмотрим мультимножество

1, 2, 2, 2, 3, 14.

В данном случае медиана равна 2, как и мода , и ее можно рассматривать как лучшее указание на центр , чем среднее арифметическое 4, которое больше, чем все значения, кроме одного. Однако широко цитируемая эмпирическая зависимость, согласно которой среднее значение смещается «дальше в хвост» распределения, чем медиана, в целом не соответствует действительности. В лучшем случае можно сказать, что эти две статистики не могут находиться «слишком далеко» друг от друга; см. § Средства и медианы, относящиеся к неравенству, ниже. ^[5]

Поскольку медиана основана на средних данных в наборе, для ее расчета не обязательно знать значение крайних результатов. Например, в психологическом тесте, исследующем время, необходимое для решения проблемы, если небольшому количеству людей вообще не удалось решить проблему за заданное время, все равно можно рассчитать медиану. ^[6]

Поскольку медиану легко понять и легко рассчитать, а также она является надежным приближением к среднему значению , медиана является популярной сводной статистикой в ​​описательной статистике . В этом контексте существует несколько вариантов измерения изменчивости : диапазон , межквартильный диапазон , среднее абсолютное отклонение и медианное абсолютное отклонение .

В практических целях различные показатели местоположения и дисперсии часто сравниваются на основе того, насколько хорошо можно оценить соответствующие значения численности населения на основе выборки данных. Медиана, рассчитанная с использованием выборочной медианы, имеет в этом отношении хорошие свойства. Хотя обычно предполагается, что данное распределение населения не является оптимальным, его свойства всегда достаточно хорошие. Например, сравнение эффективности оценщиков -кандидатов показывает, что выборочное среднее является более статистически эффективным, когда — и только тогда — данные не загрязнены данными из распределений с тяжелым хвостом или из смесей распределений. ^{[ нужна цитация ]} Даже в этом случае эффективность медианы составляет 64% по сравнению со средним значением минимальной дисперсии (для больших нормальных выборок), то есть дисперсия медианы будет на ~ 50% больше, чем дисперсия среднего значения. ^{[7] [8]}

Распределения вероятностей

Геометрическая визуализация моды, медианы и среднего значения произвольной функции плотности вероятности. ^[9]

Для любого действительного распределения вероятностей с кумулятивной функцией распределения  F медиана определяется как любое действительное число  m , которое удовлетворяет неравенствам

$${\displaystyle \int _{(-\infty ,m]}dF(x)\geq {\frac {1}{2}}{\text{ and }}\int _{[m,\infty )}dF(x)\geq {\frac {1}{2}}.}$$

Эквивалентная формулировка использует случайную величину X , распределенную согласно F :

$${\displaystyle \operatorname {P} (X\leq m)\geq {\frac {1}{2}}{\text{ and }}\operatorname {P} (X\geq m)\geq {\frac {1}{2}}}$$

Обратите внимание, что это определение не требует, чтобы X имело абсолютно непрерывное распределение (которое имеет функцию плотности вероятности f ), а также не требует дискретного распределения . В первом случае неравенства можно повысить до равенства: медиана удовлетворяет

$${\displaystyle \operatorname {P} (X\leq m)=\int _{-\infty }^{m}{f(x)\,dx}={\frac {1}{2}}=\int _{m}^{\infty }{f(x)\,dx}=\operatorname {P} (X\geq m).}$$

Любое распределение вероятностей в множестве действительных чисел имеет по крайней мере одну медиану, но в патологических случаях медиан может быть более одной: если F постоянна 1/2 на интервале (так что там f = 0), то любое значение этого интервал является медианой. ${\displaystyle \mathbb {R} }$

Медианы конкретных распределений

Медианы некоторых типов распределений можно легко рассчитать по их параметрам; более того, они существуют даже для некоторых распределений, в которых отсутствует четко определенное среднее значение, таких как распределение Коши :

• Медиана симметричного унимодального распределения совпадает с модой.
• Медиана симметричного распределения , имеющая среднее значение µ, также принимает значение µ .
  • Медиана нормального распределения со средним значением µ и дисперсией σ ² равна µ. Фактически, для нормального распределения среднее = медиана = мода.
  • Медиана равномерного распределения в интервале [ a ,  b ] равна ( a  +  b )/2, что также является средним значением.
• Медиана распределения Коши с параметром местоположения x ₀ и параметром масштаба y равна  x ₀ , параметру местоположения.
• Медиана степенного распределения x ^{- a} с показателем a  > 1 равна 2 ^{1/( a  - 1)} x _min , где x _min - минимальное значение, для которого выполняется степенной закон ^[10]
• Медиана экспоненциального распределения с параметром скорости λ представляет собой натуральный логарифм 2, деленный на параметр скорости: λ ⁻¹ ln 2.
• Медиана распределения Вейбулла с параметром формы k и параметром масштаба λ равна  λ (ln 2) ^{1/ k} .

Характеристики

Свойство оптимальности

Средняя абсолютная ошибка действительной переменной c по отношению к случайной величине  X равна

${\displaystyle E(\left|X-c\right|)\,}$

При условии, что распределение вероятностей X таково, что вышеуказанное ожидание существует, тогда m является медианой X тогда и только тогда, когда m является минимизатором средней абсолютной ошибки по отношению к X . ^[11] В частности, если m является выборочной медианой, то оно минимизирует среднее арифметическое абсолютных отклонений. ^[12] Однако обратите внимание, что в случаях, когда выборка содержит четное количество элементов, этот минимизатор не является уникальным.

В более общем смысле медиана определяется как минимум

${\displaystyle E(|X-c|-|X|),}$

как обсуждается ниже в разделе о многомерных медианах (в частности, пространственной медиане ).

Это основанное на оптимизации определение медианы полезно при статистическом анализе данных, например, при кластеризации k -медиан .

Неравенство, касающееся средних и медиан

Сравнение среднего значения , медианы и моды двух логнормальных распределений с разной асимметрией

Если распределение имеет конечную дисперсию, то расстояние между медианой и средним значением ограничено одним стандартным отклонением . ${\displaystyle {\tilde {X}}}$ ${\displaystyle {\bar {X}}}$

Эта граница была доказана Буком и Шером в 1979 году для дискретных выборок ^[13] и, в более общем плане, Пейджем и Мерти в 1982 году. ^[14] В комментарии к последующему доказательству О'Киннеида ^[15] Маллоуз в 1991 году представил компактное доказательство, дважды использующее неравенство Йенсена , ^[16] следующим образом. Использование |·| для абсолютного значения мы имеем

${\displaystyle {\begin{aligned}|\mu -m|=|\operatorname {E} (X-m)|&\leq \operatorname {E} (|X-m|)\\&\leq \operatorname {E} (|X-\mu |)\\&\leq {\sqrt {\operatorname {E} \left((X-\mu )^{2}\right)}}=\sigma .\end{aligned}}}$

Первое и третье неравенства происходят из неравенства Йенсена, примененного к функции абсолютного значения и квадратичной функции, каждая из которых выпукла. Второе неравенство связано с тем, что медиана минимизирует функцию абсолютного отклонения . ${\displaystyle a\mapsto \operatorname {E} (|X-a|)}$

Доказательство Маллоуза можно обобщить, чтобы получить многомерную версию неравенства ^[17] , просто заменив абсолютное значение нормой :

${\displaystyle \|\mu -m\|\leq {\sqrt {\operatorname {E} \left(\|X-\mu \|^{2}\right)}}={\sqrt {\operatorname {trace} \left(\operatorname {var} (X)\right)}}}$

где m — пространственная медиана , то есть минимизатор функции. Пространственная медиана уникальна, если размерность набора данных равна двум или более. ^{[18] [19]} ${\displaystyle a\mapsto \operatorname {E} (\|X-a\|).\,}$

Альтернативное доказательство использует одностороннее неравенство Чебышева; оно проявляется в неравенстве параметров местоположения и масштаба . Эта формула также следует непосредственно из неравенства Кантелли . ^[20]

Унимодальные распределения

В случае унимодальных распределений можно добиться более четкой границы расстояния между медианой и средним значением:

${\displaystyle \left|{\tilde {X}}-{\bar {X}}\right|\leq \left({\frac {3}{5}}\right)^{\frac {1}{2}}\sigma \approx 0.7746\sigma }$. ^[21]

Аналогичное соотношение сохраняется между медианой и модой:

${\displaystyle \left|{\tilde {X}}-\mathrm {mode} \right|\leq 3^{\frac {1}{2}}\sigma \approx 1.732\sigma .}$

Неравенство Дженсена для медиан

Неравенство Йенсена утверждает, что для любой случайной величины X с конечным математическим ожиданием E [ X ] и для любой выпуклой функции f

${\displaystyle f[E(x)]\leq E[f(x)]}$

Это неравенство распространяется и на медиану. Мы говорим, что функция f : R → R является функцией C , если для любого t

${\displaystyle f^{-1}\left(\,(-\infty ,t]\,\right)=\{x\in \mathbb {R} \mid f(x)\leq t\}}$

является замкнутым интервалом (допускающим вырожденные случаи одной точки или пустого множества ). Каждая выпуклая функция является функцией C, но обратное неверно. Если f — функция C, то

${\displaystyle f(\operatorname {med} [X])\leq \operatorname {med} [f(X)]}$

Если медианы не единственны, утверждение справедливо для соответствующих супремумов. ^[22]

Медианы для выборок

Эффективное вычисление медианы выборки

Несмотря на то, что для сортировки сравнения n элементов требуется Ω ( n log n ) операций, алгоритмы выбора могут вычислить k -й наименьший из n элементов только с помощью Θ ( n ) операций. Сюда входит медиана, т.н/2статистика-го порядка (или для четного числа выборок среднее арифметическое двух статистик среднего порядка). ^[23]

Алгоритмы отбора по-прежнему имеют недостаток: они требуют памяти Ω( n ) , то есть им необходимо иметь в памяти полную выборку (или ее линейную часть). Поскольку это, а также требование линейного времени может быть непомерно высоким, было разработано несколько процедур оценки медианы. Простым является правило медианы трех элементов, которое оценивает медиану как медиану подвыборки из трех элементов; это обычно используется как подпрограмма в алгоритме быстрой сортировки, который использует оценку медианы входных данных. Более надежная оценка — это девятое правило Тьюки , которое представляет собой медиану трех правил, применяемых с ограниченной рекурсией: ^[24] если A — это выборка, представленная в виде массива , и

med3( А ) = med( А [1], А [н/2], А [ н ]) ,

затем

девятый( А ) = med3(med3( A [1 ...1/3n ]), med3( A [1/3н ...2/3n ]), med3( A [2/3н ... н ]))

Медиана — это средство оценки медианы, которое требует линейного времени, но сублинейной памяти и работает за один проход по выборке. ^[25]

Выборочное распределение

Распределение выборочного среднего и выборочной медианы было определено Лапласом . ^[26] Распределение выборочной медианы из популяции с функцией плотности асимптотически нормально со средним значением и дисперсией ^[27] ${\displaystyle f(x)}$ ${\displaystyle \mu }$

${\displaystyle {\frac {1}{4nf(m)^{2}}}}$

где – медиана и – размер выборки: ${\displaystyle m}$ ${\displaystyle f(x)}$ ${\displaystyle n}$

${\displaystyle {\text{Sample median}}\sim {\mathcal {N}}\left(\mu =m,\sigma ^{2}={\frac {1}{4nf(m)^{2}}}\right)}$

Современное доказательство следует ниже. Результат Лапласа теперь понимается как частный случай асимптотического распределения произвольных квантилей .

Для нормальных выборок плотность равна , поэтому для больших выборок дисперсия медианы равна ^[7] (см. также раздел #Эффективность ниже). ${\displaystyle f(m)=1/{\sqrt {2\pi \sigma ^{2}}}}$ ${\displaystyle ({\pi }/{2})\cdot (\sigma ^{2}/n).}$

Вывод асимптотического распределения

Мы принимаем размер выборки за нечетное число и предполагаем, что наша переменная непрерывна; формула для случая дискретных переменных приведена ниже в § Эмпирическая локальная плотность. Выборку можно резюмировать как «ниже медианы», «на уровне медианы» и «выше медианы», что соответствует трехчленному распределению с вероятностями , и . Для непрерывной переменной вероятность того, что несколько значений выборки будут точно равны медиане, равна 0, поэтому можно вычислить плотность в точке непосредственно из триномиального распределения: ${\displaystyle N=2n+1}$ ${\displaystyle F(v)}$ ${\displaystyle f(v)}$ ${\displaystyle 1-F(v)}$ ${\displaystyle v}$

${\displaystyle \Pr[\operatorname {med} =v]\,dv={\frac {(2n+1)!}{n!n!}}F(v)^{n}(1-F(v))^{n}f(v)\,dv}$.

Теперь мы вводим бета-функцию. Для целочисленных аргументов и это можно выразить как . Также напомним об этом . Использование этих отношений и установка обоих и равных позволяет записать последнее выражение как ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle \mathrm {B} (\alpha ,\beta )={\frac {(\alpha -1)!(\beta -1)!}{(\alpha +\beta -1)!}}}$ ${\displaystyle f(v)\,dv=dF(v)}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$ ${\displaystyle n+1}$

${\displaystyle {\frac {F(v)^{n}(1-F(v))^{n}}{\mathrm {B} (n+1,n+1)}}\,dF(v)}$

Следовательно, функция плотности медианы представляет собой симметричное бета-распределение, выдвинутое вперед на . Его среднее значение, как и следовало ожидать, равно 0,5, а дисперсия — 0,000 . По правилу цепочки соответствующая дисперсия выборочной медианы равна ${\displaystyle F}$ ${\displaystyle 1/(4(N+2))}$

${\displaystyle {\frac {1}{4(N+2)f(m)^{2}}}}$.

Дополнительные 2 в пределе пренебрежимо малы .

Эмпирическая локальная плотность

На практике функции и выше часто неизвестны или не предполагаются. Однако их можно оценить по наблюдаемому распределению частот. В этом разделе мы приведем пример. Рассмотрим следующую таблицу, представляющую выборку из 3800 (дискретных) наблюдений: ${\displaystyle f}$ ${\displaystyle F}$

Поскольку наблюдения имеют дискретные значения, построение точного распределения медианы не является немедленным переводом приведенного выше выражения для ; можно (и обычно имеет) иметь несколько экземпляров медианы в выборке. Итак, мы должны суммировать все эти возможности: ${\displaystyle \Pr(\operatorname {med} =v)}$

${\displaystyle \Pr(\operatorname {med} =v)=\sum _{i=0}^{n}\sum _{k=0}^{n}{\frac {N!}{i!(N-i-k)!k!}}F(v-1)^{i}(1-F(v))^{k}f(v)^{N-i-k}}$

Здесь i — количество точек, строго меньшее медианы, а k — число, строго большее.

Используя эти предварительные сведения, можно исследовать влияние размера выборки на стандартные ошибки среднего и медианы. Наблюдаемое среднее значение составляет 3,16, наблюдаемая необработанная медиана — 3, а наблюдаемая интерполированная медиана — 3,174. В следующей таблице приведены некоторые сравнительные статистические данные.

Ожидаемое значение медианы немного падает по мере увеличения размера выборки, в то время как, как и следовало ожидать, стандартные ошибки как медианы, так и среднего значения пропорциональны обратному квадратному корню из размера выборки. Асимптотическая аппроксимация ошибочна, поскольку переоценивает стандартную ошибку.

Оценка дисперсии на основе выборочных данных

Значение — асимптотическое значение где — медиана населения — изучалось несколькими авторами. Стандартный метод складного ножа «удалить один» дает противоречивые результаты. ^[28] Было показано , что альтернативный метод — метод «удаления k», растущий с размером выборки, асимптотически непротиворечив. ^[29] Этот метод может быть дорогостоящим в вычислительном отношении для больших наборов данных. Бутстрап-оценка, как известно, непротиворечива ^[30] , но сходится очень медленно ( порядка ). ^[31] Были предложены и другие методы, но их поведение может различаться в зависимости от больших и малых выборок. ^[32] ${\displaystyle (2f(x))^{-2}}$ ${\displaystyle n^{-1/2}(\nu -m)}$ ${\displaystyle \nu }$ ${\displaystyle k}$ ${\displaystyle n^{-{\frac {1}{4}}}}$

Эффективность

Эффективность выборочной медианы, измеряемая как отношение дисперсии среднего значения к дисперсии медианы, зависит от размера выборки и основного распределения населения . Для выборки размера нормального распределения эффективность при больших N равна ${\displaystyle N=2n+1}$

${\displaystyle {\frac {2}{\pi }}{\frac {N+2}{N}}}$

КПД стремится к бесконечности. ${\displaystyle {\frac {2}{\pi }}}$ ${\displaystyle N}$

Другими словами, относительная дисперсия медианы будет на 57% больше, чем дисперсия среднего значения, а относительная стандартная ошибка медианы будет на 25% больше, чем стандартная ошибка среднего значения (см. также раздел #Распределение выборки выше.). ^[33] ${\displaystyle \pi /2\approx 1.57}$ ${\displaystyle (\pi /2)^{\frac {1}{2}}\approx 1.25}$ ${\displaystyle \sigma /{\sqrt {n}}}$

Другие оценщики

Для одномерных распределений, симметричных относительно одной медианы, оценка Ходжеса-Лемана является надежной и высокоэффективной оценкой медианы совокупности. ^[34]

Если данные представлены статистической моделью , определяющей конкретное семейство распределений вероятностей , то оценки медианы можно получить путем подгонки этого семейства распределений вероятностей к данным и расчета теоретической медианы подобранного распределения. ^{[ нужна цитата ]} Интерполяция Парето является применением этого подхода, когда предполагается, что население имеет распределение Парето .

Многомерная медиана

Ранее в этой статье обсуждалась одномерная медиана, когда выборка или совокупность были одномерными. Когда размерность равна двум или выше, существует несколько концепций, расширяющих определение одномерной медианы; каждая такая многомерная медиана согласуется с одномерной медианой, когда размерность равна ровно единице. ^{[34] [35] [36] [37]}

Маргинальная медиана

Маргинальная медиана определяется для векторов, определенных относительно фиксированного набора координат. Маргинальная медиана определяется как вектор, компоненты которого являются одномерными медианами. Маргинальную медиану легко вычислить, ее свойства изучались Пури и Сеном ^{[34] [38]}

Геометрическая медиана

Геометрическая медиана дискретного набора точек выборки в евклидовом пространстве — это точка ^[a] , минимизирующая сумму расстояний до точек выборки. ${\displaystyle x_{1},\ldots x_{N}}$

${\displaystyle {\hat {\mu }}={\underset {\mu \in \mathbb {R} ^{m}}{\operatorname {arg\,min} }}\sum _{n=1}^{N}\left\|\mu -x_{n}\right\|_{2}}$

В отличие от маргинальной медианы, геометрическая медиана эквивариантна относительно евклидовых преобразований подобия, таких как сдвиги и повороты .

Медиана во всех направлениях

Если маргинальные медианы для всех систем координат совпадают, то их общее расположение можно назвать «медианой во всех направлениях». ^[40] Эта концепция актуальна для теории голосования на основании теоремы о медианном избирателе . Когда она существует, медиана по всем направлениям совпадает с геометрической медианой (по крайней мере, для дискретных распределений).

Центральная точка

В статистике и вычислительной геометрии понятие центральной точки является обобщением медианы для данных в многомерном евклидовом пространстве . Учитывая набор точек в d -мерном пространстве, центральной точкой набора является такая точка, что любая гиперплоскость, проходящая через эту точку, делит набор точек на два примерно равных подмножества: меньшая часть должна иметь как минимум 1/( d  +1) доля баллов. Как и медиана, центральная точка не обязательно должна быть одной из точек данных. Каждый непустой набор точек (без дубликатов) имеет хотя бы одну центральную точку.

Другие концепции, связанные с медианой

Интерполированная медиана

Имея дело с дискретной переменной, иногда полезно рассматривать наблюдаемые значения как средние точки лежащих в их основе непрерывных интервалов. Примером этого является шкала Лайкерта , в которой мнения или предпочтения выражаются по шкале с заданным количеством возможных ответов. Если шкала состоит из целых положительных чисел, наблюдение, равное 3, можно рассматривать как представляющее интервал от 2,50 до 3,50. Можно оценить медиану базовой переменной. Если, скажем, 22% наблюдений имеют значение 2 или ниже, а 55,0% — значение 3 или ниже (то есть 33% имеют значение 3), то медиана равна 3, поскольку медиана — это наименьшее значение, для которого больше чем половина. Но интерполированная медиана находится где-то между 2,50 и 3,50. Сначала мы добавляем половину ширины интервала к медиане, чтобы получить верхнюю границу медианного интервала. Затем мы вычитаем ту долю ширины интервала, которая равна доле 33%, лежащей выше отметки 50%. Другими словами, мы делим ширину интервала пропорционально количеству наблюдений. В этом случае 33% делятся на 28% ниже медианы и 5% выше нее, поэтому мы вычитаем 5/33 ширины интервала от верхней границы 3,50, чтобы получить интерполированную медиану 3,35. Более формально, если значения известны, интерполированную медиану можно рассчитать по формуле ${\displaystyle m}$ ${\displaystyle x}$ ${\displaystyle F(x)}$ ${\displaystyle w}$ ${\displaystyle f(x)}$

${\displaystyle m_{\text{int}}=m+w\left[{\frac {1}{2}}-{\frac {F(m)-{\frac {1}{2}}}{f(m)}}\right].}$

Альтернативно, если в наблюдаемой выборке есть баллы выше медианной категории, баллы в ней и баллы ниже нее, то интерполированная медиана определяется как ${\displaystyle k}$ ${\displaystyle j}$ ${\displaystyle i}$

${\displaystyle m_{\text{int}}=m+{\frac {w}{2}}\left[{\frac {k-i}{j}}\right].}$

Псевдомедиана

Для одномерных распределений, симметричных относительно одной медианы, оценка Ходжеса-Лемана является надежной и высокоэффективной оценкой медианы совокупности; для несимметричных распределений оценка Ходжеса-Лемана является надежной и высокоэффективной оценкой псевдомедианы популяции , которая является медианой симметричного распределения и близка к медиане популяции. ^[41] Оценка Ходжеса-Лемана была обобщена на многомерные распределения. ^[42]

Варианты регрессии

Оценщик Тейла -Сена — это метод устойчивой линейной регрессии , основанный на нахождении медиан наклонов . ^[43]

Медианный фильтр

Медианный фильтр — важный инструмент обработки изображений , который может эффективно удалять любые шумы соли и перца из изображений в оттенках серого .

Кластерный анализ

В кластерном анализе алгоритм кластеризации k-медиан обеспечивает способ определения кластеров, в котором критерий максимизации расстояния между кластерными средними, который используется при кластеризации k-средних , заменяется максимизацией расстояния между кластерными медианами.

Срединная – срединная линия

Это метод робастной регрессии. Идея восходит к Вальду в 1940 году, который предложил разделить набор двумерных данных на две половины в зависимости от значения независимого параметра : левую половину со значениями меньше медианы и правую половину со значениями больше медианы. ^[44] Он предложил взять средние значения зависимых и независимых переменных левой и правой половин и оценить наклон линии, соединяющей эти две точки. Затем линию можно было бы скорректировать, чтобы она соответствовала большинству точек в наборе данных. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle x}$

Наир и Шривастава в 1942 году предложили аналогичную идею, но вместо этого предложили разделить выборку на три равные части перед расчетом средних значений подвыборок. ^[45] Браун и Муд в 1951 году предложили идею использования медиан двух подвыборок, а не средних значений. ^[46] Тьюки объединил эти идеи и рекомендовал разделить выборку на три подвыборки одинакового размера и оценить линию на основе медиан подвыборок. ^[47]

Медианно-несмещенные оценки

Любая несмещенная к среднему оценка минимизирует риск ( ожидаемые потери ) по отношению к функции потерь квадратичной ошибки , как заметил Гаусс . Медианно - несмещенная оценка минимизирует риск относительно функции потерь абсолютного отклонения , как заметил Лаплас . Другие функции потерь используются в статистической теории , особенно в робастной статистике .

Теория несмещенных по медиане оценок была возрождена Джорджем Брауном в 1947 году: ^[48]

Оценка одномерного параметра θ будет называться несмещенной по медиане, если при фиксированном θ медиана распределения оценки равна значению θ; т. е. оценка занижается так же часто, как и переоценивается. Кажется, что для большинства целей это требование удовлетворяет тем же требованиям, что и требование несмещенности по среднему, и обладает дополнительным свойством, состоящим в том, что оно инвариантно относительно взаимно однозначного преобразования.

—  стр. 584

Сообщалось о других свойствах несмещенных по медиане оценок. ^{[49] [50] [51] [52]} Медианно-несмещенные оценки инвариантны относительно взаимно-однозначных преобразований .

Существуют методы построения несмещенных по медиане оценок, которые являются оптимальными (в смысле, аналогичном свойству минимальной дисперсии для оценок, несмещенных по среднему). Такие конструкции существуют для распределений вероятностей, имеющих монотонные функции правдоподобия . ^{[53] [54]} Одна из таких процедур является аналогом процедуры Рао-Блэквелла для несмещенных в среднем оценок: процедура справедлива для меньшего класса распределений вероятностей, чем процедура Рао-Блэквелла, но для большего класса функций потерь . ^[55]

История

Научные исследователи на древнем Ближнем Востоке, похоже, вообще не использовали сводную статистику, вместо этого выбирая значения, которые обеспечивали максимальную согласованность с более широкой теорией, объединяющей широкий спектр явлений. ^[56] В средиземноморском (а позднее и европейском) научном сообществе статистика, подобная среднему значению, по своей сути является развитием Средневековья и раннего Нового времени. (История медианы за пределами Европы и ее предшественников остается относительно неизученной.)

Идея медианы появилась в VI веке в Талмуде для справедливого анализа расхождений в оценках . ^{[57] [58]} Однако эта концепция не распространилась на более широкое научное сообщество.

Вместо этого ближайшим предком современной медианы является средний диапазон , изобретенный Аль-Бируни ^{[59] : 31  [60].} Передача его работы более поздним ученым неясна. Он применил свою технику для анализа валютных металлов, но после того, как он опубликовал свою работу, большинство пробирщиков по-прежнему принимали самые неблагоприятные значения из своих результатов, чтобы не создать впечатление обмана . ^{[59] : 35–8  [61]} Однако рост мореплавания в эпоху Великих географических открытий означал, что штурманам кораблей все чаще приходилось пытаться определить широту в неблагоприятную погоду относительно враждебных берегов, что привело к возобновлению интереса к сводной статистике. Независимо от того, открыт ли он заново или изобретен независимо, средний диапазон рекомендован морским мореплавателям в «Инструкциях по путешествию Рэли в Гвиану» Харриота, 1595 год. ^{[59] : 45–8}

Идея медианы, возможно, впервые появилась в книге Эдварда Райта 1599 года «Определенные ошибки в навигации» в разделе, посвященном навигации по компасу . ^[62] Райт не хотел отбрасывать измеренные значения и, возможно, считал, что медиана, включающая большую часть набора данных, чем средний диапазон , с большей вероятностью будет правильной. Однако Райт не привел примеров использования своей техники, из-за чего было трудно проверить, описал ли он современное понятие медианы. ^{[56] [60] [b]} Медиана (в контексте вероятности) конечно фигурировала в переписке Христиана Гюйгенса , но как пример статистики, неподходящей для актуарной практики . ^[56]

Самая ранняя рекомендация о медиане датируется 1757 годом, когда Роджер Джозеф Боскович разработал метод регрессии, основанный на норме L 1 и, следовательно, неявно на медиане. ^{[56] [63]} В 1774 году Лаплас ясно выразил это желание: он предложил использовать медиану в качестве стандартной оценки значения апостериорной PDF . Конкретным критерием была минимизация ожидаемой величины ошибки; где оценка и истинное значение. С этой целью Лаплас определил распределение как выборочного среднего, так и выборочной медианы в начале 1800-х годов. ^{[26] [64]} Однако десять лет спустя Гаусс и Лежандр разработали метод наименьших квадратов , который минимизирует для получения среднего значения. В контексте регрессии нововведение Гаусса и Лежандра значительно упрощает вычисления. Следовательно, предложение Лапласа в целом отвергалось до тех пор, пока 150 лет спустя не появились вычислительные устройства (и это до сих пор относительно необычный алгоритм). ^[65] ${\displaystyle |\alpha -\alpha ^{*}|}$ ${\displaystyle \alpha ^{*}}$ ${\displaystyle \alpha }$ ${\displaystyle (\alpha -\alpha ^{*})^{2}}$

Антуан Огюстен Курно в 1843 году был первым ^[66] , кто использовал термин медиана ( valeur médiane ) для значения, которое делит распределение вероятностей на две равные половины. Густав Теодор Фехнер использовал медиану ( Centralwerth ) в социологических и психологических явлениях. ^[67] Ранее он использовался только в астрономии и смежных областях. Густав Фехнер популяризировал медиану в формальном анализе данных, хотя ранее она использовалась Лапласом ^[67] , а медиана появилась в учебнике Ф. Я. Эджворта . ^[68] Фрэнсис Гальтон использовал английский термин « медиана» в 1881 году, ^{[69] [70]} ранее использовал термины «среднее значение» в 1869 году и « среднее» в 1880 году ^{. [71] [72]}

Статистики на протяжении всего XIX века активно поощряли использование медиан из-за их интуитивной ясности. Однако понятие медианы не поддается теории высших моментов так же, как среднее арифметическое , и его гораздо труднее вычислить. В результате в течение 20 века медиана как понятие общего среднего значения постепенно вытеснялась средним арифметическим. ^{[56] [60]}

Смотрите также

• Математический портал

• Абсолютное отклонение  - разница между наблюдаемым значением переменной и эталонным значением.Pages displaying short descriptions of redirect targets
• Смещение оценщика  - разница между ожидаемым значением оценщика и истинным значением параметра.
• Центральная тенденция  – статистическое значение, представляющее центр или среднее значение распределения.
• Концентрация меры  – Статистический параметр для функций Липшица  – Сильная форма равномерной непрерывностиPages displaying short descriptions of redirect targets
• Медианный граф  - график с медианой для каждых трех вершин.
• Медиана медиан  - Быстрый алгоритм аппроксимации медианы - Алгоритм расчета приблизительной медианы за линейное время.
• Медианный поиск  - метод поиска k-го наименьшего значения.Pages displaying short descriptions of redirect targets
• Медианный наклон  – статистический метод подбора линии.Pages displaying short descriptions of redirect targets
• Теория медианного избирателя  - Теория в политологииPages displaying short descriptions of redirect targets
• Медоид  – репрезентативные объекты набора данных или кластера внутри набора данных, сумма различий которых со всеми объектами в кластере минимальна. Pages displaying wikidata descriptions as a fallbacks – Обобщение медианы в более высоких измерениях.

Примечания

1. Геометрическая медиана уникальна, если выборка не коллинеарна. ^[39]
2. Последующие ученые, похоже, согласились с Эйзенхартом в том, что цифры Бороза за 1580 год, хотя и наводят на мысль о медиане, на самом деле описывают среднее арифметическое; ^{[59] :} Районы 62–3 не упоминаются ни в одной другой работе.

Рекомендации

1. Вайсштейн, Эрик В. «Статистическая медиана». Математический мир .
2. Саймон, Лаура Дж.; «Описательная статистика». Архивировано 30 июля 2010 г. в Wayback Machine , Набор ресурсов для статистического образования , Департамент статистики штата Пенсильвания.
3. Дерек Бисселл (1994). Статистические методы для Spc и Tqm. ЦРК Пресс. стр. 26–. ISBN 978-0-412-39440-9. Проверено 25 февраля 2013 г.
4. Дэвид Дж. Шескин (27 августа 2003 г.). Справочник по параметрическим и непараметрическим статистическим процедурам (Третье изд.). ЦРК Пресс. п. 7. ISBN 978-1-4200-3626-8. Проверено 25 февраля 2013 г.
5. Пол Т. фон Хиппель (2005). «Среднее, медиана и перекос: исправление правила из учебника». Журнал статистического образования . 13 (2). Архивировано из оригинала 14 октября 2008 г. Проверено 18 июня 2015 г.
6. Робсон, Колин (1994). Эксперимент, дизайн и статистика в психологии . Пингвин. стр. 42–45. ISBN 0-14-017648-9.
7. Уильямс, Д. (2001). Взвешивание шансов . Издательство Кембриджского университета. п. 165. ИСБН 052100618X.
8. Мейндональд, Джон; Браун, В. Джон (6 мая 2010 г.). Анализ данных и графика с использованием R: подход на основе примеров. Издательство Кембриджского университета. п. 104. ИСБН 978-1-139-48667-5.
9. «Обзор статистики AP - кривые плотности и нормальное распределение» . Архивировано из оригинала 8 апреля 2015 года . Проверено 16 марта 2015 г.
10. Ньюман, MEJ (2005). «Степенные законы, распределения Парето и закон Ципфа». Современная физика . 46 (5): 323–351. arXiv : cond-mat/0412004 . Бибкод : 2005ConPh..46..323N. дои : 10.1080/00107510500052444. S2CID  2871747.
11. Строк, Дэниел (2011). Теория вероятности . Издательство Кембриджского университета. стр. 43. ISBN 978-0-521-13250-3.
12. ДеГрут, Моррис Х. (1970). Оптимальные статистические решения. McGraw-Hill Book Co., Нью-Йорк-Лондон-Сидней. п. 232. ИСБН 9780471680291. МР  0356303.
13. Книга Стивена А.; Лоуренс Шер (1979). «Насколько близки среднее и медиана?». Двухлетний математический журнал колледжа . 10 (3): 202–204. дои : 10.2307/3026748. JSTOR  3026748 . Проверено 12 марта 2022 г.
14. Уоррен Пейдж; Ведула Н. Мурти (1982). «Отношения близости между мерами центральной тенденции и дисперсии: Часть 1». Двухлетний математический журнал колледжа . 13 (5): 315–327. doi : 10.1080/00494925.1982.11972639 (неактивен 31 января 2024 г.) . Проверено 12 марта 2022 г.{{cite journal}}: CS1 maint: DOI inactive as of January 2024 (link)
15. О'Синнеид, Колм Арт (1990). «Среднее значение находится в пределах одного стандартного отклонения от любой медианы». Американский статистик . 44 (4): 292–293. дои : 10.1080/00031305.1990.10475743 . Проверено 12 марта 2022 г.
16. Маллоуз, Колин (август 1991 г.). «Еще один комментарий к О'Синнеиду». Американский статистик . 45 (3): 257. дои : 10.1080/00031305.1991.10475815.
17. Пише, Роберт (2012). Случайные векторы и случайные последовательности . Академическое издательство Ламберта. ISBN 978-3659211966.
18. Кемперман, Йоханнес HB (1987). Додж, Ядола (ред.). «Медиана конечной меры в банаховом пространстве: статистический анализ данных на основе L1-нормы и связанных с ней методов». Материалы первой международной конференции, проходившей в Невшателе 31 августа – 4 сентября 1987 г. Амстердам: Издательство Северной Голландии: 217–230. МР  0949228.
19. Миласевич, Филипп; Дюшарм, Жиль Р. (1987). «Единственность пространственной медианы». Анналы статистики . 15 (3): 1332–1333. дои : 10.1214/aos/1176350511 . МР  0902264.
20. К.Ван Стин Заметки о вероятности и статистике
21. Басу, С.; Дасгупта, А. (1997). «Среднее, медиана и режим унимодальных распределений: характеристика». Теория вероятностей и ее приложения . 41 (2): 210–223. дои : 10.1137/S0040585X97975447. S2CID  54593178.
22. Меркл, М. (2005). «Неравенство Дженсена для медиан». Статистика и вероятностные буквы . 71 (3): 277–281. дои : 10.1016/j.spl.2004.11.010.
23. Альфред В. Ахо, Джон Э. Хопкрофт и Джеффри Д. Ульман (1974). Проектирование и анализ компьютерных алгоритмов . Ридинг/Массачусетс: Аддисон-Уэсли. ISBN 0-201-00029-6.Здесь: Раздел 3.6 «Статистика заказов», стр.97-99, в частности Алгоритм 3.6 и Теорема 3.9.
24. Бентли, Джон Л.; Макилрой, М. Дуглас (1993). «Разработка функции сортировки». Программное обеспечение: практика и опыт . 23 (11): 1249–1265. дои : 10.1002/спе.4380231105. S2CID  8822797.
25. Руссиу, Питер Дж.; Бассетт, Гилберт В. младший (1990). «Ремедиан: надежный метод усреднения для больших наборов данных» (PDF) . Дж. Амер. Статист. доц . 85 (409): 97–104. дои : 10.1080/01621459.1990.10475311.
26. Стиглер, Стивен (декабрь 1973 г.). «Исследования по истории вероятности и статистики. XXXII: Лаплас, Фишер и открытие концепции достаточности». Биометрика . 60 (3): 439–445. дои : 10.1093/биомет/60.3.439. JSTOR  2334992. MR  0326872.
27. Райдер, Пол Р. (1960). «Разница медианы небольших выборок из нескольких особых групп населения». Дж. Амер. Статист. доц. 55 (289): 148–150. дои : 10.1080/01621459.1960.10482056.
28. Эфрон, Б. (1982). Складной нож, Bootstrap и другие планы повторной выборки . Филадельфия: СИАМ. ISBN 0898711797.
29. Шао, Дж.; Ву, CF (1989). «Общая теория оценки дисперсии складного ножа». Анна. Стат. 17 (3): 1176–1197. дои : 10.1214/aos/1176347263 . JSTOR  2241717.
30. Эфрон, Б. (1979). «Методы начальной загрузки: еще один взгляд на складной нож». Анна. Стат. 7 (1): 1–26. дои : 10.1214/aos/1176344552 . JSTOR  2958830.
31. Холл, П.; Мартин, Массачусетс (1988). «Точная скорость сходимости бутстрап-оценщика квантильной дисперсии». Области, связанные с теорией вероятностей . 80 (2): 261–268. дои : 10.1007/BF00356105 . S2CID  119701556.
32. Хименес-Гамеро, доктор медицины; Муньос-Гарсия, Ж.; Пино-Мехиас, Р. (2004). «Уменьшенная начальная загрузка для медианы». Статистика Синица . 14 (4): 1179–1198.
33. Мейндональд, Джон; Джон Браун, В. (6 мая 2010 г.). Анализ данных и графика с использованием R: подход на основе примеров. Издательство Кембриджского университета. ISBN 9781139486675.
34. Хеттманспергер, Томас П.; Маккин, Джозеф В. (1998). Робастные непараметрические статистические методы . Статистическая библиотека Кендалла. Том. 5. Лондон: Эдвард Арнольд. ISBN 0-340-54937-8. МР  1604954.
35. Смолл, Кристофер Г. «Обзор многомерных медиан». Международное статистическое обозрение/Международное статистическое обозрение (1990): 263–277. дои : 10.2307/1403809 JSTOR  1403809
36. Ниинимаа, А. и Х. Оя. «Многомерная медиана». Энциклопедия статистических наук (1999).
37. Мослер, Карл. Многомерная дисперсия, центральные регионы и глубина: подход зоноида подъема. Том. 165. Springer Science & Business Media, 2012.
38. Пури, Мадан Л.; Сен, Пранаб К.; Непараметрические методы в многомерном анализе , John Wiley & Sons, Нью-Йорк, 1971. (Перепечатано Krieger Publishing)
39. Варди, Иегуда; Чжан, Цунь-Хуэй (2000). «Многомерная L1-медиана и связанная с ней глубина данных». Труды Национальной академии наук Соединенных Штатов Америки . 97 (4): 1423–1426 (электронный). Бибкод : 2000PNAS...97.1423V. дои : 10.1073/pnas.97.4.1423 . МР  1740461. ПМК 26449 . ПМИД  10677477. 
40. Дэвис, Отто А.; ДеГрут, Моррис Х.; Хинич, Мелвин Дж. (январь 1972 г.). «Порядок социальных предпочтений и правило большинства» (PDF) . Эконометрика . 40 (1): 147–157. дои : 10.2307/1909727. JSTOR  1909727.Авторы, работающие в теме, в которой предполагается уникальность, фактически используют выражение « уникальная медиана во всех направлениях».
41. Пратт, Уильям К.; Купер, Тед Дж.; Кабир, Ихтишам (11 июля 1985 г.). Корбетт, Фрэнсис Дж (ред.). «Псевдомедианный фильтр». Архитектуры и алгоритмы цифровой обработки изображений II . 0534 : 34. Бибкод : 1985SPIE..534...34P. дои : 10.1117/12.946562. S2CID  173183609.
42. Оджа, Ханну (2010). Многомерные непараметрические методы с  R : подход, основанный на пространственных знаках и рангах . Конспект лекций по статистике. Том. 199. Нью-Йорк, штат Нью-Йорк: Спрингер. стр. xiv+232. дои : 10.1007/978-1-4419-0468-3. ISBN 978-1-4419-0467-6. МР  2598854.
43. Уилкокс, Рэнд Р. (2001), «Оценщик Тейла – Сена», Основы современных статистических методов: существенное повышение мощности и точности, Springer-Verlag, стр. 207–210, ISBN 978-0-387-95157-7.
44. Уолд, А. (1940). «Подбор прямых линий, если обе переменные подвержены ошибкам» (PDF) . Анналы математической статистики . 11 (3): 282–300. дои : 10.1214/aoms/1177731868 . JSTOR  2235677.
45. Наир, КР; Шривастава, депутат парламента (1942). «О простом методе подбора кривой». Санкхья: Индийский статистический журнал . 6 (2): 121–132. JSTOR  25047749.
46. Браун, GW; Настроение, А.М. (1951). «О медианных тестах линейных гипотез». Материалы Второго симпозиума Беркли по математической статистике и теории вероятностей . Беркли, Калифорния: Издательство Калифорнийского университета. стр. 159–166. Збл  0045.08606.
47. Тьюки, JW (1977). Исследовательский анализ данных. Ридинг, Массачусетс: Аддисон-Уэсли. ISBN 0201076160.
48. Браун, Джордж В. (1947). «О маловыборочном оценивании». Анналы математической статистики . 18 (4): 582–585. дои : 10.1214/aoms/1177730349 . JSTOR  2236236.
49. Леманн, Эрих Л. (1951). «Общая концепция беспристрастности». Анналы математической статистики . 22 (4): 587–592. дои : 10.1214/aoms/1177729549 . JSTOR  2236928.
50. Бирнбаум, Аллан (1961). «Единая теория оценки, I». Анналы математической статистики . 32 (1): 112–135. дои : 10.1214/aoms/1177705145 . JSTOR  2237612.
51. ван дер Ваарт, Х. Роберт (1961). «Некоторые расширения идеи предвзятости». Анналы математической статистики . 32 (2): 436–447. дои : 10.1214/aoms/1177705051 . JSTOR  2237754. MR  0125674.
52. Пфанзагль, Иоганн; при содействии Р. Хамбокера (1994). Параметрическая статистическая теория . Вальтер де Грюйтер. ISBN 3-11-013863-8. МР  1291393.
53. Пфанцагль, Иоганн. «Об оптимальных медианных несмещенных оценках при наличии мешающих параметров». Анналы статистики (1979): 187–193.
54. Браун, LD; Коэн, Артур; Стродерман, МЫ (1976). «Теорема о полном классе для строгого монотонного отношения правдоподобия с приложениями». Анна. Статист . 4 (4): 712–722. дои : 10.1214/aos/1176343543 .
55. Страница; Браун, Л.Д.; Коэн, Артур; Стродерман, МЫ (1976). «Теорема о полном классе для строгого монотонного отношения правдоподобия с приложениями». Анна. Статист . 4 (4): 712–722. дои : 10.1214/aos/1176343543 .
56. Баккер, Артур; Гравемейер, Коено ЧП (1 июня 2006 г.). «Историческая феноменология среднего и медианы». Образовательные исследования по математике . 62 (2): 149–168. дои : 10.1007/s10649-006-7099-8. ISSN  1573-0816. S2CID  143708116.
57. Адлер, Дэн (31 декабря 2014 г.). «Талмуд и современная экономика». Еврейские американские и израильские проблемы . Архивировано из оригинала 6 декабря 2015 года . Проверено 22 февраля 2020 г. .
58. Современная экономическая теория в Талмуде Исраэля Ауманна
59. Эйзенхарт, Черчилль (24 августа 1971 г.). Развитие понятия о наилучшем средстве совокупности измерений от древности до наших дней (PDF) (Выступление). 131-е ежегодное собрание Американской статистической ассоциации. Государственный университет Колорадо.
60. «Как средний показатель победил медианный». Ценаономика . 5 апреля 2016 года . Проверено 23 февраля 2020 г.
61. Сангстер, Алан (март 2021 г.). «Жизнь и творчество Луки Пачоли (1446/7–1517), педагога-гуманиста». Абак . 57 (1): 126–152. дои : 10.1111/abac.12218. hdl : 2164/16100 . ISSN  0001-3072. S2CID  233917744.
62. Райт, Эдвард; Парсонс, EJS; Моррис, ВФ (1939). «Эдвард Райт и его работа». Имаго Мунди . 3 : 61–71. дои : 10.1080/03085693908591862. ISSN  0308-5694. JSTOR  1149920.
63. Стиглер, С.М. (1986). История статистики: измерение неопределенности до 1900 года. Издательство Гарвардского университета. ISBN 0674403401.
64. Лаплас PS de (1818) Deuxième Supplement à la Théorie Analytique des Probabilités , Париж, Courcier
65. Джейнс, ET (2007). Теория вероятностей: логика науки (5-е печатное изд.). Кембридж [ua]: Cambridge Univ. Нажимать. п. 172. ИСБН 978-0-521-59271-0.
66. Ховарт, Ричард (2017). Словарь математических наук о Земле: с историческими примечаниями . Спрингер. п. 374.
67. Кейнс, Дж. М. (1921) Трактат о вероятности . Pt II Ch XVII §5 (стр. 201) (переиздание 2006 г., Cosimo Classics, ISBN 9781596055308  : несколько других переизданий) 
68. Стиглер, Стивен М. (2002). Статистика на столе: история статистических концепций и методов. Издательство Гарвардского университета. стр. 105–7. ISBN 978-0-674-00979-0.
69. Гальтон Ф. (1881) «Отчет Антропометрического комитета», стр. 245–260. Отчет 51-го собрания Британской ассоциации содействия развитию науки
70. Дэвид, HA (1995). «Первое (?) появление общих терминов в математической статистике». Американский статистик . 49 (2): 121–133. дои : 10.2307/2684625. ISSN  0003-1305. JSTOR  2684625.
71. энциклопедияofmath.org
72. личный.psu.edu

Внешние ссылки

• «Медиана (в статистике)», Математическая энциклопедия , EMS Press , 2001 [1994]
• Медиана как среднее арифметическое всех выборочных наблюдений.
• Он-лайн калькулятор
• Расчет медианы
• Проблема, связанная со средним значением, медианой и модой.
• Вайсштейн, Эрик В. «Статистическая медиана». Математический мир .
• Скрипт Python для расчета медианы и показателей неравенства доходов
• Быстрое вычисление медианы путем последовательного группирования
• «Среднее, медиана, мода и асимметрия». Учебное пособие, разработанное для студентов-психологов первого курса Оксфордского университета на основе проработанного примера.
• Сложная математическая задача SAT Даже совет колледжа ошибся: Эндрю Дэниелс в «Популярной механике»

В эту статью включены материалы из дистрибутива Median на PlanetMath , который распространяется по лицензии Creative Commons Attribution/Share-Alike License .