stringtranslate.com

Сферическая упаковка

Сферическая упаковка находит практическое применение при укладке пушечных ядер .

В геометрии упаковка сфер — это расположение непересекающихся сфер внутри вмещающего пространства. Рассматриваемые сферы обычно имеют одинаковый размер, а пространство обычно представляет собой трехмерное евклидово пространство . Однако проблемы упаковки сфер можно обобщить, чтобы рассмотреть неравные сферы, пространства других измерений (где проблема становится упаковкой кругов в двух измерениях или упаковкой гиперсфер в более высоких измерениях) или неевклидовыми пространствами, такими как гиперболическое пространство .

Типичная проблема упаковки сфер — найти такое расположение, при котором сферы заполнят как можно большую часть пространства. Доля пространства, заполненного сферами, называется плотностью упаковки устройства. Поскольку локальная плотность упаковки в бесконечном пространстве может меняться в зависимости от объема, в котором она измеряется, проблема обычно состоит в том, чтобы максимизировать среднюю или асимптотическую плотность , измеренную в достаточно большом объеме.

Для равных сфер в трех измерениях самая плотная упаковка занимает примерно 74% объема. Случайная упаковка равных сфер обычно имеет плотность около 63,5%. [1]

Классификация и терминология

Решётчатое расположение (обычно называемое регулярным расположением) — это такое расположение, в котором центры сфер образуют очень симметричный узор, для однозначного определения которого требуется только n векторов (в n - мерном евклидовом пространстве ). Решеточные расположения являются периодическими. Компоновки, в которых сферы не образуют решетку (часто называемые нерегулярными ), все же могут быть периодическими, но также апериодическими (собственно говоря, непериодическими ) или случайными . Из-за высокой степени симметрии решетчатые упаковки легче классифицировать, чем нерешетчатые. Периодические решетки всегда имеют четко определенную плотность.

Регулярная упаковка

Правильное расположение равных сфер на плоскости сменяется неправильным расположением неравных сфер (пузырей).
Решетка HCP (слева) и решетка FCC (справа) являются двумя наиболее распространенными схемами с самой высокой плотностью.
Два способа сложить три плоскости из сфер

Плотная упаковка

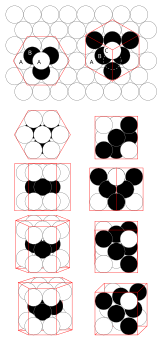
В трехмерном евклидовом пространстве наиболее плотная упаковка равных сфер достигается за счет семейства структур, называемых плотноупакованными структурами. Один из способов создания такой структуры заключается в следующем. Рассмотрим плоскость, на которой компактно расположены сферы. Назовем ее А. Для любых трех соседних сфер четвертую сферу можно разместить сверху в полости между тремя нижними сферами. Если мы сделаем это для половины отверстий во второй плоскости над первой, мы создадим новый компактный слой. Есть два возможных варианта сделать это, назовем их B и C. Предположим, что мы выбрали B. Тогда одна половина впадин B лежит над центрами шаров в A, а другая половина лежит над впадинами A, которые не были используется для B. Таким образом, шары третьего слоя могут быть размещены либо непосредственно над шарами первого слоя, давая слой типа А, либо над отверстиями первого слоя, которые не были заняты вторым слоем, давая слой типа C. Объединение слоев типов A, B и C дает различные плотноупакованные структуры.

Два простых расположения внутри плотноупакованного семейства соответствуют регулярным решеткам. Один из них называется кубической плотной упаковкой (или гранецентрированной кубической «FCC») — где слои чередуются в последовательности ABCABC…. Другой называется плотной гексагональной упаковкой («HCP»), где слои чередуются в последовательности ABAB…. [ сомнительно - обсудить ] Но возможны многие последовательности наложения слоев (ABAC, ABCBA, ABCBAC и т. д.), и они все равно создают плотноупакованную структуру. Во всех этих устройствах каждая сфера касается 12 соседних сфер [2] , а средняя плотность равна

В 1611 году Иоганн Кеплер предположил, что это максимально возможная плотность как среди правильных, так и среди нерегулярных расположений — это стало известно как гипотеза Кеплера . Карл Фридрих Гаусс в 1831 году доказал, что эти упаковки имеют наибольшую плотность среди всех возможных решетчатых упаковок. [3] В 1998 году Томас Каллистер Хейлз , следуя подходу, предложенному Ласло Фейешем Тотом в 1953 году, объявил о доказательстве гипотезы Кеплера. Доказательство Хейлза — это исчерпывающее доказательство , включающее проверку множества отдельных случаев с использованием сложных компьютерных вычислений. Судьи заявили, что они «на 99% уверены» в правильности доказательства Хейлза. 10 августа 2014 года Хейлз объявил о завершении формального доказательства с использованием автоматической проверки доказательств , что устранило любые сомнения. [4]

Другие распространенные решетчатые упаковки

В физических системах часто встречаются и другие решетчатые упаковки. К ним относятся кубическая решетка с плотностью , гексагональная решетка с плотностью и тетраэдрическая решетка с плотностью , а также максимально рыхлая решетка с плотностью 0,0555. [5]

Зажатые насадки низкой плотности

Упаковки, в которых все сферы удерживаются своими соседями в одном месте, называются жесткими или зажатыми . Строго зажатая упаковка сфер с наименьшей плотностью представляет собой разбавленный («туннельный») ГЦК-кристалл с плотностью всего 0,49365. [6]

Нестандартная упаковка

Если мы попытаемся построить плотно упакованную совокупность сфер, у нас возникнет искушение всегда помещать следующую сферу в полость между тремя упакованными сферами. Если пять сфер собраны таким образом, они будут соответствовать одной из регулярно упакованных композиций, описанных выше. Однако шестая сфера, размещенная таким образом, сделает структуру несовместимой с каким-либо регулярным расположением. Это приводит к возможности случайной плотной упаковки сфер, устойчивой к сжатию. [7] Вибрация случайной рыхлой упаковки может привести к упорядочению сферических частиц в регулярные упаковки — процесс, известный как гранулярная кристаллизация . Такие процессы зависят от геометрии контейнера, в котором находятся сферические зерна. [2]

Когда сферы случайным образом добавляются в контейнер, а затем сжимаются, они обычно образуют так называемую «нерегулярную» или «застрявшую» конфигурацию упаковки, когда их больше нельзя сжимать. Эта неравномерная упаковка обычно будет иметь плотность около 64%. Недавние исследования аналитически предсказывают, что плотность не может превысить предел плотности в 63,4% [8]. Эта ситуация отличается от случая одного или двух измерений, когда сжатие набора одномерных или двухмерных сфер (то есть отрезков прямых или кругов) ) даст обычную упаковку.

Упаковка гиперсферы

Задача об упаковке сфер — это трехмерная версия класса задач об упаковке шаров в произвольных измерениях. В двух измерениях эквивалентной проблемой является упаковка кругов на плоскости. В одном измерении это упаковка сегментов линий в линейную вселенную. [9]

В размерностях больше трех известны наиболее плотные решетчатые упаковки гиперсфер до восьми измерений. [10] Очень мало известно о неправильных упаковках гиперсфер; возможно, что в некоторых измерениях самая плотная упаковка может быть нерегулярной. Некоторое подтверждение этой гипотезы дает тот факт, что в некоторых измерениях (например, 10) самая плотная известная неправильная упаковка плотнее, чем самая плотная известная регулярная упаковка. [11]

В 2016 году Марина Вязовская объявила о доказательстве того, что решетка E 8 обеспечивает оптимальную упаковку (независимо от регулярности) в восьмимерном пространстве [12] , а вскоре после этого она и группа соавторов анонсировали аналогичное доказательство того, что решетка Лича оптимальна. в 24 измерениях. [13] Этот результат основан на улучшенных предыдущих методах, которые показали, что эти две решетки очень близки к оптимальным. [14] Новые доказательства включают использование преобразования Лапласа тщательно выбранной модулярной функции для построения радиально симметричной функции f такой, что f и ее преобразование Фурье f̂ оба равны 1 в начале координат и оба обращаются в нуль во всех других точках оптимальной решетки. , с отрицательным f вне центральной сферы упаковки и положительным f̂ . Затем формула суммирования Пуассона для f используется для сравнения плотности оптимальной решетки с плотностью любой другой упаковки. [15] Еще до того, как доказательство было официально рассмотрено и опубликовано, математик Питер Сарнак назвал его «потрясающе простым» и написал: «Вы просто начинаете читать статью и знаете, что это правильно». [16]

Другое направление исследований в области больших размерностей — попытка найти асимптотические границы плотности самых плотных упаковок. Известно, что при больших n плотность самой плотной решетки в размерности n находится между cn ⋅ 2 − n (для некоторой константы c ) и 2 −(0,599+o(1)) n . [17] Гипотетические границы лежат посередине. [18] В 2023 году в препринте Марсело Кампоса, Мэтью Йенссена, Маркуса Мишлена и Джулиана Сахасрабуде была улучшена нижняя граница максимальной плотности до [19]

Неравная упаковка сфер

Плотная упаковка сфер с отношением радиусов 0,64799 и плотностью 0,74786 [20]

Многие проблемы в химических и физических науках могут быть связаны с проблемами упаковки, когда доступно более одного размера сферы. Здесь есть выбор между разделением сфер на области плотноупакованных равных сфер или объединением сфер разных размеров в сложную или промежуточную упаковку. Когда доступно множество размеров сфер (или распределение ), проблема быстро становится неразрешимой, но доступны некоторые исследования бинарных твердых сфер (два размера).

Когда вторая сфера намного меньше первой, можно расположить большие сферы плотно упакованными, а затем расположить малые сферы внутри октаэдрических и тетраэдрических промежутков. Плотность этой промежуточной упаковки сильно зависит от соотношения радиусов, но в пределе экстремальных соотношений размеров более мелкие сферы могут заполнять промежутки с той же плотностью, что и более крупные сферы, заполняющие пространство. [21] Даже если большие сферы не расположены плотно, всегда можно вставить несколько меньших сфер с радиусом до 0,29099 радиуса большей сферы. [22]

Когда меньшая сфера имеет радиус, превышающий 0,41421 радиуса большей сферы, она уже не может вписаться даже в октаэдрические отверстия плотноупакованной структуры. Таким образом, за пределами этой точки либо структура-хозяин должна расшириться, чтобы вместить межузельные элементы (что ставит под угрозу общую плотность), либо перестроиться в более сложную структуру кристаллического соединения. Известны структуры, превышающие плотность плотной упаковки для отношений радиусов до 0,659786. [20] [23]

Также получены верхние оценки плотности, которые можно получить в таких бинарных упаковках. [24]

Во многих химических ситуациях, таких как ионные кристаллы , стехиометрия ограничивается зарядами составляющих ионов. Это дополнительное ограничение на упаковку вместе с необходимостью минимизировать кулоновскую энергию взаимодействующих зарядов приводит к разнообразию оптимальных схем упаковки.

Гиперболическое пространство

Хотя концепцию кругов и сфер можно распространить на гиперболическое пространство , найти самую плотную упаковку становится гораздо сложнее. В гиперболическом пространстве нет ограничений на количество сфер, которые могут окружать другую сферу (например, круги Форда можно рассматривать как совокупность одинаковых гиперболических кругов, в которых каждый круг окружен бесконечным числом других кругов). Понятие средней плотности также становится гораздо труднее дать точное определение. Самые плотные упаковки в любом гиперболическом пространстве почти всегда нерегулярны. [25]

Несмотря на эту трудность, К. Бёречки дает универсальную верхнюю оценку плотности упаковок сфер гиперболического n -пространства, где n  ≥ 2. [26] В трех измерениях граница Бёречки составляет примерно 85,327613% и реализуется упаковкой орисферы тетраэдрические соты 6-го порядка с символом Шлефли {3,3,6}. [27] В дополнение к этой конфигурации известно, что в гиперболическом трехмерном пространстве существуют по крайней мере три другие упаковки орисфер , которые реализуют верхнюю границу плотности. [28]

Касающиеся пары, тройки и четверки.

Контактным графом произвольной конечной упаковки единичных шаров называется граф, вершины которого соответствуют элементам упаковки и две вершины которого соединены ребром, если соответствующие два элемента упаковки касаются друг друга. Мощность множества ребер контактного графа дает количество соприкасающихся пар, количество 3-циклов в контактном графе дает количество соприкасающихся троек, а количество тетраэдров в контактном графе дает количество соприкасающихся четверок ( в общем случае для контактного графа, связанного с упаковкой сфер в n измерениях, мощность набора n -симплексов в контактном графе дает количество соприкасающихся ( n  + 1)-кортежей в упаковке сфер). В случае трехмерного евклидова пространства нетривиальные верхние оценки числа соприкасающихся пар, троек и четверок [29] были доказаны Кароли Бездеком и Сэмюэлем Ридом в Университете Калгари.

Проблема поиска расположения n одинаковых сфер, обеспечивающего максимальное количество точек соприкосновения между сферами, известна как «задача липкой сферы». Максимум известен для n ≤ 11, а для больших n известны только предполагаемые значения . [30]

Другие помещения

Упаковка сфер по углам гиперкуба (с сферами, определяемыми расстоянием Хэмминга ) соответствует разработке кодов, исправляющих ошибки : если сферы имеют радиус t , то их центры являются кодовыми словами (2 t  + 1)-кода, исправляющего ошибки. . Решётчатые упаковки соответствуют линейным кодам. Существуют и другие, более тонкие связи между упаковкой евклидовых сфер и кодами, исправляющими ошибки. Например, двоичный код Голея тесно связан с 24-мерной решеткой Лича.

Более подробную информацию об этих соединениях можно найти в книге Конвея и Слоана « Сферические упаковки, решетки и группы» . [31]

Смотрите также

Рекомендации

  1. ^ Ву, Югонг; Фань, Чжиган; Лу, Ючжу (1 мая 2003 г.). «Объемная и внутренняя плотность упаковки случайной плотной упаковки твердых сфер». Журнал материаловедения . 38 (9): 2019–2025. дои : 10.1023/А: 1023597707363. ISSN  1573-4803. S2CID  137583828.
  2. ^ Аб Дай, Вэйцзин; Рейманн, Йорг; Ханаор, Дориан; Ферреро, Клаудио; Ган, Исян (13 марта 2019 г.). «Режимы пристеночной зернистой кристаллизации в вибрационной упаковке». Гранулированная материя . 21 (2): 26. arXiv : 1805.07865 . дои : 10.1007/s10035-019-0876-8. ISSN  1434-7636. S2CID  254106945.
  3. ^ Гаус, CF (1831). «Обсуждение книги Л. А. Сибера: Исследования характеристик положительных троичных квадратичных форм и т. д.» Göttingsche Gelehrte Anzeigen .
  4. ^ «Долгосрочное хранилище для хостинга проектов Google Code» . Архив кода Google .
  5. ^ "Мир математики Вольфрама, упаковка сферы" .
  6. ^ Торквато, С .; Стиллингер, Ф.Х. (2007). «К порогу застревания сферических упаковок: туннелированные кристаллы». Журнал прикладной физики . 102 (9): 093511–093511–8. arXiv : 0707.4263 . Бибкод : 2007JAP...102i3511T. дои : 10.1063/1.2802184. S2CID  5704550.
  7. ^ Чайкин, Пол (июнь 2007 г.). "Случайные мысли". Физика сегодня . Американский институт физики. 60 (6): 8. Бибкод :2007ФТ....60ф...8С. дои : 10.1063/1.2754580. ISSN  0031-9228.
  8. ^ Песня, К.; Ван, П.; Максе, ХА (29 мая 2008 г.). «Фазовая диаграмма застрявшего вещества». Природа . 453 (7195): 629–632. arXiv : 0808.2196 . Бибкод : 2008Natur.453..629S. дои : 10.1038/nature06981. PMID  18509438. S2CID  4420652.
  9. ^ Гриффит, Дж. С. (1962). «Упаковка равных 0-сфер». Природа . 196 (4856): 764–765. Бибкод : 1962Natur.196..764G. дои : 10.1038/196764a0. S2CID  4262056.
  10. ^ Вайсштейн, Эрик В. «Упаковка гиперсферы». Математический мир .
  11. ^ Слоан, NJA (1998). «Проблема упаковки сфер». Документа Математика . 3 : 387–396. arXiv : math/0207256 . Бибкод : 2002math......7256S.
  12. ^ Вязовская, Марина (1 января 2017 г.). «Задача упаковки сфер в размерности 8». Анналы математики . 185 (3): 991–1015. arXiv : 1603.04246 . дои : 10.4007/анналы.2017.185.3.7. ISSN  0003-486X. S2CID  119286185.
  13. ^ Кон, Генри; Кумар, Абхинав; Миллер, Стивен; Радченко Даниил; Вязовская, Марина (1 января 2017 г.). «Задача упаковки сфер в размерности 24». Анналы математики . 185 (3): 1017–1033. arXiv : 1603.06518 . дои :10.4007/анналы.2017.185.3.8. ISSN  0003-486X. S2CID  119281758.
  14. ^ Кон, Генри; Кумар, Абхинав (2009), «Оптимальность и уникальность решетки Лича среди решеток», Annals of Mathematics , 170 (3): 1003–1050, arXiv : math.MG/0403263 , doi :10.4007/annals.2009.170.1003, ISSN  1939-8980, MR  2600869, S2CID  10696627, Збл  1213.11144 Кон, Генри; Кумар, Абхинав (2004), «Самая плотная решетка в двадцати четырех измерениях», Электронные объявления об исследованиях Американского математического общества , 10 (7): 58–67, arXiv : math.MG/0408174 , Bibcode : 2004math... ...8174C, doi :10.1090/S1079-6762-04-00130-1, ISSN  1079-6762, MR  2075897, S2CID  15874595
  15. ^ Миллер, Стивен Д. (4 апреля 2016 г.), Решение проблемы упаковки сфер в 24 измерениях с помощью модульных форм, Институт перспективных исследований , заархивировано из оригинала 21 декабря 2021 г.. Видео часового выступления одного из соавторов Вязовской, объясняющего новые доказательства.
  16. ↑ Кларрайх, Эрика (30 марта 2016 г.), «Упаковка сфер решена в более высоких измерениях», журнал Quanta
  17. ^ Кон, Генри (2017), «Концептуальный прорыв в упаковке сфер» (PDF) , Уведомления Американского математического общества , 64 (2): 102–115, arXiv : 1611.01685 , doi : 10.1090/noti1474, ISSN  0002-9920 , МР  3587715, S2CID  16124591
  18. ^ Торквато, С.; Стиллингер, Ф. Х. (2006), «Новые гипотетические нижние границы оптимальной плотности сферических упаковок», Experimental Mathematics , 15 (3): 307–331, arXiv : math/0508381 , doi : 10.1080/10586458.2006.10128964, MR  2264469, S2CID  9921359
  19. ^ Кампос, Марсело; Дженссен, Мэтью; Мишлен, Маркус; Сахасрабуде, Джулиан (2023). «Новая нижняя граница упаковки сфер». arXiv : 2312.10026 [math.MG].
  20. ^ Аб О'Тул, ИП; Хадсон, Т.С. (2011). «Новые упаковки высокой плотности бинарных сфер одинакового размера». Журнал физической химии C. 115 (39): 19037. doi :10.1021/jp206115p.
  21. ^ Хадсон, ДР (1949). «Плотность и упаковка в совокупности смешанных сфер». Журнал прикладной физики . 20 (2): 154–162. Бибкод : 1949JAP....20..154H. дои : 10.1063/1.1698327.
  22. ^ Зонг, К. (2002). «От глубоких ям к свободным плоскостям». Бюллетень Американского математического общества . 39 (4): 533–555. дои : 10.1090/S0273-0979-02-00950-3 .
  23. ^ Маршалл, GW; Хадсон, Т.С. (2010). «Плотные бинарные упаковки сфер». Вклад в алгебру и геометрию . 51 (2): 337–344.
  24. ^ де Лаат, Дэвид; де Оливейра Фильо, Фернандо Мариу; Валлентин, Франк (12 июня 2012 г.). «Верхние оценки для упаковок сфер нескольких радиусов». Форум математики, Сигма . 2 . arXiv : 1206.2608 . дои : 10.1017/fms.2014.24. S2CID  11082628.
  25. ^ Боуэн, Л.; Радин, К. (2002). «Самая плотная упаковка равных сфер в гиперболическом пространстве». Дискретная и вычислительная геометрия . 29 : 23–39. дои : 10.1007/s00454-002-2791-7 .
  26. ^ Бёрочки, К. (1978). «Упаковка сфер в пространствах постоянной кривизны». Acta Mathematica Academiae Scientiarum Hungaricae . 32 (3–4): 243–261. дои : 10.1007/BF01902361. S2CID  122561092.
  27. ^ Бёрочки, К.; Флориан, А. (1964). «Über die dichteste Kugelpackung im Hyperbolischen Raum». Acta Mathematica Academiae Scientiarum Hungaricae . 15 (1–2): 237–245. дои : 10.1007/BF01897041. S2CID  122081239.
  28. ^ Козьма, RT; Ширмаи, Дж. (2012). «Оптимально плотные упаковки для полностью асимптотических разбиений Кокстера оришарами разных типов». Монашефте по математике . 168 : 27–47. arXiv : 1007.0722 . doi : 10.1007/s00605-012-0393-x. S2CID  119713174.
  29. ^ Бездек, Кароли; Рид, Сэмюэл (2013). «Возвращение к контактным графам сферических упаковок». Журнал геометрии . 104 (1): 57–83. arXiv : 1210.5756 . дои : 10.1007/s00022-013-0156-4. S2CID  14428585.
  30. ^ «Наука о липких сферах». Американский учёный . 6 февраля 2017 года . Проверено 14 июля 2020 г.
  31. ^ Конвей, Джон Х .; Слоан, Нил Дж. А. (1998). Сферические упаковки, решетки и группы (3-е изд.). Springer Science & Business Media. ISBN 0-387-98585-9.

Библиография

Внешние ссылки

Нетехнический обзор упаковки в гиперболическом пространстве.