Обычные наименьшие квадраты

Метод оценки неизвестных параметров в модели линейной регрессии

В статистике обычный метод наименьших квадратов ( OLS ) — это тип линейного метода наименьших квадратов для выбора неизвестных параметров в модели линейной регрессии (с фиксированными эффектами первого уровня ^{[ необходимы пояснения ]} линейной функции набора объясняющих переменных ) путем принцип наименьших квадратов : минимизация суммы квадратов разностей между наблюдаемой зависимой переменной (значениями наблюдаемой переменной) во входном наборе данных и выходом (линейной) функции независимой переменной .

Геометрически это рассматривается как сумма квадратов расстояний, параллельных оси зависимой переменной, между каждой точкой данных в наборе и соответствующей точкой на поверхности регрессии — чем меньше различия, тем лучше модель соответствует данным. . Полученную оценку можно выразить простой формулой, особенно в случае простой линейной регрессии , в которой в правой части уравнения регрессии находится один регрессор .

Оценка OLS согласована для фиксированных эффектов первого уровня, когда регрессоры экзогенны , и формирует идеальную коллинеарность (условие ранга), согласованную для оценки дисперсии остатков, когда регрессоры имеют конечные четвертые моменты ^[1] и - по формуле Гаусса – Маркова Теорема — оптимальная в классе линейных несмещенных оценок, когда ошибки гомоскедастичны и серийно некоррелированы . В этих условиях метод МНК обеспечивает несмещенную оценку с минимальной дисперсией, когда ошибки имеют конечные дисперсии . При дополнительном предположении, что ошибки обычно распределяются с нулевым средним значением, OLS является оценщиком максимального правдоподобия , который превосходит любой нелинейный несмещенный оценщик.

Линейная модель

Закон Оукена в макроэкономике гласит, что в экономике рост ВВП должен линейно зависеть от изменения уровня безработицы. Здесь обычным методом наименьших квадратов строится линия регрессии, описывающая этот закон.

Предположим, данные состоят из наблюдений . Каждое наблюдение включает в себя скалярный отклик и вектор-столбец параметров (регрессоров), т.е. В модели линейной регрессии переменная отклика является линейной функцией регрессоров: ${\displaystyle n}$ ${\displaystyle \left\{\mathbf {x} _{i},y_{i}\right\}_{i=1}^{n}}$ ${\displaystyle i}$ ${\displaystyle y_{i}}$ ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle p}$ ${\displaystyle \mathbf {x} _{i}=\left[x_{i1},x_{i2},\dots ,x_{ip}\right]^{\operatorname {T} }}$ ${\displaystyle y_{i}}$

${\displaystyle y_{i}=\beta _{1}\ x_{i1}+\beta _{2}\ x_{i2}+\cdots +\beta _{p}\ x_{ip}+\varepsilon _{i},}$

или в векторной форме,

${\displaystyle y_{i}=\mathbf {x} _{i}^{\operatorname {T} }{\boldsymbol {\beta }}+\varepsilon _{i},\,}$

где , как было введено ранее, представляет собой вектор-столбец -го наблюдения всех независимых переменных; – вектор неизвестных параметров; а скаляр представляет ненаблюдаемые случайные величины ( ошибки ) -го наблюдения. учитывает влияние на ответы источников, отличных от объясняющих переменных . Эту модель также можно записать в матричной записи как ${\displaystyle \mathbf {x} _{i}}$ ${\displaystyle i}$ ${\displaystyle {\boldsymbol {\beta }}}$ ${\displaystyle p\times 1}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle i}$ ${\displaystyle \varepsilon _{i}}$ ${\displaystyle y_{i}}$ ${\displaystyle \mathbf {x} _{i}}$

${\displaystyle \mathbf {y} =\mathbf {X} {\boldsymbol {\beta }}+{\boldsymbol {\varepsilon }},\,}$

где и — векторы переменных ответа и ошибок наблюдений , а — матрица регрессоров, также иногда называемая матрицей плана , строка которой является и содержит -е наблюдения по всем объясняющим переменным. ${\displaystyle \mathbf {y} }$ ${\displaystyle {\boldsymbol {\varepsilon }}}$ ${\displaystyle n\times 1}$ ${\displaystyle n}$ ${\displaystyle \mathbf {X} }$ ${\displaystyle n\times p}$ ${\displaystyle i}$ ${\displaystyle \mathbf {x} _{i}^{\operatorname {T} }}$ ${\displaystyle i}$

Обычно в набор регрессоров включают постоянный член , скажем, взяв за все . Коэффициент , соответствующий этому регрессору, называется интерцептом . Без пересечения подобранная линия вынуждена пересечь начало координат, когда . ${\displaystyle \mathbf {X} }$ ${\displaystyle x_{i1}=1}$ ${\displaystyle i=1,\dots ,n}$ ${\displaystyle \beta _{1}}$ ${\displaystyle x_{i}={\vec {0}}}$

Регрессоры не обязательно должны быть независимыми, чтобы оценка была последовательной, но мультиколлинеарность делает оценку непоследовательной. В качестве конкретного примера, когда регрессоры не являются независимыми, мы могли бы предположить, что отклик линейно зависит как от значения, так и от его квадрата; в этом случае мы бы включили один регрессор, значение которого равно квадрату другого регрессора. В этом случае модель будет квадратичной по второму регрессору, но, тем не менее, по-прежнему считается линейной моделью, поскольку модель по-прежнему линейна по параметрам ( ). ${\displaystyle {\boldsymbol {\beta }}}$

Матричная/векторная формулировка

Рассмотрим переопределенную систему

${\displaystyle \sum _{j=1}^{p}x_{ij}\beta _{j}=y_{i},\ (i=1,2,\dots ,n),}$

линейных уравнений с неизвестными коэффициентами , , при . Это можно записать в матричной форме как ${\displaystyle n}$ ${\displaystyle p}$ ${\displaystyle \beta _{1},\beta _{2},\dots ,\beta _{p}}$ ${\displaystyle n>p}$

${\displaystyle \mathbf {X} {\boldsymbol {\beta }}=\mathbf {y} ,}$

где

${\displaystyle \mathbf {X} ={\begin{bmatrix}X_{11}&X_{12}&\cdots &X_{1p}\\X_{21}&X_{22}&\cdots &X_{2p}\\\vdots &\vdots &\ddots &\vdots \\X_{n1}&X_{n2}&\cdots &X_{np}\end{bmatrix}},\qquad {\boldsymbol {\beta }}={\begin{bmatrix}\beta _{1}\\\beta _{2}\\\vdots \\\beta _{p}\end{bmatrix}},\qquad \mathbf {y} ={\begin{bmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{bmatrix}}.}$

(Примечание: для линейной модели, описанной выше, не все элементы содержат информацию о точках данных. Первый столбец заполняется единицами. Только остальные столбцы содержат фактические данные. Таким образом, здесь равно количеству регрессоров плюс один) . ${\displaystyle \mathbf {X} }$ ${\displaystyle X_{i1}=1}$ ${\displaystyle p}$

Такая система обычно не имеет точного решения, поэтому вместо этого цель состоит в том, чтобы найти коэффициенты, которые «наилучшим образом» соответствуют уравнениям в смысле решения задачи квадратичной минимизации . ${\displaystyle {\boldsymbol {\beta }}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}={\underset {\boldsymbol {\beta }}{\operatorname {arg\,min} }}\,S({\boldsymbol {\beta }}),}$

где целевая функция определяется выражением ${\displaystyle S}$

${\displaystyle S({\boldsymbol {\beta }})=\sum _{i=1}^{n}\left|y_{i}-\sum _{j=1}^{p}X_{ij}\beta _{j}\right|^{2}=\left\|\mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\right\|^{2}.}$

Обоснование выбора этого критерия приведено в разделе «Свойства» ниже. Эта задача минимизации имеет единственное решение при условии, что столбцы матрицы линейно независимы , определяемое решением так называемых нормальных уравнений : ${\displaystyle p}$ ${\displaystyle \mathbf {X} }$

${\displaystyle \left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right){\hat {\boldsymbol {\beta }}}=\mathbf {X} ^{\operatorname {T} }\mathbf {y} \ .}$

Матрица известна как нормальная матрица или матрица Грама , а матрица известна как матрица моментов регресса и регрессоров. ^[2] Наконец, вектор коэффициентов гиперплоскости наименьших квадратов , выраженный как ${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {X} }$ ${\displaystyle \mathbf {X} ^{\operatorname {T} }\mathbf {y} }$ ${\displaystyle {\hat {\boldsymbol {\beta }}}}$

${\displaystyle {\hat {\boldsymbol {\beta }}}=\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }\mathbf {y} .}$

или

${\displaystyle {\hat {\boldsymbol {\beta }}}={\boldsymbol {\beta }}+\left(\mathbf {X} ^{\operatorname {T} }\mathbf {X} \right)^{-1}\mathbf {X} ^{\operatorname {T} }{\boldsymbol {\varepsilon }}.}$

Оценка

Предположим, b является значением «кандидата» для вектора параметров β . Величина y _i − x _i ^T b , называемая остатком для i -го наблюдения, измеряет вертикальное расстояние между точкой данных ( x _i , y _i ) и гиперплоскостью y = x ^T b и, таким образом, оценивает степень соответствие между фактическими данными и моделью. Сумма квадратов остатков ( SSR ) (также называемая суммой квадратов ошибок ( ESS ) или остаточной суммой квадратов ( RSS )) ^[3] является мерой общего соответствия модели:

${\displaystyle S(b)=\sum _{i=1}^{n}(y_{i}-x_{i}^{\operatorname {T} }b)^{2}=(y-Xb)^{\operatorname {T} }(y-Xb),}$

где T обозначает транспонирование матрицы , а строки X , обозначающие значения всех независимых переменных, связанных с конкретным значением зависимой переменной, равны X i ₌ x _i ^T. Значение b , которое минимизирует эту сумму, называется оценкой МНК для β . Функция S ( b ) квадратична по b с положительно определенным гессианом , и поэтому эта функция обладает единственным глобальным минимумом при , который может быть задан явной формулой: ^{[4] [доказательство]} ${\displaystyle b={\hat {\beta }}}$

${\displaystyle {\hat {\beta }}=\operatorname {argmin} _{b\in \mathbb {R} ^{p}}S(b)=(X^{\operatorname {T} }X)^{-1}X^{\operatorname {T} }y\ .}$

Произведение N = X ^T X является матрицей Грама , а его обратная матрица Q = N ^–1 является матрицей-кофактором β , [ ^{5] [6] [7]} тесно связанной с ее ковариационной матрицей C _β . Матрица ( X ^T X ) ^–1 X ^T = Q X ^T называется псевдообратной матрицей Мура–Пенроуза X. Эта формулировка подчеркивает тот факт, что оценка может быть выполнена тогда и только тогда, когда не существует идеальной мультиколлинеарности между объясняющие переменные (которые привели бы к тому, что матрица грамма не имела обратной).

После того, как мы оценили β , подобранные значения (или прогнозируемые значения ) из регрессии будут

${\displaystyle {\hat {y}}=X{\hat {\beta }}=Py,}$

где P = X ( X ^T X ) ⁻¹ X ^T — матрица проекции на пространство V , натянутое на столбцы X . Эту матрицу P также иногда называют шляпной матрицей , потому что она «надевает шляпу» на переменную y . Другая матрица, тесно связанная с P , — это матрица -аннулятор M = I _n − P ; это матрица проекции на пространство, ортогональное V . Обе матрицы P и M являются симметричными и идемпотентными (это означает, что P ² = P и M ² = M ) и относятся к матрице данных X через тождества PX = X и MX = 0 . ^[8] Матрица M создает остатки регрессии:

${\displaystyle {\hat {\varepsilon }}=y-{\hat {y}}=y-X{\hat {\beta }}=My=M(X\beta +\varepsilon )=(MX)\beta +M\varepsilon =M\varepsilon .}$

Используя эти остатки, мы можем оценить значение σ2 ^, используя приведенную статистику хи-квадрат :

${\displaystyle s^{2}={\frac {{\hat {\varepsilon }}^{\mathrm {T} }{\hat {\varepsilon }}}{n-p}}={\frac {(My)^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }M^{\mathrm {T} }My}{n-p}}={\frac {y^{\mathrm {T} }My}{n-p}}={\frac {S({\hat {\beta }})}{n-p}},\qquad {\hat {\sigma }}^{2}={\frac {n-p}{n}}\;s^{2}}$

Знаменатель n − p — это статистические степени свободы . Первая величина, s ² , является оценкой МНК для σ ² , тогда как вторая , является оценкой MLE для σ ² . Эти две оценки очень похожи в больших выборках; первая оценка всегда несмещена , тогда как вторая оценка смещена, но имеет меньшую среднеквадратическую ошибку . На практике чаще используется s ^{2 , поскольку он более удобен для проверки гипотез.} Квадратный корень из s ² называется стандартной ошибкой регрессии , ^[9] стандартной ошибкой регрессии , ^{[10] [11]} или стандартной ошибкой уравнения . ^[8] ${\displaystyle \scriptstyle {\hat {\sigma }}^{2}}$

Обычно степень соответствия регрессии МНК оценивают путем сравнения того, насколько первоначальная вариация в выборке может быть уменьшена путем регрессии на X. Коэффициент детерминации R ² определяется как отношение «объясненной» дисперсии к «общей» дисперсии зависимой переменной y в тех случаях, когда сумма квадратов регрессии равна сумме квадратов остатков: ^[12]

${\displaystyle R^{2}={\frac {\sum ({\hat {y}}_{i}-{\overline {y}})^{2}}{\sum (y_{i}-{\overline {y}})^{2}}}={\frac {y^{\mathrm {T} }P^{\mathrm {T} }LPy}{y^{\mathrm {T} }Ly}}=1-{\frac {y^{\mathrm {T} }My}{y^{\mathrm {T} }Ly}}=1-{\frac {\rm {RSS}}{\rm {TSS}}}}$

где TSS — общая сумма квадратов зависимой переменной, и — матрица единиц размера n × n . ( является центрирующей матрицей , которая эквивалентна регрессии по константе; она просто вычитает среднее значение из переменной.) Чтобы R ² имело смысл, матрица X данных о регрессорах должна содержать вектор-столбец из единиц, чтобы представить константа, коэффициент которой является точкой пересечения регрессии. В этом случае R ² всегда будет числом от 0 до 1, причем значения, близкие к 1, указывают на хорошую степень соответствия. ${\textstyle L=I_{n}-{\frac {1}{n}}J_{n}}$ ${\textstyle J_{n}}$ ${\displaystyle L}$

Дисперсия в предсказании независимой переменной как функции зависимой переменной приведена в статье Полиномиальные наименьшие квадраты .

Простая модель линейной регрессии

Если матрица данных X содержит только две переменные, константу и скалярный регрессор x _i , то это называется «простой моделью регрессии». Этот случай часто рассматривается на занятиях по статистике для начинающих, поскольку он дает гораздо более простые формулы, подходящие даже для ручного расчета. Параметры обычно обозначаются как ( α , β ) :

${\displaystyle y_{i}=\alpha +\beta x_{i}+\varepsilon _{i}.}$

Оценки методом наименьших квадратов в этом случае даются простыми формулами

${\displaystyle {\begin{aligned}{\widehat {\beta }}&={\frac {\sum _{i=1}^{n}{(x_{i}-{\bar {x}})(y_{i}-{\bar {y}})}}{\sum _{i=1}^{n}{(x_{i}-{\bar {x}})^{2}}}}\\[2pt]{\widehat {\alpha }}&={\bar {y}}-{\widehat {\beta }}\,{\bar {x}}\ ,\end{aligned}}}$

Альтернативные выводы

В предыдущем разделе оценка методом наименьших квадратов была получена как значение, которое минимизирует сумму квадратов остатков модели. Однако ту же оценку можно получить и из других подходов. Во всех случаях формула для оценки МНК остается той же: ^{^} β = ( X ^T X ) ⁻¹ X ^T y ; единственная разница заключается в том, как мы интерпретируем этот результат. ${\displaystyle {\hat {\beta }}}$

Проекция

Оценку OLS можно рассматривать как проекцию на линейное пространство, охватываемое регрессорами. (Здесь каждый из и относится к столбцу матрицы данных.) ${\displaystyle X_{1}}$ ${\displaystyle X_{2}}$

Для математиков МНК — это приближенное решение переопределенной системы линейных уравнений Xβ ≈ y , где β — неизвестное. Предполагая, что система не может быть решена точно (количество уравнений n намного больше числа неизвестных p ), мы ищем решение, которое могло бы обеспечить наименьшее расхождение между правой и левой частями. Другими словами, мы ищем решение, удовлетворяющее

${\displaystyle {\hat {\beta }}={\rm {arg}}\min _{\beta }\,\lVert \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}\rVert ,}$

где ‖ · ‖ — стандартная  норма L 2 в n -мерном евклидовом пространстве R ⁿ . Предсказанная величина Xβ представляет собой некую линейную комбинацию векторов регрессоров. Таким образом, вектор остатка y − Xβ будет иметь наименьшую длину, когда y проецируется ортогонально на линейное подпространство , натянутое столбцами X . Оценщик МНК в этом случае можно интерпретировать как коэффициенты векторного разложения ^{^} y = Py по базису X . ${\displaystyle {\hat {\beta }}}$

Другими словами, уравнения градиента в минимуме можно записать как:

${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})^{\top }\mathbf {X} =0.}$

Геометрическая интерпретация этих уравнений заключается в том , что вектор остатков ортогонален пространству столбцов X , поскольку скалярное произведение равно нулю для любого конформного вектора v . Это означает, что это самый короткий из всех возможных векторов , то есть дисперсия остатков минимально возможная. Это показано справа. ${\displaystyle \mathbf {y} -X{\hat {\boldsymbol {\beta }}}}$ ${\displaystyle (\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}})\cdot \mathbf {X} \mathbf {v} }$ ${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\hat {\beta }}}}$ ${\displaystyle \mathbf {y} -\mathbf {X} {\boldsymbol {\beta }}}$

Вводя матрицу K в предположении, что матрица неособа и K ^T X = 0 (см. Ортогональные проекции ), вектор невязки должен удовлетворять следующему уравнению: ${\displaystyle {\hat {\boldsymbol {\gamma }}}}$ ${\displaystyle [\mathbf {X} \ \mathbf {K} ]}$

${\displaystyle {\hat {\mathbf {r} }}:=\mathbf {y} -\mathbf {X} {\hat {\boldsymbol {\beta }}}=\mathbf {K} {\hat {\boldsymbol {\gamma }}}.}$

Таким образом, уравнение и решение линейного метода наименьших квадратов описываются следующим образом:

${\displaystyle {\begin{aligned}\mathbf {y} &={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}{\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}},\\{}\Rightarrow {\begin{bmatrix}{\hat {\boldsymbol {\beta }}}\\{\hat {\boldsymbol {\gamma }}}\end{bmatrix}}&={\begin{bmatrix}\mathbf {X} &\mathbf {K} \end{bmatrix}}^{-1}\mathbf {y} ={\begin{bmatrix}\left(\mathbf {X} ^{\top }\mathbf {X} \right)^{-1}\mathbf {X} ^{\top }\\\left(\mathbf {K} ^{\top }\mathbf {K} \right)^{-1}\mathbf {K} ^{\top }\end{bmatrix}}\mathbf {y} .\end{aligned}}}$

Другой способ взглянуть на это — рассматривать линию регрессии как средневзвешенное значение линий, проходящих через комбинацию любых двух точек в наборе данных. ^[13] Хотя этот способ расчета требует больше вычислительных затрат, он обеспечивает лучшую интуицию при использовании МНК.

Максимальная вероятность

Средство оценки OLS идентично средству оценки максимального правдоподобия (MLE) при условии нормальности ошибок. ^{[14] [доказательство]} Это предположение о нормальности имеет историческое значение, поскольку оно послужило основой для ранних работ Юла и Пирсона по линейному регрессионному анализу . ^{[ нужна цитата ]} Из свойств MLE мы можем сделать вывод, что оценка OLS асимптотически эффективна (в смысле достижения границы Крамера-Рао для дисперсии), если выполняется предположение о нормальности. ^[15]

Обобщенный метод моментов

В iid случае оценку МНК также можно рассматривать как оценку GMM , возникающую из моментных условий

${\displaystyle \mathrm {E} {\big [}\,x_{i}\left(y_{i}-x_{i}^{\operatorname {T} }\beta \right)\,{\big ]}=0.}$

Эти моментные условия гласят, что регрессоры не должны быть коррелированы с ошибками. Поскольку x _i является p -вектором, количество моментных условий равно размерности вектора параметров β и, таким образом, система точно идентифицируется. Это так называемый классический случай GMM, когда оценка не зависит от выбора весовой матрицы.

Обратите внимание, что исходное предположение о строгой экзогенности E[ ε _i  | x _i ] = 0 подразумевает гораздо более богатый набор моментных условий, чем указано выше. В частности, из этого предположения следует, что для любой вектор-функции ƒ будет выполняться моментное условие E[ ƒ ( x _i ) · ε _i ] = 0 . Однако с помощью теоремы Гаусса-Маркова можно показать , что оптимальный выбор функции ƒ состоит в том, чтобы взять ƒ ( x ) = x , что приводит к уравнению момента, опубликованному выше.

Характеристики

Предположения

Существует несколько различных схем, в которых можно использовать модель линейной регрессии , чтобы сделать применимым метод МНК. Каждая из этих настроек дает одни и те же формулы и одинаковые результаты. Единственная разница заключается в интерпретации и предположениях, которые необходимо сделать, чтобы метод дал значимые результаты. Выбор применимой структуры зависит главным образом от характера имеющихся данных и от задачи вывода, которую необходимо выполнить.

Одно из различий в интерпретации заключается в том, следует ли рассматривать регрессоры как случайные переменные или как заранее определенные константы. В первом случае ( случайный план ) регрессоры xi являются случайными и выбираются вместе с _yi из некоторой _{совокупности} , как в обсервационном исследовании . Такой подход позволяет более естественно изучать асимптотические свойства оценок. В другой интерпретации ( фиксированный план ) регрессоры X рассматриваются как известные константы, заданные планом , а выборка y производится условно по значениям X , как в эксперименте . Для практических целей это различие часто не имеет значения, поскольку оценка и вывод выполняются с учетом X. Все результаты, изложенные в этой статье, находятся в рамках метода случайного планирования.

Классическая модель линейной регрессии

Классическая модель фокусируется на оценке и выводе «конечной выборки», что означает, что количество наблюдений n фиксировано. Это контрастирует с другими подходами, изучающими асимптотическое поведение МНК и изучающими поведение при большом количестве выборок.

• Правильная спецификация . Линейная функциональная форма должна совпадать с формой реального процесса генерации данных.
• Строгая экзогенность . Ошибки в регрессии должны иметь условный средний ноль: ^[16]
  $${\displaystyle \operatorname {E} [\,\varepsilon \mid X\,]=0.}$$
  Непосредственным следствием предположения экзогенности является то, что среднее значение ошибок равно нулю: E[ ε ] = 0 (для закона полного ожидания ), и что регрессоры не коррелируют с ошибками: E[ X ^Tε ] = 0 .
  Предположение экзогенности имеет решающее значение для теории МНК. Если это справедливо, то переменные регрессора называются экзогенными . Если это не так, то те регрессоры, которые коррелируют с членом ошибки, называются эндогенными ^[17] , и оценка OLS становится смещенной. В этом случае для вывода можно использовать метод инструментальных переменных .
• Никакой линейной зависимости . Все регрессоры в X должны быть линейно независимыми . Математически это означает, что матрица X почти наверняка должна иметь полный ранг столбца : ^[18]
  $${\displaystyle \Pr \!{\big [}\,\operatorname {rank} (X)=p\,{\big ]}=1.}$$
  Обычно также предполагается, что регрессоры имеют конечные моменты, по крайней мере, до второго момента. Тогда матрица Q _xx = E[ X ^T X  /  n ] конечна и положительно полуопределена.
  Когда это предположение нарушается, регрессоры называются линейно зависимыми или совершенно мультиколлинеарными . В таком случае значение коэффициента регрессии β узнать невозможно, хотя предсказание значений y все еще возможно для новых значений регрессоров, лежащих в том же линейно зависимом подпространстве.
• Сферические ошибки : ^[18]
  $${\displaystyle \operatorname {Var} [\,\varepsilon \mid X\,]=\sigma ^{2}I_{n},}$$
  где I _n — единичная матрица в размерности n , а σ ² — параметр, который определяет дисперсию каждого наблюдения. Этот σ ² считается в модели мешающим параметром , хотя обычно он также оценивается. Если это предположение нарушается, то оценки МНК все еще действительны, но уже не эффективны.
  Это предположение принято разбивать на две части:
  • Гомоскедастичность : E[  ε _я ²  | X  ] = σ ² , что означает, что член ошибки имеет одинаковую дисперсию σ ² в каждом наблюдении. Когда это требование нарушается, это называется гетероскедастичностью . В таком случае более эффективной оценкой будет метод взвешенных наименьших квадратов . Если ошибки имеют бесконечную дисперсию, то оценки МНК также будут иметь бесконечную дисперсию (хотя по закону больших чисел они, тем не менее, будут стремиться к истинным значениям, пока ошибки имеют нулевое среднее). В этом случаерекомендуется использовать надежные методы оценки .
  • Нет автокорреляции : ошибки не коррелируют между наблюдениями: E[  ε _i ε _j  | Икс  ] знак равно 0 для я ≠ j . Это предположение может быть нарушено в контексте данных временных рядов , панельных данных , кластерных выборок, иерархических данных, данных повторных измерений, продольных данных и других данных с зависимостями. В таких случаях обобщенный метод наименьших квадратов обеспечивает лучшую альтернативу, чем МНК. Другое выражение автокорреляции — серийная корреляция .
• Нормальность . Иногда дополнительно предполагается, что ошибки имеют нормальное распределение , обусловленное регрессорами: ^[19]
  $${\displaystyle \varepsilon \mid X\sim {\mathcal {N}}(0,\sigma ^{2}I_{n}).}$$
  Это предположение не является необходимым для достоверности метода МНК, хотя некоторые дополнительные свойства конечной выборки могут быть установлены в случае, когда это необходимо (особенно в области проверки гипотез). Кроме того, когда ошибки являются нормальными, оценка OLS эквивалентна оценке максимального правдоподобия (MLE) и, следовательно, асимптотически эффективна в классе всех регулярных оценок . Важно отметить, что предположение о нормальности применимо только к погрешностям; Вопреки распространенному заблуждению, ответная (зависимая) переменная не обязательно должна иметь нормальное распределение. ^[20]

Независимые и одинаково распределенные (iid)

В некоторых приложениях, особенно с данными поперечного сечения , налагается дополнительное предположение — что все наблюдения независимы и одинаково распределены. Это означает, что все наблюдения берутся из случайной выборки , что упрощает и облегчает интерпретацию всех перечисленных ранее предположений. Также эта структура позволяет формулировать асимптотические результаты (например, размер выборки n  → ∞ ), которые понимаются как теоретическая возможность получения новых независимых наблюдений из процесса генерации данных . Список предположений в этом случае следующий:

• наблюдения iid : ( x _i , y _i ) не зависит от и имеет то же распределение , что и ( x _j , y _j ) для всех i ≠ j ;
• нет совершенной мультиколлинеарности : Q _xx = E[  x _i  x _i ^T  ] — положительно определенная матрица ;
• экзогенность : E[  ε _я  | х _я  ] = 0;
• гомоскедастичность : Var[  ε _я  | Икс _я  ] знак равно σ ² .

Модель временных рядов

• Случайный процесс { xi _, yi } стационарен и эргодичен ; _{_} _ если { x _i , y _i } нестационарно, результаты МНК часто оказываются ложными, если только { x _i , y _i } не является коинтегрирующим . ^[21]
• Регрессоры заранее определены : E[ x _i ε _i ] = 0 для всех i = 1, ..., n ;
• Матрица p × p Q _xx = E[  x _i  x _i ^T  ] имеет полный ранг и, следовательно , положительно определена ;
• { x _я ε _я } -- мартингальная разностная последовательность с конечной матрицей вторых моментов Q _{xxε ²} знак равно E[  ε _я ² x _я  x _я ^T  ] .

Конечные свойства выборки

Прежде всего, при строгом предположении экзогенности оценки МНК и s ² являются несмещенными , что означает, что их ожидаемые значения совпадают с истинными значениями параметров: ^{[22] [доказательство]} ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {E} [\,{\hat {\beta }}\mid X\,]=\beta ,\quad \operatorname {E} [\,s^{2}\mid X\,]=\sigma ^{2}.}$

Если строгая экзогенность не соблюдается (как в случае со многими моделями временных рядов , где экзогенность предполагается только в отношении прошлых потрясений, но не будущих), то эти оценки будут смещены в конечных выборках.

Дисперсионно -ковариационная матрица (или просто ковариационная матрица ) равна ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\hat {\beta }}\mid X\,]=\sigma ^{2}\left(X^{\operatorname {T} }X\right)^{-1}=\sigma ^{2}Q.}$

В частности, стандартная ошибка каждого коэффициента равна квадратному корню из j -го диагонального элемента этой матрицы. ^{Оценка этой стандартной ошибки} получается заменой неизвестной величины σ2 на ее ^оценку s2 . Таким образом, ${\displaystyle \scriptstyle {\hat {\beta }}_{j}}$

${\displaystyle {\widehat {\operatorname {s.\!e.} }}({\hat {\beta }}_{j})={\sqrt {s^{2}\left(X^{\operatorname {T} }X\right)_{jj}^{-1}}}}$

Также можно легко показать, что оценка не коррелирует с остатками модели: ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle \operatorname {Cov} [\,{\hat {\beta }},{\hat {\varepsilon }}\mid X\,]=0.}$

Теорема Гаусса -Маркова утверждает, что при допущении сферических ошибок (т. е. ошибки должны быть некоррелированными и гомоскедастическими ) оценка эффективна в классе линейных несмещенных оценок. Это называется лучшей линейной несмещенной оценкой (СИНИЙ). Эффективность следует понимать так, как если бы мы хотели найти какую-то другую оценку , которая была бы линейной по y и несмещенной, тогда ^[23] ${\displaystyle \scriptstyle {\hat {\beta }}}$ ${\displaystyle \scriptstyle {\tilde {\beta }}}$

${\displaystyle \operatorname {Var} [\,{\tilde {\beta }}\mid X\,]-\operatorname {Var} [\,{\hat {\beta }}\mid X\,]\geq 0}$

в том смысле, что это неотрицательно-определенная матрица . Эта теорема устанавливает оптимальность только в классе линейных несмещенных оценок, что весьма ограничительно. В зависимости от распределения ошибок ε другие нелинейные средства оценки могут давать лучшие результаты, чем OLS.

Предполагая нормальность

Все перечисленные выше свойства действительны независимо от основного распределения условий ошибки. Однако если вы готовы предположить, что предположение о нормальности выполнено (то есть, что ε ~ N (0, σ ² I _n ) ), то можно указать дополнительные свойства оценок МНК.

Оценка имеет нормальное распределение со средним значением и дисперсией, указанными ранее: ^[24] ${\displaystyle \scriptstyle {\hat {\beta }}}$

${\displaystyle {\hat {\beta }}\ \sim \ {\mathcal {N}}{\big (}\beta ,\ \sigma ^{2}(X^{\mathrm {T} }X)^{-1}{\big )}.}$

Эта оценка достигает границы Крамера – Рао для модели и, таким образом, является оптимальной в классе всех несмещенных оценок. ^[15] Обратите внимание, что в отличие от теоремы Гаусса–Маркова этот результат устанавливает оптимальность как среди линейных, так и среди нелинейных оценок, но только в случае нормально распределенных членов ошибок.

Оценка s ² будет пропорциональна распределению хи-квадрат : ^[25]

${\displaystyle s^{2}\ \sim \ {\frac {\sigma ^{2}}{n-p}}\cdot \chi _{n-p}^{2}}$

Дисперсия этой оценки равна 2 σ ⁴ /( n  −  p ) , что не достигает границы Крамера – Рао для 2 σ ⁴ / n . Однако было показано, что не существует несмещенных оценок σ ² с дисперсией меньшей, чем у оценки s ² . ^[26] Если мы готовы разрешить использование смещенных оценок и рассмотреть класс оценок, которые пропорциональны сумме квадратов остатков (SSR) модели, то лучшая (в смысле среднеквадратичной ошибки ) оценка в этой класс будет ^~ σ ² = SSR  /  ( n  −  p  + 2) , что даже превосходит границу Крамера – Рао в случае, когда существует только один регрессор ( p = 1 ). ^[27]

Более того , оценки и s ² независимы , ^[28] этот факт полезен при построении t- и F-тестов для регрессии. ${\displaystyle \scriptstyle {\hat {\beta }}}$

Влиятельные наблюдения

Как упоминалось ранее, оценщик является линейным по y , что означает, что он представляет собой линейную комбинацию зависимых переменных y _i . Веса в этой линейной комбинации являются функциями регрессоров X и обычно неравны. Наблюдения с высокими весами называются влиятельными , поскольку они оказывают более выраженное влияние на значение оценки. ${\displaystyle {\hat {\beta }}}$

Чтобы проанализировать, какие наблюдения оказывают влияние, мы удаляем конкретное j -е наблюдение и рассматриваем, насколько изменятся оцененные величины (аналогично методу складного ножа ). Можно показать, что изменение оценки МНК для β будет равно ^[29]

${\displaystyle {\hat {\beta }}^{(j)}-{\hat {\beta }}=-{\frac {1}{1-h_{j}}}(X^{\mathrm {T} }X)^{-1}x_{j}^{\mathrm {T} }{\hat {\varepsilon }}_{j}\,,}$

где h _j = x _j ^T  ( X ^T X ) ⁻¹ x _j — j -й диагональный элемент матрицы шляпки P , а x _j — вектор регрессоров, соответствующий j -му наблюдению. Аналогично, изменение прогнозируемого значения для j -го наблюдения в результате исключения этого наблюдения из набора данных будет равно ^[29]

${\displaystyle {\hat {y}}_{j}^{(j)}-{\hat {y}}_{j}=x_{j}^{\mathrm {T} }{\hat {\beta }}^{(j)}-x_{j}^{\operatorname {T} }{\hat {\beta }}=-{\frac {h_{j}}{1-h_{j}}}\,{\hat {\varepsilon }}_{j}}$

Судя по свойствам матрицы шляпы, 0 ≤ h _j ≤ 1 , и они суммируются до p , так что в среднем h _j ≈ p/n . Эти величины h _j называются рычагами , а наблюдения с высокими h _j называются точками рычага . ^[30] Обычно наблюдения с высоким уровнем рычагов следует проверять более тщательно на случай, если они ошибочны, являются выбросами или каким-либо другим образом нетипичны для остального набора данных.

Разделенная регрессия

Иногда переменные и соответствующие параметры регрессии можно логически разделить на две группы, чтобы регрессия приняла форму

${\displaystyle y=X_{1}\beta _{1}+X_{2}\beta _{2}+\varepsilon ,}$

где X ₁ и X ₂ имеют размеры n × p ₁ , n × p ₂ , а β ₁ , β ₂ представляют собой векторы p ₁ × 1 и p ₂ × 1, причем p ₁ + p ₂ = p .

Теорема Фриша -Во-Ловелла утверждает, что в этой регрессии остатки и оценка МНК будут численно идентичны остаткам и оценке МНК для β ₂ в следующей регрессии: ^[31] ${\displaystyle {\hat {\varepsilon }}}$ ${\displaystyle \scriptstyle {\hat {\beta }}_{2}}$

${\displaystyle M_{1}y=M_{1}X_{2}\beta _{2}+\eta \,,}$

где M ₁ — матрица аннулятора для регрессоров X ₁ .

Теорема может быть использована для установления ряда теоретических результатов. Например, наличие регрессии с константой и другим регрессором эквивалентно вычитанию средних значений из зависимой переменной и регрессора, а затем запуску регрессии для переменных с пониженным значением, но без постоянного члена.

Ограниченная оценка

Предположим, известно, что коэффициенты регрессии удовлетворяют системе линейных уравнений

${\displaystyle A\colon \quad Q^{\operatorname {T} }\beta =c,\,}$

где Q — матрица p × q полного ранга, а c — вектор известных констант q × 1, где q < p . В этом случае оценка методом наименьших квадратов эквивалентна минимизации суммы квадратов остатков модели с учетом ограничения A. Оценка методом наименьших квадратов с ограничениями (CLS) может быть задана явной формулой: ^[32]

${\displaystyle {\hat {\beta }}^{c}={\hat {\beta }}-(X^{\operatorname {T} }X)^{-1}Q{\Big (}Q^{\operatorname {T} }(X^{\operatorname {T} }X)^{-1}Q{\Big )}^{-1}(Q^{\operatorname {T} }{\hat {\beta }}-c).}$

Это выражение для оценки с ограничениями справедливо до тех пор, пока матрица X ^T X обратима. В начале статьи предполагалось, что эта матрица имеет полный ранг, и было отмечено, что при невыполнении условия ранга β не будет идентифицируемой. Однако может случиться так, что добавление ограничения A сделает β идентифицируемым, и в этом случае хотелось бы найти формулу для оценки. Оценка равна ^[33]

${\displaystyle {\hat {\beta }}^{c}=R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }y+{\Big (}I_{p}-R(R^{\operatorname {T} }X^{\operatorname {T} }XR)^{-1}R^{\operatorname {T} }X^{\operatorname {T} }X{\Big )}Q(Q^{\operatorname {T} }Q)^{-1}c,}$

где R — матрица размера p ×( p  −  q ) такая, что матрица [ QR ] невырождена, и R ^T Q = 0 . Такую матрицу всегда можно найти, хотя, как правило, она не единственна. Вторая формула совпадает с первой в случае, когда X ^T X обратима. ^[33]

Большой образец недвижимости

Оценщики методом наименьших квадратов представляют собой точечные оценки параметров модели линейной регрессии β . Однако, как правило, мы также хотим знать, насколько близки эти оценки к истинным значениям параметров. Другими словами, мы хотим построить интервальные оценки .

Поскольку мы не сделали никаких предположений о распределении ошибки ε _i , невозможно вывести распределение оценок и . Тем не менее, мы можем применить центральную предельную теорему , чтобы получить их асимптотические свойства, когда размер выборки n стремится к бесконечности. Хотя размер выборки обязательно конечен, принято предполагать, что n «достаточно велико», так что истинное распределение оценки OLS близко к своему асимптотическому пределу. ${\displaystyle {\hat {\beta }}}$ ${\displaystyle {\hat {\sigma }}^{2}}$

Мы можем показать, что при предположениях модели оценка наименьших квадратов для β непротиворечива (то есть сходится по вероятности к β ) и асимптотически нормальна: ^{[доказательство]} ${\displaystyle {\hat {\beta }}}$

${\displaystyle ({\hat {\beta }}-\beta )\ {\xrightarrow {d}}\ {\mathcal {N}}{\big (}0,\;\sigma ^{2}Q_{xx}^{-1}{\big )},}$

где ${\displaystyle Q_{xx}=X^{\operatorname {T} }X.}$

Интервалы

Используя это асимптотическое распределение, можно построить приближенные двусторонние доверительные интервалы для j -го компонента вектора как ${\displaystyle {\hat {\beta }}}$

${\displaystyle \beta _{j}\in {\bigg [}\ {\hat {\beta }}_{j}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}}}\ {\bigg ]}}$   на уровне достоверности 1 -  α ,

где q обозначает функцию квантиля стандартного нормального распределения, а [·] _jj — j -й диагональный элемент матрицы.

Аналогично, оценка методом наименьших квадратов для σ ² также непротиворечива и асимптотически нормальна (при условии, что существует четвертый момент ε _i ) с предельным распределением

${\displaystyle ({\hat {\sigma }}^{2}-\sigma ^{2})\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\operatorname {E} \left[\varepsilon _{i}^{4}\right]-\sigma ^{4}\right).}$

Эти асимптотические распределения можно использовать для прогнозирования, проверки гипотез, построения других оценок и т. д. В качестве примера рассмотрим задачу прогнозирования. Предположим , что это некоторая точка в области распределения регрессоров, и нужно знать, какой была бы переменная отклика в этой точке. Средний ответ – это количество , тогда как прогнозируемый ответ – это . Очевидно, что прогнозируемый ответ является случайной величиной, его распределение можно получить из : ${\displaystyle x_{0}}$ ${\displaystyle y_{0}=x_{0}^{\mathrm {T} }\beta }$ ${\displaystyle {\hat {y}}_{0}=x_{0}^{\mathrm {T} }{\hat {\beta }}}$ ${\displaystyle {\hat {\beta }}}$

${\displaystyle \left({\hat {y}}_{0}-y_{0}\right)\ {\xrightarrow {d}}\ {\mathcal {N}}\left(0,\;\sigma ^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}\right),}$

что позволяет построить доверительные интервалы для построения среднего ответа: ${\displaystyle y_{0}}$

${\displaystyle y_{0}\in \left[\ x_{0}^{\mathrm {T} }{\hat {\beta }}\pm q_{1-{\frac {\alpha }{2}}}^{{\mathcal {N}}(0,1)}\!{\sqrt {{\hat {\sigma }}^{2}x_{0}^{\mathrm {T} }Q_{xx}^{-1}x_{0}}}\ \right]}$   на уровне достоверности 1-  α .

Проверка гипотезы

Особенно широко используются два теста гипотез. Во-первых, нужно знать, является ли предполагаемое уравнение регрессии чем-то лучше, чем простое предсказание того, что все значения переменной отклика равны ее выборочному среднему (если нет, то говорят, что оно не имеет объяснительной силы). Нулевая гипотеза об отсутствии объяснительной ценности оцененной регрессии проверяется с помощью F-теста . Если вычисленное значение F оказывается достаточно большим, чтобы превысить его критическое значение для заранее выбранного уровня значимости, нулевая гипотеза отклоняется и принимается альтернативная гипотеза о том, что регрессия имеет объяснительную силу. В противном случае принимается нулевая гипотеза об отсутствии объяснительной силы.

Во-вторых, для каждой интересующей объясняющей переменной нужно знать, значительно ли ее расчетный коэффициент отличается от нуля, то есть действительно ли эта конкретная объясняющая переменная обладает объяснительной силой в предсказании переменной отклика. Здесь нулевая гипотеза состоит в том, что истинный коэффициент равен нулю. Эта гипотеза проверяется путем вычисления t-статистики коэффициента как отношения оценки коэффициента к его стандартной ошибке . Если t-статистика больше заранее определенного значения, нулевая гипотеза отклоняется и обнаруживается, что переменная имеет объяснительную силу, а ее коэффициент значительно отличается от нуля. В противном случае принимается нулевая гипотеза о нулевом значении истинного коэффициента.

Кроме того, тест Чоу используется для проверки того, имеют ли две подвыборки одинаковые значения истинного коэффициента. Сумма квадратов остатков регрессий в каждом из подмножеств и в объединенном наборе данных сравнивается путем вычисления F-статистики; если оно превышает критическое значение, нулевая гипотеза об отсутствии различий между двумя подмножествами отклоняется; в противном случае оно принимается.

Пример с реальными данными

В следующем наборе данных указаны средние показатели роста и веса американских женщин в возрасте 30–39 лет (источник: Всемирный альманах и Книга фактов, 1975 ).

Когда моделируется только одна зависимая переменная, диаграмма рассеяния покажет форму и силу связи между зависимой переменной и регрессорами. Это также может выявить выбросы, гетероскедастичность и другие аспекты данных, которые могут усложнить интерпретацию подобранной регрессионной модели. Диаграмма рассеяния показывает, что связь сильная и может быть аппроксимирована квадратичной функцией. OLS может обрабатывать нелинейные отношения, вводя регрессор HEIGHT ² . Затем регрессионная модель становится множественной линейной моделью:

${\displaystyle w_{i}=\beta _{1}+\beta _{2}h_{i}+\beta _{3}h_{i}^{2}+\varepsilon _{i}.}$

Подстроенная регрессия

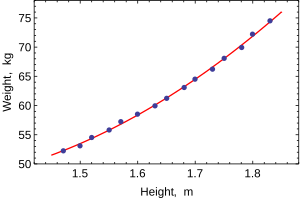
Вывод большинства популярных статистических пакетов будет выглядеть примерно так:

В этой таблице:

• В столбце « Значение» приведены оценки параметров β _j по методу наименьших квадратов.
• В столбце «Стандартная ошибка» показаны стандартные ошибки оценки каждого коэффициента: ${\displaystyle {\hat {\sigma }}_{j}=\left({\hat {\sigma }}^{2}\left[Q_{xx}^{-1}\right]_{jj}\right)^{\frac {1}{2}}}$
• Столбцы t-статистики и p-значения проверяют, может ли какой-либо из коэффициентов быть равен нулю. t - статистика рассчитывается просто как . Если ошибки ε подчиняются нормальному распределению, t соответствует распределению Стьюдента. При более слабых условиях t асимптотически нормально. Большие значения t указывают на то, что нулевую гипотезу можно отвергнуть и что соответствующий коэффициент не равен нулю. Второй столбец, p -value , выражает результаты проверки гипотезы как уровень значимости . Обычно значения p меньше 0,05 считаются свидетельством того, что коэффициент численности населения не равен нулю. ${\displaystyle t={\hat {\beta }}_{j}/{\hat {\sigma }}_{j}}$
• R-квадрат — это коэффициент детерминации , указывающий на степень соответствия регрессии. Эта статистика будет равна единице, если соответствие идеальное, и нулю, когда регрессоры X не имеют никакой объяснительной силы. Это смещенная оценка генерального R-квадрата , и она никогда не уменьшится, если будут добавлены дополнительные регрессоры, даже если они не имеют значения.
• Скорректированный R-квадрат — это слегка модифицированная версия , предназначенная для наказания за избыточное количество регрессоров, которые не увеличивают объяснительную силу регрессии. Эта статистика всегда меньше , может уменьшаться по мере добавления новых регрессоров и даже быть отрицательной для плохо подходящих моделей: ${\displaystyle R^{2}}$ ${\displaystyle R^{2}}$

${\displaystyle {\overline {R}}^{2}=1-{\frac {n-1}{n-p}}(1-R^{2})}$

• Логарифмическое правдоподобие рассчитывается в предположении, что ошибки подчиняются нормальному распределению. Несмотря на то, что это предположение не очень разумно, эта статистика все же может найти применение при проведении LR-тестов.
• Статистика Дурбина-Ватсона проверяет, существуют ли какие-либо доказательства серийной корреляции между остатками. Как правило, значение меньше 2 будет свидетельствовать о положительной корреляции.
• Информационный критерий Акаике и критерий Шварца используются для выбора модели. Обычно при сравнении двух альтернативных моделей меньшие значения одного из этих критериев указывают на лучшую модель. ^[34]
• Стандартная ошибка регрессии — это оценка σ , стандартной ошибки термина ошибки.
• Общая сумма квадратов , модельная сумма квадратов и остаточная сумма квадратов говорят нам, какая часть исходных изменений в выборке была объяснена регрессией.
• F-статистика пытается проверить гипотезу о том, что все коэффициенты (кроме точки пересечения) равны нулю. Эта статистика имеет распределение F ( p – 1 , n – p ) при нулевой гипотезе и предположении нормальности, а ее значение p указывает на вероятность того, что гипотеза действительно верна. Обратите внимание: если ошибки не являются нормальными, эта статистика становится недействительной, и следует использовать другие тесты, такие как тест Вальда или тест LR .

График остатков

Обычный анализ методом наименьших квадратов часто включает использование диагностических графиков, предназначенных для обнаружения отклонений данных от предполагаемой формы модели. Вот некоторые из распространенных диагностических графиков:

• Остатки от объясняющих переменных в модели. Нелинейная связь между этими переменными предполагает, что линейность условной средней функции может не соблюдаться. Различные уровни изменчивости остатков для разных уровней объясняющих переменных позволяют предположить возможную гетероскедастичность.
• Остатки от объясняющих переменных, которых нет в модели. Любая связь остатков с этими переменными предполагает рассмотрение этих переменных для включения в модель.
• Остатки против подобранных значений, . ${\displaystyle {\hat {y}}}$
• Остатки против предыдущего остатка. Этот график может выявить серийные корреляции в остатках.

Важным фактором при выполнении статистических выводов с использованием регрессионных моделей является способ выборки данных. В этом примере данные представляют собой средние значения, а не измерения по отдельным женщинам. Подгонка модели очень хорошая, но это не означает, что вес отдельной женщины можно с высокой точностью предсказать, основываясь только на ее росте.

Чувствительность к округлению

Этот пример также демонстрирует, что коэффициенты, определенные в результате этих расчетов, чувствительны к тому, как подготавливаются данные. Первоначально высоты были округлены до ближайшего дюйма, а затем были преобразованы и округлены до ближайшего сантиметра. Поскольку коэффициент преобразования составляет один дюйм в 2,54 см, это не точное преобразование. Исходные дюймы можно восстановить с помощью Round(x/0,0254), а затем повторно преобразовать в метрические без округления. Если это сделать, результаты будут такими:

Остатки квадратичной аппроксимации для правильно и неправильно преобразованных данных.

Использование любого из этих уравнений для прогнозирования веса женщины ростом 5 футов 6 дюймов (1,6764 м) дает аналогичные значения: 62,94 кг с округлением против 62,98 кг без округления. Таким образом, кажущееся небольшим изменение данных оказывает реальное влияние на коэффициенты. но небольшое влияние на результаты уравнения.

Хотя это может выглядеть безобидным в середине диапазона данных, оно может стать значимым в крайних точках или в случае, когда подобранная модель используется для проецирования за пределы диапазона данных ( экстраполяция ).

Это подчеркивает распространенную ошибку: этот пример является злоупотреблением МНК, который по своей сути требует, чтобы ошибки в независимой переменной (в данном случае высоте) были нулевыми или, по крайней мере, незначительными. Первоначальное округление до ближайшего дюйма плюс любые фактические ошибки измерения составляют конечную и существенную ошибку. В результате подобранные параметры не являются лучшими оценками, какими они предположительно являются. Хотя это и не совсем ложно, ошибка в оценке будет зависеть от относительного размера ошибок x и y .

Еще один пример с менее реальными данными

Постановка задачи

Мы можем использовать механизм наименьших квадратов, чтобы вычислить уравнение орбиты двух тел в полярных базовых координатах. Обычно используется уравнение: где находится радиус расстояния объекта от одного из тел. В уравнении параметры и используются для определения траектории орбиты. Мы измерили следующие данные. ${\displaystyle r(\theta )={\frac {p}{1-e\cos(\theta )}}}$ ${\displaystyle r(\theta )}$ ${\displaystyle p}$ ${\displaystyle e}$

Нам нужно найти аппроксимацию методом наименьших квадратов и для данных данных. ${\displaystyle e}$ ${\displaystyle p}$

Решение

Сначала нам нужно представить e и p в линейной форме. Итак, мы собираемся переписать уравнение как . Кроме того, можно было бы использовать апсиды , расширив их дополнительным параметром , который является линейным как по отношению, так и по дополнительной базисной функции , используемой для extra . Мы используем исходную двухпараметрическую форму для представления наших данных наблюдений как: ${\displaystyle r(\theta )}$ ${\displaystyle {\frac {1}{r(\theta )}}={\frac {1}{p}}-{\frac {e}{p}}\cos(\theta )}$ ${\displaystyle \cos(\theta )}$ ${\displaystyle \cos(\theta -\theta _{0})=\cos(\theta )\cos(\theta _{0})+\sin(\theta )\sin(\theta _{0})}$ ${\displaystyle \cos(\theta )}$ ${\displaystyle \sin(\theta )}$ ${\displaystyle \tan \theta _{0}=\sin(\theta _{0})/\cos(\theta _{0})}$

${\displaystyle A^{T}A{\binom {x}{y}}=A^{T}b}$где is и is и построено так, что первый столбец представляет собой коэффициент , а второй столбец представляет собой коэффициент и представляет собой значения для соответствующих so и ${\displaystyle x}$ ${\displaystyle {\frac {1}{p}}}$ ${\displaystyle y}$ ${\displaystyle {\frac {e}{p}}}$ ${\displaystyle A}$ ${\displaystyle {\frac {1}{p}}}$ ${\displaystyle {\frac {e}{p}}}$ ${\displaystyle b}$ ${\displaystyle {\frac {1}{r(\theta )}}}$ ${\displaystyle A={\begin{bmatrix}1&-0.731354\\1&-0.707107\\1&-0.615661\\1&\ 0.052336\\1&0.309017\\1&0.438371\end{bmatrix}}}$ ${\displaystyle b={\begin{bmatrix}0.21220\\0.21958\\0.24741\\0.45071\\0.52883\\0.56820\end{bmatrix}}.}$

Решив, получим ${\displaystyle {\binom {x}{y}}={\binom {0.43478}{0.30435}}}$

так и ${\displaystyle p={\frac {1}{x}}=2.3000}$ ${\displaystyle e=p\cdot y=0.70001}$

Смотрите также

• Байесовский метод наименьших квадратов
• Регрессия Фамы – Макбета
• Нелинейный метод наименьших квадратов
• Численные методы линейного метода наименьших квадратов
• Идентификация нелинейной системы

Рекомендации

1. «Каков полный список обычных предположений для линейной регрессии?» Крест проверен . Проверено 28 сентября 2022 г.
2. Голдбергер, Артур С. (1964). «Классическая линейная регрессия». Эконометрическая теория. Нью-Йорк: Джон Уайли и сыновья. стр. 158. ISBN 0-471-31101-4.
3. Хаяси, Фумио (2000). Эконометрика . Издательство Принстонского университета. п. 15.
4. Хаяши (2000, стр. 18)
5. Гилани, Чарльз Д.; Пол Р. Вольф, доктор философии (12 июня 2006 г.). Корректирующие расчеты: пространственный анализ данных. ISBN 9780471697282.
6. Хофманн-Велленхоф, Бернхард; Лихтенеггер, Герберт; Васле, Эльмар (20 ноября 2007 г.). GNSS – глобальные навигационные спутниковые системы: GPS, ГЛОНАСС, Galileo и другие. ISBN 9783211730171.
7. Сюй, Гочан (5 октября 2007 г.). GPS: теория, алгоритмы и приложения. ISBN 9783540727156.
8. Хаяши (2000, стр. 19)
9. Джулиан Фарауэй (2000), Практическая регрессия и Anova с использованием R
10. Кенни, Дж.; Хранение, Е.С. (1963). Математика статистики . ван Ностранд. п. 187.
11. Цвиллингер, Д. (1995). Стандартные математические таблицы и формулы . Чепмен и Холл/CRC. п. 626. ИСБН 0-8493-2479-3.
12. Хаяси (2000, стр. 20)
13. Акбарзаде, Вахаб (7 мая 2014 г.). «Оценка линии».
14. Хаяси (2000, стр. 49)
15. Хаяши (2000, стр. 52)
16. Хаяши (2000, стр. 7)
17. Хаяши (2000, стр. 187)
18. Хаяши (2000, стр. 10)
19. Хаяси (2000, стр. 34)
20. Уильямс, Миннесота; Грахалес, Калифорния; Куркевич, Д (2013). «Предположения о множественной регрессии: исправление двух заблуждений». Практическая оценка, исследования и оценка . 18 (11).
21. «Напоминание о выводе EViews» (PDF) . Проверено 28 декабря 2020 г.
22. Хаяши (2000, стр. 27, 30)
23. Хаяши (2000, стр. 27)
24. Амемия, Такеши (1985). Продвинутая эконометрика . Издательство Гарвардского университета. п. 13. ISBN 9780674005600.
25. Амемия (1985, стр. 14)
26. Рао, CR (1973). Линейный статистический вывод и его приложения (второе изд.). Нью-Йорк: Дж. Уайли и сыновья. п. 319. ИСБН 0-471-70823-2.
27. Амемия (1985, стр. 20)
28. Амемия (1985, стр. 27)
29. Дэвидсон, Рассел; Маккиннон, Джеймс Г. (1993). Оценка и вывод в эконометрике . Нью-Йорк: Издательство Оксфордского университета. п. 33. ISBN 0-19-506011-3.
30. Дэвидсон и Маккиннон (1993, стр. 36)
31. Дэвидсон и Маккиннон (1993, стр. 20)
32. Амемия (1985, стр. 21)
33. Амемия (1985, стр. 22)
34. Бернэм, Кеннет П.; Дэвид Андерсон (2002). Выбор модели и многомодельный вывод (2-е изд.). Спрингер. ISBN 0-387-95364-7.

дальнейшее чтение

• Догерти, Кристофер (2002). Введение в эконометрику (2-е изд.). Нью-Йорк: Издательство Оксфордского университета. стр. 48–113. ISBN 0-19-877643-8.
• Гуджарати, Дамодар Н .; Портер, Дон К. (2009). Базовая экономика (Пятое изд.). Бостон: МакГроу-Хилл Ирвин. стр. 55–96. ISBN 978-0-07-337577-9.
• Привет, Кристиан; Бур, Пол; Фрэнсис, Филип Х.; Клок, Теун; ван Дейк, Герман К. (2004). Эконометрические методы с применением в бизнесе и экономике (1-е изд.). Оксфорд: Издательство Оксфордского университета. стр. 76–115. ISBN 978-0-19-926801-6.
• Хилл, Р. Картер; Гриффитс, Уильям Э.; Лим, Гуай К. (2008). Принципы эконометрики (3-е изд.). Хобокен, Нью-Джерси: John Wiley & Sons. стр. 8–47. ISBN 978-0-471-72360-8.
• Вулдридж, Джеффри (2008). «Простая модель регрессии». Вводная эконометрика: современный подход (4-е изд.). Мейсон, Огайо: Cengage Learning. стр. 22–67. ISBN 978-0-324-58162-1.