В геодезии фигурой Земли называют размер и форму, используемые для моделирования планеты Земля . Вид фигуры зависит от применения, включая точность, необходимую для модели. Сферическая Земля — это хорошо известное историческое приближение, удовлетворительное для географии , астрономии и многих других целей. Было разработано несколько моделей с большей точностью (включая эллипсоид ), чтобы системы координат могли служить точным потребностям навигации , геодезии , кадастра , землепользования и различных других задач.
Топографическая поверхность Земли отличается разнообразием форм суши и водных акваторий. Эта топографическая поверхность обычно интересует топографов, гидрографов и геофизиков . Хотя это поверхность, на которой проводятся земные измерения, математическое моделирование ее с учетом неровностей было бы чрезвычайно сложным.
Пифагорейская концепция сферической Земли предлагает простую поверхность , с которой легко справиться математически. Во многих астрономических и навигационных вычислениях сфера используется для моделирования Земли как близкого приближения. Однако для измерения расстояний и площадей в масштабе, выходящем за рамки чисто местного, необходима более точная цифра. Лучшие аппроксимации можно получить, моделируя всю поверхность как сплюснутый сфероид , используя сферические гармоники для аппроксимации геоида или моделируя область с помощью наиболее подходящего опорного эллипсоида .
Для съемки небольших территорий достаточно плоской (плоской) модели поверхности Земли, поскольку местная топография подавляет кривизну. Съемки с помощью планшета проводятся на относительно небольших территориях без учета размера и формы всей Земли. Например, таким образом можно провести обследование города.

К концу 1600-х годов серьезные усилия были направлены на моделирование Земли как эллипсоида, начиная с измерения Жаном Пикаром дуги вдоль парижского меридиана . Эти первые попытки мотивировались усовершенствованными картами и более точным измерением расстояний и площадей национальных территорий. В последующие столетия геодезические приборы и методы совершенствовались. Модели по фигуре Земли совершенствовались шаг за шагом.
В середине-конце 20-го века исследования в области наук о Земле способствовали радикальному улучшению точности изображения Земли. Основная польза этой повышенной точности заключалась в предоставлении географических и гравитационных данных для инерциальных систем наведения баллистических ракет . Это финансирование также способствовало расширению геонаучных дисциплин, способствуя созданию и росту различных кафедр геонаучных исследований во многих университетах. [1] Эти разработки также принесли пользу многим гражданским направлениям, таким как управление погодой и спутниками связи, а также определение местоположения с помощью GPS , что было бы невозможно без высокоточных моделей формы Земли.
Модели фигуры Земли различаются по способу их использования, по сложности и по точности, с которой они представляют размер и форму Земли.
.JPG/440px-Horizon,_Valencia_(Spain).JPG)
Простейшей моделью формы всей Земли является сфера. Радиус Земли — это расстояние от центра Земли до ее поверхности, около 6371 км (3959 миль). Хотя «радиус» обычно является характеристикой идеальных сфер, Земля отклоняется от сферической лишь на треть процента, что достаточно близко, чтобы во многих контекстах рассматривать ее как сферу и оправдывает термин «радиус Земли».
Концепция сферической Земли возникла примерно в 6 веке до нашей эры , [2] но оставалась предметом философских спекуляций до 3 века до нашей эры . Первая научная оценка радиуса Земли была дана Эратосфеном около 240 г. до н.э., при этом точность измерений Эратосфена оценивалась в диапазоне от -1% до 15%.
Земля имеет лишь приблизительно сферическую форму, поэтому ни одно значение не может служить ее естественным радиусом. Расстояния от точек на поверхности до центра варьируются от 6353 км (3948 миль) до 6384 км (3967 миль). Каждый из нескольких различных способов моделирования Земли как сферы дает средний радиус 6371 км (3959 миль). Независимо от модели, любой радиус попадает между полярным минимумом около 6357 км (3950 миль) и экваториальным максимумом около 6378 км (3963 миль). Разница в 21 км (13 миль) соответствует тому, что полярный радиус примерно на 0,3% короче экваториального радиуса.

Поскольку Земля уплощена у полюсов и выпукла у экватора , геодезия представляет фигуру Земли в виде сплюснутого сфероида . Сплюснутый сфероид, или сплющенный эллипсоид , представляет собой эллипсоид вращения , полученный вращением эллипса вокруг его более короткой оси. Это правильная геометрическая форма, которая наиболее близко приближается к форме Земли. Сфероид, описывающий фигуру Земли или другого небесного тела, называется опорным эллипсоидом . Отсчетный эллипсоид Земли называется земным эллипсоидом .
Эллипсоид вращения однозначно определяется двумя величинами. В геодезии используются несколько условных обозначений для выражения этих двух величин, но все они эквивалентны и конвертируемы друг в друга:
Эксцентриситет и сплющивание — это разные способы выразить степень сжатия эллипсоида. Когда сплющивание выступает в качестве одной из определяющих величин в геодезии, обычно оно выражается через обратную величину. Например, в сфероиде WGS 84 , используемом современными системами GPS, величина, обратная сглаживанию , равна точно 298,257 223 563 .
Разница между сферой и эталонным эллипсоидом для Земли невелика, всего лишь одна часть из 300. Исторически сплющивание рассчитывалось на основе измерений уклона . В настоящее время используются геодезические сети и спутниковая геодезия . На практике многие опорные эллипсоиды создавались на протяжении веков на основе различных исследований. Значение сглаживания незначительно варьируется от одного опорного эллипсоида к другому, отражая местные условия и то, предназначен ли опорный эллипсоид для моделирования всей Земли или только некоторой ее части.
Сфера имеет единственный радиус кривизны , который является просто радиусом сферы. Более сложные поверхности имеют радиусы кривизны, которые различаются по поверхности. Радиус кривизны описывает радиус сферы, которая лучше всего аппроксимирует поверхность в этой точке. Сплющенные эллипсоиды имеют постоянный радиус кривизны с востока на запад вдоль параллелей , если на поверхности нарисована сетка , но изменяющуюся кривизну в любом другом направлении. У сплюснутого эллипсоида полярный радиус кривизны больше экваториального.
потому что полюс уплощен: чем более плоская поверхность, тем больше должна быть сфера, чтобы приблизиться к ней. И наоборот, радиус кривизны эллипсоида с севера на юг на экваторе меньше, чем полярный.
где – расстояние от центра эллипсоида до экватора (большой полуоси), – расстояние от центра до полюса. (малая полуось)


Ранее было сказано, что измерения производятся на видимой или топографической поверхности Земли, и только что было объяснено, что вычисления производятся на эллипсоиде. В геодезических измерениях участвует еще одна поверхность: геоид . При геодезической съемке вычисление геодезических координат точек обычно выполняется на эталонном эллипсоиде , близком к размеру и форме Земли в районе съемки. Однако фактические измерения, сделанные на поверхности Земли с помощью определенных инструментов, относятся к геоиду. Эллипсоид — это математически определенная правильная поверхность определенных размеров. Геоид, с другой стороны, совпадает с той поверхностью, которой соответствовали бы океаны по всей Земле, если бы они могли приспосабливаться к совокупному эффекту притяжения массы Земли ( гравитации ) и центробежной силы вращения Земли . В результате неравномерного распределения массы Земли поверхность геоида является нерегулярной, и, поскольку эллипсоид представляет собой правильную поверхность, расстояния между ними, называемые волнами геоида , высотами геоида или расстояниями между геоидами, будут нерегулярными, как хорошо.
Геоид — поверхность, вдоль которой гравитационный потенциал всюду равен и к которой направление силы тяжести всегда перпендикулярно (см. Эквипотенциальная поверхность ). Последнее особенно важно, поскольку для проведения геодезических измерений обычно используются оптические приборы, содержащие гравитационно-нивелирные устройства. При правильной настройке вертикальная ось инструмента совпадает с направлением силы тяжести и, следовательно, перпендикулярна геоиду. Угол между отвесом , перпендикулярным геоиду (иногда называемым «вертикалью»), и перпендикуляром к эллипсоиду (иногда называемым «эллипсоидальной нормалью») определяется как отклонение вертикали . Он состоит из двух компонентов: компонента восток-запад и компонент север-юг. [3]
Современная геодезия имеет тенденцию сохранять эллипсоид вращения в качестве эталонного эллипсоида и рассматривать трехосность и грушевидную форму как часть фигуры геоида : они представлены сферическими гармоническими коэффициентами и соответственно соответствующими степени и порядковым номерам 2.2 для трехосности и 3.0 для грушевидной формы.
Возможность того, что экватор Земли лучше характеризовать как эллипс, а не как круг, и, следовательно, что эллипсоид является трехосным, была предметом научных исследований в течение многих лет. [4] [5] Современные технологические разработки предоставили новые и быстрые методы сбора данных, и с момента запуска Спутника-1 орбитальные данные использовались для исследования теории эллиптичности. [3] Более поздние результаты показывают, что разница между двумя экваториальными большой и малой осями инерции составляет 70 м, причем больший полудиаметр указывает на 15 ° западной долготы (а также на 180 градусов от нее). [6] [7]
Теория слегка грушевидной формы Земли возникла и получила известность после того, как первые искусственные спутники наблюдали длительные периодические изменения орбиты, свидетельствующие о депрессии на Южном полюсе и выпуклости такой же степени на Северном полюсе . Эта теория утверждает, что северные средние широты слегка сплющены, а южные средние широты соответственно выпуклы. [3] Данные американского спутника Vanguard 1 за 1958 год подтверждают, что южная экваториальная выпуклость больше, чем северная, что подтверждается тем, что уровень моря на Южном полюсе ниже, чем на севере. [8] Грушевидная форма Земли впервые была высказана в 1498 году Христофором Колумбом на основе его неправильных показаний суточного движения Полярной звезды . [9]
Джону А. О'Кифу и соавторам приписывают открытие того, что Земля имеет значительную зональную сферическую гармонику третьей степени в своем гравитационном поле с использованием данных спутника Vanguard 1. [10] На основании дополнительных данных спутниковой геодезии Десмонд Кинг-Хеле уточнил оценку до разницы в 45 м между северным и южным полярными радиусами из-за 19-метрового подъема «ствола» на Северном полюсе и 26-метровой депрессии на Южном полюсе. Полюс. [11] [12] Однако полярная асимметрия невелика: она примерно в тысячу раз меньше, чем сплющивание Земли, и даже меньше, чем геоидальная волнистость в некоторых регионах Земли. [13]
Возможны более простые локальные аппроксимации.
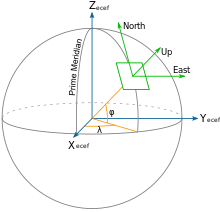
Локальная касательная плоскость подходит для очень малых расстояний.

Наилучшим локальным сферическим приближением эллипсоида вблизи данной точки является соприкасающаяся сфера Земли . Его радиус равен гауссовскому радиусу кривизны Земли , а радиальное направление совпадает с геодезическим нормальным направлением. Центр соприкасающейся сферы смещен от центра эллипсоида, но находится в центре кривизны данной точки на поверхности эллипсоида. Эта концепция помогает интерпретировать результаты измерений рефракции радиозатменного радиосигнала на Земле и планетах , а также в некоторых приложениях навигации и наблюдения. [14] [15]
Определение точной фигуры Земли является не только геометрической задачей геодезии, но имеет и геофизические соображения. Согласно теоретическим рассуждениям Исаака Ньютона , Леонарда Эйлера и других, тело, имеющее однородную плотность 5515 кг/м 3 и вращающееся подобно Земле, должно иметь уплощение 1:229. К такому выводу можно прийти без какой-либо информации о составе недр Земли . [16] Однако измеренное сплющивание составляет 1:298,25, что ближе к сфере и является веским аргументом в пользу того, что ядро Земли чрезвычайно компактно. Следовательно, плотность должна быть функцией глубины и колебаться от 2600 кг/м 3 на поверхности (плотность породы гранита и т. д.) до 13 000 кг/м 3 внутри внутреннего ядра. [17]
Также для физического исследования недр Земли имеет значение гравитационное поле , которое представляет собой совокупный эффект гравитации (из-за притяжения массы) и центробежной силы (из-за вращения). Его можно очень точно измерить на поверхности и дистанционно с помощью спутников. Истинная вертикаль вообще не соответствует теоретической вертикали ( диапазон отклонения до 50"), поскольку топография и все геологические массы нарушают гравитационное поле. Поэтому общее строение земной коры и мантии можно определить с помощью геодезико-геофизических моделей недр. .
![]() В эту статью включен текст из источника, находящегося в свободном доступе : Агентство оборонных карт (1983). Геодезия для непрофессионала (Отчет). ВВС США.
В эту статью включен текст из источника, находящегося в свободном доступе : Агентство оборонных карт (1983). Геодезия для непрофессионала (Отчет). ВВС США.