
В математике ноль — это четное число . Другими словами, его четность — свойство целого числа быть четным или нечетным — четная. Это можно легко проверить, исходя из определения «четного»: это целое число, кратное 2 , а именно 0 × 2. В результате ноль обладает всеми свойствами, характеризующими четные числа: например, 0 соседствует с обеих сторон с нечетными числами, любое десятичное целое число имеет ту же четность, что и его последняя цифра, — так что, поскольку 10 четное, 0 будет четным, а если y четное, то y + x имеет ту же четность, что и x, — действительно, 0 + x и x всегда имеют одинаковую четность.
Ноль также вписывается в шаблоны, образованные другими четными числами. Правила четности арифметики, такие как чет − чет = чет , требуют, чтобы 0 был четным. Ноль является элементом аддитивной идентичности группы четных целых чисел, и это начальный случай, из которого рекурсивно определяются другие четные натуральные числа . Приложения этой рекурсии из теории графов в вычислительную геометрию основаны на том, что ноль является четным. 0 не только делится на 2, он делится на каждую степень 2 , что имеет отношение к двоичной системе счисления, используемой компьютерами. В этом смысле 0 является «самым четным» числом из всех. [1]
Среди широкой общественности четность нуля может стать источником путаницы. В экспериментах на время реакции большинство людей медленнее определяют 0 как четное число, чем 2, 4, 6 или 8. Некоторые учителя и некоторые дети на уроках математики думают, что ноль является нечетным числом, или одновременно четным и нечетным, или ни тем, ни другим. Исследователи в области математического образования предполагают, что эти заблуждения могут стать возможностями для обучения. Изучение равенств, таких как 0 × 2 = 0, может развеять сомнения учащихся относительно того, чтобы называть 0 числом и использовать его в арифметике . Обсуждения в классе могут помочь учащимся оценить основные принципы математического мышления, такие как важность определений. Оценка четности этого исключительного числа является ранним примером распространенной темы в математике: абстракция знакомого понятия в незнакомой обстановке.
Стандартное определение «четного числа» может быть использовано для прямого доказательства того, что ноль — четное число. Число называется «четным», если оно является целым числом, кратным 2. Например, причина того, что 10 является четным, заключается в том, что оно равно 5 × 2. Точно так же ноль является целым числом, кратным 2, а именно 0 × 2, поэтому ноль — четное число. [2]
Также возможно объяснить, почему ноль четный, не прибегая к формальным определениям. [3] Следующие объяснения придают смысл идее о том, что ноль четный, с точки зрения фундаментальных числовых понятий. На этой основе можно дать обоснование самого определения — и его применимости к нулю.

При наличии набора объектов используется число, чтобы описать, сколько объектов находится в наборе. Ноль — это количество нулевых объектов ; в более формальных терминах это количество объектов в пустом наборе . Концепция четности используется для создания групп из двух объектов. Если объекты в наборе можно разбить на группы по два, и ничего не останется, то количество объектов четное. Если объект остается, то количество объектов нечетное. Пустой набор содержит ноль групп по два, и от этой группировки не остается ни одного объекта, поэтому ноль — четное число. [5]
Эти идеи можно проиллюстрировать, рисуя объекты парами. Трудно изобразить нулевые группы из двух или подчеркнуть отсутствие оставшегося объекта, поэтому полезно нарисовать другие группировки и сравнить их с нулем. Например, в группе из пяти объектов есть две пары. Что еще важнее, есть оставшийся объект, поэтому 5 — нечетное число. В группе из четырех объектов нет оставшегося объекта, поэтому 4 — четное число. В группе из одного объекта нет пар, и есть оставшийся объект, поэтому 1 — нечетное число. В группе из нуля объектов нет оставшегося объекта, поэтому 0 — четное число. [6]
Есть еще одно конкретное определение четности: если объекты в наборе можно поместить в две группы одинакового размера, то количество объектов четное. Это определение эквивалентно первому. Опять же, ноль четный, потому что пустой набор можно разделить на две группы по ноль элементов в каждой. [7]
Числа также можно визуализировать как точки на числовой прямой . Когда четные и нечетные числа различаются, их закономерность становится очевидной, особенно если включены отрицательные числа:

Чётные и нечётные числа чередуются. Начиная с любого чётного числа, отсчёт вверх или вниз по двойкам достигает других чётных чисел, и нет причин перескакивать через ноль. [8]
С введением умножения четность может быть достигнута более формальным способом с использованием арифметических выражений. Каждое целое число имеет вид (2 × ▢) + 0 или (2 × ▢) + 1; первые числа четные, а вторые нечетные. Например, 1 нечетное, потому что 1 = (2 × 0) + 1, а 0 четное, потому что 0 = (2 × 0) + 0. Составление таблицы этих фактов затем подкрепляет рисунок числовой прямой выше. [9]
Точное определение математического термина, такого как «четный», означающего «целое число, кратное двум», в конечном счете является соглашением . В отличие от «четного», некоторые математические термины намеренно построены так, чтобы исключить тривиальные или вырожденные случаи. Известным примером являются простые числа . До 20-го века определения простоты были непоследовательными, и такие выдающиеся математики, как Гольдбах , Ламберт , Лежандр , Кэли и Кронекер, писали, что 1 является простым числом. [10] Современное определение «простого числа» — это «положительное целое число с ровно 2 множителями », поэтому 1 не является простым числом. Это определение можно рационализировать, заметив, что оно более естественно подходит для математических теорем, касающихся простых чисел. Например, фундаментальную теорему арифметики легче сформулировать, когда 1 не считается простым числом. [11]
Можно было бы аналогичным образом переопределить термин «четный» таким образом, чтобы он больше не включал ноль. Однако в этом случае новое определение затруднило бы формулировку теорем, касающихся четных чисел. Эффект уже можно увидеть в алгебраических правилах, управляющих четными и нечетными числами . [12] Наиболее важные правила касаются сложения , вычитания и умножения :
Подставляя соответствующие значения в левые части этих правил, можно получить 0 в правых частях:
Вышеуказанные правила были бы неверными, если бы ноль не был четным. [12] В лучшем случае их пришлось бы изменить. Например, одно руководство по тестированию утверждает, что четные числа характеризуются как целые кратные двух, но ноль не является «ни четным, ни нечетным». [13] Соответственно, правила руководства для четных и нечетных чисел содержат исключения:
Исключение для нуля в определении четности заставляет делать такие исключения в правилах для четных чисел. С другой стороны, принятие правил, которым подчиняются положительные четные числа, и требование, чтобы они продолжали выполняться для целых чисел, заставляет обычное определение и четность нуля. [12]
Бесчисленные результаты в теории чисел ссылаются на фундаментальную теорему арифметики и алгебраические свойства четных чисел, поэтому приведенные выше выборы имеют далеко идущие последствия. Например, тот факт, что положительные числа имеют уникальные факторизации , означает, что можно определить, имеет ли число четное или нечетное количество различных простых множителей. Поскольку 1 не является простым числом и не имеет простых множителей, оно является произведением различных простых чисел; поскольку 0 является четным числом, 1 имеет четное количество различных простых множителей. Это означает, что функция Мёбиуса принимает значение μ(1) = 1 , что необходимо для того, чтобы она была мультипликативной функцией и чтобы работала формула обращения Мёбиуса . [14]
Число n нечетно, если существует целое число k, такое что n = 2 k + 1. Один из способов доказать, что ноль не является нечетным, — это доказать от противного : если 0 = 2 k + 1, то k = −1/2 , что не является целым числом. [15] Поскольку ноль не нечетен, если доказано, что неизвестное число нечетно, то оно не может быть нулем. Это, казалось бы, тривиальное наблюдение может предоставить удобное и показательное доказательство, объясняющее, почему нечетное число не равно нулю.
Классический результат теории графов гласит, что граф нечетного порядка (имеющий нечетное число вершин) всегда имеет по крайней мере одну вершину четной степени . (Само утверждение требует, чтобы ноль был четным: пустой граф имеет четный порядок, а изолированная вершина имеет четную степень.) [16] Чтобы доказать утверждение, на самом деле проще доказать более сильный результат: любой граф нечетного порядка имеет нечетное число вершин четной степени. Появление этого нечетного числа объясняется еще более общим результатом, известным как лемма о рукопожатии : любой граф имеет четное число вершин нечетной степени. [17] Наконец, четное число нечетных вершин естественным образом объясняется формулой суммы степеней .
Лемма Шпернера — это более продвинутое применение той же стратегии. Лемма утверждает, что определенный вид раскраски на триангуляции симплекса имеет подсимплекс, содержащий каждый цвет. Вместо того, чтобы напрямую строить такой подсимплекс , удобнее доказать, что существует нечетное число таких подсимплексов, с помощью индукционного аргумента. [18] Более сильное утверждение леммы затем объясняет, почему это число нечетное: оно естественным образом распадается на ( n + 1) + n , если рассмотреть две возможные ориентации симплекса. [19]
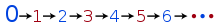
Тот факт, что ноль является четным, вместе с тем фактом, что четные и нечетные числа чередуются, достаточен для определения четности любого другого натурального числа . Эту идею можно формализовать в рекурсивное определение множества четных натуральных чисел:
Это определение имеет концептуальное преимущество, поскольку опирается только на минимальные основы натуральных чисел: существование 0 и последователей . Как таковое, оно полезно для систем компьютерной логики, таких как LF и доказательство теоремы Изабеллы . [20] При таком определении четность нуля является не теоремой, а аксиомой. Действительно, «ноль — четное число» может быть интерпретировано как одна из аксиом Пеано , моделью которой являются четные натуральные числа. [21] Похожая конструкция расширяет определение четности до трансфинитных порядковых чисел : каждый предельный порядковый номер четный, включая ноль, а последователи четных порядковых номеров нечетные. [22]

Классический тест «точка в многоугольнике» из вычислительной геометрии применяет вышеизложенные идеи. Чтобы определить, лежит ли точка внутри многоугольника , нужно пропустить луч из бесконечности в точку и подсчитать количество пересечений луча с краем многоугольника. Число пересечений четно тогда и только тогда, когда точка находится вне многоугольника. Этот алгоритм работает, потому что если луч никогда не пересекает многоугольник, то его число пересечений равно нулю, что четно, и точка находится вне многоугольника. Каждый раз, когда луч пересекает многоугольник, число пересечений чередуется между четным и нечетным, а точка на его кончике чередуется между внешним и внутренним. [23]

В теории графов двудольный граф — это граф, вершины которого разделены на два цвета , так что соседние вершины имеют разные цвета. Если связный граф не имеет нечетных циклов , то двудольное графство может быть построено путем выбора базовой вершины v и раскрашивания каждой вершины в черный или белый цвет в зависимости от того, является ли ее расстояние от v четным или нечетным. Поскольку расстояние между v и собой равно 0, а 0 четно, базовая вершина окрашена иначе, чем ее соседи, которые находятся на расстоянии 1. [24]

В абстрактной алгебре четные целые числа образуют различные алгебраические структуры , требующие включения нуля. Тот факт, что аддитивное тождество (ноль) является четным, вместе с четностью сумм и аддитивных обратных четных чисел и ассоциативностью сложения, означает, что четные целые числа образуют группу . Более того, группа четных целых чисел при сложении является подгруппой группы всех целых чисел; это элементарный пример концепции подгруппы. [16] Более раннее наблюдение, что правило «четный − четный = четный» заставляет 0 быть четным, является частью общей закономерности: любое непустое подмножество аддитивной группы, замкнутое относительно вычитания, должно быть подгруппой и, в частности, должно содержать тождество . [25]
Так как четные целые числа образуют подгруппу целых чисел, они разбивают целые числа на смежные классы . Эти смежные классы можно описать как классы эквивалентности следующего отношения эквивалентности : x ~ y , если ( x − y ) четно. Здесь четность нуля напрямую проявляется как рефлексивность бинарного отношения ~. [26] Существует только два смежных класса этой подгруппы — четные и нечетные числа — поэтому она имеет индекс 2.
Аналогично, знакопеременная группа является подгруппой индекса 2 в симметрической группе из n букв. Элементы знакопеременной группы, называемые четными перестановками , являются произведениями четного числа транспозиций . Тождественное отображение , пустое произведение без транспозиций, является четной перестановкой, поскольку ноль четный; это единичный элемент группы. [27]
Правило "четное × целое = четное" означает, что четные числа образуют идеал в кольце целых чисел, и указанное выше отношение эквивалентности можно описать как эквивалентность по модулю этого идеала . В частности, четные целые числа — это в точности те целые числа k , где k ≡ 0 (mod 2). Эта формулировка полезна для исследования целых нулей многочленов . [28]
В некотором смысле некоторые кратные 2 являются «более четными», чем другие. Числа, кратные 4, называются дважды четными , поскольку их можно разделить на 2 дважды. Ноль не только делится на 4, но и обладает уникальным свойством делиться на любую степень 2 , поэтому он превосходит все другие числа по «четности». [1]
Одно из последствий этого факта проявляется в обратном порядке битов целочисленных типов данных , используемых некоторыми компьютерными алгоритмами, такими как быстрое преобразование Фурье Кули–Тьюки . Этот порядок имеет свойство, что чем левее первая 1 встречается в двоичном расширении числа , или чем больше раз она делится на 2, тем раньше она появляется. Обращение бита нуля по-прежнему равно нулю; его можно разделить на 2 любое количество раз, и его двоичное расширение не содержит никаких единиц, поэтому он всегда идет первым. [29]
Хотя 0 делится на 2 больше раз, чем любое другое число, нелегко точно определить, сколько раз это происходит. Для любого ненулевого целого числа n можно определить 2-адический порядок n как количество раз, которое n делится на 2. Это описание не работает для 0; независимо от того, сколько раз он делится на 2, его всегда можно снова разделить на 2. Вместо этого обычно принято устанавливать 2-порядок 0 равным бесконечности как особый случай. [30] Это соглашение не является специфическим для 2-порядка; это одна из аксиом аддитивной оценки в высшей алгебре. [31]
Степени двойки — 1, 2, 4, 8, ... — образуют простую последовательность чисел возрастающего порядка 2. В 2-адических числах такие последовательности фактически сходятся к нулю. [32]

Тема четности нуля часто рассматривается в течение первых двух-трех лет начального образования , когда вводится и развивается концепция четных и нечетных чисел. [34]
Диаграмма справа [33] отображает убеждения детей о четности нуля по мере их продвижения с 1-го по 6-й год обучения в английской системе образования . Данные предоставлены Леном Фробишером, который провел пару опросов английских школьников. Фробишера интересовало, как знание однозначной четности преобразуется в знание многозначной четности, и ноль занимает видное место в результатах. [35]
В предварительном опросе почти 400 семилетних детей 45% выбрали четное число вместо нечетного , когда их спросили о четности нуля. [36] Последующее исследование предложило больше вариантов: ни один , оба и не знаю . На этот раз количество детей в том же возрастном диапазоне, идентифицирующих ноль как четное, снизилось до 32%. [37] Успешность в решении, что ноль четный, изначально резко возрастает, а затем стабилизируется на уровне около 50% в возрасте от 3 до 6 лет. [38] Для сравнения, самая простая задача, определение четности одной цифры, стабилизируется на уровне около 85% успеха. [39]
В интервью Фробишер выяснял рассуждения студентов. Один пятикурсник решил, что 0 четное число, потому что оно было найдено в таблице умножения на 2. Пара четверокурсников поняли, что ноль можно разделить на равные части. Другой четверокурсник рассуждал: «1 нечетное число, а если я спущусь вниз, то оно будет четным». [40] В интервью также были выявлены заблуждения, стоящие за неправильными ответами. Второкурсник был «совершенно убежден», что ноль нечетное число, на основании того, что «это первое число, которое вы считаете». [41] Четвертокурсник назвал 0 «ничем» и думал, что он не является ни нечетным, ни четным, поскольку «это не число». [42] В другом исследовании Энни Кейт наблюдала за классом из 15 второклассников, которые убеждали друг друга, что ноль — четное число, основываясь на чередовании четных и нечетных чисел и на возможности разделения группы нулей на две равные группы. [43]
Более глубокие исследования были проведены Эстер Левенсон, Пессией Цамир и Диной Тирош, которые взяли интервью у пары учеников шестого класса в США, которые показывали высокие результаты на уроках математики. Один ученик предпочитал дедуктивные объяснения математических утверждений, в то время как другой предпочитал практические примеры. Оба ученика изначально думали, что 0 не является ни четным, ни нечетным, по разным причинам. Левенсон и др. продемонстрировали, как рассуждения учеников отражают их концепции нуля и деления. [44]
Дебора Левенберг Болл проанализировала идеи учеников третьего класса США о четных и нечетных числах и нуле, которые они только что обсуждали с группой учеников четвертого класса. Учащиеся обсуждали четность нуля, правила для четных чисел и то, как делается математика. Заявления о нуле принимали различные формы, как показано в списке справа. [45] Болл и ее соавторы утверждали, что эпизод продемонстрировал, как ученики могут «заниматься математикой в школе», в отличие от обычного сведения дисциплины к механическому решению упражнений. [46]
Одной из тем в исследовательской литературе является напряжение между концептуальными образами учащихся о четности и их концептуальными определениями. [47] Шестиклассники Левенсона и др. оба определили четные числа как кратные 2 или числа, делящиеся на 2, но они изначально не могли применить это определение к нулю, потому что не были уверены, как умножать или делить ноль на 2. Интервьюер в конечном итоге привел их к выводу, что ноль был четным; студенты пошли разными путями к этому выводу, опираясь на комбинацию образов, определений, практических объяснений и абстрактных объяснений. В другом исследовании Дэвид Дикерсон и Дэмиен Питман изучили использование определений пятью студентами - математиками продвинутого уровня . Они обнаружили, что студенты в значительной степени могли применить определение «четного» к нулю, но они все еще не были убеждены этим рассуждением, поскольку оно противоречило их концептуальным образам. [48]
Исследователи математического образования в Мичиганском университете включили подсказку «истина или ложь» «0 — четное число» в базу данных из более чем 250 вопросов, разработанных для оценки знаний учителями содержания. Для них этот вопрос является примером «общепринятого знания..., которое должен иметь любой хорошо образованный взрослый», и он «идеологически нейтрален» в том смысле, что ответ не различается между традиционной и реформированной математикой . В исследовании 2000–2004 годов, проведенном среди 700 учителей начальной школы в Соединенных Штатах , общая успеваемость по этим вопросам значительно предсказывала улучшение результатов стандартизированных тестов учащихся после посещения занятий учителей. [49] В более глубоком исследовании 2008 года исследователи обнаружили школу, где все учителя считали, что ноль не является ни четным, ни нечетным числом, включая одного учителя, который был образцовым по всем остальным показателям. Заблуждение было распространено тренером по математике в их здании. [50]
Неясно, сколько учителей имеют неправильные представления о нуле. Исследования Мичигана не публиковали данные по отдельным вопросам. Бетти Лихтенберг, доцент кафедры математического образования в Университете Южной Флориды , в исследовании 1972 года сообщила, что когда группе будущих учителей начальной школы дали тест «истина или ложь», включающий пункт «Ноль — четное число», они обнаружили, что это «каверзный вопрос», и около двух третей ответили «Ложь». [51]
Математически доказательство того, что ноль является четным, является простым вопросом применения определения, но в контексте образования требуется больше объяснений. Одна из проблем касается основ доказательства; определение «четного» как «целого числа, кратного 2» не всегда уместно. Ученик в первые годы начального образования, возможно, еще не узнал, что означает «целое число» или «кратное», не говоря уже о том, как умножать на 0. [52] Кроме того, указание определения четности для всех целых чисел может показаться произвольным концептуальным сокращением, если единственные четные числа, исследованные до сих пор, были положительными. Может помочь признание того, что, поскольку концепция числа расширяется от положительных целых чисел, чтобы включить ноль и отрицательные целые числа, свойства числа, такие как четность, также расширяются нетривиальным образом. [53]

Взрослые, которые верят, что ноль — это четное число, тем не менее, могут быть незнакомы с тем, чтобы думать о нем как о четном числе, достаточно, чтобы заметно замедлить их в эксперименте на время реакции . Станислас Дехане , пионер в области числового познания , провел серию таких экспериментов в начале 1990-х годов. Цифра высвечивается на мониторе субъекта , и компьютер регистрирует время, которое требуется субъекту, чтобы нажать одну из двух кнопок, чтобы определить, является ли число нечетным или четным. Результаты показали, что 0 обрабатывается медленнее, чем другие четные числа. Некоторые вариации эксперимента обнаружили задержки до 60 миллисекунд или около 10% от среднего времени реакции — небольшая разница, но существенная. [55]
Эксперименты Дехейна не были специально разработаны для исследования 0, а для сравнения конкурирующих моделей того, как обрабатывается и извлекается информация о четности. Наиболее конкретная модель, гипотеза ментального расчета, предполагает, что реакции на 0 должны быть быстрыми; 0 — небольшое число, и легко вычислить 0 × 2 = 0. (Известно, что субъекты вычисляют и называют результат умножения на ноль быстрее, чем умножение ненулевых чисел, хотя они медленнее проверяют предложенные результаты, такие как 2 × 0 = 0. ) Результаты экспериментов предполагали, что происходит что-то совсем другое: информация о четности, по-видимому, извлекается из памяти вместе с кластером связанных свойств, таких как простота или степень двойки . Как последовательность степеней двойки, так и последовательность положительных четных чисел 2, 4, 6, 8, ... являются хорошо различимыми ментальными категориями, члены которых прототипически четные. Ноль не принадлежит ни к одному из списков, отсюда и более медленные ответы. [56]
Повторные эксперименты показали задержку на нуле у испытуемых с различным возрастом, национальным и языковым происхождением, которым сталкивались с названиями чисел в числовой форме, прописанными и написанными в зеркальном отображении. Группа Дехане обнаружила один отличительный фактор: математические знания. В одном из своих экспериментов студенты École Normale Supérieure были разделены на две группы: тех, кто изучал литературу, и тех, кто изучал математику, физику или биологию. Замедление на 0 было «в основном обнаружено в [литературной] группе», и на самом деле «до эксперимента некоторые испытуемые L не были уверены, является ли 0 четным или нечетным, и им приходилось напоминать о математическом определении». [57]
Эта сильная зависимость от знакомства снова подрывает гипотезу ментального расчета. [58] Эффект также предполагает, что нецелесообразно включать ноль в эксперименты, где четные и нечетные числа сравниваются как группа. Как говорится в одном исследовании, «большинство исследователей, похоже, согласны с тем, что ноль не является типичным четным числом и не должен исследоваться как часть ментальной числовой линии». [59]
Некоторые контексты, в которых появляется четность нуля, являются чисто риторическими. Лингвист Джозеф Граймс размышляет о том, что вопрос «Является ли ноль четным числом?» супружеским парам — это хороший способ заставить их не соглашаться. [60] Люди, которые думают, что ноль не является ни четным, ни нечетным, могут использовать четность нуля как доказательство того, что каждое правило имеет контрпример , [61] или как пример вопроса с подвохом . [62]
Около 2000 года средства массовой информации отметили пару необычных вех: «1999/11/19» была последней календарной датой, состоящей из всех нечетных цифр, которая встречалась в течение очень долгого времени, и что «2000/02/02» была первой полностью четной датой, которая встречалась в течение очень долгого времени. [63] Поскольку эти результаты используют 0 как четное число, некоторые читатели не согласились с этой идеей. [64]
В стандартизированных тестах , если вопрос касается поведения четных чисел, может потребоваться помнить, что ноль — четное число. [65] В официальных публикациях, касающихся тестов GMAT и GRE, указано, что 0 — четное число. [66]
Четность нуля имеет отношение к четно-нечетному нормированию , при котором автомобили могут ездить или покупать бензин в альтернативные дни в соответствии с четностью последней цифры в их номерных знаках . Половина чисел в заданном диапазоне заканчивается на 0, 2, 4, 6, 8, а другая половина на 1, 3, 5, 7, 9, поэтому имеет смысл включать 0 с другими четными числами. Однако в 1977 году парижская система нормирования привела к путанице: в нечетный день полиция избегала штрафовать водителей, чьи номера заканчивались на 0, потому что они не знали, является ли 0 четным. [67] Чтобы избежать такой путаницы, соответствующее законодательство иногда предусматривает, что ноль является четным; такие законы были приняты в Новом Южном Уэльсе [68] и Мэриленде [69] .
На судах ВМС США четные отсеки находятся на левом борту, но ноль зарезервирован для отсеков, которые пересекают центральную линию. То есть, номера читаются как 6-4-2-0-1-3-5 от левого борта к правому. [70]
В игре в рулетку число 0 не считается четным или нечетным, что дает казино преимущество в таких ставках. [71] Аналогично, четность нуля может влиять на выплаты в дополнительных ставках , когда результат зависит от того, является ли некоторое случайное число четным или нечетным, и оно оказывается равным нулю. [72]
Игра « чет-нечет » также затрагивается: если оба игрока выкинули ноль пальцев, общее количество пальцев равно нулю, поэтому выигрывает игрок, выкинувший четное число. [73] В одном руководстве для учителей предлагается играть в эту игру, чтобы познакомить детей с концепцией того, что 0 делится на 2. [74]
{{citation}}: CS1 maint: числовые имена: список авторов ( ссылка ){{citation}}: CS1 maint: числовые имена: список авторов ( ссылка )