Двойное пространство

В математике векторное пространство линейных форм

В математике любому векторному пространству соответствует дуальное векторное пространство (или просто дуальное пространство для краткости), состоящее из всех линейных форм на , а также структуры векторного пространства поточечного сложения и скалярного умножения на константы. ${\displaystyle V}$ ${\displaystyle V,}$

Двойственное пространство, как определено выше, определено для всех векторных пространств, и во избежание двусмысленности может также называться алгебраическим двойственным пространством . При определении для топологического векторного пространства существует подпространство двойственного пространства, соответствующее непрерывным линейным функционалам , называемое непрерывным двойственным пространством .

Дуальные векторные пространства находят применение во многих разделах математики, которые используют векторные пространства, например, в тензорном анализе с конечномерными векторными пространствами. Применительно к векторным пространствам функций (которые обычно бесконечномерны) дуальные пространства используются для описания мер , распределений и гильбертовых пространств . Следовательно, дуальное пространство является важным понятием в функциональном анализе .

Ранние термины для дуального включают polarer Raum [Hahn 1927], espace conjugué , adjoint space [Alaoglu 1940] и transponierter Raum [Schauder 1930] и [Banach 1932]. Термин дуальный появился благодаря Бурбаки 1938. ^[1]

Алгебраическое дуальное пространство

Для любого векторного пространства над полем (алгебраическое) сопряженное пространство [ ^2] (альтернативно обозначаемое как ^[3] или ^{[4] [5]} ) ^{[nb 1]} определяется как множество всех линейных отображений ( линейных функционалов ). Поскольку линейные отображения являются гомоморфизмами векторного пространства , сопряженное пространство может быть обозначено как . ^[3] Само сопряженное пространство становится векторным пространством над , если снабжено сложением и скалярным умножением, удовлетворяющими: ${\displaystyle V}$ ${\displaystyle F}$ ${\displaystyle V^{*}}$ ${\displaystyle V^{\lor }}$ ${\displaystyle V'}$ ${\displaystyle \varphi :V\to F}$ ${\displaystyle \hom(V,F)}$ ${\displaystyle V^{*}}$ ${\displaystyle F}$

${\displaystyle {\begin{aligned}(\varphi +\psi )(x)&=\varphi (x)+\psi (x)\\(a\varphi )(x)&=a\left(\varphi (x)\right)\end{aligned}}}$

для всех , , и . ${\displaystyle \varphi ,\psi \in V^{*}}$ ${\displaystyle x\in V}$ ${\displaystyle a\in F}$

Элементы алгебраического двойственного пространства иногда называют ковекторами , один-формами или линейными формами . ${\displaystyle V^{*}}$

Спаривание функционала в двойственном пространстве и элемента иногда обозначается скобкой: ^[6] или . ^[7] Это спаривание определяет невырожденное билинейное отображение ^{[nb 2],} называемое естественным спариванием . ${\displaystyle \varphi }$ ${\displaystyle V^{*}}$ ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle \varphi (x)=[x,\varphi ]}$ ${\displaystyle \varphi (x)=\langle x,\varphi \rangle }$ ${\displaystyle \langle \cdot ,\cdot \rangle :V\times V^{*}\to F}$

Конечномерный случай

Если конечномерно, то имеет ту же размерность, что и . При наличии базиса в можно построить определенный базис в , называемый дуальным базисом . Этот дуальный базис представляет собой набор линейных функционалов на , определяемый соотношением ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle \{\mathbf {e} _{1},\dots ,\mathbf {e} _{n}\}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle \{\mathbf {e} ^{1},\dots ,\mathbf {e} ^{n}\}}$ ${\displaystyle V}$

${\displaystyle \mathbf {e} ^{i}(c^{1}\mathbf {e} _{1}+\cdots +c^{n}\mathbf {e} _{n})=c^{i},\quad i=1,\ldots ,n}$

для любого выбора коэффициентов . В частности, если поочередно приравнять каждый из этих коэффициентов к единице, а остальные коэффициенты — к нулю, то получим систему уравнений ${\displaystyle c^{i}\in F}$

${\displaystyle \mathbf {e} ^{i}(\mathbf {e} _{j})=\delta _{j}^{i}}$

где — символ дельта Кронекера . Это свойство называется свойством биортогональности . ${\displaystyle \delta _{j}^{i}}$

Например, если есть , пусть его базис будет выбран как . Базисные векторы не ортогональны друг другу. Тогда и являются одноформами (функциями, которые отображают вектор в скаляр) такими, что , , , и . (Примечание: верхний индекс здесь — это индекс, а не показатель степени.) Эту систему уравнений можно выразить с помощью матричной записи как ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{2}}$ ${\displaystyle \{\mathbf {e} _{1}=(1/2,1/2),\mathbf {e} _{2}=(0,1)\}}$ ${\displaystyle \mathbf {e} ^{1}}$ ${\displaystyle \mathbf {e} ^{2}}$ ${\displaystyle \mathbf {e} ^{1}(\mathbf {e} _{1})=1}$ ${\displaystyle \mathbf {e} ^{1}(\mathbf {e} _{2})=0}$ ${\displaystyle \mathbf {e} ^{2}(\mathbf {e} _{1})=0}$ ${\displaystyle \mathbf {e} ^{2}(\mathbf {e} _{2})=1}$

${\displaystyle {\begin{bmatrix}e^{11}&e^{12}\\e^{21}&e^{22}\end{bmatrix}}{\begin{bmatrix}e_{11}&e_{21}\\e_{12}&e_{22}\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}.}$

Решение для неизвестных значений в первой матрице показывает, что двойственный базис равен . Поскольку и являются функционалами, их можно переписать как и . ${\displaystyle \{\mathbf {e} ^{1}=(2,0),\mathbf {e} ^{2}=(-1,1)\}}$ ${\displaystyle \mathbf {e} ^{1}}$ ${\displaystyle \mathbf {e} ^{2}}$ ${\displaystyle \mathbf {e} ^{1}(x,y)=2x}$ ${\displaystyle \mathbf {e} ^{2}(x,y)=-x+y}$

В общем случае , если — матрица, столбцы которой являются базисными векторами, а — матрица, столбцы которой являются двойственными базисными векторами, то ${\displaystyle V}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle E=[\mathbf {e} _{1}|\cdots |\mathbf {e} _{n}]}$ ${\displaystyle {\hat {E}}=[\mathbf {e} ^{1}|\cdots |\mathbf {e} ^{n}]}$

${\displaystyle {\hat {E}}^{\textrm {T}}\cdot E=I_{n},}$

где — единичная матрица порядка . Свойство биортогональности этих двух базисных множеств позволяет представить любую точку в виде ${\displaystyle I_{n}}$ ${\displaystyle n}$ ${\displaystyle \mathbf {x} \in V}$

${\displaystyle \mathbf {x} =\sum _{i}\langle \mathbf {x} ,\mathbf {e} ^{i}\rangle \mathbf {e} _{i}=\sum _{i}\langle \mathbf {x} ,\mathbf {e} _{i}\rangle \mathbf {e} ^{i},}$

даже когда базисные векторы не ортогональны друг другу. Строго говоря, приведенное выше утверждение имеет смысл только после введения скалярного произведения и соответствующего дуального спаривания, как описано ниже в § Билинейные произведения и дуальные пространства . ${\displaystyle \langle \cdot ,\cdot \rangle }$

В частности, может быть интерпретировано как пространство столбцов действительных чисел , его дуальное пространство обычно записывается как пространство строк действительных чисел. Такая строка действует на как линейный функционал с помощью обычного умножения матриц . Это потому, что функционал отображает каждый -вектор в действительное число . Затем, рассматривая этот функционал как матрицу , и как матрицу, и матрицу (тривиально, действительное число) соответственно, если тогда, по соображениям размерности, должен быть матрицей; то есть должен быть вектором-строкой. ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle n}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle n\times 1}$ ${\displaystyle y}$ ${\displaystyle 1\times 1}$ ${\displaystyle Mx=y}$ ${\displaystyle M}$ ${\displaystyle 1\times n}$ ${\displaystyle M}$

Если состоит из пространства геометрических векторов на плоскости, то кривые уровня элемента из образуют семейство параллельных прямых в , поскольку диапазон одномерен, так что каждая точка в диапазоне является кратной любому одному ненулевому элементу. Таким образом, элемент из можно интуитивно рассматривать как определенное семейство параллельных прямых, покрывающих плоскость. Чтобы вычислить значение функционала на заданном векторе, достаточно определить, на какой из прямых лежит вектор. Неформально, это «подсчитывает», сколько прямых пересекает вектор. В более общем смысле, если — векторное пространство любой размерности, то множества уровня линейного функционала в являются параллельными гиперплоскостями в , и действие линейного функционала на вектор можно визуализировать в терминах этих гиперплоскостей. ^[8] ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$ ${\displaystyle V^{*}}$ ${\displaystyle V}$

Бесконечномерный случай

Если не является конечномерным, но имеет базис ^{[nb 3],} индексированный бесконечным множеством , то та же конструкция, что и в конечномерном случае, дает линейно независимые элементы ( ) сопряженного пространства, но они не будут образовывать базис. ${\displaystyle V}$ ${\displaystyle \mathbf {e} _{\alpha }}$ ${\displaystyle A}$ ${\displaystyle \mathbf {e} ^{\alpha }}$ ${\displaystyle \alpha \in A}$

Например, рассмотрим пространство , элементами которого являются последовательности действительных чисел, содержащие только конечное число ненулевых элементов, которое имеет базис, индексированный натуральными числами . Для , — это последовательность, состоящая из всех нулей, за исключением -й позиции, которая равна 1. Двойственное пространство для — это (изоморфно) , пространство всех последовательностей действительных чисел: каждая действительная последовательность определяет функцию, где элемент из отправляется в число ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {N} }$ ${\displaystyle i\in \mathbb {N} }$ ${\displaystyle \mathbf {e} _{i}}$ ${\displaystyle i}$ ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle (a_{n})}$ ${\displaystyle (x_{n})}$ ${\displaystyle \mathbb {R} ^{\infty }}$

${\displaystyle \sum _{n}a_{n}x_{n},}$

что является конечной суммой, поскольку существует лишь конечное число ненулевых . Размерность является счетно бесконечной , тогда как не имеет счетного базиса. ${\displaystyle x_{n}}$ ${\displaystyle \mathbb {R} ^{\infty }}$ ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$

Это наблюдение обобщается на любое ^{[nb 3]} бесконечномерное векторное пространство над любым полем : выбор базиса отождествляется с пространством функций, таких, что является ненулевым только для конечного числа , где такая функция отождествляется с вектором ${\displaystyle V}$ ${\displaystyle F}$ ${\displaystyle \{\mathbf {e} _{\alpha }:\alpha \in A\}}$ ${\displaystyle V}$ ${\displaystyle (F^{A})_{0}}$ ${\displaystyle f:A\to F}$ ${\displaystyle f_{\alpha }=f(\alpha )}$ ${\displaystyle \alpha \in A}$ ${\displaystyle f}$

${\displaystyle \sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }}$

в (сумма конечна по предположению о , и любое может быть записано таким образом однозначно по определению базиса). ${\displaystyle V}$ ${\displaystyle f}$ ${\displaystyle v\in V}$

Двойственное пространство может быть тогда отождествлено с пространством всех функций от до : линейный функционал на однозначно определяется значениями, которые он принимает на основе , и любая функция (с ) определяет линейный функционал на с помощью ${\displaystyle V}$ ${\displaystyle F^{A}}$ ${\displaystyle A}$ ${\displaystyle F}$ ${\displaystyle T}$ ${\displaystyle V}$ ${\displaystyle \theta _{\alpha }=T(\mathbf {e} _{\alpha })}$ ${\displaystyle V}$ ${\displaystyle \theta :A\to F}$ ${\displaystyle \theta (\alpha )=\theta _{\alpha }}$ ${\displaystyle T}$ ${\displaystyle V}$

${\displaystyle T\left(\sum _{\alpha \in A}f_{\alpha }\mathbf {e} _{\alpha }\right)=\sum _{\alpha \in A}f_{\alpha }T(e_{\alpha })=\sum _{\alpha \in A}f_{\alpha }\theta _{\alpha }.}$

Опять же, сумма конечна, поскольку отлична от нуля только для конечного числа . ${\displaystyle f_{\alpha }}$ ${\displaystyle \alpha }$

Множество может быть отождествлено (по сути, по определению) с прямой суммой бесконечного числа копий (рассматриваемых как одномерное векторное пространство над собой), индексированных , т.е. существуют линейные изоморфизмы ${\displaystyle (F^{A})_{0}}$ ${\displaystyle F}$ ${\displaystyle A}$

${\displaystyle V\cong (F^{A})_{0}\cong \bigoplus _{\alpha \in A}F.}$

С другой стороны, является (опять же по определению) прямым произведением бесконечного числа копий , индексированных , и поэтому идентификация ${\displaystyle F^{A}}$ ${\displaystyle F}$ ${\displaystyle A}$

${\displaystyle V^{*}\cong \left(\bigoplus _{\alpha \in A}F\right)^{*}\cong \prod _{\alpha \in A}F^{*}\cong \prod _{\alpha \in A}F\cong F^{A}}$

является частным случаем общего результата, связывающего прямые суммы ( модулей ) с прямыми произведениями.

Если векторное пространство не является конечномерным, то его (алгебраическое) двойственное пространство всегда имеет большую размерность (как кардинальное число ), чем исходное векторное пространство. Это контрастирует со случаем непрерывного двойственного пространства, обсуждаемым ниже, которое может быть изоморфно исходному векторному пространству, даже если последнее является бесконечномерным.

Доказательство этого неравенства между измерениями вытекает из следующего.

Если - бесконечномерное векторное пространство, то арифметические свойства кардинальных чисел подразумевают, что ${\displaystyle V}$ ${\displaystyle F}$

${\displaystyle \mathrm {dim} (V)=|A|<|F|^{|A|}=|V^{\ast }|=\mathrm {max} (|\mathrm {dim} (V^{\ast })|,|F|),}$

где мощности обозначаются как абсолютные значения . Для доказательства этого достаточно доказать то, что можно сделать с помощью аргумента, аналогичного диагональному аргументу Кантора . ^[9] Точная размерность двойственного множества определяется теоремой Эрдёша–Капланского . ${\displaystyle \mathrm {dim} (V)<\mathrm {dim} (V^{*}),}$ ${\displaystyle |F|\leq |\mathrm {dim} (V^{\ast })|,}$

Билинейные произведения и двойственные пространства

Если V конечномерно, то V изоморфно V ^∗ . Но в общем случае между этими двумя пространствами нет естественного изоморфизма . ^[10] Любая билинейная форма ⟨·,·⟩ на V дает отображение V в его сопряженное пространство посредством

${\displaystyle v\mapsto \langle v,\cdot \rangle }$

где правая часть определяется как функционал на V, переводящий каждый w ∈ V в ⟨ v , w ⟩ . Другими словами, билинейная форма определяет линейное отображение

${\displaystyle \Phi _{\langle \cdot ,\cdot \rangle }:V\to V^{*}}$

определяется

${\displaystyle \left[\Phi _{\langle \cdot ,\cdot \rangle }(v),w\right]=\langle v,w\rangle .}$

Если билинейная форма невырождена , то это изоморфизм на подпространство V ^∗ . Если V конечномерно, то это изоморфизм на все V ^∗ . Обратно, любой изоморфизм из V на подпространство V ^∗ (соответственно, на все V ^∗, если V конечномерно) определяет единственную невырожденную билинейную форму на V следующим образом: ${\displaystyle \Phi }$ ${\displaystyle \langle \cdot ,\cdot \rangle _{\Phi }}$

${\displaystyle \langle v,w\rangle _{\Phi }=(\Phi (v))(w)=[\Phi (v),w].\,}$

Таким образом, существует взаимно однозначное соответствие между изоморфизмами V подпространства (соответственно, всех) V ^∗ и невырожденными билинейными формами на V .

Если векторное пространство V находится над комплексным полем, то иногда более естественно рассматривать полуторалинейные формы вместо билинейных. В этом случае заданная полуторалинейная форма ⟨·,·⟩ определяет изоморфизм V с комплексно сопряженным дуальным пространством

${\displaystyle \Phi _{\langle \cdot ,\cdot \rangle }:V\to {\overline {V^{*}}}.}$

Сопряженное пространство двойственного пространства можно отождествить с множеством всех аддитивных комплекснозначных функционалов f  : V → C таких, что ${\displaystyle {\overline {V^{*}}}}$

${\displaystyle f(\alpha v)={\overline {\alpha }}f(v).}$

Впрыск в двойной-двойной

Существует естественный гомоморфизм из в двойной дуал , определяемый для всех . Другими словами, если — оценочное отображение, определяемое , то определяется как отображение . Это отображение всегда инъективно ; ^{[примечание 3]} и оно всегда является изоморфизмом, если — конечномерно. ^[11] Действительно, изоморфизм конечномерного векторного пространства с его двойным дуал является архетипическим примером естественного изоморфизма . Бесконечномерные гильбертовы пространства не изоморфны своим алгебраическим двойным дуалам, а вместо этого — своим непрерывным двойным дуалам. ${\displaystyle \Psi }$ ${\displaystyle V}$ ${\displaystyle V^{**}=\{\Phi :V^{*}\to F:\Phi \ \mathrm {linear} \}}$ ${\displaystyle (\Psi (v))(\varphi )=\varphi (v)}$ ${\displaystyle v\in V,\varphi \in V^{*}}$ ${\displaystyle \mathrm {ev} _{v}:V^{*}\to F}$ ${\displaystyle \varphi \mapsto \varphi (v)}$ ${\displaystyle \Psi :V\to V^{**}}$ ${\displaystyle v\mapsto \mathrm {ev} _{v}}$ ${\displaystyle \Psi }$ ${\displaystyle V}$

Транспонирование линейной карты

Если f  : V → W — линейное отображение , то транспонированное (или двойственное ) f ^∗  : W ^∗ → V ^∗ определяется как

${\displaystyle f^{*}(\varphi )=\varphi \circ f\,}$

для каждого . Результирующий функционал в называется обратным ходом вдоль . ${\displaystyle \varphi \in W^{*}}$ ${\displaystyle f^{*}(\varphi )}$ ${\displaystyle V^{*}}$ ${\displaystyle \varphi }$ ${\displaystyle f}$

Следующее тождество справедливо для всех и : ${\displaystyle \varphi \in W^{*}}$ ${\displaystyle v\in V}$

${\displaystyle [f^{*}(\varphi ),\,v]=[\varphi ,\,f(v)],}$

где скобка [·,·] слева — это естественное спаривание V с его дуальным пространством, а скобка справа — это естественное спаривание W с его дуальным. Это тождество характеризует транспонирование, ^[12] и формально похоже на определение сопряженного .

Назначение f ↦ f ^∗ производит инъективное линейное отображение между пространством линейных операторов из V в W и пространством линейных операторов из W ^∗ в V ^∗ ; этот гомоморфизм является изоморфизмом тогда и только тогда, когда W конечномерно. Если V = W , то пространство линейных отображений на самом деле является алгеброй относительно композиции отображений , и назначение тогда является антигомоморфизмом алгебр, что означает, что ( fg ) ^∗ = g ^∗ f ^∗ . На языке теории категорий взятие двойственного векторных пространств и транспонирование линейных отображений, следовательно, является контравариантным функтором из категории векторных пространств над F в себя. Можно отождествить ( f ^∗ ) ^∗ с f, используя естественную инъекцию в двойной двойственный.

Если линейное отображение f представлено матрицей A относительно двух баз V и W , то f ^∗ представлено транспонированной матрицей A ^T относительно дуальных баз W ^∗ и V ^∗ , отсюда и название. В качестве альтернативы, поскольку f представлено A, действующим слева на векторы-столбцы, f ^∗ представлено той же матрицей, действующей справа на векторы-строки. Эти точки зрения связаны каноническим внутренним произведением на R ⁿ , которое отождествляет пространство векторов-столбцов с дуальным пространством векторов-строк.

Факторпространства и аннигиляторы

Пусть будет подмножеством . Аннулятор в , обозначенный здесь , представляет собой набор линейных функционалов таких, что для всех . То есть, состоит из всех линейных функционалов таких, что ограничение на обращается в нуль: . В конечномерных векторных пространствах аннулятор является двойственным (изоморфным) ортогональному дополнению . ${\displaystyle S}$ ${\displaystyle V}$ ${\displaystyle S}$ ${\displaystyle V^{*}}$ ${\displaystyle S^{0}}$ ${\displaystyle f\in V^{*}}$ ${\displaystyle [f,s]=0}$ ${\displaystyle s\in S}$ ${\displaystyle S^{0}}$ ${\displaystyle f:V\to F}$ ${\displaystyle S}$ ${\displaystyle f|_{S}=0}$

Аннулятор подмножества сам по себе является векторным пространством. Аннулятор нулевого вектора — это все дуальное пространство: , а аннулятор всего пространства — это просто нулевой ковектор: . Более того, назначение аннулятора подмножеству обращает включения, так что если , то ${\displaystyle \{0\}^{0}=V^{*}}$ ${\displaystyle V^{0}=\{0\}\subseteq V^{*}}$ ${\displaystyle V}$ ${\displaystyle \{0\}\subseteq S\subseteq T\subseteq V}$

${\displaystyle \{0\}\subseteq T^{0}\subseteq S^{0}\subseteq V^{*}.}$

Если и являются двумя подмножествами, то ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V}$

${\displaystyle A^{0}+B^{0}\subseteq (A\cap B)^{0}.}$

Если — это любое семейство подмножеств, индексированное по принадлежности некоторому индексному множеству , то ${\displaystyle (A_{i})_{i\in I}}$ ${\displaystyle V}$ ${\displaystyle i}$ ${\displaystyle I}$

${\displaystyle \left(\bigcup _{i\in I}A_{i}\right)^{0}=\bigcap _{i\in I}A_{i}^{0}.}$

В частности, если и являются подпространствами, то ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V}$

${\displaystyle (A+B)^{0}=A^{0}\cap B^{0}}$

и ^{[прим. 3]}

${\displaystyle (A\cap B)^{0}=A^{0}+B^{0}.}$

Если конечномерно и является векторным подпространством , то ${\displaystyle V}$ ${\displaystyle W}$

${\displaystyle W^{00}=W}$

после отождествления со своим образом во втором дуальном пространстве при изоморфизме двойной дуальности . В частности, формирование аннулятора является связностью Галуа на решетке подмножеств конечномерного векторного пространства. ${\displaystyle W}$ ${\displaystyle V\approx V^{**}}$

Если является подпространством , то факторпространство является векторным пространством само по себе, и поэтому имеет двойственное. По первой теореме об изоморфизме функционал пропускается через тогда и только тогда, когда находится в ядре . Таким образом, существует изоморфизм ${\displaystyle W}$ ${\displaystyle V}$ ${\displaystyle V/W}$ ${\displaystyle f:V\to F}$ ${\displaystyle V/W}$ ${\displaystyle W}$ ${\displaystyle f}$

${\displaystyle (V/W)^{*}\cong W^{0}.}$

Как частное следствие, если является прямой суммой двух подпространств и , то является прямой суммой и . ${\displaystyle V}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle V^{*}}$ ${\displaystyle A^{0}}$ ${\displaystyle B^{0}}$

Анализ размеров

Двойственное пространство аналогично "отрицательному"-мерному пространству. Проще говоря, поскольку вектор может быть спарен с ковектором с помощью естественного спаривания для получения скаляра, ковектор может "отменить" размерность вектора, аналогично сокращению дроби . Таким образом, в то время как прямая сумма является ⁠ ⁠ -мерным пространством (если ⁠ ⁠ является ⁠ ⁠ -мерным), ⁠ ⁠ ведет себя как ⁠ ⁠ -мерное пространство, в том смысле, что его размерности могут быть сокращены относительно размерностей ⁠ ⁠ . Это формализуется тензорной контракцией . ${\displaystyle v\in V}$ ${\displaystyle \varphi \in V^{*}}$ ${\displaystyle \langle x,\varphi \rangle :=\varphi (x)\in F}$ ${\displaystyle V\oplus V^{*}}$ ${\displaystyle 2n}$ ${\displaystyle V}$ ${\displaystyle n}$ ${\displaystyle V^{*}}$ ${\displaystyle (-n)}$ ${\displaystyle V}$

Это возникает в физике через размерный анализ , где дуальное пространство имеет обратные единицы. ^[13] При естественном спаривании эти единицы сокращаются, и результирующее скалярное значение является безразмерным , как и ожидалось. Например, в (непрерывном) анализе Фурье или, более широко, частотно-временном анализе : ^{[nb 4]} учитывая одномерное векторное пространство с единицей времени ⁠ ⁠ ${\displaystyle t}$ , дуальное пространство имеет единицы частоты : появления в единицу времени (единицы ⁠ ⁠ ${\displaystyle 1/t}$ ). Например, если время измеряется в секундах , соответствующая дуальная единица — это обратная секунда : в течение 3 секунд событие, которое происходит 2 раза в секунду, происходит в общей сложности 6 раз, что соответствует . Аналогично, если первичное пространство измеряет длину, дуальное пространство измеряет обратную длину . ${\displaystyle 3s\cdot 2s^{-1}=6}$

Непрерывное двойное пространство

При работе с топологическими векторными пространствами непрерывные линейные функционалы из пространства в базовое поле (или ) особенно важны. Это приводит к понятию «непрерывного сопряженного пространства» или «топологического сопряженного», которое является линейным подпространством алгебраического сопряженного пространства , обозначаемым . Для любого конечномерного нормированного векторного пространства или топологического векторного пространства, такого как евклидово n- пространство , непрерывное сопряженное и алгебраическое сопряженное совпадают. Однако это неверно для любого бесконечномерного нормированного пространства, как показано на примере разрывных линейных отображений . Тем не менее, в теории топологических векторных пространств термины «непрерывное сопряженное пространство» и «топологическое сопряженное пространство» часто заменяются на «сопряженное пространство». ${\displaystyle \mathbb {F} =\mathbb {C} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle V^{*}}$ ${\displaystyle V'}$

Для топологического векторного пространства его непрерывное сопряженное пространство , ^[14] или топологическое сопряженное пространство , ^[15] или просто сопряженное пространство ^{[14] [15] [16] [17]} (в смысле теории топологических векторных пространств) определяется как пространство всех непрерывных линейных функционалов . ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle \varphi :V\to {\mathbb {F} }}$

Важными примерами непрерывных двойственных пространств являются пространство финитных основных функций и его двойственное пространство произвольных распределений (обобщенных функций); пространство произвольных основных функций и его двойственное пространство финитных распределений; и пространство быстро убывающих основных функций пространство Шварца и его двойственное пространство умеренных распределений (медленно растущих распределений) в теории обобщенных функций . ${\displaystyle {\mathcal {D}}}$ ${\displaystyle {\mathcal {D}}',}$ ${\displaystyle {\mathcal {E}}}$ ${\displaystyle {\mathcal {E}}',}$ ${\displaystyle {\mathcal {S}},}$ ${\displaystyle {\mathcal {S}}',}$

Характеристики

Если X является хаусдорфовым топологическим векторным пространством ( TVS ) , то непрерывное сопряженное пространство X идентично непрерывному сопряженному пространству пополнения X. [ ^1]

Топологии на двойственной

Существует стандартная конструкция для введения топологии на непрерывном сопряженном топологическом векторном пространстве . Зафиксируем набор ограниченных подмножеств . Это дает топологию на равномерной сходимости на множествах из или, что то же самое, топологию, порожденную полунормами вида ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}},}$

${\displaystyle \|\varphi \|_{A}=\sup _{x\in A}|\varphi (x)|,}$

где — непрерывный линейный функционал на , и пробегает класс ${\displaystyle \varphi }$ ${\displaystyle V}$ ${\displaystyle A}$ ${\displaystyle {\mathcal {A}}.}$

Это означает, что сеть функционалов стремится к функционалу тогда и только тогда, когда ${\displaystyle \varphi _{i}}$ ${\displaystyle \varphi }$ ${\displaystyle V'}$

${\displaystyle {\text{ for all }}A\in {\mathcal {A}}\qquad \|\varphi _{i}-\varphi \|_{A}=\sup _{x\in A}|\varphi _{i}(x)-\varphi (x)|{\underset {i\to \infty }{\longrightarrow }}0.}$

Обычно (но не обязательно) предполагается, что класс удовлетворяет следующим условиям: ${\displaystyle {\mathcal {A}}}$

• Каждая точка принадлежит некоторому множеству : ${\displaystyle x}$ ${\displaystyle V}$ ${\displaystyle A\in {\mathcal {A}}}$

  ${\displaystyle {\text{ for all }}x\in V\quad {\text{ there exists some }}A\in {\mathcal {A}}\quad {\text{ such that }}x\in A.}$

• Каждые два множества и содержатся в некотором множестве : ${\displaystyle A\in {\mathcal {A}}}$ ${\displaystyle B\in {\mathcal {A}}}$ ${\displaystyle C\in {\mathcal {A}}}$

  ${\displaystyle {\text{ for all }}A,B\in {\mathcal {A}}\quad {\text{ there exists some }}C\in {\mathcal {A}}\quad {\text{ such that }}A\cup B\subseteq C.}$

• ${\displaystyle {\mathcal {A}}}$замкнуто относительно операции умножения на скаляры:

  ${\displaystyle {\text{ for all }}A\in {\mathcal {A}}\quad {\text{ and all }}\lambda \in {\mathbb {F} }\quad {\text{ such that }}\lambda \cdot A\in {\mathcal {A}}.}$

Если эти требования выполнены, то соответствующая топология на является хаусдорфовой и множества ${\displaystyle V'}$

${\displaystyle U_{A}~=~\left\{\varphi \in V'~:~\quad \|\varphi \|_{A}<1\right\},\qquad {\text{ for }}A\in {\mathcal {A}}}$

формируют его местную базу.

Вот три наиболее важных особых случая.

• Сильная топология на — это топология равномерной сходимости на ограниченных подмножествах в (поэтому здесь можно выбрать класс всех ограниченных подмножеств в ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$

Если — нормированное векторное пространство (например, банахово или гильбертово ), то сильная топология на является нормированной (фактически банаховым пространством, если поле скаляров является полным), с нормой ${\displaystyle V}$ ${\displaystyle V'}$

${\displaystyle \|\varphi \|=\sup _{\|x\|\leq 1}|\varphi (x)|.}$

• Стереотипная топология на — это топология равномерной сходимости на вполне ограниченных множествах в (поэтому здесь можно выбрать класс всех вполне ограниченных подмножеств в ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$
• Слабая топология на — это топология равномерной сходимости на конечных подмножествах в (поэтому здесь можно выбрать класс всех конечных подмножеств в ). ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle {\mathcal {A}}}$ ${\displaystyle V}$

Каждый из этих трех вариантов топологии приводит к варианту свойства рефлексивности для топологических векторных пространств: ${\displaystyle V'}$

• Если наделено сильной топологией , то соответствующее понятие рефлексивности является стандартным: пространства, рефлексивные в этом смысле, просто называются рефлексивными . ^[18] ${\displaystyle V'}$
• Если наделено стереотипной двойственной топологией, то соответствующая рефлексивность представлена ​​в теории стереотипных пространств : рефлексивные в этом смысле пространства называются стереотипными . ${\displaystyle V'}$
• Если наделено слабой топологией , то соответствующая рефлексивность представлена ​​в теории дуальных пар : ^[19] рефлексивные в этом смысле пространства являются произвольными (хаусдорфовыми) локально выпуклыми пространствами со слабой топологией. ^[20] ${\displaystyle V'}$

Примеры

Пусть 1 < p < ∞ — действительное число и рассмотрим банахово пространство ℓ  p всех последовательностей a = ( a _n ), для которых

${\displaystyle \|\mathbf {a} \|_{p}=\left(\sum _{n=0}^{\infty }|a_{n}|^{p}\right)^{\frac {1}{p}}<\infty .}$

Определим число q как 1/ p + 1/ q = 1. Тогда непрерывный двойственный элемент ℓ ^p естественным образом отождествляется с ℓ ^q : задан элемент , соответствующий элемент ℓ ^q является последовательностью , где обозначает последовательность, n -й член которой равен 1, а все остальные равны нулю. Наоборот, задан элемент a = ( a _n ) ∈ ℓ ^q , соответствующий непрерывный линейный функционал на ℓ ^p определяется как ${\displaystyle \varphi \in (\ell ^{p})'}$ ${\displaystyle (\varphi (\mathbf {e} _{n}))}$ ${\displaystyle \mathbf {e} _{n}}$ ${\displaystyle \varphi }$

${\displaystyle \varphi (\mathbf {b} )=\sum _{n}a_{n}b_{n}}$

для всех b = ( b _n ) ∈ ℓ ^p (см. неравенство Гёльдера ).

Аналогичным образом, непрерывное сопряженное пространство ℓ ¹ естественным образом отождествляется с ℓ ^∞ (пространством ограниченных последовательностей). Более того, непрерывные сопряженные пространства банаховых пространств c (состоящие из всех сходящихся последовательностей с супремум-нормой ) и c ₀ (последовательности, сходящиеся к нулю) естественным образом отождествляются с ℓ ¹ .

По теореме Рисса о представлении непрерывное сопряженное пространство гильберта снова является гильбертовым пространством, которое антиизоморфно исходному пространству. Это приводит к обозначению скобок, используемому физиками в математической формулировке квантовой механики .

По теореме Рисса–Маркова–Какутани о представлении непрерывное сопряженное пространство некоторых пространств непрерывных функций можно описать с помощью мер.

Транспонирование непрерывного линейного отображения

Если T  : V → W — непрерывное линейное отображение между двумя топологическими векторными пространствами, то (непрерывное) транспонирование T′  : W′ → V′ определяется той же формулой, что и раньше:

${\displaystyle T'(\varphi )=\varphi \circ T,\quad \varphi \in W'.}$

Результирующий функционал T′ ( φ ) находится в V′ . Назначение T → T′ создает линейное отображение между пространством непрерывных линейных отображений из V в W и пространством линейных отображений из W′ в V′ . Когда T и U являются составными непрерывными линейными отображениями, то

${\displaystyle (U\circ T)'=T'\circ U'.}$

Когда V и W — нормированные пространства, норма транспонирования в L ( W′ , V′ ) равна норме T в L ( V , W ) . Несколько свойств транспонирования зависят от теоремы Хана–Банаха . Например, ограниченное линейное отображение T имеет плотный диапазон тогда и только тогда, когда транспонирование T′ инъективно.

Когда T — компактное линейное отображение между двумя банаховыми пространствами V и W , то транспонированное T′ компактно. Это можно доказать с помощью теоремы Арцела–Асколи .

Когда V — гильбертово пространство, существует антилинейный изоморфизм i _V из V на его непрерывное сопряженное V′ . Для любого ограниченного линейного отображения T на V транспонированный и сопряженный операторы связаны соотношением

${\displaystyle i_{V}\circ T^{*}=T'\circ i_{V}.}$

Когда T — непрерывное линейное отображение между двумя топологическими векторными пространствами V и W , то транспонирование T′ непрерывно, когда W′ и V′ снабжены «совместимыми» топологиями: например, когда для X = V и X = W , оба дуала X′ имеют сильную топологию β ( X′ , X ) равномерной сходимости на ограниченных множествах X , или оба имеют слабую-∗ топологию σ ( X′ , X ) поточечной сходимости на  X . Транспонирование T′ непрерывно от β ( W′ , W ) до β ( V′ , V ) или от σ ( W′ , W ) до σ ( V′ , V ) .

Аннигиляторы

Предположим, что W — замкнутое линейное подпространство нормированного пространства  V , и рассмотрим аннулятор W в V′ ,

${\displaystyle W^{\perp }=\{\varphi \in V':W\subseteq \ker \varphi \}.}$

Тогда, двойственное к фактору V  /  W  можно отождествить с W ^⊥ , а двойственное к W можно отождествить с фактором V′  /  W ^⊥ . ^[21] Действительно, пусть P обозначает каноническую сюръекцию из V на фактор V  /  W  ; тогда транспонирование P′ является изометрическим изоморфизмом из ( V  /  W  )′ в V′ с областью действия, равной W ^⊥ . Если j обозначает отображение инъекции из W в V , то ядро ​​транспонирования j′ является аннулятором W :

${\displaystyle \ker(j')=W^{\perp }}$

и из теоремы Хана–Банаха следует , что j′ индуцирует изометрический изоморфизм V′  /  W ^⊥ → W′ .

Дополнительные свойства

Если двойственное к нормированному пространству V сепарабельно , то и само пространство V сепарабельно . Обратное неверно: например, пространство ℓ ¹ сепарабельно, а его двойственное ℓ ^∞ — нет.

Двойной двойной

Это естественное преобразование векторного сложения из векторного пространства в его двойное дуальное. ⟨ x ₁ , x ₂ ⟩ обозначает упорядоченную пару из двух векторов. Сложение + переводит x ₁ и x ₂ в x ₁ + x ₂ . Сложение +′, вызванное преобразованием, можно определить как для любого в дуальном пространстве. ${\displaystyle [\Psi (x_{1})+'\Psi (x_{2})](\varphi )=\varphi (x_{1}+x_{2})=\varphi (x)}$ ${\displaystyle \varphi }$

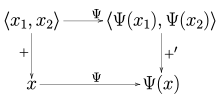
По аналогии со случаем алгебраического двойного дуала всегда существует естественно определенный непрерывный линейный оператор Ψ : V → V′′ из нормированного пространства V в его непрерывный двойной дуал V′′ , определяемый соотношением

${\displaystyle \Psi (x)(\varphi )=\varphi (x),\quad x\in V,\ \varphi \in V'.}$

Как следствие теоремы Хана–Банаха , это отображение фактически является изометрией , то есть ‖ Ψ( x ) ‖ = ‖ x ‖ для всех x ∈ V. Нормированные пространства, для которых отображение Ψ является биекцией , называются рефлексивными .

Когда V является топологическим векторным пространством , то Ψ( x ) по-прежнему может быть определено той же формулой для каждого x ∈ V , однако возникает несколько трудностей. Во-первых, когда V не является локально выпуклым , непрерывное сопряженное может быть равно { 0 }, а отображение Ψ тривиальным. Однако, если V является хаусдорфовым и локально выпуклым, отображение Ψ инъективно из V в алгебраическое сопряженное V′ ^∗ непрерывного сопряженного, снова как следствие теоремы Хана–Банаха. ^{[nb 5]}

Во-вторых, даже в локально выпуклой обстановке несколько естественных топологий векторного пространства могут быть определены на непрерывном дуальном V′ , так что непрерывное двойное дуальное V′′ не определяется однозначно как множество. Утверждение, что Ψ отображает из V в V′′ , или, другими словами, что Ψ( x ) непрерывно на V′ для каждого x ∈ V , является разумным минимальным требованием к топологии V′ , а именно, что отображения оценки

${\displaystyle \varphi \in V'\mapsto \varphi (x),\quad x\in V,}$

быть непрерывным для выбранной топологии на V′ . Кроме того, все еще существует выбор топологии на V′′ , и непрерывность Ψ зависит от этого выбора. Как следствие, определение рефлексивности в этом каркасе более сложно, чем в нормированном случае.

Смотрите также

• Ковариантность и контравариантность векторов
• Двойной модуль
• Двойная норма
• Двойственность (математика)
• Двойственность (проективная геометрия)
• Двойственность Понтрягина
• Обратная решетка – базис двойного пространства, в кристаллографии

Примечания

1. Для использования в этом смысле см. An Introduction to Manifolds (Tu 2011, стр. 19). Это обозначение иногда используется, когда зарезервировано для какого-то другого значения. Например, в приведенном выше тексте часто используется для обозначения кодифференциала , так что представляет собой обратный образ формы . Халмош (1974, стр. 20) использует для обозначения алгебраического двойственного к . Однако другие авторы используют для непрерывного двойственного, резервируя для алгебраического двойственного (Trèves 2006, стр. 35). ${\displaystyle V^{\lor }}$ ${\displaystyle (\cdot )^{*}}$ ${\displaystyle F^{*}}$ ${\displaystyle F}$ ${\displaystyle F^{*}\omega }$ ${\displaystyle \omega }$ ${\displaystyle V'}$ ${\displaystyle V}$ ${\displaystyle V'}$ ${\displaystyle V^{*}}$
2. Во многих областях, таких как квантовая механика , ⟨·,·⟩ зарезервировано для полуторалинейной формы, определенной на V × V .
3. Несколько утверждений в этой статье требуют аксиомы выбора для своего обоснования. Аксиома выбора нужна, чтобы показать, что произвольное векторное пространство имеет базис: в частности, она нужна, чтобы показать, что имеет базис. Она также нужна, чтобы показать, что двойственное к бесконечномерному векторному пространству ненулевое, и, следовательно, что естественное отображение из в его двойной двойственный является инъективным. ${\displaystyle \mathbb {R} ^{\mathbb {N} }}$ ${\displaystyle V}$ ${\displaystyle V}$
4. Если быть точным, непрерывный анализ Фурье изучает пространство функционалов с областью определения векторное пространство и пространство функционалов на двойственном векторном пространстве.
5. Если V локально выпукло, но не хаусдорфово, ядро ​​Ψ является наименьшим замкнутым подпространством, содержащим {0}.

Ссылки

1. Narici & Beckenstein 2011, стр. 225–273.
2. Кацнельсон и Кацнельсон (2008), с. 37, §2.1.3
3. Tu (2011) стр. 19, §3.1
4. Акслер (2015) стр. 101, §3.94
5. Халмош (1974) стр. 20, §13
6. Халмош (1974) стр. 21, §14
7. Мизнер, Торн и Уилер 1973
8. Мизнер, Торн и Уилер 1973, §2.5
9. Николя Бурбаки (1974). Герман (ред.). Элементы математики: Алгебра I, Главы 1 - 3. С. 400. ISBN 0201006391.
10. Маклейн и Биркгофф 1999, §VI.4
11. Халмош (1974) стр. 25, 28
12. Халмош (1974) §44
13. Тао, Теренс (29.12.2012). "Математическая формализация размерного анализа". Аналогично можно определить как двойственное пространство к ... ${\displaystyle V^{T^{-1}}}$ ${\displaystyle V^{T}}$
14. Робертсон и Робертсон 1964, II.2
15. Шефер 1966, II.4
16. Рудин 1973, 3.1
17. Бурбаки 2003, II.42
18. Шефер 1966, IV.5.5
19. Шефер 1966, IV.1
20. Шефер 1966, IV.1.2
21. Рудин 1991, глава 4

Библиография

• Акслер, Шелдон Джей (2015). Линейная алгебра, сделанная правильно (3-е изд.). Springer . ISBN 978-3-319-11079-0.
• Бурбаки, Николя (1989). Элементы математики, Алгебра I. Springer-Verlag. ISBN 3-540-64243-9.
• Бурбаки, Николя (2003). Элементы математики, Топологические векторные пространства . Springer-Verlag.
• Халмош, Пол Ричард (1974) [1958]. Конечномерные векторные пространства (2-е изд.). Springer . ISBN 0-387-90093-4.
• Кацнельсон, Ицхак ; Кацнельсон, Йонатан Р. (2008). (Краткое) Введение в линейную алгебру . Американское математическое общество . ISBN 978-0-8218-4419-9.
• Ланг, Серж (2002), Алгебра , Graduate Texts in Mathematics , т. 211 (пересмотренное третье издание), Нью-Йорк: Springer-Verlag, ISBN 978-0-387-95385-4, MR  1878556, Zbl  0984.00001
• Ту, Лоринг В. (2011). Введение в многообразия (2-е изд.). Springer . ISBN 978-1-4419-7400-6.
• Mac Lane, Saunders ; Birkhoff, Garrett (1999). Алгебра (3-е изд.). AMS Chelsea Publishing. ISBN 0-8218-1646-2..
• Мизнер, Чарльз В.; Торн , Кип С.; Уилер , Джон А. (1973). Гравитация . WH Freeman. ISBN 0-7167-0344-0.
• Наричи, Лоуренс; Бекенштейн, Эдвард (2011). Топологические векторные пространства . Чистая и прикладная математика (Второе изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1584888666. OCLC  144216834.
• Рудин, Уолтер (1973). Функциональный анализ . Международная серия по чистой и прикладной математике. Том 25 (первое издание). Нью-Йорк, Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN 9780070542259.
• Рудин, Уолтер (1991). Функциональный анализ. Международная серия по чистой и прикладной математике. Том 8 (Второе издание). Нью-Йорк, Нью-Йорк: McGraw-Hill Science/Engineering/Math . ISBN 978-0-07-054236-5. OCLC  21163277.
• Робертсон, А. П.; Робертсон, У. (1964). Топологические векторные пространства . Cambridge University Press.
• Шефер, Хельмут Х. (1966). Топологические векторные пространства . Нью-Йорк: The Macmillan Company.
• Шефер, Хельмут Х.; Вольф, Манфред П. (1999). Топологические векторные пространства . GTM . Том 8 (Второе издание). Нью-Йорк, Нью-Йорк: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135.
• Тревес, Франсуа (2006) [1967]. Топологические векторные пространства, распределения и ядра . Минеола, Нью-Йорк: Dover Publications. ISBN 978-0-486-45352-1. OCLC  853623322.

Внешние ссылки

• Вайсштейн, Эрик В. «Двойственное векторное пространство». MathWorld .